河北省中考数学压轴题汇总

河北省中考数学压轴题汇总

‎2010/26．（本小题满分12分）‎ 某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y =x＋150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）（利润 = 销售额－成本－广告费）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳x2 元的附加费，设月利润为w外（元）（利润 = 销售额－成本－附加费）．‎ ‎（1）当x = 1000时，y = 元/件，w内 = 元；‎ ‎（2）分别求出w内，w外与x间的函数关系式（不必写x的取值范围）；‎ ‎（3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内 销售月利润的最大值相同，求a的值；‎ （4） 如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还 是在国外销售才能使所获月利润较大？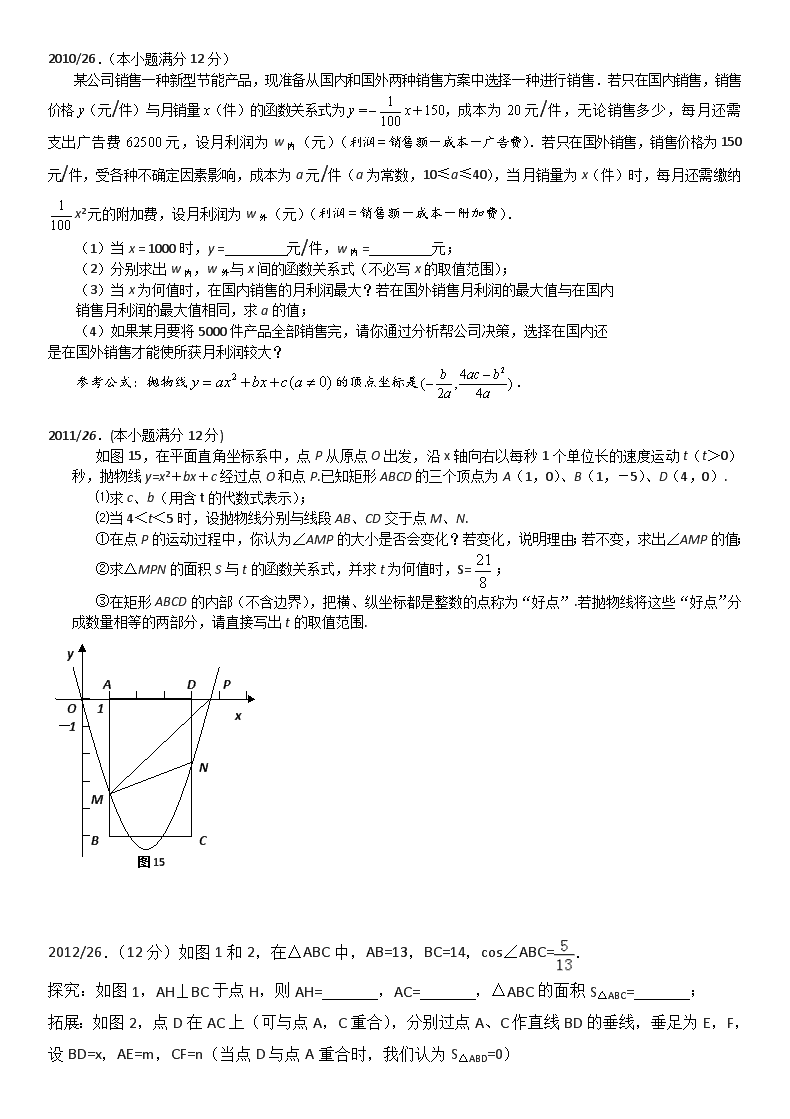‎ 参考公式：抛物线的顶点坐标是．‎ ‎2011/26．(本小题满分12分)‎ 如图15，在平面直角坐标系中，点P从原点O出发，沿x轴向右以每秒1个单位长的速度运动t（t＞0）秒，抛物线y=x2＋bx＋c经过点O和点P.已知矩形ABCD的三个顶点为A（1，0）、B（1，－5）、D（4，0）.‎ ‎⑴求c、b（用含t的代数式表示）；‎ ‎⑵当4＜t＜5时，设抛物线分别与线段AB、CD交于点M、N.‎ ‎①在点P的运动过程中，你认为∠AMP的大小是否会变化？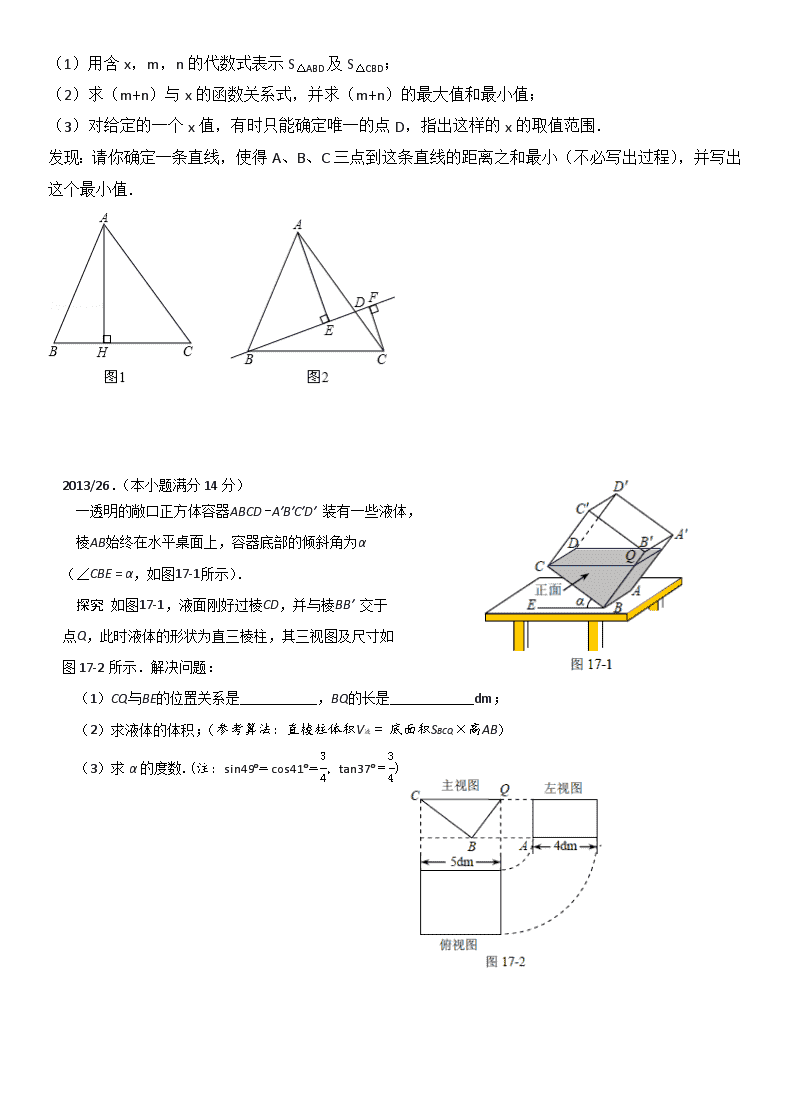若变化，说明理由；若不变，求出∠AMP的值；‎ ‎②求△MPN的面积S与t的函数关系式，并求t为何值时，S=；‎ ‎③在矩形ABCD的内部（不含边界），把横、纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围.‎ A D P O ‎－1‎ M N C B x y ‎1‎ 图15‎ ‎2012/26．（12分）如图1和2，在△ABC中，AB=13，BC=14，cos∠ABC=．‎ 探究：如图1，AH⊥BC于点H，则AH=　 　，AC=　 　，△ABC的面积S△ABC=　 　；‎ 拓展：如图2，点D在AC上（可与点A，C重合），分别过点A、C作直线BD的垂线，垂足为E，F，设BD=x，AE=m，CF=n（当点D与点A重合时，我们认为S△ABD=0）‎ ‎（1）用含x，m，n的代数式表示S△ABD及S△CBD；‎ ‎（2）求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；‎ ‎（3）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围．‎ 发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值．‎ ‎2013/26．（本小题满分14分）‎ 一透明的敞口正方体容器ABCD -A′B′C′D′ 装有一些液体，‎ 棱AB始终在水平桌面上，容器底部的倾斜角为α ‎ ‎（∠CBE = α，如图17-1所示）．‎ 探究 如图17-1，液面刚好过棱CD，并与棱BB′ 交于 ‎ 点Q，此时液体的形状为直三棱柱，其三视图及尺寸如 ‎ 图17-2所示．解决问题：‎ ‎（1）CQ与BE的位置关系是___________，BQ的长是____________dm； ‎ ‎（2）求液体的体积；（参考算法：直棱柱体积V液 = 底面积SBCQ×高AB） ‎ ‎（3）求α的度数.(注：sin49°＝cos41°＝，tan37°＝)‎ 拓展 在图17-1的基础上，以棱AB为轴将容器向左或向右旋转，但不能使液体溢出，图17-3或图17-4是其正面示意图.若液面与棱C′C或CB交于点P，设PC = x，BQ = y.分别就图17-3和图17-4求y与x的函数关系式，并写出相应的α的范围.‎ 延伸 在图17-4的基础上，于容器底部正中间位置，嵌入一平行于侧面的长方形隔板（厚度忽略不计），得到图17-5，隔板高NM = 1 dm，BM = CM，NM⊥BC.继续向右缓慢旋转，当α = 60°时，通过计算，判断溢出容器的液体能否达到4 dm3.‎ ‎2014/26（本小题满分13分）‎ A(出口)‎ C(景点)‎ D B ‎1号车 ‎2号车 K(甲)‎ 图16-1‎ A(出口)‎ C(景点)‎ D B ‎1号车 ‎2号车 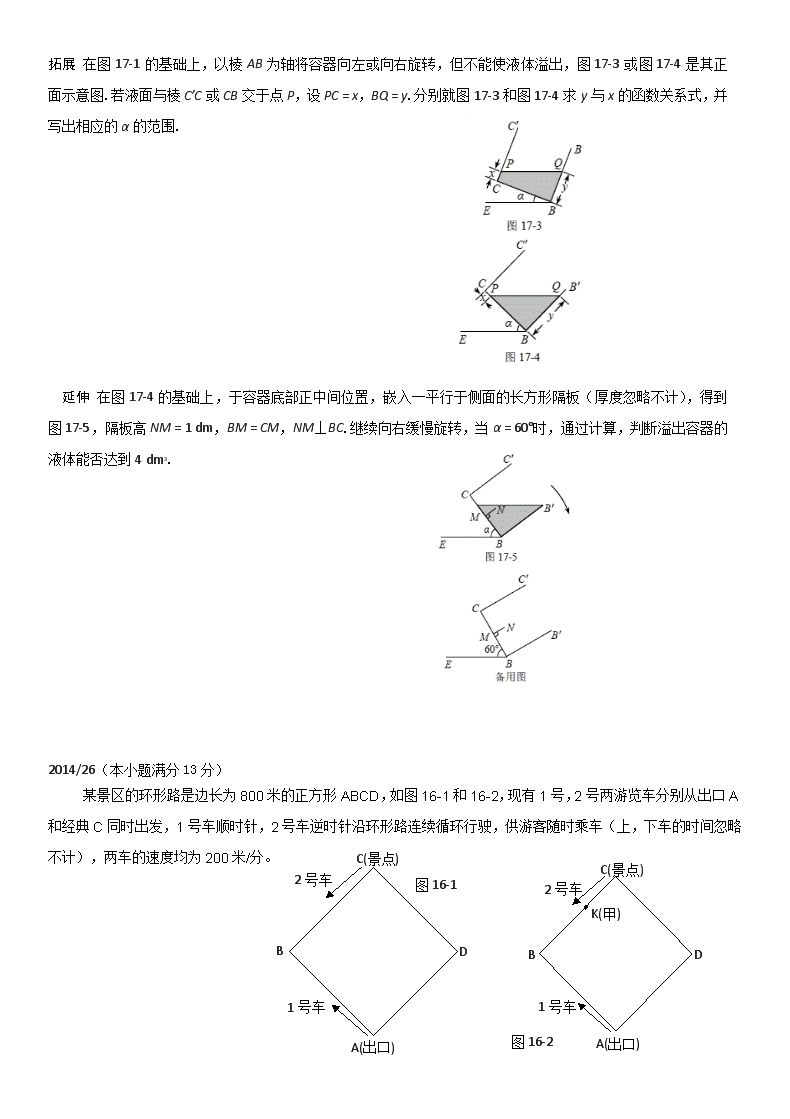某景区的环形路是边长为800米的正方形ABCD，如图16-1和16-2，现有1号，2号两游览车分别从出口A和经典C同时出发，1号车顺时针，2号车逆时针沿环形路连续循环行驶，供游客随时乘车（上，下车的时间忽略不计），两车的速度均为200米/分。‎ 图16-2‎ 探究：设行驶时间为t分 ‎（1）当0≤t≤s时，分别写出1号车，2号车在左半环线离出口A的路程y1，y2（米）与t（分）的函数关系式，并求出当两车相距的路程是400米时t的值；‎ ‎（2）t为何值时，1号车第三次恰好经过点C？，并直接写出这一段时间内它与2号车 相遇过的次数。‎ 发现 如图16-2，游客甲在BC上一点K（不与点B，C重合）处候车，准备乘车到出口A，设CK=x米。‎ 情况一：若他刚好错过2号车，便搭乘即将到来的1号车；‎ 情况二：若他刚好错过1号车，便搭乘即将到来的2号车；‎ 比较哪种情况用时较多？（含候车时间）‎ 决策 已知游客乙在DA上从D向出口A走去，步行的速度是50米/分，当行进到DA上一点P（不与D,A重合）时，刚好与2号车相遇。‎ ‎（1）他发现，乘1号车会比乘2号车到出口A用时少，请你简要说明理由；‎ ‎（2）设PA=s（00)，用含x的代数式表示BN的长，并求x的取值范围.‎ 探究：当半圆K与矩形ABCD的边相切时，求sin的值.‎ 备用图 ‎2016/26.(本小题满分12分)‎ ‎ 如图12.抛物线L：(常数t>0)与x轴从左到右的交点为B.A.过线段OA的中点M作MP⊥x轴.交双曲线(k>0.x>0)于点P.且OA·MP=12‎ ‎ ⑴求k值；‎ ‎ ⑵当t=1时.求AB长.并求直线MP与L对称轴之间的距离；‎ ‎ ⑶把L在直线MP左侧部分的图象(含与直线MP的交点)记为G.用t表示图象G最高点的坐标；‎ ‎ ⑷设L与双曲线有个交点的横坐标为.且满足.通过L位置随t变化的过程.直接写出t的取值范围 图12‎ ‎ ‎ ‎2017/26．（12分）某厂按用户的月需求量x（件）完成一种产品的生产，其中x＞0，每件的售价为18万元，每件的成本y（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x（件）成反比，经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12），符合关系式x＝2n2﹣2kn＋9（k＋3）（k为常数），且得到了表中的数据．‎ 月份n（月）‎ ‎1‎ ‎2‎ 成本y（万元/件）‎ ‎11‎ ‎12‎ 需求量x（件/月）‎ ‎120‎ ‎100‎ ‎（1）求y与x满足的关系式，请说明一件产品的利润能否是12万元；‎ ‎（2）求k，并推断是否存在某个月既无盈利也不亏损；‎ ‎（3）在这一年12个月中，若第m个月和第（m＋1）个月的利润相差很大，求m．‎ ‎2018/26．（11.00分）（2018•河北）如图是轮滑场地的截面示意图，平台AB距x轴（水平）18米，与y轴交于点B，与滑道y=（x≥1）交于点A，且AB=1米．运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落路线的某位置．忽略空气阻力，实验表明：M，A的竖直距离h（米）与飞出时间t（秒）的平方成正比，且t=1时h=5，M，A的水平距离是vt米．‎ ‎（1）求k，并用t表示h；‎ ‎（2）设v=5．用t表示点M的横坐标x和纵坐标y，并求y与x的关系式（不写x的取值范围），及y=13时运动员与正下方滑道的竖直距离；‎ ‎（3）若运动员甲、乙同时从A处飞出，速度分别是5米/秒、v乙米/秒．当甲距x轴1.8米，且乙位于甲右侧超过4.5米的位置时，直接写出t的值及v乙的范围．‎ ‎2019/26．（12分）如图，若b是正数，直线l：y＝b与y轴交于点A；直线a：y＝x﹣b与y轴交于点B；抛物线L：y＝﹣x2+bx的顶点为C，且L与x轴右交点为D．‎ ‎（1）若AB＝8，求b的值，并求此时L的对称轴与a的交点坐标；‎ ‎（2）当点C在l下方时，求点C与l距离的最大值；‎ ‎（3）设x0≠0，点（x0，y1），（x0，y2），（x0，y3）分别在l，a和L上，且y3是y1，y2的平均数，求点（x0，0）与点D间的距离；‎ ‎（4）在L和a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b＝2019和b＝2019.5时“美点”的个数．‎ 答 案 ‎2010/26．解：（1）140 57500；‎ ‎（2）w内 = x（y -20）- 62500 = x2＋130 x，‎ w外 = x2＋（150）x．‎ ‎（3）当x = = 6500时，w内最大；分 由题意得 ， ‎ 解得a1 = 30，a2 = 270（不合题意，舍去）．所以 a = 30． ‎ ‎（4）当x  = 5000时，w内 = 337500， w外 =．‎ 若w内 ＜ w外，则a＜32.5；‎ 若w内 = w外，则a = 32.5；‎ 若w内 ＞ w外，则a＞32.5．‎ 所以，当10≤ a ＜32.5时，选择在国外销售；‎ 当a = 32.5时，在国外和国内销售都一样；‎ 当32.5＜ a ≤40时，选择在国内销售．‎ ‎（2011•河北）26、如图，在平面直角坐标系中，点P从原点O出发，沿x轴向右以毎秒1个单位长的速度运动t秒（t＞0），抛物线y=x2+bx+c经过点O和点P，已知矩形ABCD的三个顶点 为 A （1，0），B （1，﹣5），D （4，0）．‎ ‎（1）求c，b （用含t的代数式表示）：‎ ‎（2）当4＜t＜5时，设抛物线分别与线段AB，CD交于点M，N．‎ ‎①在点P的运动过程中，你认为∠AMP的大小是否会变化？若变化，说明理由；若不变，求出∠AMP的值；‎ ‎②求△MPN的面积S与t的函数关系式，并求t为何值时，；‎ ‎（3）在矩形ABCD的内部（不含边界），把横、纵 ‎ 坐标都是整数的点称为“好点”．若抛物线将这些“好点”分成数量相等的两部分，请直接写出t的取值范围．‎ 考点：二次函数综合题。‎ 分析：（1）由抛物线y=x2+bx+c经过点O和点P，将点O与P的坐标代入方程即可求得c，b；‎ ‎（2）①当x=1时，y=1﹣t，求得M的坐标，则可求得∠AMP的度数，‎ ‎②由S=S四边形AMNP﹣S△PAM=S△DPN+S梯形NDAM﹣S△PAM，即可求得关于t的二次函数，列方程即可求得t的值；‎ ‎（3）根据图形，即可直接求得答案．‎ 解答：解：（1）把x=0，y=0代入y=x2+bx+c，得c=0，‎ 再把x=t，y=0代入y=x2+bx，得t2+bt=0，‎ ‎∵t＞0，‎ ‎∴b=﹣t；‎ ‎（2）①不变．‎ 如图6，当x=1时，y=1﹣t，故M（1，1﹣t），‎ ‎∵tan∠AMP=1，‎ ‎∴∠AMP=45°；‎ ‎②S=S四边形AMNP﹣S△PAM=S△DPN+S梯形NDAM﹣S△PAM=（t﹣4）（4t﹣16）+[（4t﹣16）+（t﹣1）]×3﹣（t﹣1）（t﹣1）=t2﹣t+6．‎ 解t2﹣t+6=，‎ 得：t1=，t2=，‎ ‎∵4＜t＜5，‎ ‎∴t1=舍去，‎ ‎∴t=．‎ ‎（3）＜t＜．‎ 点评：此题考查了二次函数与点的关系，以及三角形面积的求解方法等知识．此题综合性很强，难度适中，解题的关键是注意数形结合与方程思想的应用．‎ ‎　2012/26．（12分）如图1和2，在△ABC中，AB=13，BC=14，cos∠ABC=．‎ 探究：如图1，AH⊥BC于点H，则AH=　12　，AC=　15　，△ABC的面积S△ABC=　84　；‎ 拓展：如图2，点D在AC上（可与点A，C重合），分别过点A、C作直线BD的垂线，垂足为E，F，设BD=x，AE=m，CF=n（当点D与点A重合时，我们认为S△ABD=0）‎ ‎（1）用含x，m，n的代数式表示S△ABD及S△CBD；‎ ‎（2）求（m+n）与x的函数关系式，并求（m+n）的最大值和最小值；‎ ‎（3）对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围．‎ 发现：请你确定一条直线，使得A、B、C三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值．‎ ‎【考点】GB：反比例函数综合题；KQ：勾股定理；T7：解直角三角形．菁优网版权所有 ‎【专题】16：压轴题．‎ ‎【分析】探究：先在直角△ABH中，由AB=13，cos∠ABC=，可得AH=12，BH=5，则CH=9，再解直角△ACH，即可求出AC的值，最后根据三角形的面积公式即可求出S ‎△ABC的值；‎ 拓展：（1）由三角形的面积公式即可求解；‎ ‎（2）首先由（1）可得m=，n=，再根据S△ABD+S△CBD=S△ABC=84，即可求出（m+n）与x的函数关系式，然后由点D在AC上（可与点A，C重合），可知x的最小值为AC边上的高，最大值为BC的长；‎ ‎（3）由于BC＞BA，所以当以B为圆心，以大于且小于13为半径画圆时，与AC有两个交点，不符合题意，故根据点D的唯一性，分两种情况：①当BD为△ABC的边AC上的高时，D点符合题意；②当AB＜BD≤BC时，D点符合题意；‎ 发现：由于AC＞BC＞AB，所以使得A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线．‎ ‎【解答】解：探究：在直角△ABH中，∵∠AHB=90°，AB=13，cos∠ABC=，‎ ‎∴BH=AB•cos∠ABC=5，AH=12，∴CH=BC﹣BH=9．‎ 在△ACH中，∵∠AHC=90°，AH=12，CH=9，∴AC=15，∴S△ABC=BC•AH=×14×12=84．‎ 故答案为12，15，84；‎ 拓展 （1）由三角形的面积公式，得S△ABD=BD•AE=xm，S△CBD=BD•CF=xn；‎ ‎（2）由（1）得m=，n=，‎ ‎∴m+n=+=，‎ ‎∵AC边上的高为==，‎ ‎∴x的取值范围是≤x≤14．‎ ‎∵（m+n）随x的增大而减小，‎ ‎∴当x=时，（m+n）的最大值为15；‎ 当x=14时，（m+n）的最小值为12；‎ ‎（3）x的取值范围是x=或13＜x≤14．‎ 发现：∵AC＞BC＞AB，‎ ‎∴过A、B、C三点到这条直线的距离之和最小的直线就是AC所在的直线，AC边上的高的长为．‎ ‎【点评】本题考查了解直角三角形，勾股定理，三角形的面积，反比例函数的性质等知识，综合性较强，有一定难度．‎ ‎2013/26‎ ‎2014/26‎ ‎2015/26‎ ‎2016/26‎ ‎ ‎ ‎　‎ ‎2017/26‎ ‎2018/26‎ ‎26．（11.00分）（2018•河北）如图是轮滑场地的截面示意图，平台AB距x轴（水平）18米，与y轴交于点B，与滑道y=（x≥1）交于点A，且AB=1米．运动员（看成点）在BA方向获得速度v米/秒后，从A处向右下飞向滑道，点M是下落路线的某位置．忽略空气阻力，实验表明：M，A的竖直距离h（米）与飞出时间t（秒）的平方成正比，且t=1时h=5，M，A的水平距离是vt米．‎ ‎（1）求k，并用t表示h；‎ ‎（2）设v=5．用t表示点M的横坐标x和纵坐标y，并求y与x的关系式（不写x的取值范围），及y=13时运动员与正下方滑道的竖直距离；‎ ‎（3）若运动员甲、乙同时从A处飞出，速度分别是5米/秒、v乙米/秒．当甲距x轴1.8米，且乙位于甲右侧超过4.5米的位置时，直接写出t的值及v乙的范围．‎ ‎【分析】（1）用待定系数法解题即可；‎ ‎（2）根据题意，分别用t表示x、y，再用代入消元法得出y与x之间的关系式；‎ ‎（3）求出甲距x轴1.8米时的横坐标，根据题意求出乙位于甲右侧超过4.5米的v乙．‎ ‎【解答】解：（1）由题意，点A（1，18）带入y=‎ 得：18=‎ ‎∴k=18‎ 设h=at2，把t=1，h=5代入 ‎∴a=5‎ ‎∴h=5t2‎ ‎（2）∵v=5，AB=1‎ ‎∴x=5t+1‎ ‎∵h=5t2，OB=18‎ ‎∴y=﹣5t2+18‎ 由x=5t+1‎ 则t=‎ ‎∴y=﹣‎ 当y=13时，13=﹣‎ 解得x=6或﹣4‎ ‎∵x≥1‎ ‎∴x=6‎ 把x=6代入y=‎ y=3‎ ‎∴运动员在与正下方滑道的竖直距离是13﹣3=10（米）‎ ‎（3）把y=1.8代入y=﹣5t2+18‎ 得t2=‎ 解得t=1.8或﹣1.8（负值舍去）‎ ‎∴x=10‎ ‎∴甲坐标为（10，1.8）恰号落在滑道y=上 此时，乙的坐标为（1+1.8v乙，1.8）‎ 由题意：1+1.8v乙﹣（1+5×1.8）＞4.5‎ ‎∴v乙＞7.5‎ ‎【点评】本题以考查二次函数和反比例函数的待定系数法以及函数图象上的临界点问题 ‎2019/26．【解答】解：（1）当x＝0吋，y＝x﹣b＝﹣b，‎ ‎∴B （0，﹣b），‎ ‎∵AB＝8，而A（0，b），‎ ‎∴b﹣（﹣b）＝8，‎ ‎∴b＝4．‎ ‎∴L：y＝﹣x2+4x，‎ ‎∴L的对称轴x＝2，‎ 当x＝2吋，y＝x﹣4＝﹣2，‎ ‎∴L的对称轴与a的交点为（2，﹣2 ）；‎ ‎ （2）y＝﹣（x﹣）2+，‎ ‎∴L的顶点C（）‎ ‎∵点C在l下方，‎ ‎∴C与l的距离b﹣＝﹣（b﹣2）2+1≤1，‎ ‎∴点C与1距离的最大值为1；‎ ‎（3）由題意得，即y1+y2＝2y3，‎ ‎ 得b+x0﹣b＝2（﹣x02+bx0）‎ 解得x0＝0或x0＝b﹣．但x0#0，取x0＝b﹣，‎ 对于L，当y＝0吋，0＝﹣x2+bx，即0＝﹣x（x﹣b），‎ 解得x1＝0，x2＝b，‎ ‎∵b＞0，‎ ‎∴右交点D（b，0）．‎ ‎∴点（x0，0）与点D间的距离b﹣（b﹣）＝‎ ‎（4）①当b＝2019时，抛物线解析式L：y＝﹣x2+2019x ‎ 直线解析式a：y＝x﹣2019‎ 联立上述两个解析式可得：x1＝﹣1，x2＝2019，‎ ‎∴可知每一个整数x的值 都对应的一个整数y值，且﹣1和2019之间（包括﹣1和﹣2019）共有2021个整数；‎ ‎∵另外要知道所围成的封闭图形边界分两部分：线段和抛物线，‎ ‎∴线段和抛物线上各有2021个整数点 ‎∴总计4042个点，‎ ‎∵这两段图象交点有2个点重复重复，‎ ‎∴美点”的个数：4042﹣2＝4040（个）；‎ ‎②当b＝2019.5时，‎ 抛物线解析式L：y＝﹣x2+2019.5x，‎ 直线解析式a：y＝x﹣2019.5，‎ 联立上述两个解析式可得：x1＝﹣1，x2＝2019.5，‎ ‎∴当x取整数时，在一次函数y＝x﹣2019.5上，y取不到整数值，因此在该图象上“美点”为0；‎ 在二次函数y＝﹣x2+2019.5x图象上，当x为偶数时，函数值y可取整数，可知﹣1到2019.5之 间有1010个偶数，因此“美点”共有1010个．‎ 故b＝2019时“美点”的个数为4040个，b＝2019.5时“美点”的个数为1010个．‎