- 2021-05-13 发布 |
- 37.5 KB |
- 15页


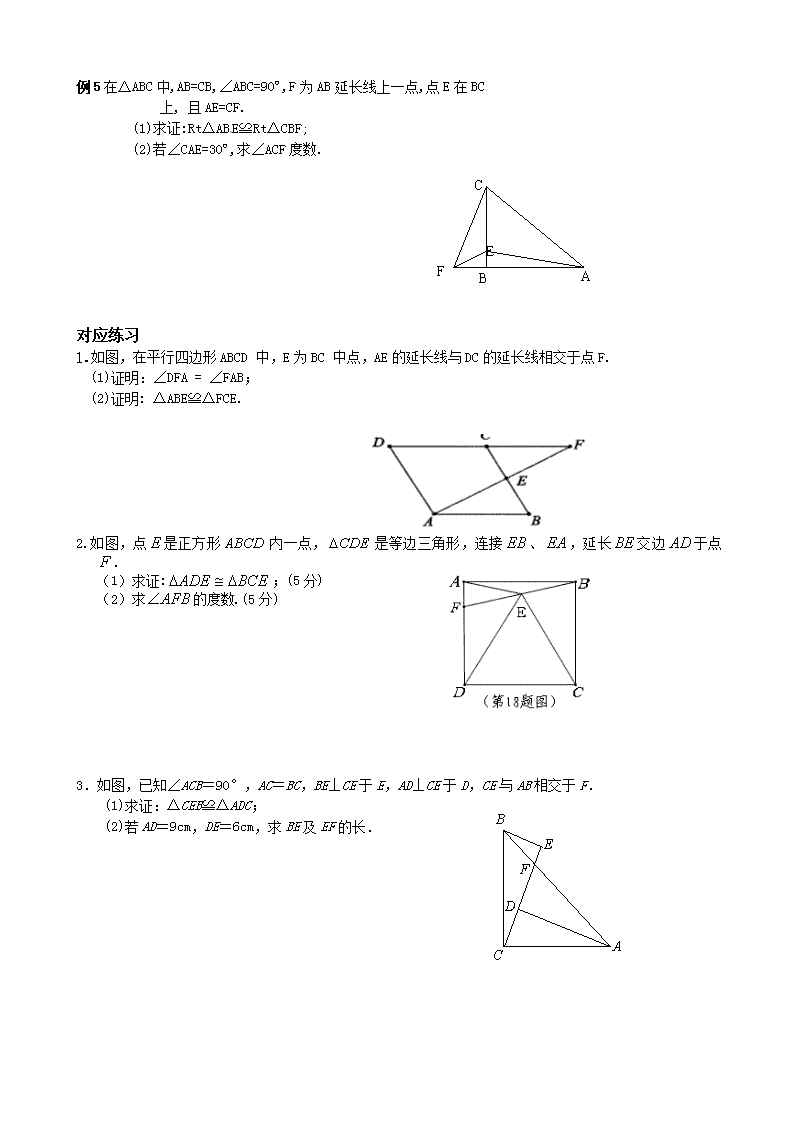
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学几何专题复习
专题 几何专题 题型一考察概念基础知识点型 例1如图1,等腰△ABC的周长为21,底边BC = 5,AB的垂直平分线是DE,则△BEC的周长为 。 例2 如图2,菱形中,,、是、的中点,若,菱形边长是______. 图1 图2 图3 例3 已知AB是⊙O的直径,PB是⊙O的切线,AB=3cm,PB=4cm,则BC= . 题型二折叠题型:折叠题要从中找到对就相等的关系,然后利用勾股定理即可求解。 例4 分别为,边的中点,沿 折叠,若,则等于 。 例5如图4.矩形纸片ABCD的边长AB=4,AD=2.将矩形纸片沿 EF折叠, 使点A与点C重合,折叠后在其一面着色(图),则着色部分的面积为( ) A. 8 B. C. 4 D. A B C D E G F F 图4 图5 图6 【题型三】涉及计算题型:常见的有应用勾股定理求线段长度,求弧长,扇形面积及圆锥体积,侧面积,三角函数计算等。 例6如图3,P为⊙O外一点,PA切⊙O于A,AB是⊙O的直径,PB交⊙O于C, PA=2cm,PC=1cm,则图中阴影部分的面积S是 ( ) A. B C D 图3 【题型四】证明题型: 第二轮复习之几何(一)——三角形全等 【判定方法1:SAS】 例1如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且 AE=AF。 求证:△ACE≌△ACF A D F E B C 例2 在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED. (1)求证:△BEC≌△DEC; (2)延长BE交AD于F,当∠BED=120°时,求∠EFD的度数. A F D E B C 【判定方法2:AAS(ASA)】 D C B A E F G 例3 如图,ABCD是正方形,点G是BC上的任意一点,于 E,,交 AG于F,求证:. 例4如图,在□ABCD中,分别延长BA,DC到点E,使得AE=AB, CH=CD连接EH,分别交AD,BC于点F,G。求证:△AEF≌△CHG. 【判定方法3:HL(专用于直角三角形)】 例5在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC 上, 且AE=CF. (1)求证:Rt△ABE≌Rt△CBF; (2)若∠CAE=30º,求∠ACF度数. A B C E F 对应练习 1.如图,在平行四边形ABCD 中,E为BC 中点,AE的延长线与DC的延长线相交于点F. (1)证明:∠DFA = ∠FAB; (2)证明: △ABE≌△FCE. 2.如图,点是正方形内一点,是等边三角形,连接、,延长交边于点. (1)求证:;(5分) (2)求的度数.(5分) A B C D F E 3.如图,已知∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,CE与AB相交于F. (1)求证:△CEB≌△ADC; (2)若AD=9cm,DE=6cm,求BE及EF的长. 第二轮复习之几何(二)——三角形相似 Ⅰ.三角形相似的判定 例1如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E, 连接DE,F为线段DE上一点,且∠AFE=∠B. (1)求证:△ADF∽△DEC (2)若AB=4,AD=3,AE=3,求AF的长. 例2如图9,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF。 (1)求证:∠ADP=∠EPB; (2)求∠CBE的度数; (3)当的值等于多少时.△PFD∽△BFP?并说明理由. 2.相似与圆结合,注意求证线段乘积,一般是转化证它所在的三角形相似。 将乘积式转化为比例式→比例式边长定位到哪个三角形→找条件证明所在的三角形相似 例3 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D. 求证:(1)D是BC的中点; (2)△BEC∽△ADC; (3)BC2=2AB•CE. 3.相似与三角函数结合, ①若题目给出三角函数值一般会将给出的三角函数值用等角进行转化,然后求线段的长度 ②求某个角的三角函数值,一般会先将这个角用等角转化,间接求三角函数值 例4如图,点E是矩形ABCD中CD边上一点,⊿BCE沿BE折叠为⊿BFE,点F落在AD上.(1)求证:⊿ABE∽⊿DFE;(2)若sin∠DFE=,求tan∠EBC的值. 练习 一、选择题 1、如图1,将非等腰的纸片沿折叠后,使点落在边上的点处.若点 为边的中点,则下列结论:①是等腰三角形;②;③是的中位线,成立的有( ) A.①② B.①③ C.②③ D.①②③ 图1 图2 2.如图,等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( ) A.45° B.55° C.60° D.75° 3.如图3,在中,,,点为的中点,,垂足为点,则等于( ) A. B. C. D. D 图3 图4 图5 4.如图4,⊿ABC和⊿CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②S⊿ABC+S⊿CDE≧S⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是( ) (A)1个 (B)2个 (C)3个 (D)4个 5.如图5,等边三角形ABC中,D、E分别为AB、BC边上的两个动点,且总使AD=BE,AE与CD交于点F,AG⊥CD于点G,则 . 6.如图6,已知点A、B、C、D均在已知圆上,AD∥BC,AC 平分∠BCD, ∠ADC = 120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) A. B. C. D. A O B C X Y 图6 图7 7.如图7,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点 处。已知,,则点的坐标是( )。 A、(,) B、(,) C、(,) D、(,) 三、解答题 1如图,矩形ABCD中,点E是BC上一点,AE=A C B D P Q AD,DF⊥AE于F,连结DE. 求证:DF=DC. 2.如图,四边形ABCD是矩形,△PBC和△QCD都是等边三角形,且点P在矩形上方,点Q在矩形内.求证:(1)∠PBA=∠PCQ=30°;(2)PA=PQ. 3.如图9,已知点D为等腰直角△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA. (1)求证:DE平分∠BDC;(2)若点M在DE上,且DC=DM,求证: ME=BD. 4.如图5AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.求证:(1)∠AOC=2∠ACD; (2)AC2=AB·AD. 、 5.把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG。 (1)求证:△BHE≌△DGF; (2)若AB=6cm,BC=8cm,求线段FG的长。 6.如图8,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将 一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合, 连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想. A B C D E 第二轮复习之几何(三)——四边形 A B C D E F 例1 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等 边△ABE。已知∠BAC=30º,EF⊥AB,垂足为F,连结DF。 (1)试说明AC=EF; (2)求证:四边形ADFE是平行四边形。 例2如图,AD∥FE,点B、C在AD上,∠1=∠2,BF=BC ⑴求证:四边形BCEF是菱形 ⑵若AB=BC=CD,求证:△ACF≌△BDE 例3如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一 点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2 , ∠3=∠4. (1)证明:△ABE≌△DAF; (2)若∠AGB=30°,求EF的长. 例4如图,在等腰梯形中,已知,,, 延长到,使. (1)证明:; D A B E C F (2)如果,求等腰梯形的高的值. 【对应练习】 1.如图,在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ. (1)求证:△BDQ≌△ADP; (2)已知AD=3,AP=2,求cos∠BPQ的值(结果保留根号). 2、如图,是四边形的对角线上两点,. 求证:(1). (2)四边形是平行四边形. A B D E F C 3. 如罔7,在一方形ABCD中.E为对角线AC上一点,连接EB、ED, (1)求证:△BEC≌△DEC: (2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数. 4.如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M. (1)求证:△AMD≌△BME; (2)若N是CD的中点,且MN=5,BE=2,求BC的长. 第二轮复习之几何(四)——圆 Ⅰ、证线段相等 A C B D E F O 例1:如图,AB是⊙O的直径,C是的中点,CE⊥AB于 E,BD交CE于点F. (1)求证:CF =BF;(2)若CD =6, AC =8,则⊙O的半径为 ___ ,CE的长是 ___ . 2、证角度相等 例2如图,是⊙O的直径,为圆周上一点,,过点的切线与的延长线交于点.:求证:(1);(2)≌. 3、证切线 点拨:证明切线的方法——连半径,证垂直。根据:过半径的外端且垂直于半径的直线是圆的切线 例7图 例3如图,四边形ABCD内接于⊙O,BD是⊙O的直径, AE⊥CD于点E,DA平分∠BDE。 (1)求证:AE是⊙O的切线。 (2)若∠DBC=30°,DE=1cm,求BD的长。 例4如图,点A、B、C、D都在⊙O上,OC⊥AB,∠ADC=30°. (1)求∠BOC的度数; (2)求证:四边形AOBC是菱形. 对应练习 1.FM A DO EC O C B 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的 延长线相交于点F,且AD=3,cos∠BCD= . (1)求证:CD∥BF; (2)求⊙O的半径; (3)求弦CD的长. 2.如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上, 且AB=AD=AO. (1)求证:BD是⊙O的切线. (2)若点E是劣弧BC上一点,AE与BC相交于点F, 且△BEF的面积为8,cos∠BFA=,求△ACF的面积. 1.一副三角板,如图所示叠放在一起,则图中∠的度数是( ) A. B. C. D. 图1 图2 2.如图2,在边长为4的等边三角形ABC中,AD是BC边上的高,点E、F是AD上的两点,则图中阴影部分的面积是( ) A.4 B.3 C.2 D. 3.如图3,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是 6 8 C E A B D 图3 图4 (A)3.5 (B)4.2 (C)5.8 (D)7 4. 如图4,直角三角形纸片的两直角边长分别为6,8,现将如图那样折叠,使点与点重合,折痕为,则的值是( ) A. B. C. D. 5.如图5,是等腰直角三角形,是斜边,将绕点逆时针旋转后,能与 重合,如果,那么的长等于( ) A. B. C. D. 6. 图6,已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80º ,则∠EGC的度数为 图5 图6 7.如图,已知:在平行四边形ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=______cm. 8.如图,矩形ABCD中,AB=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连接CE,则CE的长________. 9.如图,BD是⊙O的直径,OA⊥OB,M是劣弧上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于点N。 (1)求证:PM=PN; (2)若BD=4,PA=AO,过B点作BC∥MP交⊙O于C点,求BC的长. 10.如图,在△ABC中,以AB为直径的⊙O交BC于点P,PD⊥AC于点D,且PD与⊙O相切. (1)求证:AB=AC;(2)若BC=6,AB=4,求CD的值. C B A O P D 11.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠ E=45°,∠A=60°,AC=10,试求CD的长. 12.如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90o,且EF交正方形外角的平分线CF于点F. (1)证明:∠BAE=∠FEC; (2)证明:△AGE≌△ECF; (3)求△AEF的面积. 13.如图,矩形中,.点是上的动点,以为直径的与交于点,过点作于点. (1)当是的中点时: ①的值为______________; ② 证明:是的切线; (2)试探究:能否与相切?若能,求出此时的长;若不能,请说明理由. D E O C B G F A 几何之——解直角三角形 1在△ABC中,∠C=90°,sinA=,则tanB=( ) A. B. C. D. 2、在∆ABC中,若|sinA- |+(-cosB)2=0, ∠A.∠B都是锐角,则∠C的度数是( ) A. 750 B. 900 C.1050 D.1200 3、如下左图,在△ABC中,∠C=90°,AB=13,BC=5,则sinA的值是( ) A、 B、 C、 D、 4如上右图,在四边形ABCD中,E、F分別是AB、AD的中点,若EF=2, BC=5,CD=3,则tanC等于( ) A、 B、 C、 D、 5、如,在矩形ABCD中,DE⊥AC于E,设∠ADE=,且, AB = 4, 则AD的长为( ). (A)3 (B) (C) (D) 6在锐角△ABC中,∠BAC=60°,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DF=EF;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=DE中,一定正确的有( ) A、2个 B、3个 C、4个 D、5个 7.= 8.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为米,则这 个破面的坡度为 . A B C D αA 9.如图,已知直线∥∥∥,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则 . 直角三角形常见模型 1 张华同学在学校某建筑物的C点处测得旗杆顶部A点的仰角为30°,旗杆底部B点的俯角为45°.若旗杆底部B点到建筑物的水平距离BE=9米,旗杆台阶高1米,试求旗杆AB的高度。 2.海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45方向,求此时灯塔B到C处的距离。 3某年入夏以来,松花江哈尔滨段水位不断下降,一条船在松花江某段自西向东沿直线航行,在A处测得航标C在北偏东60°方向上。前进100m到达B处,又测得航标C在北偏东45°方向上(如图),在以航标C为圆心,120m为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险? A D B E 图6 i=1: C 4如图6,梯形ABCD是拦水坝的横断面图,(图中是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:≈1.732,≈1.414)查看更多