中考数学专题几何应用型问题
几何应用型问题
一、选择题
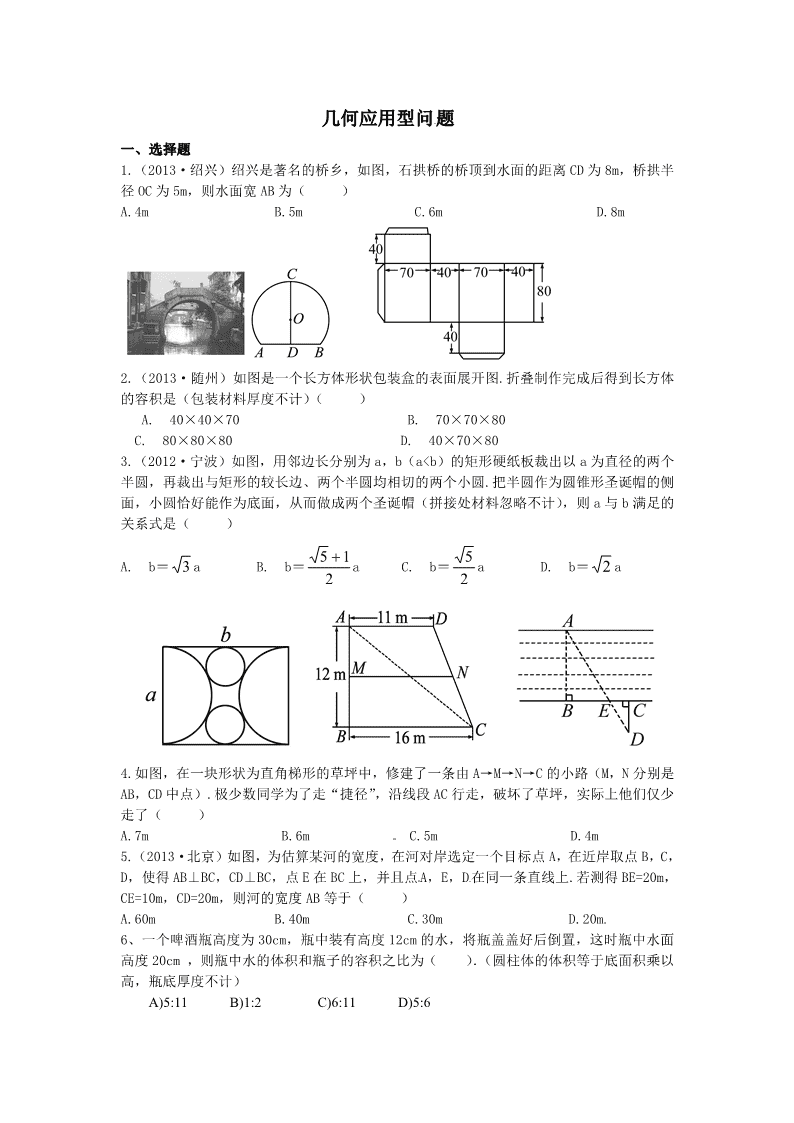
1.(2013·绍兴)绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离 CD 为 8m,桥拱半
径 OC 为 5m,则水面宽 AB 为( )
A.4m B.5m C.6m D.8m
2.(2013·随州)如图是一个长方体形状包装盒的表面展开图.折叠制作完成后得到长方体
的容积是(包装材料厚度不计)( )
A. 40×40×70 B. 70×70×80
C. 80×80×80 D. 40×70×80
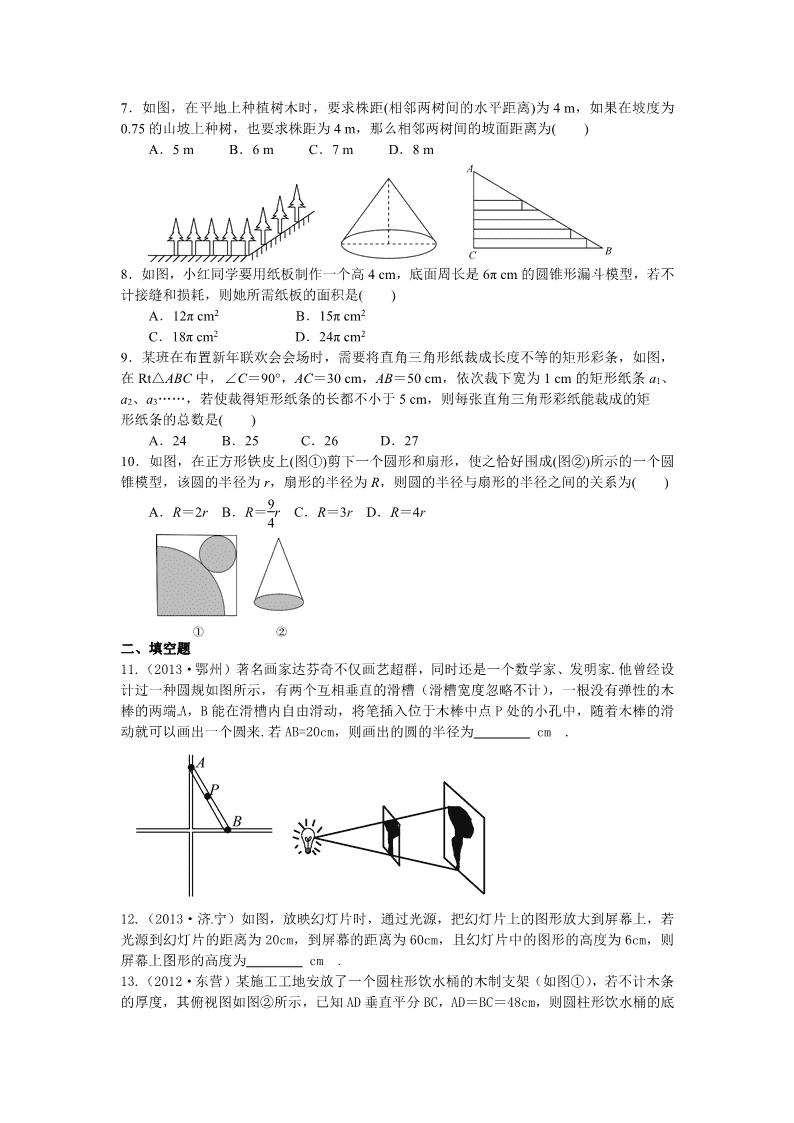
3.(2012·宁波)如图,用邻边长分别为 a,b(a
AB),影长的最大值为 m,最小值为 n,那么下列结论:①m>AC;②m=AC;③n
=AB;④影子的长度先增大后减小.其中,正确的结论的序号是__________.
三、解答题
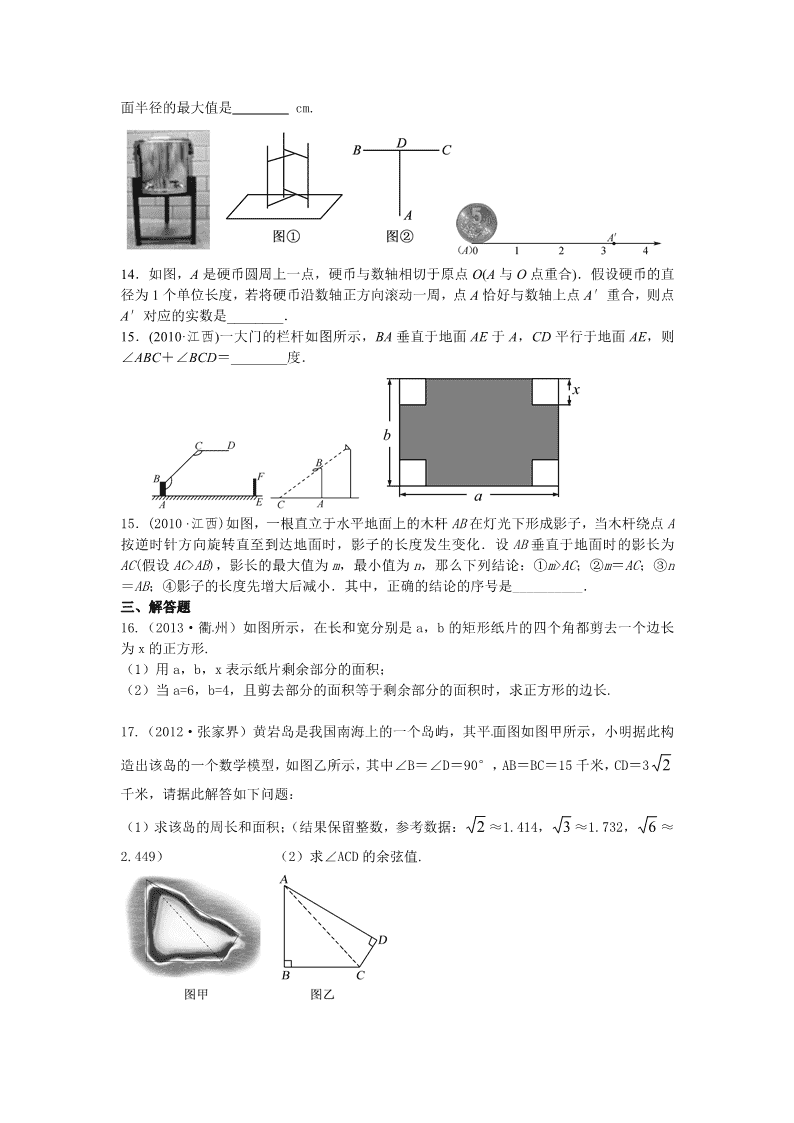
16.(2013·衢 州)如图所示,在长和宽分别是 a,b 的矩形纸片的四个角都剪去一个边长
为 x 的正方形.
(1)用 a,b,x 表示纸片剩余部分的面积;
(2)当 a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
17.(2012·张家界)黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构
造出该岛的一个数学模型,如图乙所示,其中∠B=∠D=90°,AB=BC=15 千米,CD=3 2
千米,请据此解答如下问题:
(1)求该岛的周长和面积;(结果保留整数,参考数据: 2 ≈1.414, 3 ≈1.732, 6 ≈
2.449) (2)求∠ACD 的余弦值.
18.(2013·济宁)钓鱼岛及其附属岛屿是中国固有领土(如图①),A,B,C 分别是钓鱼岛、
南小岛、黄尾屿上的点(如图②),点 C 在点 A 的北偏东 47°方向,点 B 在点 A 的南偏东 79°
方向,且 A,B 两点的距离约为 5.5km;同时,点 B 在点 C 的南偏西 36°方向.若一艘中国渔
船以 30km/h 的速度从点 A 驶向点 C 捕鱼,需要多长时间到达(结果保留小数点后两位)?
(参考数据:sin54°≈0.81,cos54°≈0.59,tan47°≈1.07,tan36°≈0.73,tan11°
≈0.19)
19.如图,路灯(P 点)距地面 8 米,身高 1.6 米的小明从距路灯的底部(O 点)20 米的 A 点,
沿 OA 所在的直线行走 14 米到 B 点时,身影的长度是变长了还是变短了?变长或变短了多
少米?
20.(2011·成都)某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙
(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形 ABCD.已知木栏总长
为 120m,设 AB 边的长为 x m,长方形 ABCD 的面积为 S(m2).
(1)求 S 与 x 之间的函数关系式(不要求写出自变量 x 的取值范围).当 x 为何值时,S 取
得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别
为 O1 和 O2,且 O1 到 AB、BC、AD 的距离与 O2 到 CD、BC、AD 的距离都相等,并要求在
苗圃内药材种植区域外四周至少要留够 0.5m 宽的平直路面,以方便同学们参观学习.当(1)
中 S 取得最大值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理
由.
解 (1)S=x(120-2x)=-2(x-30)2+1800,当 x=30 时,S 取最大值为 1800.
(2)如图所示,过 O1、O2 分别作到 AB、BC、AD 和 CD、BC、AD 的垂线,垂足如图,
根据题意可知,O1E=O1F=O1J=O2G=O2H=O2I;当 S 取最大值时,AB=CD=30,BC=
60,
∴O1F=O1J=O2G=O2I=1
2AB=15,
∴O1E=O2H=15,
∴O1O2=EH-O1E-O2H=60-15-15=30,
∴两个等圆的半径为 15,由于圆 O1、圆 O2 相切,所以左右不能够留 0.5 米的平直路面.
∴设计不可行.
21.(2011·江西)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形,当点 O
到 BC(或 DE)的距离大于或等于⊙O 的半径时(⊙O 是桶口所在圆,半径为 OA),提手才能从
图甲的位置转到图乙的位置,这样的提手才合格.现用金属材料做了一个水桶提手(如图丙
A-B-C-D-E-F,C-D 是圆弧,其余是线段),O 是 AF 的中点,桶口直径 AF=34 cm,
AB=FE=5 cm,∠ABC =∠FED =149°.请通过计算判断这个水桶提手是否合格.
(参考数据: 314≈17.72,tan 73.6°≈3.40,sin 75.4°≈0.97.)
解 解法一:
如图,连接 OB,过点 O 作 OG⊥BC 于点 G.
在 Rt△ABO 中,AB=5,AO=AF
2
=17,
∴ tan∠ABO=AO
AB
=17
5
=3.4,
∴∠ABO=73.6°,
∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°.
又 ∵OB= 52+172= 314≈17.72,
∴在 Rt△OBG 中,
.OG=OB·sin∠OBG=17.72×0.97≈17.19>17.
∴水桶提手合格.
解法二:
如图,连接 OB,过点 O 作 OG⊥BC 于点 G.
在 Rt△ABO 中,AB=5,AO=17,
∴ tan∠ABO=AO
AB
=17
5
=3.4,
∴∠ABO=73.6°.
要使 OG≥OA,只需∠OBC≥∠ABO,
∵∠OBC=∠ABC-∠ABO=149°-73.6°=75.4°>73.6°,
∴水桶提手合格.
22(2008 眉山)要挖掘地下文物,需测出文物离地面的距离.如图,考古队在文物上方地面 A
处用仪器测文物 C,探测线与地面夹角为 30°,在沿文物方向前进 20 米的 B 处,又测得探测线
与地面夹角为 60°,求文物 C 到地面的距离.
23(2008 莱芜)如图,AC 是某市环城路的一段,AE,BF,CD 都是南北方向的街道,其与环
城路 AC 的交叉路口分别是 A,B,C.经测量花卉世界 D 位于点 A 的北偏东 45°方向,点 B 的
北偏东 30°方向上,AB=2km,∠DAC=15°.
(1)求 B,D 之间的距离;
(2)求 C,D 之间的距离.
24 如图,甲船在港口 P 的北偏西 60 方向,距港口80 海里的 A 处,沿 AP 方向以 12 海里/
时的速度驶向港口 P .乙船从港口 P 出发,沿北偏东 45 方向匀速驶离港口 P ,现两船同
时出发,2 小时后乙船在甲船的正东方向.求乙船的航行速度.(精确到 0.1 海里/时,参考
数据 2 1.41≈ , 3 1.73≈ )
A
P 东
北
4560
25、探究规律:如图 1,已知直线 m ∥ n ,A、B 为直线 n 上的两点,C、P 为直线 m 上的
两点。
( 1 ) 请 写 出 图 中 面 积 相 等 的 各 对 三 角
形: 。
(2)如果 A、B、C 为三个定点,点 P 在 m 上移动,那么无论 P 点移动到任何位置总
有:
与△ABC 的面积相等;
理由是:
。
n
m
第 26 题图 1
O
BA
PC
n
m
第 26 题图2
E
D
C
B
A n
m
第 26 题图 3
N
M
E
D
CB
A
解决问题:
如图 2,五边形 ABCDE 是张大爷十年前承包的一块土地的示意图,经过多年开垦荒地,
现已变成如图 3 所示的形状,但承包土地与开垦荒地的分界小路(图 3 中折线 CDE)还保
留着,张大爷想过 E 点修一条直路,直路修好后,要保持直路左边的土地面积与承包时的
一样多。请你用有关的几何知识,按张大爷的要求设计出修路方案。(不计分界小路与直路
的占地面积)
(1)写出设计方案,并在图 3 中画出相应的图形;
(2)说明方案设计理由。
26.探究规律:(1)△ABC 和△ABP, △AOC 和△BOP, △CPA 和△CPB;
(2) △ABP.
因为平行线间的距离相等,所以无论点 P 在 m 上移动到任何△ABP 与△ABC 同底等高,因
此,它们的面积总相等.
解决问题:(1)画法如图.
连结 EC, 过点 D 作 DF//EC, 交 CM 于点 F, 连结 EF, EF 即为所求直路的位置.
(2)设 EF 交 CD 于点 H,
由上面得到的结论,可知:
S△ECF=S△ECD, S△HCF=S△EDH.
∴S 五边形 ABCDE=S 五边形 ABCFE,
S 五边形 EDCMN= S 四边形 EFMN.
A
B
C
D
E
F
M
N