2018东营市中考数学试题全真模拟

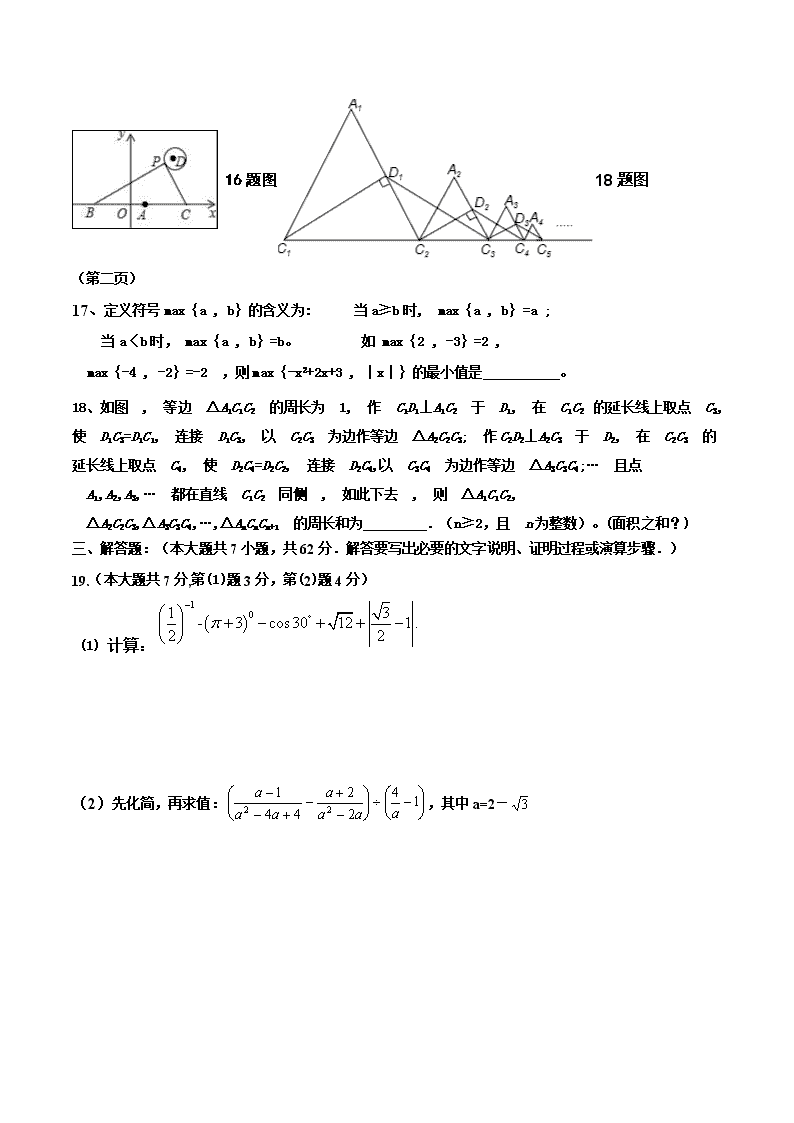
2018东营市中考数学试题全真模拟

‎2018东营市中考数学试题 全真模拟 ‎ ‎ （总分120分 考试时间120分钟）‎ 二、填空题：（本大题、共8小题，其中11－14题每小题3分，15－18题每小题4分，共28分．只 要求填写最后结果．）‎ ‎11. 据媒体报道，我国最新研制的“察打一体”无人机的速度极快，经测试最高速度可达‎204000米/分，204000这个数用科学记数法表示为________．‎ ‎12、因式分解：x2－2x＋(x－2)＝________．‎ ‎13. 若关于x、y的二元一次方程组的解满足x＋y>0，则m的取值范围是________． ‎ 一、选择题：（本大题共10小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分，共计30分。）‎ ‎1．计算：|－|的倒数是(　　) A. B. － C. 3 D. －3‎ ‎2、下列计算正确的是(　　)A. －＝ B. (a＋b)2＝a2＋b‎2 C. x6÷x2＝x3 D. 2x2·3x4＝6x6‎ ‎3．如图，直线a∥b，直线c与直线a，b分别交于点D，E，射线DF⊥直线c，则图中与∠1互余的角有(　　) A. 4个 B. 3个 C. 2个 D. 1个 ‎3题图 4题图 6题图 ‎ ‎4．已知：如图，是由若干个大小相同的小正方体所搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是(　　) A. 6个 B. 7个 C. 8个 D. 9个 ‎5．已知关于x的分式方程+=1的解是非负数，则m的取值范围是（　　） ‎ A．m＞2 B．m≥‎2 ‎C．m＞2且m≠3 D． m≥2且m≠3‎ ‎6、如图,从一块圆形纸片上剪出一个圆心角为的扇形ABC,使点A、B、C在圆周上, 将剪下的扇形作为一个圆锥侧面,如果圆锥的高为,则这块圆形纸片的直径为(   )‎ A、‎12cm B、‎20cm C、‎24cm D、‎‎28cm ‎7、下列说法中 ‎①一个角的两边分别垂直于另一角的两边，则这两个角相等或互补 ‎②若点A在y=2x﹣3上，且点A到两坐标轴的距离相等，则点A在第一象限 ‎③半径为5的圆中，弦AB=8，则圆周上到直线AB的距离为2的共有四个 ‎④如果AD是△ABC的高，∠CAD=∠B，那么△ABC是直角三角形 正确命题有（　　） A．0个   B．1个  C．2个  D．3个 ‎8、今年学校举行足球联赛，共赛17轮（即每队均需参赛17场），记分办法是：胜1场得3分，平1场得1分，负1场得0分．在这次足球比赛中，小虎足球队得16分，且踢平场数是所负场数的整数倍，则小虎足球队所负场数的情况有（　 ）种 A、6 B、‎5 C、4 D、3 （第一页）‎ ‎9、如图，已知△ABC中，∠C=90°，AC=BC=√2，将△ABC绕点A顺时针方向旋转60°到的位置，连接，则的长为（   ）。A、 B、 C、 D、1‎ ‎ 9题图 10题图 ‎10、如图,在菱形ABCD中, AB=6, ∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2 ,连接CF.以下结论:①∠BAF=∠BCF ; ②点E到AB的距离是 2√3; ③S△CDF：S△BEF=9：4 ; ‎ ‎ ④tan∠DCF=3/7 . 其中正确的有(  )A、4个 B、3个 C、2个 D、1个 二、填空题：（本大题、共8小题，其中11－14题每小题3分，15－18题每小题4分，共28分．只 要求填写最后结果．）‎ ‎11. 据媒体报道，我国最新研制的“察打一体”无人机的速度极快，经测试最高速度可达‎204000米/分，204000这个数用科学记数法表示为________．‎ ‎12、因式分解：x2－2x＋(x－2)＝________．‎ ‎13. 若关于x、y的二元一次方程组的解满足x＋y>0，则m的取值范围是________． ‎ ‎14、有9张卡片，分别写有这九个数字，将它们背面朝上洗匀后，任意抽出一张，记卡片上的数字为a，则关于x的不等式组有解的概率为________.‎ ‎15、在平行四边形ABCD中，BC边上的高为4，AB=5，AC=2，则▱ABCD的周长等于　 　．‎ ‎16. 如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是　 　．‎ ‎ 16题图18题图 ‎（第二页）‎ ‎17、定义符号max﹛a , b﹜的含义为: 当a≥b时, max﹛a , b﹜=a ; ‎ 当a〈b时， max﹛a , b﹜=b。 如 max﹛2 , -3﹜=2 , ‎ ‎ max﹛-4 , -2﹜=-2 ，则max﹛-x2+2x+3 , ｜x｜﹜的最小值是　 　。‎ ‎18、如图 , 等边 △A‎1C1C2 的周长为 1, 作 C1D1⊥A‎1C2 于 D1, 在 C‎1C2 的延长线上取点 C3, 使 D‎1C3=D‎1C1, 连接 D‎1C3, 以 C‎2C3 为边作等边 △A‎2C2C3; 作C2D2⊥A‎2C3 于 D2, 在 C‎2C3 的延长线上取点 C4, 使 D‎2C4=D‎2C2, 连接 D‎2C4,以 C‎3C4 为边作等边 △A‎3C3C4;… 且点 A1,A2,A3,… 都在直线 C‎1C2 同侧 , 如此下去 , 则 △A‎1C1C2,‎ ‎△A2C2C3,△A3C3C4,…,△AnCnCn+1 的周长和为　 　．（n≥2，且 n为整数）。(面积之和？)‎ 三、解答题：（本大题共7小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤．）‎ ‎19.（本大题共7分,第(1)题3分，第(2)题4分）‎ ‎ (1) 计算：‎ ‎（2）先化简，再求值：，其中a=2－‎ ‎ ‎ ‎20.（本题8分）为了解某校落实新课改精神的情况,现以该校九年级二班的同学参加课外活动的情况为样本,对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计,并绘制了如图所示的统计图. ‎ ‎(1)参加音乐类活动的学生人数为  　人,参加球类活动的人数的百分比为  。(2)请把图2(条形统计图)补充完整; ‎ ‎(3)该校学生共600人,则参加棋类活动的人数约为 。 ‎ ‎ (4)该班参加舞蹈类活动的4位同学中,有1位男生(用E表示)和3位女生(分别用F,G,H表示),先准备从中选取两名同学组成舞伴,请用列表或画树状图的方法求恰好选中一男一女的概率. ‎ ‎（第三页）‎ ‎21.（本题8分）如图，已知AB是⊙O的直径，点C为圆上一点，点D在OC的延长线上，连接DA，‎ 交BC的延长线于点E，使得∠DAC=∠B．‎ ‎（1）求证：DA是⊙O切线；‎ ‎（2）求证：△CED∽△ACD；‎ ‎（3）若OA=1，sinD=，求AE的长．‎ ‎（第四页）‎ ‎22.（本题8分）东营市公交公司将淘汰所有线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元。‎ ‎（1）求购买A型和B型公交车每辆各需多少万元？‎ ‎（2）预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次。若该公司购买A型和B型公交车的总费用不超过1220万元，且确保这10辆公交车在该线路的年均载客总和不少于650万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？‎ ‎ ‎ ‎ ‎ ‎23.（本题9分）如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=k/x (k≠0)的图象相交于点B（3,2）、C（—1，n）‎ ‎(1)求一次函数和反比例函数的解析式;  ‎ ‎(2)根据图象,直接写出y1＞y2时x的取值范围; ‎ ‎(3)在y轴上是否存在点P,使△PAB为直角三角形?如果存在,请求点P的坐标;若不存在,请说明理由.‎ ‎ ‎ ‎（第五页） ‎ ‎24.（本题10分）如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.    (1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形; ‎ ‎(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.‎ ‎(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM ‎①求∠CAM的度数;  ②当FH=√3, DM=4时,求DH的长.‎ ‎ ‎ ‎（第六页）‎ ‎25、（本题12分）如图，已知：关于x的二次函数的图象与x轴交于点A(1，0)和点B，与y轴交于点C(0，3)，抛物线的对称轴与x轴交于点D.‎ ‎ (1)求二次函数的表达式； (3分)‎ ‎ (2)在y轴上是否存在一点P，使△PBC为等腰三角形.若存在，请求出点P的坐标； (4分)‎ ‎ (3)有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到 达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积. (5分)‎ x y O A B C D N M 第25题图 ‎ ‎ ‎（第七页）‎ ‎2018东营市中考数学试题 全真模拟 答案 ‎ 1、 C 2、D 3、A 4、B 5、D 6、C 7、B 8、D 9、A 10、B ‎11、2.04x105 12、(x-2)(x+1) 13、m＞-2 14、 ‎ ‎15、12或20 16、6 17、（√21-3）/2 18、(2n−1)/(2n−1)‎ ‎19、解：（1）原式=2-1- +2 +1- =2+ ；‎ 解(2)：原式，将代入，得：原式。‎ ‎20、解:(1)本次调查的总人数为(人),‎ 参加音乐类活动的学生人数为人,参加球类活动的人数的百分比为, 因此，本题正确答案是: 7、; ‎ ‎(2)补全条形图如下:‎ ‎(3)该校学生共600人,则参加棋类活动的人数约为, ‎ 因此，本题正确答案是:105;‎ ‎(4)画树状图如下: ‎ ‎ ‎ 共有12种情况,选中一男一女的有6种, 则 ‎21、(1)证明:为的直径,,,‎ ‎,.‎ 是半径,为的切线 ‎(2)解:,.‎ ‎.,‎ ‎,;‎ ‎(3)解:在中,,,,‎ ‎.,‎ 又,,,‎ ‎22、（1）设购买型公交车每辆需万元，购买型公交车每辆需万元，由题意列方程得：，得：，解得，把代入得：，故方程组的解为：，所以购买型公交车每辆需万元，购买型公交车每辆需万元。‎ ‎（2）设购买型公交车辆，则购买型公交车辆，由题意列不等式组为：，去括号得：，解得；去括号得：，解得，故不等式组的解集为：，因为取整数，所以的取值为、、；则该公司有三种购车方案：①购买型公交车辆，型公交车辆，总费用为：（万元）；②购买型公交车辆，型公交车辆，总费用为：（万元）；③购买型公交车辆，型公交车辆，总费用为：万元。根据三种购买方案可知：，所以购买型公交车辆，型公交车辆费用最少，最少费用为万元 ‎23、解:(1) 把代入得:反比例函数解析式为:‎ 把代入,得: ‎ 把、分别代入,得:,解得: 所以一次函数解析式为 ‎(2) 由图可知,当写出时x的取值范围是或者 ‎(3)y轴上存在点P,使为直角三角形  如图, ‎ ‎  过B作轴于,   ,为直角三角形 此时, 过B作交y轴于 ‎,为直角三角形 在中, ‎ 在 AB和 AB ‎ ‎ 综上所述,、‎ ‎24、(1)证明:如图1中, ‎ ‎  ‎ ‎, , , , ‎ 是的中线,且D与M重合, , ‎ ‎, ,, ∴四边形ABDE是平行四边形. ‎ ‎(2)结论:成立.理由如下: ‎ 如图2中,过点M作交CE于G. ‎ ‎, 四边形DMGE是平行四边形, ,且, ‎ 由(1)可知,, ,, ‎ 四边形ABDE是平行四边形. ‎ ‎(3)①如图3中,取线段HC的中点I,连接MI, ‎ ‎ , 是的中位线, ‎ ‎,, ,且 ‎,, ‎ ‎②设,则,, , , ‎ 四边形ABDE是平行四边形, , , , 解得或(舍弃), ‎ ‎25、解:（1）由题意可得的图象过点和点，代入解析式可得：，解得，所以二次函数的表达式为：。‎ ‎（2）存在。设点，因为点的坐标为，所以且。将代入中可得：，解得，，所以点的坐标为，所以。‎ ‎①当是为等腰的底边时，则，根据两点间距离公式可得：，所以有，解得，即当点的坐标为时，为等腰三角形。‎ ‎②当为等腰底边时，则，在中，，当点在点上方时，，当点在点下方时，，即当点的坐标为或时，为等腰三角形。‎ ‎③当为等腰底边时，，由，可得：，解得或，当时点于点重合，故舍去，即当点的坐标为时，为等腰三角形。‎ 综上所述，点的坐标为：或或或时，为等腰三角形。‎ ‎（3）由可得对称轴为：，由题意设点，则当点向上运动时有，当点向下运动时有，其中。当点向上运动时，，，所以，因为，所以当时，取得最大值为，此时点坐标为，即，点的坐标为。同理可得：当向下运动时，点 坐标为，点的坐标为时，取得最大值为。综上所述，当点坐标为，点的坐标为或时，的面积最大，最大值为。‎