2012年宁夏中考数学试题及答案

2012年宁夏中考数学试题及答案

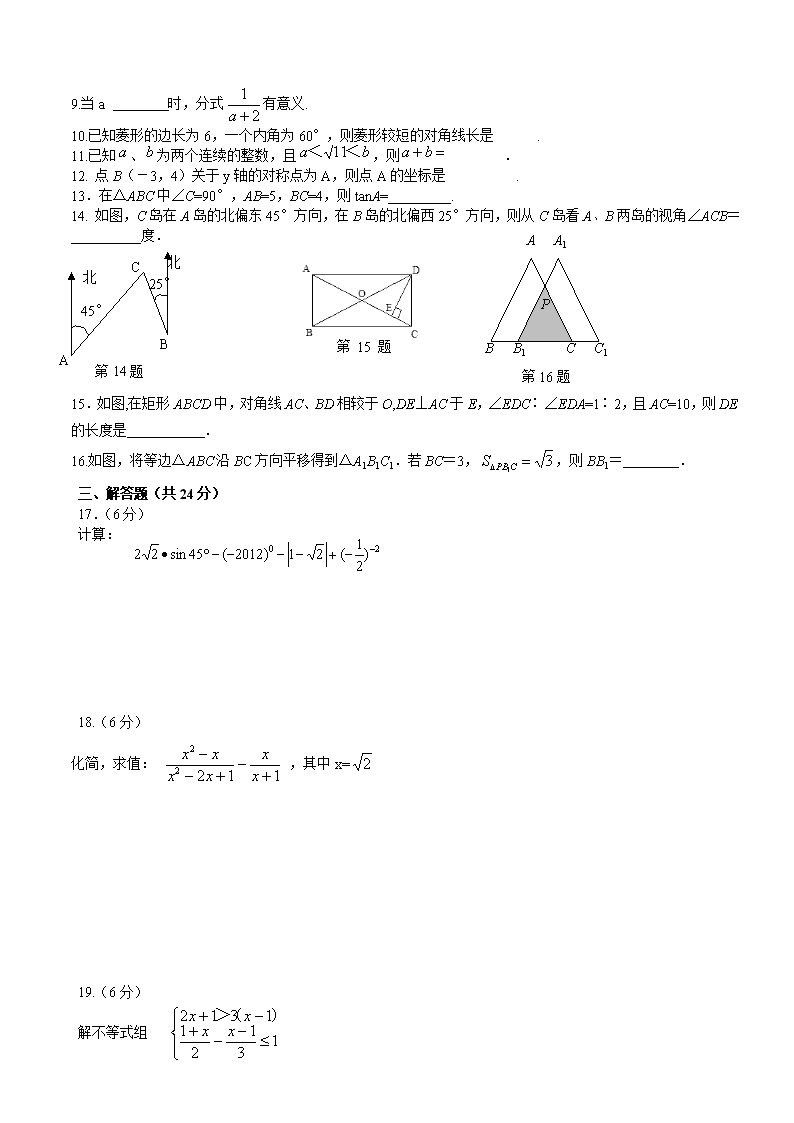
宁夏12年初中毕业暨高中阶段招生考试 数 学 试 题 一、选择题(下列每小题所给的四个答案中只有一个是正确的,每小题3分,共24分)‎ ‎1．下列运算正确的是（ ）‎ ‎ A．3－＝3 B．＝ C．＝ D．＝‎ ‎2．根据人民网-宁夏频道2012年1月18日报道，2011年宁夏地区生产总值为2060亿元，比上年增长12%，增速高于全国平均水平.2060亿元保留两个有效数字用科学记数法表示为（ ）‎ A．2.0×109元 B． 2.1×103元 C．2.1×1010元 D．2.1×1011元 ‎3．一个等腰三角形两边的长分别为4和9，那么这个三角形的周长是（ ）‎ ‎ A．13 B．17 C．22 D．17或22‎ ‎4、小颖家离学校1200米,其中有一段为上坡路，另一段为下坡路.她去学校共用了16分钟.假设小颖上坡路的平均速度是3千米/时，下坡路的平均速度是5千米/时.若设小颖上坡用了x分钟，下坡用了y分钟，根据题意可列方程组为（ ）‎ ‎ A． B． C． D．‎ ‎5.如图，一根5m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A(羊只能在草地上活动)，那么小羊A在草地上的最大活动区域面积是（ ）‎ ‎ A.πm2 B.πm2 C.πm2 D.πm2‎ 第5题 第6题 第7题 ‎6.如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则∠ACP=（　　）‎ ‎ A． B． C． D．‎ ‎7．一个几何体的三视图如图所示，网格中小正方形的边长均为1，那么下列选项中最接近这个几何体的侧面积的是（ ）‎ A．24.0 B．62.8 C．74.2 D．113.0‎ ‎8.运动会上，初二 (3)班啦啦队，买了两种价格的雪糕，其中甲种雪糕共花费40元，乙种雪糕共花费30元，甲种雪糕比乙种雪糕多20根．乙种雪糕价格是甲种雪糕价格的倍，若设甲种雪糕的价格为x元，根据题意可列方程为（ ）．‎ ‎ A． B. ‎ ‎ C． D.‎ 二、填空题（每小题3分，共24分）‎ ‎9.当a 时，分式有意义.‎ ‎10.已知菱形的边长为6，一个内角为60°，则菱形较短的对角线长是 .‎ ‎11.已知、为两个连续的整数，且，则 ．‎ ‎12. 点B（－3，4）关于y轴的对称点为A，则点A的坐标是 .‎ ‎13．在△ABC中∠C=90°，AB=5，BC=4，则tanA=_________.‎ 第16题 A A1‎ B B1‎ C C1‎ P ‎14. 如图，C岛在A岛的北偏东45°方向，在B岛的北偏西25°方向，则从C岛看A、B两岛的视角∠ACB＝__________度．‎ 北 B A C 北 ‎25°‎ ‎45°‎ 第14题 第15题图 ‎15．如图,在矩形ABCD中，对角线AC、BD相较于O,DE⊥AC于E，∠EDC∶∠EDA=1∶2，且AC=10，则DE的长度是 ．‎ ‎16.如图，将等边△ABC沿BC方向平移得到△A1B1C1．若BC＝3，，则BB1＝ ．‎ 三、解答题（共24分）‎ ‎17．（6分）‎ 计算： ‎ ‎18.（6分）‎ 化简，求值： ，其中x=‎ ‎19.（6分）‎ 解不等式组 ‎ ‎20.（6分）‎ 某商场为了吸引顾客，设计了一种促销活动，在一个不透明的箱子里放有4个相同的小球，在球上分别标有“0元”、“10元”、“20元”、“30元”的字样，规定：顾客在本商场同一天内，每消费满200元，就可以在箱子里先后摸出两个球（第一次摸出后不放回）.商场根据两小球所标金额的和，返还相应价格的购物券，可以重新在本商场消费.某顾客刚好消费200元.‎ ‎（1）该顾客至少可得到 元购物券，至多可得到 元购物券；‎ ‎（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率.‎ ‎ ‎ 四、解答题（共48分）‎ ‎ ‎ ‎21.（6分）‎ 商场对每个营业员在当月某种商品销售件数统计如下：‎ 解答下列问题 ‎（1）设营业员的月销售件数为x(单位:件),商场规定:当x＜15时为不称职；当15≤x＜20时为基本称职；当20≤x＜25为称职；当x≥25时为优秀.试求出优秀营业员人数所占百分比；‎ ‎（2）根据（1）中规定，计算所有优秀和称职的营业员中月销售件数的中位数和众数；‎ ‎（3）为了调动营业员的工作积极性，商场决定制定月销售件数奖励标准，凡达到或超过这个标准的营业员将受到奖励。如果要使得所有优秀和称职的营业员中至少有一半能获奖，你认为这个奖励标准应定为多少件合适？并简述其理由.‎ ‎ ‎ ‎ 22.（6分）‎ 在⊙O中，直径AB⊥CD于点E，连接CO并延长交AD于点F,且CF⊥AD.‎ 求∠D的度数.‎ ‎23.（8分）‎ 正方形ABCD的边长为3，E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.‎ ‎（1）求证：EF=FM ‎ ‎（2）当AE=1时，求EF的长．‎ ‎24.（8分）‎ 直线与反比例函数 (x>0)的图像交于点A，与坐标轴分别交于M、N两点，当AM=MN时,求k的值.‎ ‎ 25．（10分）‎ 某超市销售一种新鲜“酸奶”， 此“酸奶”以每瓶3元购进，5元售出.这种“酸奶”的保质期不超过一天，对当天未售出的“酸奶”必须全部做销毁处理.‎ ‎（1）该超市某一天购进20瓶酸奶进行销售.若设售出酸奶的瓶数为x（瓶），销售酸奶的利润为y（元），写出这一天销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式.为确保超市在销售这20瓶酸奶时不亏本，当天至少应售出多少瓶？‎ ‎（2）小明在社会调查活动中，了解到近10天当中，该超市每天购进酸奶20瓶的销售情况统计如下：‎ 每天售出瓶数 ‎17‎ ‎18‎ ‎19‎ ‎20‎ 频数 ‎1‎ ‎2‎ ‎2‎ ‎5‎ 根据上表，求该超市这10天每天销售酸奶的利润的平均数；‎ ‎（3）小明根据（2）中，10天酸奶的销售情况统计，计算得出在近10天当中，其实每天购进19瓶总获利要比每天购进20瓶总获利还多.你认为小明的说法有道理吗？试通过计算说明.‎ ‎26．（10分） ‎ 在矩形ABCD中，AB=2，AD=3,P是BC上的任意一点（P与B、C不重合），过点P作AP⊥PE，垂足为P，PE交CD于点E.‎ ‎(1)连接AE，当△APE与△ADE全等时，求BP的长；‎ A D B C P ‎(2)若设BP为x,CE为y，试确定y与x的函数关系式.当x取何值时，y的值最大？最大值是多少？‎ ‎(3)若PE∥BD，试求出此时BP的长.‎ E 宁参考答案及评分标准 ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C D C B D D B B 二、填空题（3分×8=24分）‎ ‎9. a≠-2；10. 6； 11. 7； 12.（3, 4）； 13.； 14. 70； 15.； 16. 1.‎ 三．解答题（共24分）‎ ‎17.解：原式=……………………………………4分 ‎ =6-………………………………………………………………6分 ‎18.解：原式= ‎ ‎ =‎ ‎ =……………………………………………………4分 当x=时 原式==………………………………………………6分 ‎19.解： 由①得 2x+1＞3x-3 ‎ 化简得 -x ＞-4‎ ‎ ∴ x＜4 ………………………………………………………………2分 由②得 3(1+ x）- 2(x-1）≤6‎ 化简得∴ x ≤ 1 ……………………………………………………5分 ‎ ∴原不等式组的解集是x≤1 …………………………………………6分 ‎20. (1)10；50 …………………………………………………………………………2分 ‎(2) 列表法：‎ ‎0‎ ‎10‎ ‎20‎ ‎30‎ ‎0‎ ‎/‎ ‎（0，10）‎ ‎（0，20）‎ ‎（0，30）‎ ‎10‎ ‎（10， 0）‎ ‎/‎ ‎（10，20）‎ ‎（10， 30）‎ ‎20‎ ‎（20， 0）‎ ‎（20，10）‎ ‎/‎ ‎（20，30）‎ ‎30‎ ‎（30，0）‎ ‎（30，10）‎ ‎（30，20）‎ ‎/‎ ‎(树状图略) ……………………………………………………………………………4分 从上表可以看出，共有12种等可能结果其中两球金额之和不低于30元的共有8种.‎ ‎∴P（获得购物卷的金额30元）= ………………………………………6分 四、解答题(共48分)‎ ‎21. 解:(1)优秀营业员人数所占百分比 …………………………2分 ‎(2)所有优秀和称职的营业员中月销售件数的中位数22、众数20. …………4分 ‎ ‎ (3) 奖励标准应定为22件.中位数是一个位置代表值，它处于这组数据的中间位置，因此大于或等于中位数的数据至少有一半.所以奖励标准应定为22件. …6分 ‎ A ‎22. 解：连接BD ‎ C B E F D O 第22题 ‎∵AB⊙O是直径 ‎ ‎∴BD ⊥AD ‎ 又∵CF⊥AD ‎∴BD∥CF ‎ ‎∴∠BDC=∠C …………………………3分 又∵∠BDC=∠BOC ‎∴∠C=∠BOC ‎∵AB⊥CD ‎∴∠C=30°‎ ‎∴∠ADC＝60°…………………………………………………………………6分 第23题 A B E F M D C ‎23. 证明：(1)∵△DAE逆时针旋转90°得到△DCM ‎∴DE=DM ∠EDM=90°‎ ‎∴∠EDF + ∠FDM=90°‎ ‎∵∠EDF=45°‎ ‎∴∠FDM =∠EDM=45°‎ ‎∵ DF= DF ‎ ‎∴△DEF≌△DMF ‎∴ EF=MF ……………………………………………………………4分 ‎ ‎（2） 设EF=x ∵AE=CM=1 ‎ ‎∴ BF=BM-MF=BM-EF=4-x ‎ ‎∵ EB=2‎ 在Rt△EBF中，由勾股定理得 即 解之，得　 …………………………………………………………8分 ‎ 24.解：过点A作AB⊥x轴， 垂足为B，对于直线y=kx+‎ 当x=0 时. ‎ ‎ 即OM= ………………………………………2分 ‎∵AM=MN ‎∴AN=2MN ‎∵Rt△MON ∽Rt△ABN ‎∴‎ ‎∴………………………………………………………………5分 将代入中得 x=1‎ ‎∴A(1, )‎ ‎∵点A在直线y=kx+上 ‎∴= k+‎ ‎∴k = …………………………………………………………………8分 ‎ 25.解（1）由题意知，这一天销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式为:y=5x-60 ………………………………………………………3分 当5x-60≥0时.x≥12‎ ‎∴当天至少应售出12瓶酸奶超市才不亏本。…………………………4分 ‎（2）在这10天当中，利润为25元的有1天，30元的有2天，35元的有2天，40元的有5天 ‎∴这10天中，每天销售酸奶的利润的平均数为 ‎（25+30×2+35×2+40×5）÷10=35.5 ………………………………7分 ‎（3）小明说的有道理. ‎ ‎∵在这10天当中,每天购进20瓶获利共计355元.‎ 而每天购进19瓶销售酸奶的利润y（元）与售出的瓶数x（瓶）之间的函数关系式为：y=5x-57‎ ‎ 在10天当中，利润为28元的有1天. 33元的有2天.38元的有7天.‎ 总获利为28+33×2+38×7=360>355 ∴小明说的有道理.………………10分 A D B C P E ‎26. 解：(1)∵△APE≌△ADE ‎ ‎∴AP=AD=3‎ 在Rt△ABP中，BP=…2分 ‎(2) ∵AP⊥PE ‎∴Rt△ABP∽Rt△PCE ‎∴ 即 ‎∴ ‎ ‎∴当 ……………6分 A D B C P E ‎(3)设BP=x, ‎ ‎∵PE∥BD ‎ ‎∴△CPE∽△CBD ‎ ‎∴ ‎ ‎ 即 化简得 解得 ‎∴当BP= 时, PE∥BD. --------------------------10分