- 2021-05-13 发布 |
- 37.5 KB |
- 13页
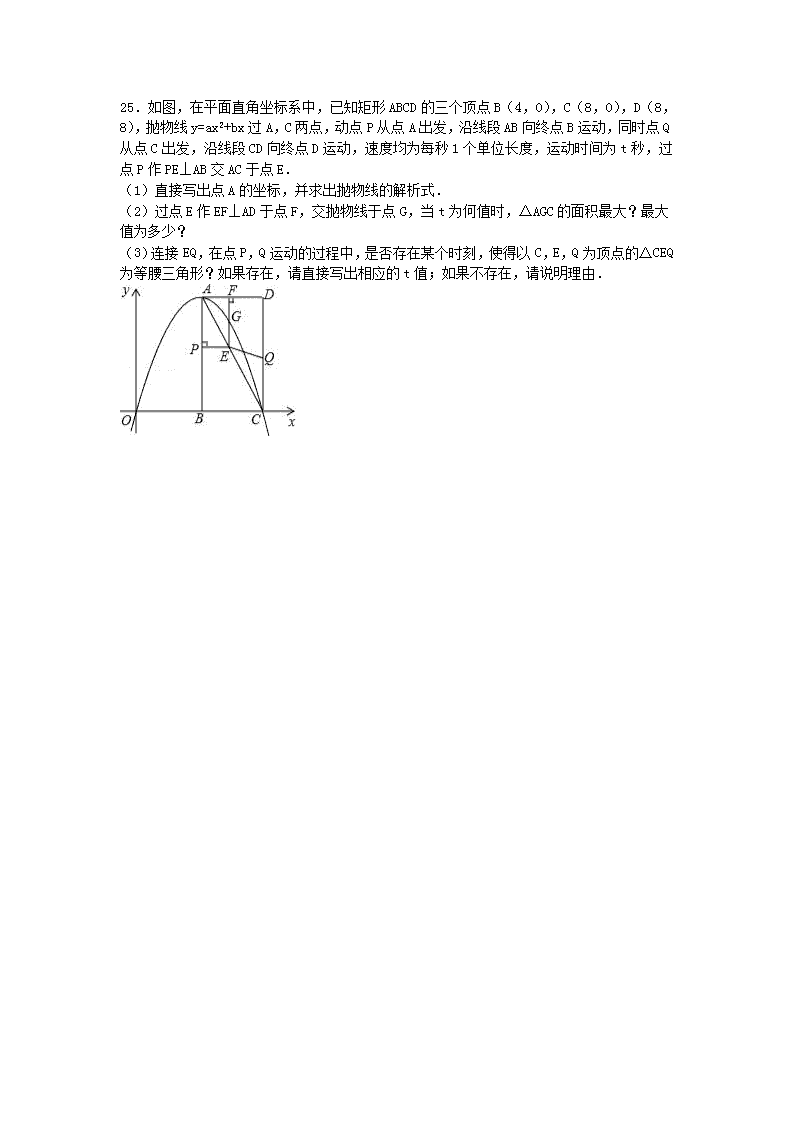
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学一模试卷含解析17
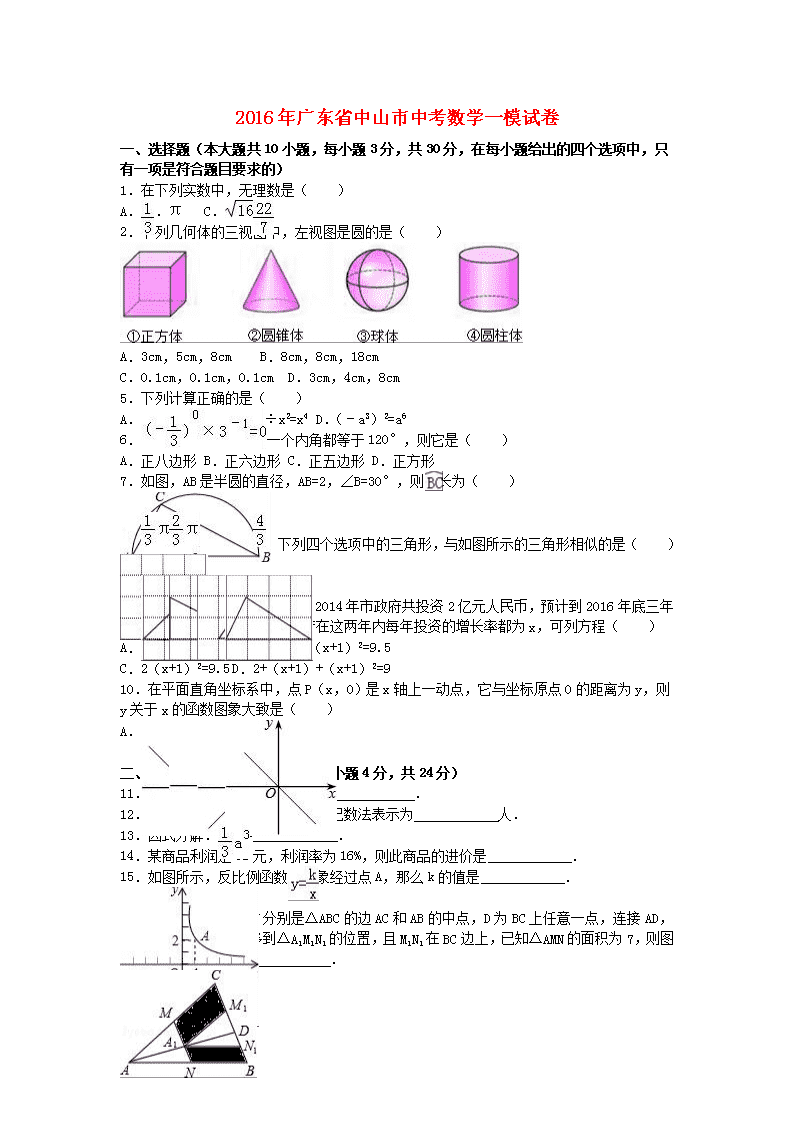
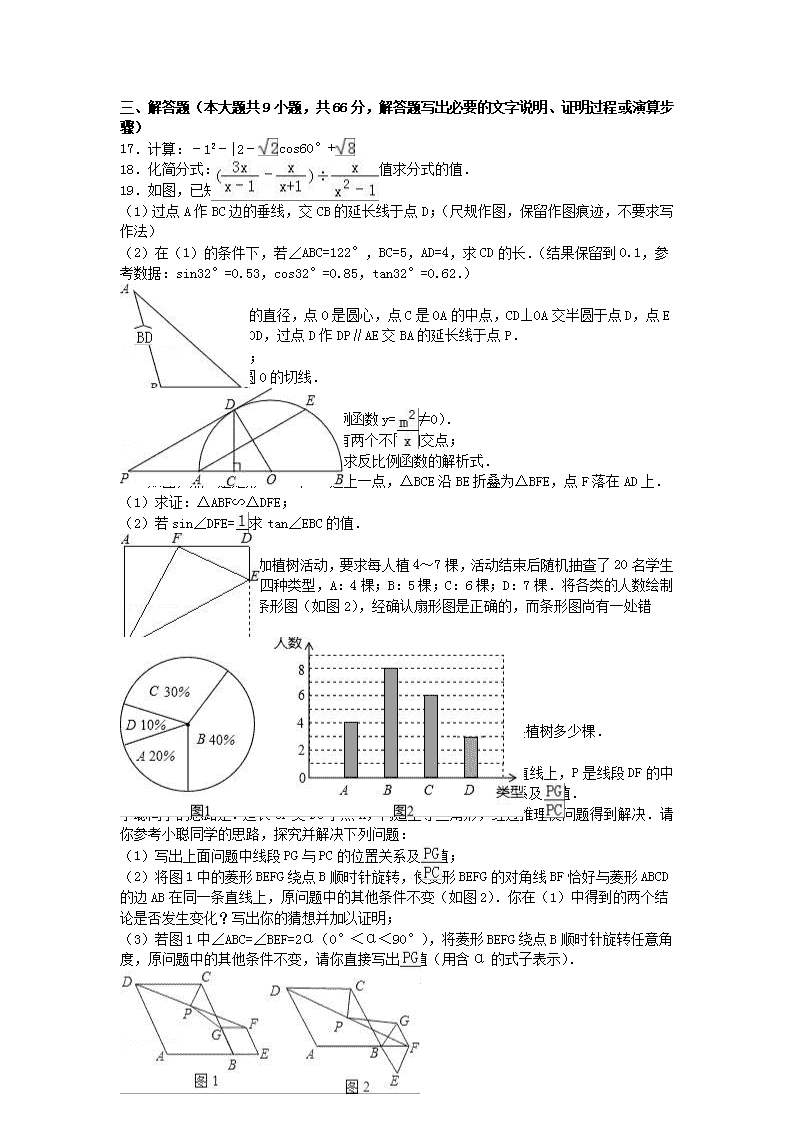
2016年广东省中山市中考数学一模试卷 一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.在下列实数中,无理数是( ) A. B.π C. D. 2.下列几何体的三视图中,左视图是圆的是( ) A.① B.② C.③ D.④ 3.必然事件的概率是( ) A.0 B.0.5 C.1 D.不能确定 4.下列几组线段能组成三角形的是( ) A.3cm,5cm,8cm B.8cm,8cm,18cm C.0.1cm,0.1cm,0.1cm D.3cm,4cm,8cm 5.下列计算正确的是( ) A. B.x5+x5=x10 C.x8÷x2=x4 D.(﹣a3)2=a6 6.若一个正多边形的每一个内角都等于120°,则它是( ) A.正八边形 B.正六边形 C.正五边形 D.正方形 7.如图,AB是半圆的直径,AB=2,∠B=30°,则的长为( ) A. B. C.π D. 8.在小正方形的网格中,下列四个选项中的三角形,与如图所示的三角形相似的是( ) A. B. C. D. 9.某市为了加快城市建设力度.2014年市政府共投资2亿元人民币,预计到2016年底三年共累计投资9.5亿元人民币,若在这两年内每年投资的增长率都为x,可列方程( ) A.2x2=9.5 B.2+2(x+1)+2(x+1)2=9.5 C.2(x+1)2=9.5 D.2+(x+1)+(x+1)2=9 10.在平面直角坐标系中,点P(x,0)是x轴上一动点,它与坐标原点O的距离为y,则y关于x的函数图象大致是( ) A. B. C. D. 二、填空题(本大题共6小题,每小题4分,共24分) 11.不等式4﹣x>1的正整数解为 . 12.我市约有495万人口,用科学记数法表示为 人. 13.因式分解:﹣3a= . 14.某商品利润是32元,利润率为16%,则此商品的进价是 . 15.如图所示,反比例函数的图象经过点A,那么k的值是 . 16.如图,如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置,且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为 . 三、解答题(本大题共9小题,共66分,解答题写出必要的文字说明、证明过程或演算步骤) 17.计算:﹣12﹣|2﹣|+2cos60°+. 18.化简分式:,并选择一个你喜欢的x的值求分式的值. 19.如图,已知钝角△ABC (1)过点A作BC边的垂线,交CB的延长线于点D;(尺规作图,保留作图痕迹,不要求写作法) (2)在(1)的条件下,若∠ABC=122°,BC=5,AD=4,求CD的长.(结果保留到0.1,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.) 20.如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P. (1)求∠AOD的度数; (2)求证:PD是半圆O的切线. 21.已知:一次函数y=x﹣2与反比例函数y=(m≠0). (1)求证:这两个函数的图象一定有两个不同的交点; (2)若他们的一个交点是(1,m),求反比例函数的解析式. 22.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上. (1)求证:△ABF∽△DFE; (2)若sin∠DFE=,求tan∠EBC的值. 23.某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误. 回答下列问题: (1)写出条形图中存在的错误,并说明理由; (2)写出这20名学生每人植树量的众数、中位数; (3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵. 24.请阅读下列材料: 问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及的值. 小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题: (1)写出上面问题中线段PG与PC的位置关系及的值; (2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明; (3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含α的式子表示). 25.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E. (1)直接写出点A的坐标,并求出抛物线的解析式. (2)过点E作EF⊥AD于点F,交抛物线于点G,当t为何值时,△AGC的面积最大?最大值为多少? (3)连接EQ,在点P,Q运动的过程中,是否存在某个时刻,使得以C,E,Q为顶点的△CEQ为等腰三角形?如果存在,请直接写出相应的t值;如果不存在,请说明理由. 2016年广东省中山市中考数学一模试卷 参考答案与试题解析 一、选择题(本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.在下列实数中,无理数是( ) A. B.π C. D. 【考点】无理数. 【分析】初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.由此即可判定选择项. 【解答】解:∵π是无限不循环小数, ∴π是无理数,其它的数都是有理数. 故选B. 2.下列几何体的三视图中,左视图是圆的是( ) A.① B.② C.③ D.④ 【考点】简单几何体的三视图. 【分析】分别找到四个立体图形的左视图即可,左视图是从左面看所得到的平面图形. 【解答】解:①正方体的左视图是正方形; ②圆锥体的左视图是等腰三角形; ③球体的左视图是圆; ④圆柱体的左视图是长方形; 故选:C. 3.必然事件的概率是( ) A.0 B.0.5 C.1 D.不能确定 【考点】概率的意义. 【分析】根据必然事件就是一定发生的事件,即发生的概率是1的事件即可解答. 【解答】解:∵必然事件就是一定发生的事件, ∴必然事件发生的概率是1. 故选:C. 4.下列几组线段能组成三角形的是( ) A.3cm,5cm,8cm B.8cm,8cm,18cm C.0.1cm,0.1cm,0.1cm D.3cm,4cm,8cm 【考点】三角形三边关系. 【分析】利用三角形的三边关系:三角形的任意两边之和>第三边即可判断. 【解答】解:A、3+5=8,不能组成三角形; B、8+8=16<18,不能组成三角形; C、是等边三角形; D、3+4=7<8,不能组成三角形; 故选C. 5.下列计算正确的是( ) A. B.x5+x5=x10 C.x8÷x2=x4 D.(﹣a3)2=a6 【考点】负整数指数幂;合并同类项;幂的乘方与积的乘方;同底数幂的除法;零指数幂. 【分析】根据负整数指数幂、幂的乘方与积的乘方、零指数幂、同底数幂的除法、合并同类项等知识点进行解答. 【解答】解:A、(﹣)0×3﹣1=1×=;故不对; B、x5+x5=2x5;故不对; C、x8÷x2=x6;故不对; D、(﹣a3)2=a6,正确; 故选D. 6.若一个正多边形的每一个内角都等于120°,则它是( ) A.正八边形 B.正六边形 C.正五边形 D.正方形 【考点】多边形内角与外角. 【分析】利用多边形内角和公式,根据性质列出方程即可. 【解答】解:设此多边形变数为x,根据题意,得 (x﹣2)×180=120•x, 解之,得x=6,所以此图形是正六边形. 故选B. 7.如图,AB是半圆的直径,AB=2,∠B=30°,则的长为( ) A. B. C.π D. 【考点】弧长的计算;圆周角定理. 【分析】首先连接CO,再利用圆周角定理计算出圆心角∠COB的度数,然后利用弧长公式进行计算即可. 【解答】解:连接CO, ∵AB=2, ∴OB=1, ∵AB是半圆的直径, ∴∠ACB=90°, ∵∠B=30°, ∴∠A=60°, ∴∠COB=120°, ∴==π, 故选:B. 8.在小正方形的网格中,下列四个选项中的三角形,与如图所示的三角形相似的是( ) A. B. C. D. 【考点】相似三角形的判定;勾股定理. 【分析】根据网格结构以及勾股定理可得所给图形是两直角边分别为、2的直角三角形,然后利用相似三角形的判定方法选择答案即可. 【解答】解:根据勾股定理,所给图形的两直角边为=, =2, 所以,夹直角的两边的比为=, 纵观各选项,只有B选项三角形符合,与所给图形的三角形相似. 故选B. 9.某市为了加快城市建设力度.2014年市政府共投资2亿元人民币,预计到2016年底三年共累计投资9.5亿元人民币,若在这两年内每年投资的增长率都为x,可列方程( ) A.2x2=9.5 B.2+2(x+1)+2(x+1)2=9.5 C.2(x+1)2=9.5 D.2+(x+1)+(x+1)2=9 【考点】由实际问题抽象出一元二次方程. 【分析】设每年市政府投资的增长率为x.根据到2016年底三年共累计投资9.5亿元人民币建设廉租房,列方程求解. 【解答】解:设每年市政府投资的增长率为x, 根据题意,得:2+2(1+x)+2(1+x)2=9.5. 故选:B. 10.在平面直角坐标系中,点P(x,0)是x轴上一动点,它与坐标原点O的距离为y,则y关于x的函数图象大致是( ) A. B. C. D. 【考点】动点问题的函数图象. 【分析】根据x轴上的点到原点的距离是点的横坐标的绝对值,可得答案. 【解答】解:x<0时,y=﹣x,x>0时,y=x. 故选:A. 二、填空题(本大题共6小题,每小题4分,共24分) 11.不等式4﹣x>1的正整数解为 1,2 . 【考点】一元一次不等式的整数解. 【分析】首先利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的正整数即可. 【解答】解:不等式的解集是x<3, 故不等式4﹣x>1的正整数解为1,2. 故答案为1,2. 12.我市约有495万人口,用科学记数法表示为 4.95×106 人. 【考点】科学记数法—表示较大的数. 【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.本题495万=4 950 000有7位整数,n=7﹣1=6. 【解答】解:495万=4 950 000=4.95×106人. 故填4.95×106. 13.因式分解:﹣3a= a(a+3)(a﹣3) . 【考点】提公因式法与公式法的综合运用. 【分析】原式提取公因式,再利用平方差公式分解即可. 【解答】解:原式=a(a2﹣1) =a(a+3)(a﹣3). 故答案为: a(a+3)(a﹣3). 14.某商品利润是32元,利润率为16%,则此商品的进价是 200元 . 【考点】分式方程的应用. 【分析】根据利润=进价×利润率.根据此等量关系列方程得出结果. 【解答】解:设商品的进价是x元, 则16%x=32, x=200元, 答:此商品的进价是200元. 故答案为:200元. 15.如图所示,反比例函数的图象经过点A,那么k的值是 2 . 【考点】反比例函数图象上点的坐标特征. 【分析】根据图示知A(1,2),所以把点A的坐标代入反比例函数解析式,通过方程来求k的值. 【解答】解:如图所示,A(1,2).则 2=, 解得,k=2. 故答案是:2. 16.如图,如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置,且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为 14 . 【考点】平移的性质. 【分析】根据三角形中位线定理得到MN∥BC,MN=BC,得到△AMN∽△ACB,根据相似三角形的性质和平移的性质计算即可. 【解答】解:∵M、N分别是△ABC的边AC和AB的中点, ∴MN∥BC,MN=BC, ∴△AMN∽△ACB,相似比为1:4, ∵△AMN的面积为7, ∴△ABC的面积为28, 由平移的性质可知,△AMN的面积=△A1M1N1的面积=7, ∴图中阴影部分的面积为28﹣7﹣7=14, 故答案为:14. 三、解答题(本大题共9小题,共66分,解答题写出必要的文字说明、证明过程或演算步骤) 17.计算:﹣12﹣|2﹣|+2cos60°+. 【考点】实数的运算;特殊角的三角函数值. 【分析】原式利用乘方的意义,绝对值的代数意义,特殊角的三角函数值,以及二次根式性质计算即可得到结果. 【解答】解:原式=﹣1﹣2++2×+2 =﹣2+3. 18.化简分式:,并选择一个你喜欢的x的值求分式的值. 【考点】分式的化简求值. 【分析】这是个分式除法与减法混合运算题,运算顺序是先做括号内的减法,此时要先确定最简公分母进行通分;做除法时要注意先把除法运算转化为乘法运算,而做乘法运算时要注意先把分子、分母能因式分解的先分解,然后约分.x取不为±1、0的任何数. 【解答】解: =×=2x+4,取x=2,原式=8. 19.如图,已知钝角△ABC (1)过点A作BC边的垂线,交CB的延长线于点D;(尺规作图,保留作图痕迹,不要求写作法) (2)在(1)的条件下,若∠ABC=122°,BC=5,AD=4,求CD的长.(结果保留到0.1,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.) 【考点】作图—基本作图;解直角三角形. 【分析】(1)利用基本作图:过直线外一点作直线的垂线作出垂线段AD即可; (2)根据三角形外角的性质求出∠DAB的度数,在Rt△ADB中,利用锐角三角函数的定义求出DB的长,进而可得出结论. 【解答】解:(1)如图所示; (2)∵∠ABC=122°,∠D=90°, ∴∠DAB=32°. 在Rt△ADB中, ∵tan∠DAB=,即0.62=, ∴DB=2.48, ∴DC=2.48+5=7.48≈7.5. 20.如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P. (1)求∠AOD的度数; (2)求证:PD是半圆O的切线. 【考点】垂径定理;平行线的性质;圆周角定理;切线的判定. 【分析】(1)根据CO与DO的数量关系,即可得出∠CDO的度数,进而求出∠AOD的度数; (2)利用点E是的中点,进而求出∠EAB=30°,即可得出∠AFO=90°,即可得出答案. 【解答】(1)解:∵AB是半圆的直径,点O是圆心,点C是OA的中点, ∴2CO=DO,∠DCO=90°, ∴∠CDO=30°, ∴∠AOD=60°; (2)证明:如图,连接OE, ∵点E是的中点, ∴=, ∵由(1)得∠AOD=60°, ∴∠DOB=120°, ∴∠BOE=60°, ∴∠EAB=30°, ∴∠AFO=90°, ∵DP∥AE, ∴PD⊥OD, ∴直线PD为⊙O的切线. 21.已知:一次函数y=x﹣2与反比例函数y=(m≠0). (1)求证:这两个函数的图象一定有两个不同的交点; (2)若他们的一个交点是(1,m),求反比例函数的解析式. 【考点】反比例函数与一次函数的交点问题. 【分析】(1)将两个函数解析式联立后,通过方程x2﹣2x﹣m2=0的判别式判断方程总有两个不相等的实数根,再进行证明; (2)将点A分别代入两个函数解析式,继而即可求出m的值. 【解答】解:(1)证明:把y=x﹣2代入y=得x﹣2=, 整理得:x2﹣2x﹣m2=0, ∵△=4+4m2,且m≠0, ∴4+4m2>0, ∴方程x2﹣2x﹣m2=0有两个不相等的实数根, ∴这两个函数的图象一定有两个不同的交点; (2)把x=1,y=m代入y=x﹣2得,m=﹣1, 故反比例函数的解析式为y=. 22.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上. (1)求证:△ABF∽△DFE; (2)若sin∠DFE=,求tan∠EBC的值. 【考点】相似三角形的判定与性质;矩形的性质;翻折变换(折叠问题);解直角三角形. 【分析】(1)根据矩形的性质可知∠A=∠D=∠C=90°,△BCE沿BE折叠为△BFE,得出∠BFE=∠C=90°,再根据三角形的内角和为180°,可知∠AFB+∠ABF=90°,得出∠ABF=∠DFE,即可证明△ABF∽△DFE, (2)已知sin∠DFE=,设DE=a,EF=3a,DF==2a,可得出CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF,由(1)中△ABF∽△DFE,可得tan∠EBC=tan∠EBF==. 【解答】(1)证明:∵四边形ABCD是矩形 ∴∠A=∠D=∠C=90°, ∵△BCE沿BE折叠为△BFE, ∴∠BFE=∠C=90°, ∴∠AFB+∠DFE=180°﹣∠BFE=90°, 又∵∠AFB+∠ABF=90°, ∴∠ABF=∠DFE, ∴△ABF∽△DFE, (2)解:在Rt△DEF中,sin∠DFE==, ∴设DE=a,EF=3a,DF==2a, ∵△BCE沿BE折叠为△BFE, ∴CE=EF=3a,CD=DE+CE=4a,AB=4a,∠EBC=∠EBF, 又由(1)△ABF∽△DFE, ∴===, ∴tan∠EBF==, tan∠EBC=tan∠EBF=. 23.某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误. 回答下列问题: (1)写出条形图中存在的错误,并说明理由; (2)写出这20名学生每人植树量的众数、中位数; (3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵. 【考点】众数;用样本估计总体;扇形统计图;条形统计图;中位数. 【分析】(1)利用总人数20乘以对应的百分比即可求得D类的人数解答; (2)根据众数、中位数的定义即可直接求解; (3)首先求得调查的20人的平均数,乘以总人数260即可. 【解答】解(1)D错误,理由为:20×10%=2≠3(人). (2)众数为5棵,中位数为5棵 (3)==5.3(棵). 估计260名学生共植树5.3×260=1378(棵). 24.请阅读下列材料: 问题:如图1,在菱形ABCD和菱形BEFG中,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,探究PG与PC的位置关系及的值. 小聪同学的思路是:延长GP交DC于点H,构造全等三角形,经过推理使问题得到解决.请你参考小聪同学的思路,探究并解决下列问题: (1)写出上面问题中线段PG与PC的位置关系及的值; (2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明; (3)若图1中∠ABC=∠BEF=2α(0°<α<90°),将菱形BEFG绕点B顺时针旋转任意角度,原问题中的其他条件不变,请你直接写出的值(用含α的式子表示). 【考点】菱形的性质;全等三角形的判定与性质;锐角三角函数的定义. 【分析】(1)根据题意可知小聪的思路为,通过判定三角形DHP和PGF为全等三角形来得出证明三角形HCG为等腰三角形且P为底边中点的条件; (2)思路同上,延长GP交AD于点H,连接CH,CG,本题中除了如(1)中证明△GFP≌△HDP(得到P是HG中点)外还需证明△HDC≌△GBC(得出三角形CHG是等腰三角形). (3)∠ABC=∠BEF=2α(0°<α<90°),那么∠PCG=90°﹣α,由(1)可知:PG:PC=tan(90°﹣α). 【解答】解:(1)∵CD∥GF,∠PDH=∠PFG,∠DHP=∠PGF,DP=PF, ∴△DPH≌△FGP, ∴PH=PG,DH=GF, ∵CD=BC,GF=GB=DH, ∴CH=CG, ∴CP⊥HG,∠ABC=60°, ∴∠DCG=120°, ∴∠PCG=60°, ∴PG:PC=tan60°=, ∴线段PG与PC的位置关系是PG⊥PC, =; (2)猜想:(1)中的结论没有发生变化. 证明:如图2,延长GP交AD于点H,连接CH, ∵P是线段DF的中点, ∴FP=DP, ∵AD∥GF, ∴∠HDP=∠GFP, ∵∠GPF=∠HPD, ∴△GFP≌△HDP(ASA), ∴GP=HP,GF=HD, ∵四边形ABCD是菱形, ∴CD=CB,∠HDC=∠ABC=60°, ∵∠ABC=∠BEF=60°,菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上, ∴∠GBF=60°, ∴∠HDC=∠GBF, ∵四边形BEFG是菱形, ∴GF=GB, ∴HD=GB, ∴△HDC≌△GBC, ∴CH=CG,∠HCD=∠GCB ∴PG⊥PC(到线段两端点距离相等的点在线段的垂直平分线上) ∵∠ABC=60° ∴∠DCB=∠HCD+∠HCB=120° ∵∠HCG=∠HCB+∠GCB ∴∠HCG=120° ∴∠GCP=60° ∴=tan∠GCP=tan60°=; (3)∵∠ABC=∠BEF=2α(0°<α<90°), ∴∠PCG=90°﹣α, 由(1)可知:PG:PC=tan(90°﹣α), ∴=tan(90°﹣α). 25.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0),C(8,0),D(8,8),抛物线y=ax2+bx过A,C两点,动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒,过点P作PE⊥AB交AC于点E. (1)直接写出点A的坐标,并求出抛物线的解析式. (2)过点E作EF⊥AD于点F,交抛物线于点G,当t为何值时,△AGC的面积最大?最大值为多少? (3)连接EQ,在点P,Q运动的过程中,是否存在某个时刻,使得以C,E,Q为顶点的△CEQ为等腰三角形?如果存在,请直接写出相应的t值;如果不存在,请说明理由. 【考点】二次函数综合题. 【分析】(1)由于四边形ABCD为矩形,所以A点与D点纵坐标相同,A点与B点横坐标相同; (2)根据相似三角形的性质,可得PE、PB的长,可得E点坐标,根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得GE的长,根据三角形的面积公式,可得二次函数,根据二次函数的性质,可得答案; (3)若构成等腰三角形,则三条边中有两条边相等即可,于是可分EQ=QC,EC=CQ,EQ=EC三种情况讨论.若有两种情况时间相同,则三边长度相同,为等腰三角形. 【解答】解:(1)因为点B的横坐标为4,点D的纵坐标为8,AD∥x轴,AB∥y轴,所以点A的坐标为(4,8). 将A(4,8)、C(8,0)两点坐标分别代入y=ax2+bx得, 解得. 故抛物线的解析式为:y=﹣x2+4x; (2)∵PE∥BC,∴△APE∽△ABC, =,即=,PE=AP=t,PB=8﹣t, E(4+t,8﹣t),G点的坐标为(4+t,﹣t2+8), GE=(﹣t2+8)﹣(8﹣t)=﹣t2+t, S△AGC=GE•(xC﹣xA)=(﹣t2+t)(8﹣4)=﹣(t﹣4)2+4, 当t=4时,△AGC的面积最大,最大值为4; (3)①当EQ=QC时,∵Q(8,t),E(4+t,8﹣t),QC=t, 所以根据两点间距离公式,得: (t﹣4)2+(8﹣2t)2=t2. 整理得13t2﹣144t+320=0, 解得t=或t==8(此时E、C重合,不能构成三角形,舍去). ②当EC=CQ时, 因为E(4+t,8﹣t),C(8,0),QC=t, 所以根据两点间距离公式,得: (4+t﹣8)2+(8﹣t)2=t2. 整理得t2﹣80t+320=0,t=40﹣16,t=40+16>8(此时Q不在矩形的边上,舍去). ③当EQ=EC时, 因为Q(8,t),E(4+t,8﹣t),C(8,0), 所以根据两点间距离公式,得:(t﹣4)2+(8﹣2t)2=(4+t﹣8)2+(8﹣t)2, 解得t=0(此时Q、C重合,不能构成三角形,舍去)或t=. 于是t1=,t2=,t3=40﹣16.查看更多