中考复习之专题八三角形完美编辑版

中考复习之专题八三角形完美编辑版

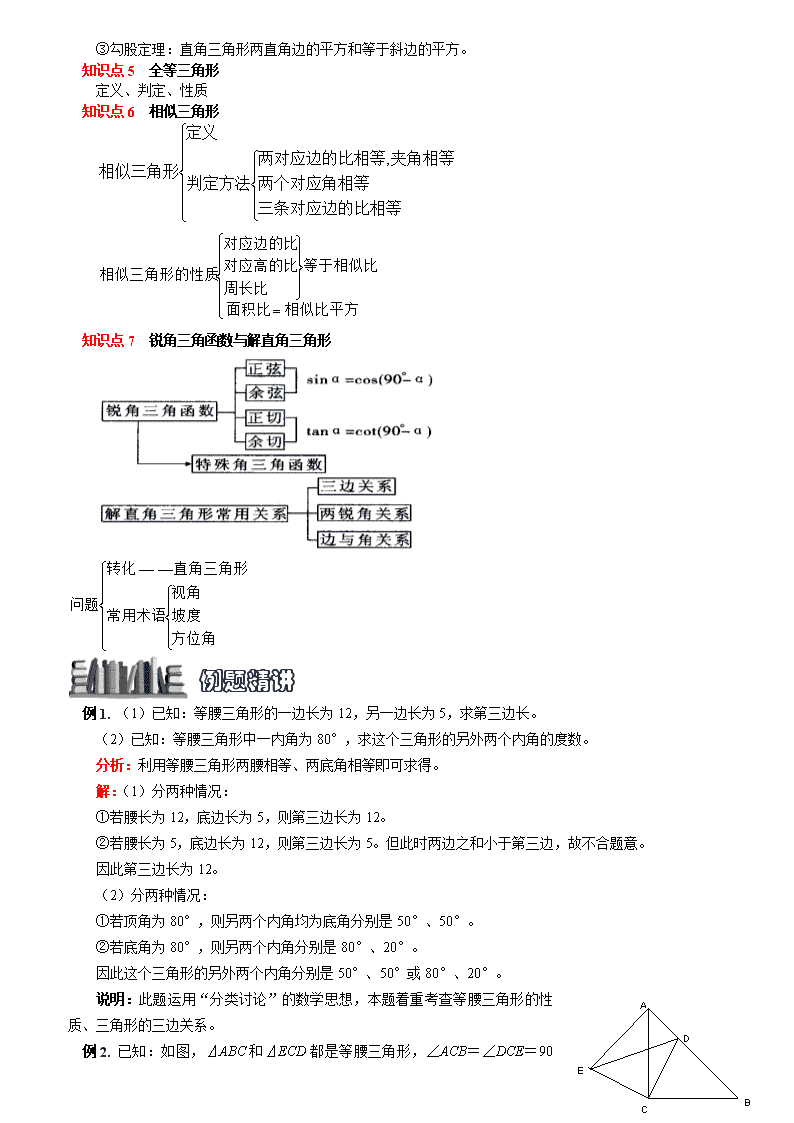
中考复习之专题八 三角形、三角形的相似及全等、解直角三角形 教学准备 一. 教学目标：‎ ‎（1）掌握三角形、三角形的全等、相似及解直角三角形的有关概念。‎ ‎（2）利用三角形的相似、全等及解直角三角形的知识进行计算、解答有关综合题。‎ ‎（3）培养学生的转化、数形结合、及分类讨论的数学思想的能力 二. 教学重点、难点：‎ 三角形、三角形的相似及全等、解直角三角形的基础知识、基本技能是本节的重点。难点是综合应用这些知识解决问题的能力。‎ 三. 知识要点：‎ 知识点1 三角形的边、角关系 ‎①三角形任何两边之和大于第三边；‎ ‎②三角形任何两边之差小于第三边；‎ ‎③三角形三个内角的和等于180°；‎ ‎④三角形三个外角的和等于360°；‎ ‎⑤三角形一个外角等于和它不相邻的两个内角的和；‎ ‎⑥三角形一个外角大于任何一个和它不相邻的内角。‎ 知识点2 三角形的主要线段和外心、内心 ‎①三角形的角平分线、中线、高；‎ ‎②三角形三边的垂直平分线交于一点，这个点叫做三角形的外心，三角形的外心到各顶点的距离相等；‎ ‎③三角形的三条角平分线交于一点，这个点叫做三角形的内心，三角形的内心到三边的距离相等；‎ ‎④连结三角形两边中点的线段叫做三角形的中位线，三角形的中位线平行于第三边且等于第三边的一半。‎ 知识点3 等腰三角形 等腰三角形的识别：‎ ‎①有两边相等的三角形是等腰三角形；‎ ‎②有两角相等的三角形是等腰三角形（等角对等边）；‎ ‎③三边相等的三角形是等边三角形；‎ ‎④三个角都相等的三角形是等边三角形；‎ ‎⑤有一个角是60°的等腰三角形是等边三角形。‎ 等腰三角形的性质：‎ ‎①等边对等角；‎ ‎②等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合；‎ ‎③等腰三角形是轴对称图形，底边的中垂线是它的对称轴；‎ ‎④等边三角形的三个内角都等于60°。‎ 知识点4 直角三角形 直角三角形的识别：‎ ‎①有一个角等于90°的三角形是直角三角形；‎ ‎②有两个角互余的三角形是直角三角形；‎ ‎③勾股定理的逆定理：如果一个三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。‎ 直角三角形的性质：‎ ‎①直角三角形的两个锐角互余；‎ ‎②直角三角形斜边上的中线等于斜边的一半；‎ ‎③勾股定理：直角三角形两直角边的平方和等于斜边的平方。‎ 知识点5 全等三角形 定义、判定、性质 知识点6 相似三角形 知识点7 锐角三角函数与解直角三角形 例题精讲 例1. （1）已知：等腰三角形的一边长为12，另一边长为5，求第三边长。‎ ‎（2）已知：等腰三角形中一内角为80°，求这个三角形的另外两个内角的度数。‎ 分析：利用等腰三角形两腰相等、两底角相等即可求得。‎ 解：（1）分两种情况：‎ ‎①若腰长为12，底边长为5，则第三边长为12。‎ ‎②若腰长为5，底边长为12，则第三边长为5。但此时两边之和小于第三边，故不合题意。‎ 因此第三边长为12。‎ ‎（2）分两种情况：‎ ‎①若顶角为80°，则另两个内角均为底角分别是50°、50°。‎ ‎②若底角为80°，则另两个内角分别是80°、20°。‎ 因此这个三角形的另外两个内角分别是50°、50°或80°、20°。‎ 说明：此题运用“分类讨论”的数学思想，本题着重考查等腰三角形的性质、三角形的三边关系。‎ 例2. 已知：如图，⊿ABC和⊿ECD都是等腰三角形，∠ACB＝∠DCE＝90‎ ‎°，D为AB边上的一点，求证：（1）⊿ACE≌⊿BCD，（2）AD＋AE＝DE。‎ 分析：要证⊿ACE≌⊿BCD，已具备AC＝BC，CE＝CD两个条件，还需AE＝BD或∠ACE＝∠BCD，而∠ACE＝∠BCD显然能证;要证AD＋AE＝DE，需条件∠DAE＝90°，因为∠BAC＝45°，所以只需证∠CAE＝∠B＝45°，由⊿ACE≌⊿BCD能得证。‎ 证明：（1）∵∠DCE＝∠ACB＝90°，∴∠DCE－∠ACD＝∠ACB－∠ACD，‎ 即∠ACE＝∠BCD，∵AC＝BC，CE＝CD，‎ ‎∴⊿ACE≌⊿BCD。‎ ‎（2）∵⊿ACE≌⊿BCD，∴∠CAE＝∠B＝45°，∵∠BAC＝∠B＝45°，∴∠DAE＝90°，∴AD＋AE＝DE。‎ 例3. 已知：点P是等边⊿ABC内的一点，∠BPC＝150°，PB＝2，PC＝3，求PA的长。‎ 分析：将⊿BAP绕点B顺时针方向旋转60°至⊿BCD，即可证得⊿BPD为等边三角形，⊿PCD为直角三角形。‎ 解：∵BC＝BA，‎ ‎∴将⊿BAP绕点B顺时针方向旋转60°，使BA与BC重合，得⊿BCD，连结PD。‎ ‎∴BD＝BP＝2，PA＝DC。∴⊿BPD是等边三角形。∴∠BPD＝60°。‎ ‎∴∠DPC＝∠BPC－∠BPD＝150°－60°＝90°。‎ ‎∴DC＝．∴PA＝DC＝。‎ ‎【变式】若已知点P是等边⊿ABC内的一点，PA＝，PB＝2，PC＝3。能求出∠BPC的度数吗？请试一试。‎ 例4. 如图，P是等边三角形ABC内的一点，连结PA、PB、PC，以BP为边作∠PBQ＝60°，且BQ＝BP，连结CQ．‎ ‎（1）观察并猜想AP与CQ之间的大小关系，并证明你的结论．‎ ‎（2）若PA：PB：PC＝3：4：5，连结PQ，试判断△PQC的形状，并说明理由．‎ 解：（1）把△ABP绕点B顺时针旋转60°即可得到△CBQ．利用等边三角形的性质证△ABP≌△CBQ，得到AP＝CQ．‎ ‎（2）连接PQ，则△PBQ是等边三角形．PQ＝PB，AP＝CQ故CQ：PQ：PC＝PA：PB：PC＝3：4：5，∴△PQC是直角三角形．‎ ‎ 点评：利用等边三角形性质、判定、三角形全等、直角三角形的判定等知识点完成此题的证明．‎ 例5. 如图，有两个长度相同的滑梯（即BC＝EF），左边滑梯的高度AC 与右边滑梯水平方向的长度DF相等，则∠ABC＋∠DFE＝______．‎ ‎ 分析：∠ABC与∠DFE分布在两个直角三角形中，若说明这两个直角三角形全等则问题便会迎刃而解．‎ 解答：在Rt△ABC和Rt△DEF中，BC＝EF，AC＝DF，‎ ‎∴△ABC≌△DEF，∴∠ABC＝∠DEF，‎ ‎∴∠ABC＋∠DFE＝90°，因此填90°．‎ ‎ 点评：此例主要依据用所探索的直角三角形全等的条件来识别两个直角三角形全等，并运用与它相关的性质进行解题．‎ 例6. 《中华人民共和国道路交通管理条例》规定：“小汽车在城市街道上的行驶速度不得超过70千米/时”．一辆小汽车在一条城市街道上由西向东行驶（如图所示），在距离路边25米处有“车速检测仪O”，测得该车从北偏西60°的A点行驶到北偏西30°的B点，所用时间为1.5秒．‎ ‎（1）试求该车从A点到B的平均速度；（2）试说明该车是否超过限速．‎ 解析：（1）要求该车从A点到B点的速度．只需求出AB的距离，‎ 在△OAC中，OC＝25米．∵∠OAC＝90°－60°＝30°，∴OA＝2CO＝50米 ‎ 由勾股定理得CA＝＝25（米）‎ ‎ 在△OBC中，∠BOC＝30°‎ ‎ ∴BC＝OB。 ∴（2BC）2＝BC2＋252 ∴BC＝（米）‎ ‎ ∴AB＝AC－BC＝25－＝（米）∴从A到B的速度为÷1.5＝（米/秒）‎ ‎ （2）米/秒≈69.3千米/时 ‎ ∵69.3千米/时<70千米/时 ‎ ∴该车没有超过限速． 点评：此题应用了直角三角形中30°角对的直角边是斜边的一半及勾股定理，也是几何与代数的综合应用．‎ 例7. 如图，正方形网格中，小格的顶点叫做格点，小华按下列要求作图：①在正方形网格的三条不同的实线上各取一个格点，使其中任意两点不在同一实线上；②连结三个格点，使之构成直角三角形，小华在下面的正方形网格中作出了Rt△ABC．请你按照同样的要求，在右边的两个正方形网格中各画出一个直角三角形，并使三个网格中的直角三角形互不全等．‎ ‎ 简析：此题的答案可以有很多种，关键是抓住有一直角这一特征，可以根据勾股定理的逆定理“若两边的平方和等于第三边的平方，则三角形为直角三角形”构造出直角三角形，答案如下图．‎ 例8. 如图所示，在△ABC中，AB＝AC＝1，点D、E在直线BC上运动，设BD＝x，CE＝y．‎ ‎（1）如果∠BAC＝30°，∠DAE＝105°，试确定y与x之间的函数关系式；‎ ‎（2）如果∠BAC的度数为α，∠DAE的度数为β，当α、β满足怎样的关系式时，（1）中y与x之间的函数关系式还成立，试说明理由．‎ 解：（1）在△ABC中，AB＝AC＝1，∠BAC＝30°，∠ABC＝∠ACB＝75°，∠ABD＝∠ACE＝105°．‎ 又∠DAE＝105°，∴∠DAB＋∠CAE＝75°．‎ 又∠DAB＋∠ADB＝∠ABC＝75°，‎ ‎∴∠CAE＝∠ADB，∴△ADB∽△EAC，‎ ‎∴，∴y＝．‎ ‎（2）当α、β满足β－ ＝90°，y＝仍成立．‎ 此时∠DAB＋∠CAE＝β－α，∴∠DAB＋∠ADB＝β－α，‎ ‎∴∠CAE＝∠ADB．‎ 又∵∠ABD＝∠ACE，∴△ADB∽△EAC，∴y＝．‎ 点评：确定两线段间的函数关系，可利用线段成比例、找相等关系转化为函数关系．‎ 例9. 如图，梯形ABCD中，AB∥CD，且AB＝2CD，E，F分别是AB，BC的中点，EF与BD相交于点M．‎ ‎（1）求证：△EDM∽△FBM；‎ ‎（2）若DB＝9，求BM．‎ ‎（1）证明：∵E是AB中点，∴AB＝2BE，AB＝2CD，∴CD＝EB，‎ 又AB∥CD，∴四边形CBED是平行四边形，‎ ‎∴CB∥DE，∴，∴△EDM∽△FBM． ‎ ‎（2）解：△EDM∽△FBM，∴，‎ ‎∴F是BC中点，DE＝2FB，∴DM＝2BM，∴BM＝DB＝3 ‎ 例10. 已知△ABC中，∠ACB＝90º，CD⊥AB于D，AD∶BD＝2∶3且CD＝6。‎ 求（1）AB；（2）AC。‎ 分析：设AD＝2k，BD＝3k。根据直角三角形和它斜边上的高，可知△ABC∽△ACD∽△CBD。通过相似三角形对应边成比例求出其中k的大小；但是如果根据射影定理，那么就可以直接计算出k的大小。‎ 解：设AD＝2k，BD＝3k（k >0）。‎ ‎∵∠ACB＝90º，CD⊥AB。∴CD2＝AD•BD，‎ ‎∴62＝2k•3k，∴k＝。∴AB＝。又∵AC2＝AD•AB，∴AC＝。‎ 例11. 已知△ABC中，∠ACB＝90º，CH⊥AB，HE⊥BC，HF⊥AC。‎ 求证：（1）△HEF ≌△EHC；（2）△HEF∽△HBC。‎ 分析：从已知条件中可以获得四边形CEHF是矩形，要证明三角形全等要收集到三个条件，有公共边EH，根据矩形的性质可知EF＝CH，HF＝EC。‎ 要证明三角形相似，从条件中得∠FHE＝∠CHB＝90º，由全等三角形可知，∠HEF＝∠HCB，这样就可以证明两个三角形相似。‎ 证明：∵HE⊥BC，HF⊥AC，‎ ‎∴∠CEH＝∠CFH＝90º。又∵∠ACB＝90º，∴四边形CEHF是矩形。‎ ‎∴EF＝CH，HF＝EC，∠FHE＝90º。‎ 又∵HE＝EH，‎ ‎∴△HFE ≌△EHC。∴∠HEF＝∠HCB。‎ ‎∵∠FHE＝∠CHB＝90º，‎ ‎∴△HEF∽△HBC。‎ 说明：在这一题的分析过程中，走“两头凑”比较快捷，从已知出发，发现有用的信息，从结论出发，寻找解决问题需要的条件。解题中还要注意上下两小题的“台阶”关系。培养学生良好的思维习惯。‎ 例12. 两个全等的含30º，60º角的三角板ADE和ABC如图所示放置，E，A，C三点在一条直线上，连接BD，取BD的中点M，连结ME，MC。试判断△EMC是什么样的三角形，并说明理由。‎ 分析：判断一个三角形的形状，可以结合所给出的图形作出假设，或许是等腰三角形。这样就可以转化为另一个问题：尝试去证明EM＝MC，要证线段相等可以寻找全等三角形来解决，然而图中没有形状大小一样的两个三角形。这时思考的问题就可以转化为这样一个新问题：如何构造一对全等三角形？根据已知点M是直角三角形斜边的中点，产生联想：直角三角形斜边上的中点是斜边的一半，得：MD＝MB＝MA。连结M A后，可以证明△MDE≌△MAC。‎ 答：△EMC是等腰直角三角形。‎ 证明：连接AM，由题意得，‎ DE＝AC，AD＝AB，∠DAE＋∠BAC＝90º。∴∠DAB＝90º。‎ ‎∴△DAB为等腰直角三角形。‎ 又∵MD＝MB，‎ ‎∴MA＝MD＝MB，AM⊥DB，∠MAD＝∠M AB＝45º。‎ ‎∴∠MDE＝∠MAC＝105º，∠DMA＝90º。‎ ‎∴△MDE≌△MAC。‎ ‎∴∠DME＝∠AMC，ME＝MC。‎ 又∠DME＋∠EMA＝90º，‎ ‎∴∠AMC＋∠EMA＝90º。‎ ‎∴MC⊥EM。‎ ‎∴△EMC是等腰直角三角形。‎ 说明：构造全等三角形是解决这个问题的关键，那么构造全等又如何进行的呢？对条件的充分认识和对知识点的联想可以找到添加辅助线的途径。构造过程中要不断地转化问题或转化思维的角度。会转化，善于转化，更能体现思维的灵活性。在问题中创设以三角板为情境也是考题的一个热点。‎ 课后练习 ‎1. 如图，△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列三个条件：①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD．‎ ‎（1）上述三个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出所有情形）； （2）选择第（1）小题中的一种情况，证明△ABC是等腰三角形．‎ ‎2. （1）已知如图①，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝60º。‎ 求证：①AC＝BD，②∠APB＝60º。‎ ‎（2）如图②，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，则AC与BD间的等量关系式为______________；∠APB的大小为_____________。‎ ‎（3）如图③，在△AOB和△COD中，OA＝kOB，OC＝kOD（k>1），∠AOB＝∠COD＝α，则AC与BD间的等量关系式为_________________；∠APB的大小为_____________。‎ ‎ 3. 一块直角三角形木板的一条直角边AB长为‎1.5m，面积为‎1.5m2‎ ‎，工人师傅要把它加工成一个面积最大的正方形，请两位同学设计加工方案，甲设计方案如图（1），乙设计的方案如图（2）。你认为哪位同学设计的方案较好？试说明理由。（加工损耗忽略，计算结果可保留分数）‎ ‎4. 一般的室外放映的电影胶片上每一个图片的规格为：‎3.5cm×‎3.5cm，放映的荧屏的规格为‎2m×‎2m，若放映机的光源距胶片‎20cm时，问荧屏应拉在离镜头多远的地方，放映的图象刚好布满整个荧屏？‎ ‎5. 如图，已知∠MON＝90º，等边三角形ABC的一个顶点A是射线OM上的一定点，顶点B与点O重合，顶点C在∠MON内部。‎ ‎（1）当顶点B在射线ON上移动到B1时，连结AB1为一边的等边三角形AB1C1（保留作图痕迹，不写作法和证明）； ‎ ‎（2）设AB1与OC交于点Q，AC的延长线与B1C1交于点D。求证：；‎ ‎（3）连结CC1，试猜想∠ACC1为多少度？并证明你的猜想。‎ ‎6. 如图所示，设A城气象台测得台风中心在A城正西方向‎600km的B处，正以每小时‎200km的速度沿北偏东60°的BF方向移动，距台风中心‎500km的范围是受台风影响的区域．‎ ‎ （1）A城是否受到这次台风的影响？为什么？‎ ‎（2）若A城受到这次台风的影响，那么A城遭受这次台风的影响有多长时间？‎ ‎7. （1）如图，在Rt△ABC中，∠C＝90°，AD是∠BAC的角平分线，∠CAB＝60°，CD＝，BD＝‎ ‎2，求AC，AB的长．‎ ‎（2）“实验中学”有一块三角形状的花园ABC，有人已经测出∠A＝30°，AC＝40米，BC＝25米，你能求出这块花园的面积吗？‎ ‎（3）某片绿地形状如图所示，其中AB⊥BC，CD⊥AD，∠A＝60°，AB＝200m，CD＝100m，求AD、BC的长．‎ ‎8. 高为‎12米的教学楼ED前有一棵大树AB，如图所示．‎ ‎ （1）某一时刻测得大树AB，教学楼ED在阳光下的投影长分别是BC＝‎2.5米，DF＝‎7.5米，求大树AB的高度；‎ ‎ （2）现有皮尺和高为h米的测角仪，请你设计另一种测量大树AB高度的方案，要求：‎ ‎ ①在图中，画出你设计的图形（长度用字母m，n……表示，角度用希腊字母α，β……表示）；‎ ‎ ②根据你所画出的示意图和标注的数据，求出大树的高度并用字母表示．‎ ‎9. 如图所示，某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高‎6米的小区超市，超市以上是居民住房，在该楼的前面15米处要盖一栋高‎20米的新楼．当冬季正午的阳光与水平线的夹角为32°时．‎ ‎（1）问超市以上的居民住房采光是否受影响，为什么？‎ ‎（2）若要使超市采光不受影响，两楼至少应相距多少米？（结果保留整数，参考数据：sin32°≈，cos32°≈．）‎ 练习答案 ‎1. 解：（1）①③或②③ ‎ ‎（2）已知①③求证△ABC是等腰三角形．‎ 证：先证△EBO≌△DCO．得OB＝OC，得∠DBC＝∠ECB．‎ ‎∴∠ABC＝∠ACB．即△ABC是等腰三角形 ‎2. 证明：∵△AOB和△COD为正三角形，‎ ‎∴OA＝OB，OD＝OC，∠AOB＝60º，∠COD＝60º。‎ ‎∵∠AOB＋∠BOC＝∠COD＋∠BOC，∴∠AOC＝∠BOD。‎ ‎∴△AOC≌△BOD ，∴AC＝BD。∴∠OAC＝∠OBD，‎ ‎∴∠APB＝∠AOB＝60º。‎ ‎（2）AC与BD间的等量关系式为AC＝BD；∠APB的大小为α。‎ ‎（3）AC与BD间的等量关系式为AC＝kBD；∠APB的大小为180º－α。‎ ‎3. 解：方案（1）：有题意可知，DE∥BA，‎ 得△CDE∽△CBA。∴；‎ 方案（2）：作BH⊥AC于H。DE∥AC，得△BDE∽△BAC。‎ ‎∴。∵∴图（1）加工出的正方形面积大。‎ 综上所得，甲同学设计的方案较好。‎ ‎4. 解：胶片上的图象和荧屏上的图象是位似的，镜头就相当于位似中心，因此本题可以转化为位似问题解答．：m ‎5. 解：（1）如图所示；‎ 证明：（2）∵△AOC与△AB1C1是等边三角形，‎ ‎∴∠ACB＝∠AB1D＝60º。‎ 又∵∠CAQ＝∠B1AD，∴△ACQ∽△AB1D；‎ ‎（3）猜想∠ACC1＝90º。‎ 证明：∵△AOC和△AB1C1为正三角形，AO＝AC，AB1＝AC1，‎ ‎∴∠OAC＝∠C1AB1，‎ ‎∴∠OAC－∠CAQ＝∠C1AB1－∠CAQ，∴∠OAB1＝∠CAC1。∴△AO B1 ≌ △AC C1。‎ ‎∴∠ACC1＝∠AOB1＝90º。‎ ‎6. （1）作AM⊥BF可计算AM＝‎300km<‎500km，故A城受影响 ‎ ‎（2）受影响时间为小时 ‎7. 解：（1）AC＝3，AB＝6 ‎ ‎（2）能，分两种情况，S△ABC＝200－150和S△ABC＝200＋150 ‎ ‎ ‎ ‎（3）延长BC，AD交于E，AD＝400－100，BC＝200－200．‎ ‎8. 解：连结AC，EF，‎ ‎（1）∵太阳光线是平行的，‎ ‎∴AC∥EF，∠ACB＝∠EFD，‎ ‎∵∠ABC＝∠EDF＝90°，‎ ‎∴△ABC∽△EDF，∴，‎ ‎∴AB＝4米 ‎ ‎（2）①如图所示：‎ ‎②AB＝（mtanα＋h）米．‎ ‎9. 解：（1）超市以上居民住房采光受影响，由计算知新楼在居民楼上的投影高约‎11米，‎ 故受影响 ‎ ‎（2）若要使超市采光不受影响，两楼至少相距：＝20×＝32（米） ‎