中考总复习数学测试题

中考总复习数学测试题

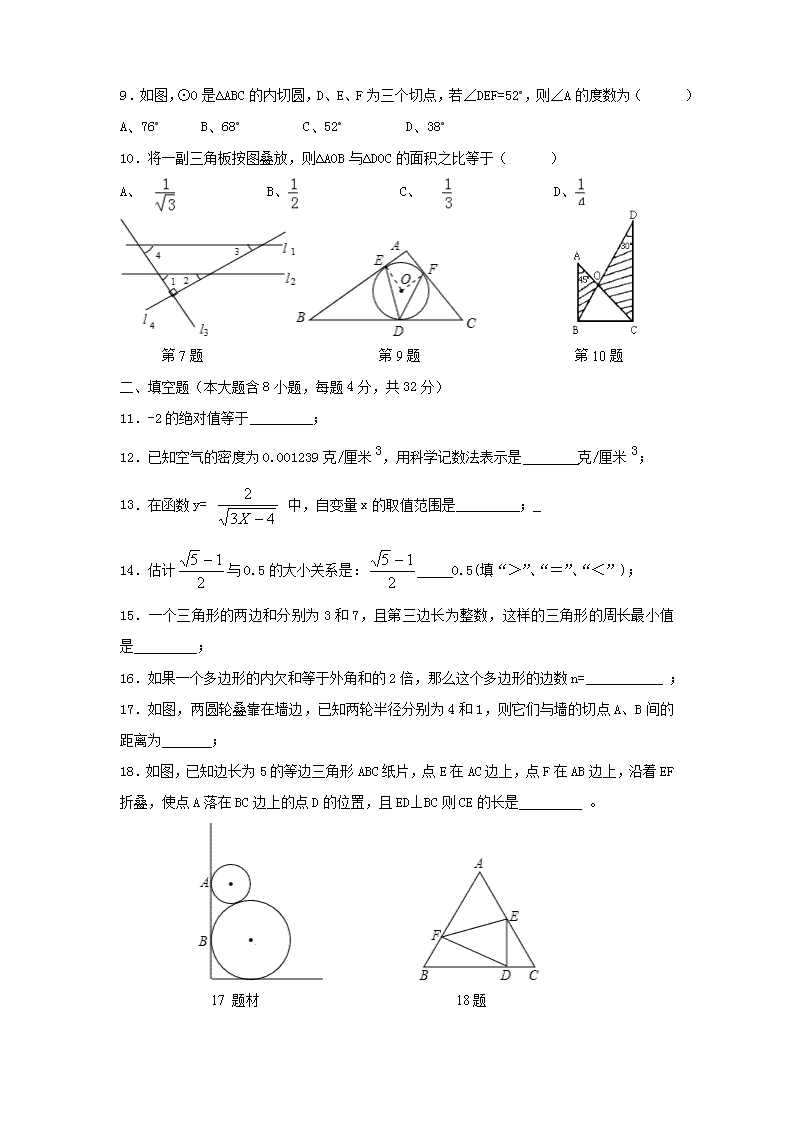
‎2012年初中毕业模拟测试 数学试卷 ‎（全卷总分150分。考试时间150分钟）‎ 一、选择题（本大题含10小题，每题3分，共30分）‎ ‎1．16的平方根是（ ）‎ A、4 B、±‎4 C、-4 D、±8‎ ‎2．若家用电冰箱冷藏室的温度是‎4℃‎，冷冻室比冷藏室的温度低22，则冷冻室的温度 为（ ）‎ A、‎-18℃‎ B、‎18℃‎ C、‎-26℃‎ D、‎‎26℃‎ ‎3．在下列四个图案中，既是轴对称图形，又是中心对称图形的是（ ）‎ A、 B、 ． C、 D、 ‎ ‎ ‎ ‎4．某校篮球队五名主力队员的身高分别是174、179、180、174、178（单位：cm），则这组数据的中位数是（ ）‎ A、 ‎174cm B、‎177cm C、‎178cm D、‎‎180cm ‎5．幼儿园的小朋友们打算选择一种形状、大小都相同的多边形朔料板铺活动室的地面，为了保证铺地时既无缝隙又不重叠，请你告诉他们下面形状的朔料板：①三角形；②四边形；③正五边形；④正六边形；⑤正八边形，可以选择的是（ ）‎ A、 ③④⑤ B、 ①②④ C、 ①④ D、①③④⑤‎ ‎6．已知圆锥的底面半径为3，高为4，则圆锥的侧面积为（ ）‎ A、10π B、 12π C、15π D、20π ‎7．如图，直线l1 ∥l2，l3⊥l4. 有三个命题，①∠1+∠3=90°；②∠2+∠3=90°；③∠2=∠4.下列说法中，正确的是（ ）‎ A、只有①正确 B、只有②正确 C、①和③正确 D、①②③都正确 ‎8．函数y=kx+b（k≠0）与y= y=（k≠0）在同一坐标中的图象可能是（ ）‎ A、 B、 C、 D、‎ ‎ ‎ ‎9．如图，⊙O是∆ABC的内切圆，D、E、F为三个切点，若∠DEF=52°，则∠A的度数为（ ）‎ A、76° B、68° C、52° D、38°‎ ‎10．将一副三角板按图叠放，则∆AOB与∆DOC的面积之比等于（ ）‎ A、 B、 C、 D、‎ 第7题 第9题 第10题 二、填空题（本大题含8小题，每题4分，共32分）‎ ‎11．-2的绝对值等于 ；‎ ‎12．已知空气的密度为‎0.001239克/厘米3，用科学记数法表示是 克/厘米3；‎ ‎13．在函数y= 中，自变量x的取值范围是 ； ‎ ‎14．估计与0.5的大小关系是： 0.5(填“＞”、“＝”、“＜”)； ‎ ‎15．一个三角形的两边和分别为3和7，且第三边长为整数，这样的三角形的周长最小值是 ；‎ ‎16．如果一个多边形的内欠和等于外角和的2倍，那么这个多边形的边数n= ；‎ ‎17．如图，两圆轮叠靠在墙边，已知两轮半径分别为4和1，则它们与墙的切点A、B间的距离为 ； ‎ ‎18．如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且ED⊥BC则CE的长是 。‎ ‎ ‎ ‎17 题材 18题 三、解答题（本大题含9小题，共88分，每题4分，）‎ ‎19．(本题6分)先化简，再求值：， 其中 ‎20．（本题8分）已知关于x的一元二次方程x2-（k+1）x-6=0的一个根是2，求方程的另一根和k的值。‎ ‎21．（本题8分）在两个布袋中分别装有三个小球，这三个球的颜色分别为红色、白色、绿色，其他滑区别。把两袋小球都搅匀后，再分别从两袋中各取出一个小球，试求取出两个相同颜色小球的概率（要求用树状图或列表方法求解）。‎ ‎22．（本题10分）如图，某公园入口处原有三阶台阶，每级台阶高为‎20cm，深为‎30cm。为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度。（tan12°≈0.2，精确到‎1cm）‎ ‎23．（本题10分）我区某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试,下表是这30名学生的测试成绩(分):‎ ‎4‎ ‎5‎ ‎7‎ ‎6‎ ‎3‎ ‎7‎ ‎9‎ ‎4‎ ‎5‎ ‎7‎ ‎7‎ ‎3‎ ‎7‎ ‎5‎ ‎6‎ ‎8‎ ‎7‎ ‎5‎ ‎6‎ ‎8‎ ‎6‎ ‎7‎ ‎4‎ ‎10‎ ‎5‎ ‎6‎ ‎7‎ ‎3‎ ‎9‎ ‎4‎ ‎(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;‎ ‎(2)求出这30名学生成绩的平均数、众数;‎ ‎（3）如果漫山遍野成绩6分以上（包括6分）为合格，请估计300名学生中成绩合格的约有多少人？‎ ‎24．（本题10分）直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形。方法如下：‎ 请你用上面图示的方法，解答下列问题：‎ ‎（1）对任意三角形，设计一种方案，将它分成若干块，再拼成一个与原三角形面积相等的矩形。‎ ‎（2）对任意四边形，设计一种方案，将它分成若干块，再拼成一个与原四边形面积相等的矩形。‎ ‎25．（本题10分）如图，在矩形ABCD中，AB=6，BC=8。将矩形ABCD沿CE折叠后，使点D恰好落在对角线AC上的点F处。‎ ‎（1）求EF的长 ‎（2）求梯形ABCE锝面积 ‎ ‎ ‎ ‎26．（本题12分）一条隧道的截面如图所示，它的上部是一个以AD为直径的半圆O，下部是一个矩形ABCD。‎ ‎（1）当AD=4米时，求隧道截面上部半圆O的面积； ‎ ‎（2）已知矩形ABCD相邻两边之和为8米，半圆O的半径为r米. ‎ ‎①求隧道截面的面积S（米2）关于半径r（米）的函数关系式（不要求写出r的取值范围）； ‎ ‎②若‎2米≤CD≤‎3米，利用函数图象求隧道截面的面积S的最大值（π取3.14，结果精确到‎0.1米） ‎ ‎ ‎ ‎27．（本题14分）如图1，已知抛物线的顶点为A（0，1），矩形CDEF的顶点C、F在抛物线上，D、E在x轴上，CF交y轴于点B（0，2），且其面积为8。‎ ‎⑴ 求此抛物线的解析式；‎ ‎⑵ 如图2，若P点为抛物线上不同于A的一点，连结PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R。‎ ‎①求证：PB=PS；‎ ‎②判断△SBR的形状；‎ ‎③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似，若存在，请找出M点的位置；若不存在，请说明理由。‎ ‎ ‎