2015河南唐河中考模拟1数学试题及答案

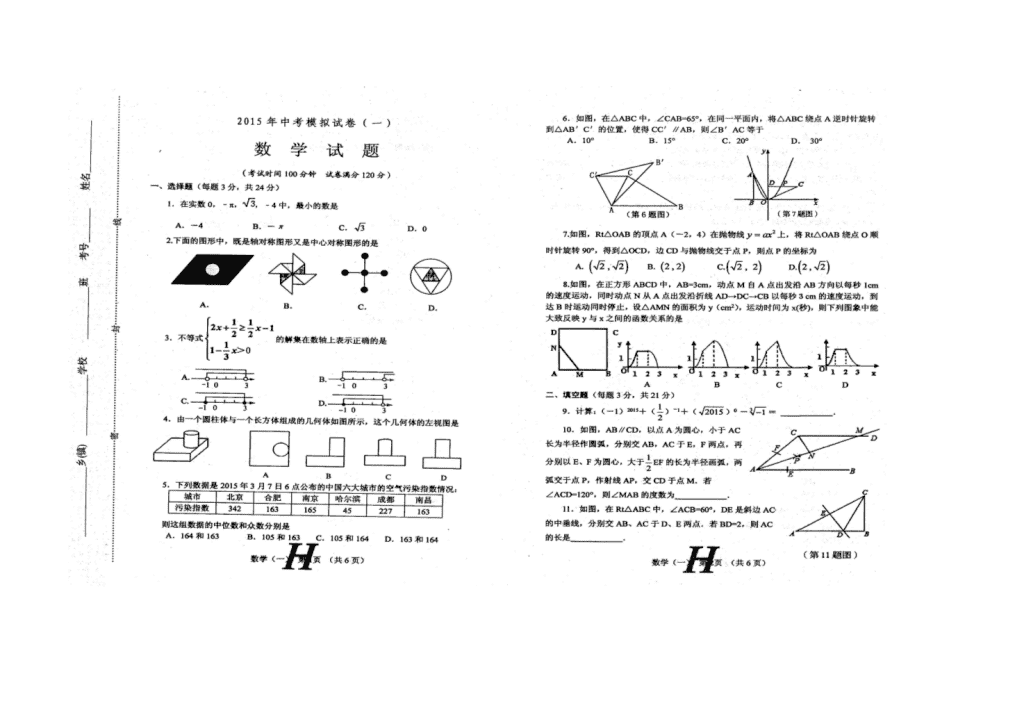
2015河南唐河中考模拟1数学试题及答案

数学（一）参考答案及评分标准 一、选择题（每题3分，共24分）‎ ‎1.A 2.C 3.D 4.D 5.A 6.B 7.C 8.B 二、填空题（每题3分，共21分）‎ ‎9. 3 10. 30(或30°) 11．4 12．8 13． 14. 15. 或5‎ 三、解答题（本大题共8个小题，满分75分）‎ ‎16.解：原式＝•……………………… 2分 ‎＝－，……………………… 4分 方程变形得：（x－1）（x－3）＝ 0，[或用配方法：（x－2）2 ＝1] …………5分 解得：x＝1或x＝3，……………………… 6分 当x＝1时，原式没有意义，舍去，（）…………………7分 当x＝3时，原式＝－．……………………… 8分 ‎17.解：（1）①△ODE≌△BOF；②△BOM≌△DON；③△ABD≌△CDB；④△AME≌△CFN；‎ ‎⑤△MBF≌△NDE；（写对2个得一分，写出4个得2分）……………… 2分[来#@源%:中&^教网]‎ 选法不唯一．但策略上能赢得时间．‎ 如选①△DOE≌△BOF；[来~#源%*:^中国教育出版网]‎ 证明：∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC．‎ ‎∴∠EDO=∠FBO，∠E=∠F．……………………… 4分[中国~教育出@*版&网%]‎ 又∵OD=OB，‎ ‎∴△DOE≌△BOF（AAS）．………………………5分[来源:中%^国#教育出~版网&]‎ 选②△BOM≌△DON．[来源:中%^国教育出~版网#&]‎ 证明：∵四边形ABCD是平行四边形，‎ ‎∴AB∥CD．‎ ‎∴∠MBO=∠NDO，∠BMO=∠DNO．‎ 又∵BO=DO，‎ ‎∴△BOM≌△DON（AAS）．[来源~%:zz#st*ep.co&m]‎ 选③△ABD≌△CDB．[来源&:中教网@*#^]‎ 证明：∵四边形ABCD是平行四边形，‎ ‎∴AD=CB，AB=CD．‎ 又∵BD=DB，‎ ‎∴△ABD≌△CDB（SSS）．[来源:中国教^育出&版@网~*]‎ ‎（2）绕点O旋转180°后得到或以点O为中心作对称变换得到．……………… 7分 ‎（因为平行四边形是中心对称图形，各对全等三角形中的一个都是以其中一个三角形绕点O旋转180°后得到或以点O为中心作对称变换得到．）[来@源*:中%&教#网]‎ ‎（3）问题有多种．如①求证：∠AME=∠CNF；②本题蕴含了哪些数学思想？等等．‎ ‎……………………… 9分[来#%源:中国教育&出版^网@]‎ 点评： 本题考了全等三角形和平行四边形的性质和中心对称图形，比较容易．（1）的开放性（不限制证明△ODE≌△BOF），增加题目的“含金量”．‎ ‎18. 解：（1）A组的频数是： 2；…………………… 2分 调查样本的容量是： 50 ；……………………… 4分 ‎（2）C组的频数是：50×40%=20，‎ Ｄ组的频数是:50×28%=41‎ E组的频数是:50×8%=4 ……………5分 如图．…………………7分[ww#w%.zzstep^.c*om~]‎ ‎(注:看图只被C组2分, 注明A、D、E频数1分)‎ ‎（3）∵1500×（28%+8%）=540，‎ ‎∴全社区月信息消费额不少于300元的户数是540户.…………………9分 ‎19.（1）∵AB∥CD ∴∠ABC+∠BCD=180°………………… 1分 ‎∵AB、BC、CD分别与⊙O相切于E、F、G，‎ ‎∴BO平分∠ABC，CO平分∠DCB，………………… 2分[来源%&:#中国教育出版~网*]‎ ‎∴∠OBC= ，∠OCB= ，………………… 3分[来源%:#zzstep.&c^om*]‎ ‎∴∠OBC+∠OCB=（∠ABC+∠DCB）= ×180°=90°，………4分 ‎∴∠BOC=90°，‎ ‎∴BO⊥CO．………………… 5分 ‎[中&国教育#*~出^版网]‎ ‎（2）解：连接OF，则OF⊥BC，‎ ‎∴Rt△BOF∽Rt△BCO，‎ ‎∴ = ，………………… 6分 ‎ ‎∵在Rt△BOF中，BO=6，CO=8，‎ ‎∴BC= =10，‎ ‎∴ = ，∴BF=3.6，…………………7分 ‎∵AB、BC、CD分别与⊙O相切，‎ ‎∴BE=BF=3.6，CG=CF，…………………8分 ‎∵CF=BC﹣BF=10﹣3.6=6.4．‎ ‎∴CG=CF=6.4．………………… 9分 ‎（1）证法二：连接OE、OF、 OG，‎ ‎∵AB、BC、CD分别与⊙O相切于E、F、G，‎ ‎∴OE⊥AB，OG⊥DC，OF⊥BC，且OE＝OG＝OF……………1分 ‎∵AB∥CD ∴EG是⊙O的直径………………… 2分 ‎∴Rt△BOE≌Rt△BOF，Rt△COG≌Rt△COF，‎ ‎∴∠EOB =∠FOB,∠GOC=∠FOC ………………… 3分 ‎∴∠EOB+∠GOC=（∠FOB+∠FOC）=∠BOC ，‎ ‎∴∠BOC = ×∠EOG = ×180°=90°，‎ ‎∴BO⊥CO．………………… 5分 ‎（2）解法二：在Rt△BOF中，BO=6，CO=8，[w#ww.zzs%~@tep^.com]‎ ‎∴BC= =10，………………… 6分 ‎∵OF⊥BC，∴OF ＝＝………………7分[来源:~中@国^教#育%出版网]‎ 在Rt△OEB中，BO=6，EO= ，‎ ‎∴EB= = (＝3.6) ………………… 8分 在Rt△OGC中，CO=8，GO= ，‎ ‎∴GC= = (=6.4) ………………… 9分 ‎20.解：如图所示，…………… 2分 AB代表小明所处位置到地面的距离，即米，‎ CD代表“中原第一高楼”的高，………………… 3分 作AE⊥CD于点E.[中国教育*出&@^#版网]‎ 由题意可知，四边形ABD E是矩形，所以米.‎ 在Rt△ADE中，∵，，‎ ‎∴，∴ .…………… 5分 在Rt△AEC中，∵，，‎ ‎∴，∴，…………… 7分 ‎∴（米），‎ ‎∴“中原第一高楼”高米. ……………9分 ‎21．解：（1）设每件甲种玩具的进价为x元，乙种为y元，…………1分 由题意得，……………………………………2分 解得，……………………………………3分 答：件甲种玩具的进价是30元，每件乙种玩具的进价是27元；………4分 ‎（2）当0＜x≤20时，y=30x；…………………5分 当x＞20时，y=20×30+（x﹣20）×30×0.7=21x+180；………………7分 ‎（3）当x＞20时，因为购进玩具x件甲种需要花费（21x+180）元，‎ 而购乙种玩具x件需要花费27x元；‎ 当27x=21x+180，则x=30‎ 所以当购进玩具正好30件，购甲种、乙种玩具费用一样，选购其中一种即可；[来源:中国教*#育^&出版%网]‎ ‎……………………………………8分 当x＞30， 27x＞21x+180‎ 即当购进玩具超过30件，选择购甲种玩具省钱；…………………9分 当x＜30，则27x＜21x+180‎ 即当购进玩具少于30件，选择购乙种玩具省钱．…………………10分[www.zz&^s#tep.c*om~]‎ 点评： 此题考查二元一次方程组，一次函数，一元一次不等式的运用，理解题意，正确劣势解决问题．‎ ‎22. 解:（2）AE=CD，AE⊥CD，‎ 证明：设CD分别交AE、AB于K、O，[ww*&w.zzste^#p.c@om]‎ ‎∵∠DBE=∠ABC=90°，‎ ‎∴∠DBE＋∠ABD=∠ABC＋∠ABD，即∠ABE=∠DBC，‎ 在△AEB和△CDB中，‎ ‎∴△AEB≌△CDB（SAS）………………………………2分 ‎∴AE＝CD，∠EAB＝∠DCB……………………………3分 ‎∵∠DCB+∠COB＝90°，∠AOK=∠COB ‎∴∠AOK+∠OAK=90°‎ ‎∴∠AKC=90°∴AE⊥CD．………………………………5分 ‎（3）AE= CD，（或CD=kAE）AE⊥CD，………………………………6分 证明：设CD分别交AE、AB于K、O，‎ 在△AEB和△CDB中，[来&源:中教^@*#网]‎ ‎∵BC=kAB，DB=kEB，‎ ‎∴ = = ，………………………………7分 ‎∵∠DBE=∠ABC=90°，[中国教@&育出*版网~#]‎ ‎∴∠DBE＋∠ABD=∠ABC＋∠ABD，‎ ‎∴∠ABE=∠DBC，[w@ww.zzs*&te#p.com~]‎ ‎∴△AEB∽△CDB，………………………………8分 ‎∴，∠EAB＝∠DCB ‎∴AE= CD，‎ ‎∵k＞1，∴AE≠CD，‎ ‎∵∠DCB+∠COB＝90°，∠AOK=∠COB[中^国教育&#*~出版网]‎ ‎∴∠AOK+∠OAK=90°‎ ‎∴∠AKC=90°∴AE⊥CD．………………………………10分 ‎23．（11分）解：（1）∵点（1, -5）和（-2, 4）在抛物线上 ‎………………………………………2分[中&国教#育^@出*版网]‎ 即…………………………………………………3分 ‎∴抛物线解析式为……………………………………………………4分 ‎（2）如图可知，∵‎ ‎∴N(m, m)，M(m, m2 - 2m - 4) P（m，0）…………………………………5分 由（1）知，‎ 令，得，‎ 即为抛物线与x轴两个交点的横坐标，‎ ‎∴当，点N在点M的上方 ‎∴MN = yN - yM ‎ = m-(m2 - ‎2m- 4)[来源^@:~中国教育出版*网&]‎ ‎ = - m2 + ‎3m + 4…………………7分 ‎（3）存在；‎ 由（２）得MN = - m2 + 3m + 4‎ 联立方程组解得 ‎∴A(-1, -1)，B(4, 4) ………………………………8分 作BC⊥MN于点C，则BC=4—m，OP=m，‎ S= MN•OP+ MN•BC=2（—m2+‎3m+4）‎ ‎………………………………10分 ‎∵—2＜0，‎ ‎∴当m= 时，S有最大值………………………………11分[中国教@育出版#~^网*]‎