中考数学试题分类汇编150套专题二十九尺规作图

中考数学试题分类汇编150套专题二十九尺规作图

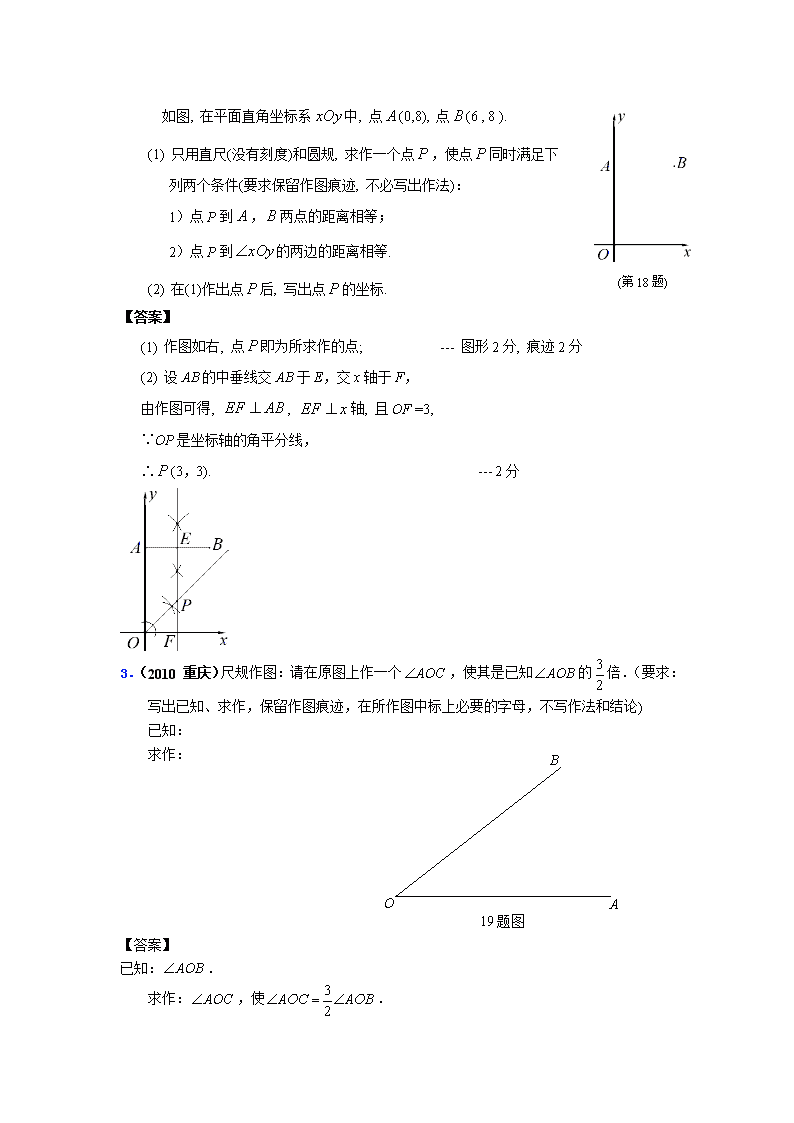
一、选择题 ‎1．（2010台湾） 如图(十二)，直线CP是的中垂线且交于P，其中 ‎ =2。甲、乙两人想在上取两点D、E，使得=‎ ‎ ==，其作法如下： (甲) 作ÐACP、ÐBCP之角平分线，分别交于D、E，‎ ‎ 则D、E即为所求 (乙) 作、之中垂线，分别交于D、E，则D、‎ ‎ E即为所求对于甲、乙两人的作法，下列判断何者正确？ (A) 两人都正确 (B) 两人都错误 (C) 甲正确，乙错误 (D) 甲错误，乙正确。‎ A B C P 图(十二)‎ ‎【答案】D ‎ ‎2．（2010浙江绍兴）如图,已知△ABC,分别以A,C为圆心,BC,AB长为半径画弧,两弧在直线BC上方交于点D,连结AD,CD.则有( )‎ 第8题图 B A C A.∠ADC与∠BAD相等 B.∠ADC与∠BAD互补 C.∠ADC与∠ABC互补 D.∠ADC与∠ABC互余 ‎【答案】B ‎ ‎3．（2010广东佛山）尺规作图是指 A．用直尺规范作图 B．用刻度尺和尺规作图 C．用没有刻度的直尺和圆规作图 D．直尺和圆规是作图工具 ‎【答案】C ‎ 二、填空题 ‎1．（2010四川凉山）已知：，求作的平分线；根据第16题图所示，填写作法：‎ ‎① 。‎ ‎② 。‎ ‎③ 。‎ ‎【答案】‎ ‎2．（2010江苏宿迁）数学活动课上，老师在黑板上画直线平行于射线AN(如图)，让同学们在直线l和射线AN上各找一点B和C，使得以A、B、C为顶点的三角形是等腰直角三角形．这样的三角形最多能画 ▲ 个．‎ ‎【答案】3‎ 三、解答题 ‎1．（2010山东青岛）如图，有一块三角形材料（△ABC），请你画出一个圆，使其与△ABC的各边都相切.‎ A B C ‎【答案】正确画出两条角平分线，确定圆心； 2分 确定半径； 3分 正确画出圆并写出结论． 4分 ‎2．（2010浙江杭州） (本小题满分6分) ‎ ‎.‎ ‎(第18题)‎ ‎ 如图, 在平面直角坐标系中, 点(0,8), 点(6 , 8 ).‎ ‎(1) 只用直尺(没有刻度)和圆规, 求作一个点，使点同时满足下 列两个条件(要求保留作图痕迹, 不必写出作法)： ‎ ‎1）点P到，两点的距离相等；‎ ‎2）点P到的两边的距离相等. ‎ ‎(2) 在(1)作出点后, 写出点的坐标.‎ ‎【答案】‎ ‎(1) 作图如右, 点即为所求作的点; --- 图形2分, 痕迹2分 ‎(2) 设AB的中垂线交AB于E，交x轴于F，‎ 由作图可得, , 轴, 且OF =3, ‎ ‎∵OP是坐标轴的角平分线，‎ ‎∴(3，3). --- 2分 ‎3．（2010 重庆）尺规作图：请在原图上作一个，使其是已知的倍．（要求：写出已知、求作，保留作图痕迹，在所作图中标上必要的字母，不写作法和结论)‎ 已知：‎ B O A ‎19题图 ‎ 求作：‎ ‎【答案】‎ 已知：．‎ 求作：，使．‎ ‎19题答图 作图如下：‎ ‎4．（2010重庆市潼南县）（6分）画一个等腰△ABC，使底边长BC=a，底边上的高为h（要求：用尺规作图，保留作图痕迹，写出已知，求作，不写作法和证明）.‎ 已知：‎ ‎ 求作：‎ ‎【答案】已知：线段a、h ‎ 求作：一个等腰△ABC使底边BC=a，底边BC上的高为h ‎ ‎----------------------------------------------1分 画图（保留作图痕迹图略）--------------------------6分 ‎5．（2010江苏泰州）已知△ABC，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法），并根据要求填空：‎ ‎(1)作∠ABC的平分线BD交AC于点D；‎ ‎(2)作线段BD的垂直平分线交AB于点E，交BC于点F．‎ 由⑴、⑵可得：线段EF与线段BD的关系为 ‎ ‎【答案】⑴、⑵题作图如下：由作图可知线段EF与线段BD的关系为：互相垂直平分．‎ ‎． ‎ ‎6．（2010重庆綦江县）尺规作图：如图，已知△ABC．‎ 求作△A1B1C1，使A1B1＝AB，∠B1＝∠B，B1C1＝BC．‎ ‎（作图要求：写已知、求作，不写作法，不证明，保留作图痕迹）‎ 已知：‎ 求作：‎ ‎ ‎ ‎【答案】‎ 已知：如图，△ABC．‎ 求作：△A1B1C1，使A1B1＝AB，∠B1＝∠B，B1C1＝BC．‎ ‎7．（2010 珠海）如图，在梯形ABCD中，AB∥CD ‎（1）用尺规作图方法，作∠DAB的角平分线AF（只保留作图痕迹，不写作法和证明）‎ ‎（2）若AF交CD边于点E，判断△ADE的形状（只写结果）‎ ‎【答案】解：(1)所以射线AF即为所求 ‎(2)△ADE是等腰三角形 ‎8．（2010 广西玉林、防城港）如图7，Rt△ABC中，∠C＝90，AC＝4，BC =３，‎ ‎（1）根据要求用尺规作图：作斜边AB边上的高CD，垂足为D；（不写作法，只保留作图痕迹。玉林市的考生再用水性笔将作图痕迹加黑）‎ ‎（2）求CD的长 ‎【答案】（1）略 ‎（2）AB＝5，根据相等有，ABCD＝ACBC 所以CD＝‎ ‎9．（2010 重庆江津）如图，有分别过A、B两个加油站的公路、相交于点O，现准备在∠AOB内建一个油库，要求油库的位置点P满足到A、B两个加油站的距离相等，而且P到两条公路、的距离也相等。请用尺规作图作出点P（不写作法，保留作图痕迹）．‎ ‎【答案】‎ ‎10．（2010青海西宁）如图，在△中，AD⊥BC,垂足为D. ‎ (1) 尺规作图（不写作法，保留作图痕迹）：作△的外接圆⊙O，作直径AE，连接BE.‎ (2) 若AB=8,AC=6,AD=5,求直径AE的长.(证明△∽△.)‎ ‎ ‎ ‎【答案】解：（1）正确作出△的外接圆⊙O（图略）‎ ‎ 正确作出直径AE（图略）‎ ‎ （2）证明：由作图可知AE为⊙O的直径 ‎ ∴∠ABE=90°（直径所对的圆周角是直角）‎ ‎ ∵AD⊥BC ‎ ∴∠ADC=90°‎ ‎ ∴∠ABE=∠ADC ‎ ∵=‎ ‎ ∴∠E=∠C ‎ ∴△ABE∽△ADC ‎ ‎11．（2010年山西）山西民间建筑的门窗图案中，隐含着丰富的数学艺术之美，图1是其中一个代表，该窗格图案是以图2为基本图案经过图形变换得到的，图3是图2放大后的一部分，虚线给出了作图提示，请用圆规和直尺画图。‎ ‎ （1）根据图2将图3将补充完整；‎ ‎ （2）在图4的正方形中，用圆弧和线段设计一个美观的轴对称或中心对称图形。‎ ‎【答案】．解：（1）略 ‎ （2）图略，答案不唯一，‎ ‎12．（2010湖北宜昌）如图，已知Rt△ABC和Rt△EBC，°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切，D为切点，AD//BC。‎ ‎（1）用尺规确定并标出圆心O；（不写做法和证明，保留作图痕迹）‎ ‎（2）求证：[来源:Zxxk.Com]‎ ‎（3）若AD=1，，求BC的长。（8分）‎ ‎【答案】（1）（提示：O即为AD中垂线与AC的交点或过D点作EC的垂线与AC的交点等）.‎ 能见作图痕迹，作图基本准确即可,漏标O可不扣分 2分 ‎（2）证明:连结OD．∵AD∥BC ， ∠B=90°，∴∠EAD=90°．‎ ‎∴∠E+∠EDA=90°，即∠E=90°－∠EDA．‎ 又圆O与EC相切于D点，∴OD⊥EC．‎ ‎∴∠EDA+∠ODA=90°，即∠ODA=90°－∠EDA．[来源:Z_xx_k.Com]‎ ‎∴∠E=∠ODA 3分 ‎（说明：任得出一个角相等都评1分）‎ 又OD=OA，∴∠DAC=∠ODA，∴∠DAC=∠E． 4分 ‎∵AD∥BC，∴∠DAC=∠ACB，∴∠E=∠ACB． 5分 ‎（3）Rt△DEA中，tan∠E=，又tan∠E=tan∠DAC= ，‎ ‎∵AD=1∴EA=． 6分