中考数学复习专项练习卷反比例函数含答案解析

中考数学复习专项练习卷反比例函数含答案解析

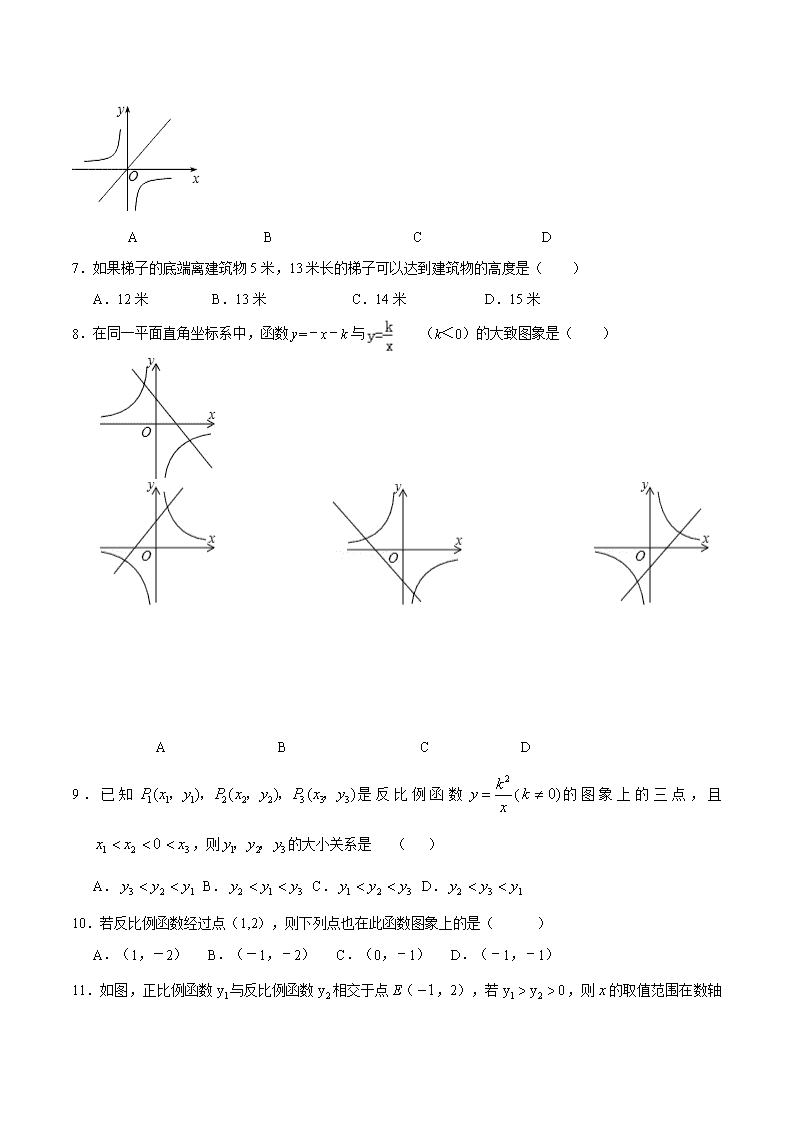
‎2013－2014学年度数学中考二轮复习专题卷 反比例函数 学校:___________姓名：___________班级：___________考号：___________‎ 一、选择题 ‎1．下列函数中，图象经过点（1，﹣1）的反比例函数关系式是 A． B． C． D．‎ ‎2．下列四个点中，在反比例函数的图象上的是【 】‎ A．（3，﹣2） B．（3，2） C．（2，3） D．（﹣2，﹣3）‎ ‎3．在函数y=中，自变量x的取值范围是（　　）‎ A． x＞0 B． x≠0 C． x＞1 D． x≠1‎ ‎4．已知反比例函数的图象经过点（1，2），则此函数图象所在的象限是（　　）‎ A．一、三 B．二、四 C．一、三 D． 三、四 ‎5．下列函数中，是反比例函数的是（　　）‎ A． y=5﹣x B． C．y=2013x D． ‎ ‎6．在同一平面直角坐标系中，正比例函数y=（m﹣1）x与反比例函数y=的图象的大体位置不可能是（　　）‎ ‎ ‎ ‎ A B C D ‎7．如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（　　）‎ A．12米 B．13米 C．14米 D．15米 ‎8．在同一平面直角坐标系中，函数y=﹣x﹣k与（k＜0）的大致图象是（　　）‎ ‎ ‎ ‎ A B C D ‎9．已知是反比例函数(的图象上的三点，且，则的大小关系是 （ ） ‎ A． B． C． D．‎ ‎10．若反比例函数经过点（1,2），则下列点也在此函数图象上的是（ ）‎ A．（1，－2） B．（－1，﹣2） C．（0，﹣1） D．（﹣1，﹣1）‎ ‎11．如图，正比例函数与反比例函数相交于点E（，2），若，则的取值范围在数轴上表示正确的是【 】‎ ‎ ‎ ‎ A B ‎ ‎ ‎ C D ‎ ‎ ‎12．函数y1=x和的图象如图所示，则y1＞y2的x取值范围是 A．x＜﹣1或x＞1 B．x＜﹣1或0＜x＜1‎ C．﹣1＜x＜0或x＞1 D．﹣1＜x＜0或0＜x＜1‎ ‎13．已知A（，），B（2，）两点在双曲线上，且，则m的取 值范围是【 】‎ A． B． 　 C． D．‎ ‎14．当时，函数的图象在【 】‎ A．第四象限 B．第三象限 C．第二象限 D．第一象限 ‎ ‎15．若反比例函数的图象经过点（5，﹣1）．则实数k的值是 A． B． C． D．5‎ ‎16．如图，P1是反比例函数在第一象限图像上的一点，点A1 的坐标为(2，0)．若△P1O A1与△P2 A1 A2均为等边三角形，则A2点的横坐标为 A． B． C． D．‎ ‎ ‎ ‎17．如图，直线与双曲线y=交于A，B两点，则当线段AB的长度取最小值时，a的值为 A．0 B．1 C．2 D．5‎ ‎18．如图，等边△OAB的边OB在x轴的负半轴上，双曲线过OA的中点，已知等边三角形的边长是4，则该双曲线的表达式为 A． B． C． D．‎ ‎ ‎ ‎19．如图，在平面直角坐标系中，∠AOB=90°，∠OAB=30°，反比例函数的图象经过点A，反比例函数的图象经过点B，则下列关于m，n的关系正确的是 A. m=﹣3n B. C. D. ‎ ‎20．如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A。C分别在x轴、y轴上，反比例函数的图象与正方形的两边AB、BC分别交于点M、N，ND⊥x轴，垂足为D，连接OM、ON、MN。‎ 下列结论：①△OCN≌△OAM；②ON=MN； ③四边形DAMN与△MON面积相等；④ 若∠MON=450，MN=2，则点C的坐标为。其中正确的个数是【 】‎ A．1 　B．2　　 C．3　 　D．4‎ ‎ ‎ ‎21．如图，反比例函数（x＞0）的图象经过矩形OABC对角线的交点M，分别于AB、BC交于点D、E，若四边形ODBE的面积为9，则k的值为【 】‎ A．1 B．2 C．3 D．4‎ ‎22．如图，点B在反比例函数（x＞0）的图象上，横坐标为1，过点B分别向x轴，y轴作垂线，垂足分别为A，C，则矩形OABC的面积为 A．1 B．2 C． 3 D． 4‎ ‎ ‎x y C O A B 二、填空题 ‎23．反比例函数的图象经过点（2，﹣1），则k的值为　 　．‎ ‎24．若反比例函数的图象经过点（2，4），则k的值为　 　．‎ ‎25．如图,点A是反比例函数图象上的一点,过点A分别向x轴、y轴作垂线, 若矩形ABOC的面积为3,则这个反比例函数的关系式是 .‎ ‎26．已知正比例函数与反比例函数的图象的一个交点坐标为（－1，2‎ ‎），则另一个交点的坐标为 ．‎ ‎27．已知一个函数的图象与的图象关于y轴成轴对称，则该函数的解析式为　 　．‎ ‎28．如图，直线AB交双曲线于Ａ、B，交x轴于点C,B为线段AC的中点，过点B作BM⊥x轴于M，连结OA.若OM=2MC,S⊿OAC=12，则k的值为 .‎ ‎ ‎ ‎29．李老师开车从甲地到相距240千米的乙地，如果邮箱剩余油量 y（升）与行驶里程x（千米）之间是一次函数关系，其图像如图所示，那么到达乙地时邮箱剩余油量是 ______________升．‎ ‎30．若反比例函数的图象经过点A（1，2），则k= ．‎ ‎31．设有反比例函数，（x1，y1），（x2，y2）为其图象上两点，若x1＜0＜x2，y1＞y2，则k的取值范围　 　．‎ ‎32．如图，两个反比例函数和在第一象限内的图象分别是C1和C2，设点P在C1上，PA⊥x轴于点A，交C2于点B，则△POB的面积为　 　．‎ ‎ ‎ ‎33．如图，已知A点是反比例函数（k≠0）的图象上一点，AB⊥y轴于B，且△ABO的面积为3，则k的值为　 　．‎ ‎34．如图，已知直线与双曲线（k＞0）交于A、B两点，点B的坐标为，C为双曲线（k＞0）上一点，且在第一象限内，若△AOC的面积为6，则点C的坐标为　 　．‎ ‎ ‎ ‎35．（2013年四川自贡4分）如图，在函数的图象上有点P1、P2、P3…、Pn、Pn+1，点P1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P1、P2、P3…、Pn、Pn+1分别作x轴、y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S1、S2、S3…、Sn，则S1=　 　，Sn=　 　．（用含n的代数式表示）‎ ‎36．如图，等腰直角三角形ABC顶点A在x轴上，∠BCA=90°，AC=BC=2，反比例函数（x＞0）的图象分别与AB，BC交于点D，E．连结DE，当△BDE∽△BCA时，点E的坐标为　 　．‎ ‎ ‎ ‎37．如图，点P是反比例函数图象上的点，PA垂直x轴于点A（－1，0），点C的坐标为（1，0），PC交y轴于点B，连结AB，已知AB=。（1）k的值是　 　；‎ ‎（2）若M（a，b）是该反比例函数图象上的点，且满足∠MBA＜∠ABC，则a的取值范围是　 　。‎ 三、计算题 ‎38．已知一次函数的图象与反比例函数图象交于点 P（4，n）。‎ 求P点坐标.‎ ‎39．如图，矩形的对角线经过坐标原点，矩形的边分别平行于坐标轴，点在反比例函数的图象上.若点的坐标为，求的值.‎x y O A B C D ‎40．如图，是反比例函数的图象的一支．根据给出的图象回答下列问题：‎ ‎（1）该函数的图象位于哪几个象限？请确定m的取值范围；‎ ‎（2）在这个函数图象的某一支上取点A（x1，y1）、B（x2，y2）．如果y1＜y2，那么x1与x2有怎样的大小关系？‎ 四、解答题 ‎41．如图，在平面直角坐标系中，反比例函数y=（x＞0）的图象和矩形ABCD在第一象限，AD平行于x轴，且AB=2，AD=4，点A的坐标为（2，6）．‎ ‎（1）直接写出B、C、D三点的坐标；‎ ‎（2）若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并 求矩形的平移距离和反比例函数的解析． ‎ ‎42．已知，在平面直角坐标系xOy中，点A在x轴负半轴上，点B在y轴正半轴上，OA=OB，函数的图象与线段AB交于M点，且AM=BM．‎ ‎（1）求点M的坐标；（2）求直线AB的解析式．‎ ‎43．已知正比例函数y=ax与反比例函数的图象有一个公共点A（1，2）．‎ ‎（1）求这两个函数的表达式；‎ ‎（2）画出草图，根据图象写出正比例函数值大于反比例函数值时x的取值范围．‎ ‎44．如图，科技小组准备用材料围建一个面积为60ｍ2的矩形科技园ABCD，其中一边AB靠墙，墙长为12ｍ。设AD的长为ｘｍ，DC的长为ｙｍ。‎ ‎（1）求ｙ与ｘ之间的函数关系式；‎ ‎（2）若围成矩形科技园ABCD的三边材料总长不超过26ｍ，材料AD和DC的长都是整米数，求出满足条件的所有围建方案。‎ ‎45．如图，已知直线与反比例函数的图象交于A、B两点，与x 轴、y轴分别相交于C、D两点。‎ ‎（1）如果点A的横坐标为1，利用函数图象求关于x的不等式的解集；‎ ‎（2）是否存在以AB为直径的圆经过点P（1，0）？若存在，求出m的值；若不存在，请说明理由。‎ ‎46．如图，点A（1，a）在反比例函数（x＞0）的图象上，AB垂直于x轴，垂足为点B，将△ABO沿x轴向右平移2个单位长度，得到Rt△DEF，点D落在反比例函数（x＞0）的图象上．（1）求点A的坐标；（2）求k值．‎ ‎47．某服装店以每件40元的价格购进一批衬衫，在试销过程中发现：每月销售量y（件）与销售单价x（x为正整数）（元）之间符合一次函数关系，当销售单价为55元时，月销售量为140件；当销售单价为70元时，月销售量为80件．‎ ‎（1）求y与x的函数关系式；‎ ‎（2）如果每销售一件衬衫需支出各种费用1元，设服装店每月销售该种衬衫获利为w元，求w与x之间的函数关系式，并求出销售单价定为多少元时，商场获利最大，最大利润是多少元？‎ ‎48．如图，在平面直角坐标系xOy中，一次函数y=ax+b的图象与反比例函数的图象相交于点A（m，1）、B（﹣1，n），与x轴相交于点C（2，0），且AC=OC．‎ ‎（1）求该反比例函数和一次函数的解析式；（2）直接写出不等式ax+b≥的解集．‎ ‎49．（2013年浙江义乌12分）如图1，已知（x＞）图象上一点P，PA⊥x轴于点A（a，0），点B坐标为（0，b）（b＞0），动点M是y轴正半轴上B点上方的点，动点N在射线AP上，过点B作AB的垂线，交射线AP于点D，交直线MN于点Q，连结AQ，取AQ的中点为C．‎ ‎（1）如图2，连结BP，求△PAB的面积；‎ ‎（2）当点Q在线段BD上时，若四边形BQNC是菱形，面积为，求此时P点的坐标；‎ ‎（3）当点Q在射线BD上时，且a=3，b=1，若以点B，C，N，Q为顶点的四边形是平行四边形，求这个平行四边形的周长．‎ ‎50．如图①，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，sin∠AOB=，反比例函数y=（k＞0）在第一象限内的图象经过点A，与BC交于点F．‎ ‎（1）若OA=10，求反比例函数解析式；‎ ‎（2）若点F为BC的中点，且△AOF的面积S=12，求OA的长和点C的坐标；‎ ‎（3）在（2）中的条件下，过点F作EF∥OB，交OA于点E（如图②），点P为直线EF上的一个动点，连接PA，PO．是否存在这样的点P，使以P、O、A为顶点的三角形是直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．‎ 参考答案 ‎1．A ‎【解析】‎ 试题分析：根据点在曲线上点的坐标满足方程的关系，将（1，﹣1）代入各函数关系式验算，易得，（1，﹣1）满足。故选A。‎ ‎2．A。‎ ‎【解析】根据点在曲线上点的坐标满足方程的关系，将各点坐标代入验算，满足的点即为所求，易得，点（3，﹣2）满足。故选A。‎ ‎3．B ‎【解析】‎ 试题分析：根据分母不等于0列式计算即可得解．‎ 解：根据题意得，x≠0．‎ 故选B．‎ 点评：本题考查了函数自变量的范围，一般从三个方面考虑：‎ ‎（1）当函数表达式是整式时，自变量可取全体实数；‎ ‎（2）当函数表达式是分式时，考虑分式的分母不能为0；‎ ‎（3）当函数表达式是二次根式时，被开方数非负．‎ ‎4．A ‎【解析】‎ 试题分析：根据反比例函数图象的性质先求出k的取值范围，再确定图象所在的象限．‎ 解：由反比例函数y=的图象经过点（1，2），‎ 可得k=2＞0，则它的图象在一、三象限．‎ 故选A．‎ 点评：此题主要考查反比例函数y=的图象性质：（1）k＞0时，图象是位于一、三象限．（2）k＜0时，图象是位于二、四象限．‎ ‎5．D ‎【解析】‎ 试题分析：根据反比例函数的定义进行判断．‎ 解：A、y=5﹣x是一次函数．故本选项错误；‎ B、y=是正比例函数．故本选项错误；‎ C、y=2013x是正比例函数．故本选项错误；‎ D、y=﹣符合反比例函数的定义．故本选项正确；‎ 故选D．‎ 点评： 本题考查了反比例函数的定义，反比例函数解析式的一般形式（k≠0），也可转化为y=kx﹣1（k≠0）的形式．‎ ‎6．D ‎【解析】‎ 试题分析：根据题意，依次分析选项中的图象，根据图象，求出其参数的范围，并解看有无公共解，若有，则可能是它们的图象，若无解，则不可能是它们的图象；即可得答案．‎ 解：依次分析选项可得：‎ A、4m＞0，m﹣1＞0；解可得m＞1；故可能是它们的图象．‎ B、4m＞0，m﹣1＜0；解可得0＜m＜1；故可能是它们的图象．‎ C、4m＜0，m﹣1＜0；解可得m＜1；故可能是它们的图象．‎ D、4m＜0，m﹣1＞0；无解；故不可能是它们的图象．‎ 故选D．‎ 点评：本题考查正比例函数与反比例函数的图象性质，注意①正比例函数与反比例函数的图象与k的关系，②两个函数中参数的关系．‎ ‎7．A ‎【解析】‎ 试题分析：根据梯子、地面、墙正好构成直角三角形，再根据勾股定理解答即可．‎ 解：如图所示，AB=13米，BC=5米，根据勾股定理AC===12米．‎ 故选A．‎ 点评：此题是勾股定理在实际生活中的运用，比较简单．‎ ‎8．A ‎【解析】‎ 试题分析：根据k的符号及一次函数与反比例函数图象的性质解答．‎ 解：当k＜0时，﹣k＞0，反比例函数y=的图象在二，四象限，一次函数y=﹣x﹣k的图象过一、二、四象限，选项A符合；‎ 故选A．‎ 点评：本题主要考查了反比例函数和一次函数的图象性质，正确掌握它们的性质才能灵活解题．‎ ‎9．B ‎【解析】‎ 试题分析：∵，‎ ‎∴函数图象在第一、三象限，在每个象限内，y随x的增大而减小，‎ 又∵x1＜x2＜0＜x3，‎ ‎∴y2＜y1＜y3．‎ 故选B.‎ 考点：反比例函数的性质．‎ ‎10．B ‎【解析】‎ 试题分析：设反比例函数图象的解析式为，‎ ‎∵反比例函数的图象经过点（1，2），‎ ‎∴k=1×2=2，‎ 而1×（－2）=－2，－1×（－2）=2，0×（－1）＝0，－1×（－1）＝1.‎ ‎∴点（－1，－2）在反比例函数图象上．‎ 故选B．‎ 考点：反比例函数图像上点的坐标的特征．‎ ‎11．A。‎ ‎【解析】∵正比例函数y1与反比例函数y2相交于点E（﹣1，2），‎ ‎∴根据图象可知当y1＞y2＞0时x的取值范围是x＜﹣1。‎ ‎∴在数轴上表示为：。‎ 故选A。‎ ‎12．C。‎ ‎【解析】∵y1＞y2即函数y1=x的图象在的图象上方时，x的取值范围，‎ ‎∴根据图象，当﹣1＜x＜0或x＞1时，函数y1=x的图象在的图象上方。‎ 故选C。‎ ‎13．D。‎ ‎【解析】∵A（，），B（2，）两点在双曲线上，‎ ‎∴根据点在曲线上，点的坐标满足方程的关系，得。‎ ‎∵，∴，解得。故选D。‎ ‎14．A。‎ ‎【解析】根据反比例函数的性质：当时，图象分别位于第一、三象限；当时，图象分别位于第二、四象限。‎ ‎∵反比例函数的系数，∴图象两个分支分别位于第二、四象限。‎ ‎∴当时，图象位于第四象限。故选A。‎ ‎15．A ‎【解析】‎ 试题分析：根据点在曲线上点的坐标满足方程的关系，将（5，﹣1）代入得。故选A。‎ ‎16．C ‎【解析】‎ 试题分析：过点P1作P1C⊥OA2，垂足为C，‎ ‎∵△P1OA1为边长是2的等边三角形，OC=1，，‎ ‎∴P1（1，）。‎ 将P1（1，）代入，得k=。‎ ‎∴反比例函数的解析式为。‎ 过点P2作P2D⊥A1A2，垂足为D，‎ 设A1D=a，则，∴。‎ ‎∵在反比例函数的图象上，‎ ‎∴将代入，得。解得：。‎ ‎∵a＞0，∴。∴。∴。‎ ‎∴点A2的横坐标为。故选C。‎ ‎17．C ‎【解析】‎ 试题分析：反比例函数图象既是轴对称图形又是中心对称图形，只有当A、B、O三点共线时，才会有线段AB的长度最小，此时，。故选C。‎ ‎18．B ‎【解析】‎ 试题分析：如图，过点C作CD⊥OB于点D．‎ ‎∵△OAB是等边三角形，该等边三角形的边长是4，‎ ‎∴OA=4，∠COD=60°。‎ 又∵点C是边OA的中点，∴OC=2。‎ ‎∴OD=OC•cos60°=2×=1，CD=OC•sin60°=2×=。‎ ‎∴C（﹣1，）。‎ ‎∵双曲线过OA的中点C，∴，解得，k=﹣。‎ ‎∴该双曲线的表达式为．‎ 故选B。　‎ ‎19．A ‎【解析】‎ 试题分析：如图，过点B作BE⊥x轴于点E，过点A作AF⊥x轴于点F，‎ 设点A的坐标为（a，），点B坐标为（b，），‎ 则OE=﹣b，BE=，OF= a，AF=，‎ ‎∵∠OAB=30°，∴OA=OB。‎ ‎∵∠BOE+∠OBE=90°，∠AOF+∠BOE=90°，∴∠OBE=∠AOF。‎ 又∵∠BEO=∠OFA=90°，∴△BOE∽△OAF。‎ ‎∴，即，∴。‎ ‎∴m=﹣3n。故选A。‎ ‎20．C。‎ ‎【解析】设正方形OABC的边长为a，‎ 则A（a，0），B（a，a），C（0，a），M（a，），N（，a）。‎ ‎∵CN=AM= ，OC=OA= a，∠OCN=∠OAM=900，‎ ‎∴△OCN≌△OAM（SAS）。结论①正确。‎ 根据勾股定理，，，‎ ‎∴ON和MN不一定相等。结论②错误。‎ ‎∵，‎ ‎∴。结论③正确。‎ 如图，过点O作OH⊥MN于点H，则 ‎∵△OCN≌△OAM ，∴ON=OM，∠CON=∠AOM。‎ ‎∵∠MON=450，MN=2，‎ ‎∴NH=HM=1，∠CON=∠NOH=∠HOM=∠AOM=22.50。‎ ‎∴△OCN≌△OHN（ASA）。∴CN=HN=1。‎ ‎∴。‎ 由得，。‎ 解得：（舍去负值）。‎ ‎∴点C的坐标为。结论④正确。‎ ‎∴结论正确的为①③④3个。故选C。‎ ‎21．C。‎ ‎【解析】由题意得：E、M、D位于反比例函数图象上，‎ 则，‎ 过点M作MG⊥y轴于点G，作MN⊥x轴于点N，则S□ONMG=|k|。‎ 又∵M为矩形ABCO对角线的交点，‎ ‎∴S矩形ABCO=4S□ONMG=4|k|，‎ ‎∵函数图象在第一象限，k＞0，∴。‎ 解得：k=3。故选C。‎ ‎22．B ‎【解析】‎ 试题分析：∵点B在反比例函数（x＞0）的图象上，过点B分别向x轴，y轴作垂线，垂足分别为A，C，‎ ‎∴故矩形OABC的面积S=|k|=2。故选B。‎ ‎23．﹣2。‎ ‎【解析】根据点在曲线上点的坐标满足方程的关系，将点（2，﹣1）代入解析式可得k=2×（﹣1）=﹣2。‎ ‎24．8‎ ‎【解析】‎ 试题分析：根据点在曲线图上点的坐标满足方程的关系，把（2，4）代入，得，即。‎ ‎25．‎ ‎【解析】‎ 试题分析：设反比例函数的解析式为（k≠0），‎ 因为矩形ABOC的面积为3，所以|k|=3，‎ 所以k=±3，‎ 由图象在第二象限，‎ 所以k＜0，;k=－3,所以这个反比例函数解析式为．‎ 考点：反比例函数系数k的几何意义．‎ ‎26．（1，－2）‎ ‎【解析】‎ 试题分析：根据正比例函数与反比例函数的交点关于原点对称进行解答即可：‎ ‎∵正比例函数与反比例函数的图象均关于原点对称，∴两函数的交点关于原点对称。‎ ‎∵一个交点的坐标是（－1，2），∴另一个交点的坐标是（1，－2）。‎ ‎27．。‎ ‎【解析】设所求函数的解析式为，点（）在图象上，‎ ‎∵根据题意，（）关于y轴成轴对称的点（）在的图象上，‎ ‎∴。‎ ‎∴所求函数的解析式为。‎ ‎28．8‎ ‎【解析】‎ 试题分析：如图，过A作AN⊥OC于N，‎ ‎∵BM⊥OC，∴AN∥BM。‎ ‎ ∵点B为AC中点，∴MN=M，。‎ ‎∵OM=2MC，∴ON=MN=CM。‎ ‎∵点A在双曲线上，∴设A的坐标是（a，）（a＞0）。‎ ‎∴OC=3a，AN=。‎ ‎∵S△OAC=12，∴。‎ ‎29．20‎ ‎【解析】‎ 试题分析：设函数关系式为：，‎ ‎∵（0，35），（160，25）在函数图象上，‎ ‎∴。‎ ‎∴函数关系式为：。‎ ‎∴当时，，即到达乙地时邮箱剩余油量是20升。‎ ‎30．2。‎ ‎【解析】根据点在曲线上，点的坐标满足方程的关系，将A（1，2）代入，得。‎ ‎31．k＜2‎ ‎【解析】‎ 试题分析：∵（x1，y1），（x2，y2）为函数图象上两点，且当x1＜0＜x2时，y1＞y2，‎ ‎∴该反比例函数的图象位于第二、四象限。‎ ‎∴k﹣2＜0，解得，k＜2。‎ ‎32．1。‎ ‎【解析】∵PA⊥x轴于点A，交C2于点B，∴S△POA=×4=2，S△BOA=×2=1，‎ ‎∴S△POB=S△POA﹣S△BOA =2﹣1=1。‎ ‎33．6。‎ ‎【解析】因为过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值，即S=|k|，从而由△ABO的面积为3，得S△ABO=|k|=3。‎ ‎∵反比例函数的图象位于第一象限，k＞0，∴k=6。‎ ‎34．（2，4）‎ ‎【解析】‎ 试题分析：∵点B（﹣4，﹣2）在双曲线上，∴，解得∴k=8。‎ 根据中心对称性，点A、B关于原点对称，∴A（4，2）。‎ 如图，过点A作AE⊥x轴于E，过点C作CF⊥x轴于F，‎ 设点C的坐标为（a，），‎ 则 ‎。‎ ‎∵△AOC的面积为6，∴=6，整理得，a2+6a﹣16=0，解得a1=2，a2=﹣8（舍去）。‎ ‎∴==4。∴点C的坐标为（2，4）。‎ ‎35．4；。‎ ‎【解析】当x=2时，P1的纵坐标为4，‎ 当x=4时，P2的纵坐标为2‎ 当x=6时，P3的纵坐标为，‎ 当x=8时，P4的纵坐标为1，‎ 当x=10时，P5的纵坐标为：，‎ ‎…‎ ‎∴；‎ ‎；‎ ‎；‎ ‎…‎ ‎。‎ 考点：探索规律题（图形的变化类），反比例函数系数k的几何意义，曲线上点的坐标与方程的关系。‎ ‎36．。‎ ‎【解析】如图，∵∠BCA=90°，AC=BC=2，反比例函数（x＞0）的图象分别与AB，BC交于点D，E，‎ ‎∴∠BAC=∠ABC=45°，且可设E（a，），D（b，）。‎ ‎∴C（a，0），B（a，2），A（a－，0），‎ 设直线AB的解析式为，‎ ‎∴，解得。∴线AB的解析式为。‎ 又∵△BDE∽△BCA，∴∠BDE=∠BCA=90°。∴直线AB与直线DE垂直。‎ 如图，过点D作x轴的垂线，过点R作y轴的垂线，两线交于点H ，‎ 则△DEH为等腰直角三角形，∴HE=HD，即。∴。‎ 又∵点D在直线AB上，∴，即。‎ ‎∴，解得（舍去）。‎ ‎∴点E的坐标是。‎ ‎37．（1）；（2）0＜a＜2或。‎ ‎【解析】（1）依题意，AO=1，OC=1，∴AB是Rt△PAC斜边上的中线。‎ ‎∵AB=，∴PC=。‎ ‎∴在Rt△PAC中，AC=2，AP=，PC=， ‎ ‎∴根据勾股定理，得：，解得。‎ ‎∵，∴。‎ ‎（2）分两种情况：‎ ‎ ①当点M在x轴下方时，考虑∠MBA＝∠ABC的情况：当∠MBA＝∠ABC时，点M是PC与双曲线的另一个交点，由B（0,2）,C（1,0）易得直线PC的解析式为，与联立：‎ ‎，解得：或（点P坐标，舍去），‎ ‎∴当∠MBA＝∠ABC时，点M的坐标为（2，－2）。‎ ‎∴当∠MBA＜∠ABC时，0＜a＜2。‎ ②当点M在x轴上方时，考虑∠MBA＝∠ABC的情况：如图，将△ABC顺时针旋转至 ‎△EBA，延长BE交于点，则之间横坐标的值即为所求。过点E分别作ｘ轴和ｙ 轴的垂线，垂足分别为点F，G，设点E的坐标为（ｘ，ｙ），‎ 由旋转的性质，得AE=AC=2，BE=BA=。‎ 在Rt△AEF中，由勾股定理，得，即①，‎ 在Rt△BEG中，由勾股定理，得，即②，‎ ①－②，得，即③，‎ 将③代入②，得，解得或（舍去），‎ 将代入③得。‎ ‎∴点E的坐标为。‎ 设直线BE的解析式为，则。‎ ‎∴直线BE的解析式为。‎ 联立。‎ ‎∴。‎ 综上所述，a的取值范围是0＜a＜2或。‎ ‎38．P（4,2）‎ ‎【解析】‎ 试题分析：点 P（4，n）在反比例函数上，则n=2.‎ 考点：反比例函数 点评：本题难度较低，主要考查学生对反比例函数k值性质的掌握。‎ ‎39．‎ ‎ 【解析】‎ 考点：反比例函数综合题．‎ 分析：由点A的坐标为（－2，－2），矩形ABCD的边分别平行于坐标轴，可设D点坐标为（a，－2），B点坐标为（－2，b），则C点坐标为（a，b），又矩形ABCD的对角线BD经过坐标原点O，则直线BD的解析式可设为y=mx，然后把点D（a，－2），B点（－2，b）分别代入y=mx得到am=－2，－2m=b，易得ab=－ •（－2m）=4，再利用点C（a，b）在反比例函数的图象上，根据反比例函数图象上点的坐标特点得到2k+1=ab=4，解方程即可得到k的值．‎ 解：∵点A的坐标为（－2，－2），矩形ABCD的边分别平行于坐标轴，‎ ‎∴B点的横坐标为－2，D点的纵坐标为－2，‎ 设D点坐标为（a，－2），B点坐标为（－2，b），则C点坐标为（a，b），‎ ‎∵矩形ABCD的对角线BD经过坐标原点O，‎ ‎∴直线BD的解析式可设为y=mx，‎ 把点D（a，－2），B点（－2，b）分别代入y=mx得，am=－2，－2m=b，‎ ‎∴a=－，‎ ‎∴ab=－•（－2m）=4，‎ ‎∵点C（a，b）在反比例函数的图象上，‎ ‎∴2k+1=ab=4，‎ ‎∴k=．‎ 故答案为．‎ ‎40．（1）函数图象位于第二、四象限，m＜5。‎ ‎（2）①当y1＜y2＜0时，x1＜x2；‎ ‎②当0＜y1＜y2，x1＜x2。‎ ‎【解析】‎ 试题分析：（1）根据反比例函数图象的对称性可知，该函数图象位于第二、四象限，则m﹣5＜0，据此可以求得m的取值范围；‎ ‎（2）根据函数图象中“y值随x的增大而增大”进行判断。　‎ 解：（1）∵反比例函数图象关于原点对称，图中反比例函数图象位于第四象限，‎ ‎∴函数图象位于第二、四象限，则m﹣5＜0，解得，m＜5。‎ ‎∴m的取值范围是m＜5。‎ ‎（2）由（1）知，函数图象位于第二、四象限，‎ ‎∴在每一个象限内，函数值y随自变量x增大而增大。‎ ‎①当y1＜y2＜0时，x1＜x2；‎ ‎②当0＜y1＜y2，x1＜x2。‎ ‎41．(1) B（2，4），C（6，4），D（6，6）；(2) A、C落在反比例函数的图象上，平移距离为3，反比例函数的解析式是.‎ ‎【解析】‎ 试题分析：（1）根据矩形性质得出AB=CD=2，AD=BC=4，即可得出答案； （2）设矩形平移后A的坐标是（2，6－x），C的坐标是（6，4－x），得出k=2（6－x）=6（4－x），求出x，即可得出矩形平移后A的坐标，代入反比例函数的解析式求出即可．‎ 试题解析：（1）∵四边形ABCD是矩形，平行于x轴，且AB=2，AD=4，点A的坐标为（2，6）．‎ ‎∴AB=CD=2，AD=BC=4，‎ ‎∴B（2，4），C（6，4），D（6，6）；‎ ‎（2）A、C落在反比例函数的图象上，‎ 设矩形平移后A的坐标是（2，6－x），C的坐标是（6，4－x），‎ ‎∵A、C落在反比例函数的图象上，‎ ‎∴k=2（6－x）=6（4－x），‎ x=3，‎ 即矩形平移后A的坐标是（2，3），‎ 代入反比例函数的解析式得：k=2×3=6，‎ 即A、C落在反比例函数的图象上，矩形的平移距离是3，反比例函数的解析式是.‎ 考点：1．矩形性质；2．用待定系数法求反比例函数的解析式；3．平移的性质．‎ ‎42．解：（1）过点M作MC⊥x轴，MD⊥y轴，‎ ‎∵AM=BM，∴点M为AB的中点。‎ ‎∵MC⊥x轴，MD⊥y轴，∴MC∥OB，MD∥OA。‎ ‎∴点C和点D分别为OA与OB的中点。‎ ‎∴MC=MD。则点M的坐标可以表示为（﹣a，a）。‎ 把M（﹣a，a）代入函数中，‎ 解得（负值舍去）。‎ ‎∴点M的坐标为（﹣，）。‎ ‎（2）∵则点M的坐标为（﹣，），∴MC=，MD=。‎ ‎∴OA=OB=2MC=，∴A（﹣，0），B（0，）。‎ 设直线AB的解析式为y=kx+b，‎ 把点A（﹣，0），B（0，）分别代入y=kx+b中得：‎ ‎，解得：。‎ ‎∴直线AB的解析式为 ‎【解析】‎ 试题分析：（1）过点M作MC⊥x轴，MD⊥y轴，根据M为AB的中点，MC∥OB，MD∥OA，利用平行线分线段成比例得到点C和点D分别为OA与OB的中点，从而得到MC=MD，设出点M的坐标代入反比例函数解析式中，求出a的值即可得到点M的坐标。‎ ‎（2）根据（1）中求出的点M的坐标得到MC与MD的长，从而求出OA与OB的长，得到点A与点B的坐标，设出一次函数的解析式，把点A与点B的坐标分别代入解析式中求出k与b的值，确定出直线AB的表达式。‎ ‎43．解：（1）把A（1，2）代入y=ax得a=2，‎ ‎∴正比例函数解析式为y=2x。‎ 把A（1，2）代入得b=1×2=2，‎ ‎∴反比例函数解析式为。‎ ‎（2）如图，当﹣1＜x＜0或x＞1时，正比例函数值大于反比例函数值。‎ ‎【解析】‎ 试题分析：（1）分别把A点坐标代入正比例函数解析式和反比例函数解析式，求出a与b的值，从而确定两函数解析式。‎ ‎（2）先画出y=2x和的图象，根据对称性得到两函数的另一个交点B与点A关于原点对称，则B点坐标为（﹣1，﹣2），然后观察图象得到当﹣1＜x＜0或x＞2时，正比例函数图象都在反比例函数图象上方，即正比例函数值大于反比例函数值。‎ ‎44．解：（1）如图，AD的长为ｘｍ，DC的长为ｙｍ，‎ 根据题意，得，即。‎ ‎∴ｙ与ｘ之间的函数关系式为。‎ ‎（2）由，且ｘ，ｙ都为正整数，‎ ‎∴ｘ可取1，2，3，4，5，6，10，12，15，20，30，60。‎ 但∵，‎ ‎∴符合条件的有：ｘ=5时，ｙ=12；ｘ=6时，ｙ=10；ｘ=10时，ｙ=6。‎ 答：满足条件的所有围建方案：AD=5ｍ，DC=12ｍ或AD=6ｍ，DC=10ｍ或AD=10ｍ，DC=6ｍ。‎ ‎【解析】（1）由面积为60ｍ2列式即可得ｙ与ｘ之间的函数关系式。‎ ‎（2）由和ｘ，ｙ都为正整数列举出所有ｘ值，根据得出符合条件的值即可。‎ ‎45．解：（1）将点A的横坐标1代入，得点A的纵坐标为3，∴A（1，3）。‎ 将A（1，3）代入，得，∴反比例函数解析式为。‎ 联立，解得或。∴B（3，1）。‎ ‎∵关于x的不等式的解集，就是的图象在的图象下方时x的取值范围，‎ ‎∴由函数图象知，关于x的不等式的解集为或。‎ ‎（2）存在。‎ 设A，AB的中点（即圆心）为M，则B，M。‎ 由勾股定理可求得：，‎ 若以AB为直径的圆经过点P（1，0），则，‎ 即，解得。‎ ‎∴。‎ ‎【解析】（1）根据直线解析式求A点坐标；根据A点在反比例函数的图象上，求出m的值，从而得到反比例函数关系式，与直线方程联立即可求得点B的坐标。因此，根据关于x的不等式的解集，就是的图象在的图象下方时x的取值范围即可求出结果。‎ ‎（2）根据圆心到点P的距离等于半径列式求解。‎ ‎46．解：（1）把点A（1，a）代入反比例函数（x＞0）得a=3，则A点坐标为（1，3）。‎ ‎（2）∵将△ABO沿x轴向右平移2个单位长度，得到Rt△DEF，‎ ‎∴D点坐标为（3，3）。‎ 把D（3，3）代入，得k=3×3=9。‎ ‎【解析】‎ 试题分析：（1）把点A（1，a）代入反比例函数可求出a，则可确定A点坐标。‎ ‎（2）根据平移的性质得到D点坐标为（3，3），然后把D（3，3）代入即可求出k。　‎ ‎47．解：（1）设y与x的函数关系式y=kx+b，由题意，得 ‎，解得：。‎ ‎∴y与x的函数关系式为：y=﹣4x+360。‎ ‎（2）由题意，得 W=y（x﹣40）﹣y=（﹣4x+360）（x﹣40）﹣（﹣4x+360）=﹣4x2+160x+360x﹣14400+4x﹣360‎ ‎=﹣4x2+524x﹣14760，‎ ‎∴w与x之间的函数关系式为：W=﹣4x2+524x﹣14760。‎ ‎∵W=﹣4（x2﹣131x）﹣14760=﹣4（x﹣65.5）2+2401，‎ 当x=65.5时，最大利润为2401元。‎ ‎∵x为整数，∴x=66或65时，W=2400元。‎ ‎∴x=65或66时，W最大=2400元。‎ ‎【解析】‎ 试题分析：（1）设y与x的函数关系式y=kx+b，根据售价与销量之间的数量关系建立方程组，求出其解即可。‎ ‎（2）根据利润=（售价﹣进价）×数量就可以表示出W，根据二次函数的性质求出最值。　‎ ‎48．解：（1）过A作AD⊥x轴，可得AD=1，‎ ‎∵C（2，0），即OC=2，∴AC=OC=。‎ 在Rt△ACD中，根据勾股定理得：CD=1。‎ ‎∴OD=OC+CD=2+1=3。∴A（3，1）。‎ 将A、C的坐标代入一次函数解析式得：‎ ‎，解得：。‎ ‎∴一次函数解析式为y=x﹣2。‎ 将A（3，1）代入反比例解析式得：k=3，‎ ‎∴反比例解析式为。‎ ‎（2）根据图形得：不等式ax+b≥的解集为﹣1≤x＜0或x≥3。‎ ‎【解析】‎ 试题分析：（1）过A作AD垂直于x轴，如图所示，由C的坐标求出OC的长，根据AC=OC求出AC的长，由A的纵坐标为1，得到AD=1，利用勾股定理求出CD的长，有OC+CD求出OD的长，确定出m的值，将A于与C坐标代入一次函数解析式求出a于b的值，即可得出一次函数解析式；将A坐标代入反比例函数解析式求出k的值，即可确定出反比例解析式。‎ ‎（2）将B坐标代入反比例解析式中求出n的值，确定出B坐标，利用图形即可得出所求不等式的解集：‎ 将B（﹣1，n）代入反比例解析式得：n=﹣3，即B（﹣1，﹣3）。‎ 根据图形得：不等式ax+b≥的解集为﹣1≤x＜0或x≥3。　‎ ‎49．解：（1）。‎ ‎（2）如图1，∵四边形BQNC是菱形，‎ ‎∴BQ=BC=NQ，∠BQC=∠NQC。‎ ‎∵AB⊥BQ，C是AQ的中点，∴BC=CQ=AQ。∴∠BQC=60°，∠BAQ=30°。‎ 在△ABQ和△ANQ中，∵，∴△ABQ≌△ANQ（SAS）。‎ ‎∴∠BAQ=∠NAQ=30°。∴∠BAO=30°。‎ ‎∵S四边形BQNC=，∴BQ=2。∴AB=BQ=。∴OA=AB=3。‎ 又∵P点在反比例函数的图象上，∴P点坐标为（3，2）。‎ ‎（3）∵OB=1，OA=3，∴AB=。‎ ‎∵△AOB∽△DBA，∴。∴BD=3。‎ ‎①如图2，当点Q在线段BD上，‎ ‎∵AB⊥BD，C为AQ的中点，∴BC=AQ。‎ ‎∵四边形BNQC是平行四边形，∴QN=BC，CN=BQ，CN∥BD。‎ ‎∴，∴BQ=CN=BD=。‎ ‎∴AQ=2。‎ ‎∴C四边形BQNC=。‎ ‎②如图3，当点Q在线段BD的延长线上，‎ ‎∵AB⊥BD，C为AQ的中点，‎ ‎∴BC=CQ=AQ。‎ ‎∴平行四边形BNQC是菱形，BN=CQ，BN∥CQ。‎ ‎∴。∴BQ=3BD=9。‎ ‎∴。‎ ‎∴C四边形BNQC=2AQ=。‎ ‎【解析】（1）根据同底等高的两个三角形的面积相等即可求出△PAB的面积。‎ ‎（2）首先求出∠BQC=60°，∠BAQ=30°，然后根据SAS证明△ABQ≌△ANQ，进而求出∠BAO=30°，由S四边形BQNC=求出OA=3，于是P点坐标求出。‎ ‎（3）分两类进行讨论，当点Q在线段BD上，根据题干条件求出AQ的长，进而求出四边形的周长，当点Q在线段考点：反比例函数综合题，曲线上点的坐标与方程的关系，菱形的性质，全等三角形的判定和性质，相似三角形的判定和性质，勾股定理，分类思想的应用。‎ BD的延长线上，依然根据题干条件求出AQ的长，再进一步求出四边形的周长。‎ ‎50．（1）y=（x＞0）（2）OA= C（5， ）（3）P1（， ），P2（﹣， ），P3（， ），P4（﹣， ）．‎ ‎【解析】（1）过点A作AH⊥OB于H，‎ ‎∵sin∠AOB=，OA=10，‎ ‎∴AH=8，OH=6，‎ ‎∴A点坐标为（6，8），根据题意得：‎ ‎8=，可得：k=48，‎ ‎∴反比例函数解析式：y=（x＞0）；‎ ‎（2）设OA=a（a＞0），过点F作FM⊥x轴于M，‎ ‎∵sin∠AOB=，‎ ‎∴AH=a，OH=a，‎ ‎∴S△AOH=•aa=a2，‎ ‎∵S△AOF=12，‎ ‎∴S平行四边形AOBC=24，‎ ‎∵F为BC的中点，‎ ‎∴S△OBF=6，‎ ‎∵BF=a，∠FBM=∠AOB，‎ ‎∴FM=a，BM=a，‎ ‎∴S△BMF=BM•FM=a•a=a2，‎ ‎∴S△FOM=S△OBF+S△BMF=6+a2，‎ ‎∵点A，F都在y=的图象上，‎ ‎∴S△AOH=k，‎ ‎∴a2=6+a2，‎ ‎∴a=，‎ ‎∴OA=，‎ ‎∴AH=，OH=2，‎ ‎∵S平行四边形AOBC=OB•AH=24，‎ ‎∴OB=AC=3，‎ ‎∴C（5， ）；‎ ‎（3）存在三种情况：‎ 当∠APO=90°时，在OA的两侧各有一点P，分别为：P1（， ），P2（﹣， ），‎ 当∠PAO=90°时，P3（， ），‎ 当∠POA=90°时，P4（﹣， ）．‎