2016宁波中考数学卷

2016宁波中考数学卷

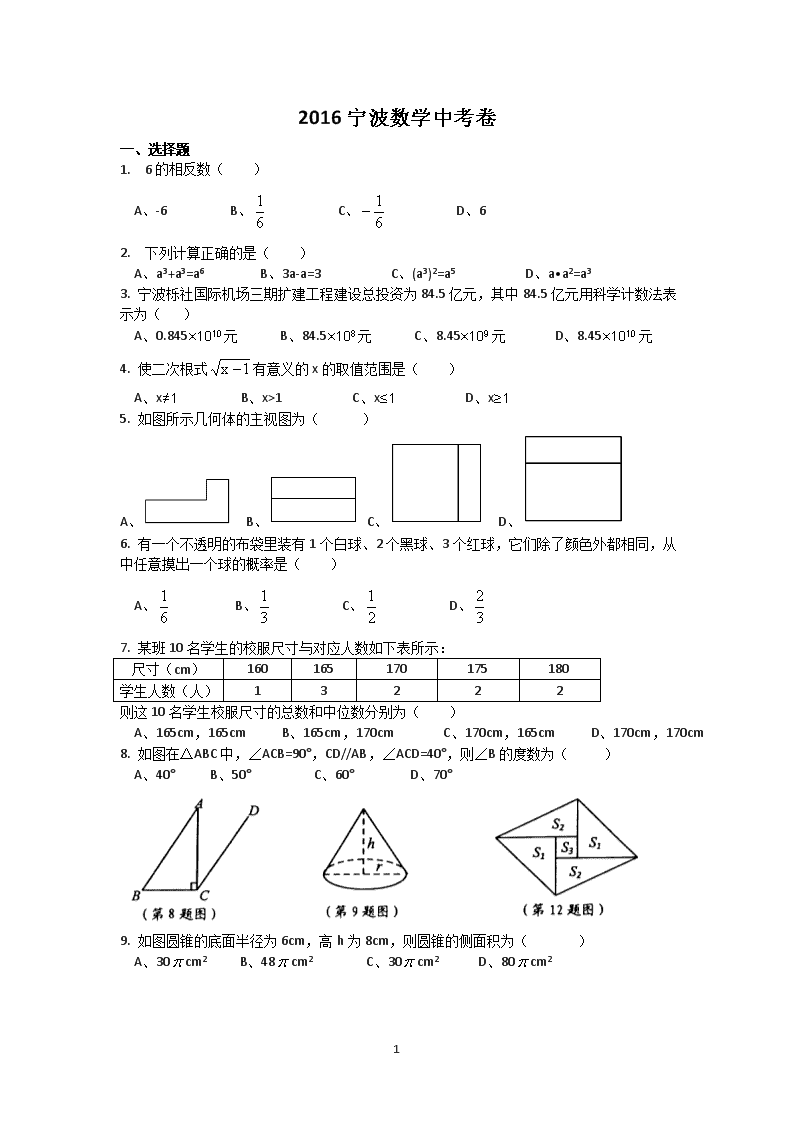
‎2016宁波数学中考卷 一、选择题 ‎1. 6的相反数（ ）‎ ‎ A、-6 B、 C、 D、6‎ 2. ‎ 下列计算正确的是（ ）‎ ‎ A、a3+a3=a6 B、3a-a=3 C、(a3)2=a5 D、a•a2=a3‎ 3. 宁波栎社国际机场三期扩建工程建设总投资为84.5亿元，其中84.5亿元用科学计数法表示为（ ）‎ 主视方向 ‎ A、0.845×1010元 B、84.5×108元 C、8.45×109元 D、8.45×1010元 4. 使二次根式有意义的x的取值范围是（ ）‎ ‎ A、x≠1 B、x>1 C、x≤1 D、x≥1‎ 5. 如图所示几何体的主视图为（ ） ‎ A、 B、 C、 D、‎ 6. 有一个不透明的布袋里装有1个白球、2个黑球、3个红球，它们除了颜色外都相同，从中任意摸出一个球的概率是（ ）‎ ‎ A、 B、 C、 D、‎ 7. 某班10名学生的校服尺寸与对应人数如下表所示：‎ 尺寸（cm）‎ ‎160‎ ‎165‎ ‎170‎ ‎175‎ ‎180‎ 学生人数（人）‎ ‎1‎ ‎3‎ ‎2‎ ‎2‎ ‎2‎ 则这10名学生校服尺寸的总数和中位数分别为（ ）‎ ‎ A、165cm，165cm B、165cm，170cm C、170cm，165cm D、170cm，170cm 8. 如图在△ABC中，∠ACB=90°，CD//AB，∠ACD=40°，则∠B的度数为（ ）‎ ‎ A、40° B、50° C、60° D、70°‎ 9. 如图圆锥的底面半径为6cm，高h为8cm，则圆锥的侧面积为（ ）‎ ‎ A、30cm2 B、48cm2 C、30cm2 D、80cm2 ‎ 6‎ 2. 能说明命题“对任何实数a，|a|>-a”是假命题的一个反例可以是（ ）‎ ‎ A、a=-2 B、a= C、a=-1 D、a=‎ 3. 已知函数y=ax2-2ax-1（a是常数，a≠0）,下列结论正确的是（ ）‎ ‎ A、当a=1时，函数图像经过（-1,1）‎ ‎ B、当a=-2时，函数图像与x轴没有交点 ‎ ‎ C、当a>0时，则当x≥1时，y随x的增大而减小 ‎ D、当a<0时，则当x≤1时，y随x的增大而增大 4. 如图是一个由5张纸拼接成的四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都是S1，另两张直角三角形纸片的面积都为S2，中间一张正方形的面积为S3，则这个平行四边形面积一定可以表示为（ ）‎ A、4S1 B、4S2 C、4S2+S3 D、3S1+4S3‎ 二、填空题 5. 实数-27的立方根是 ‎ 6. 分解因式：x2-xy= ‎ 7. 下列图案是用相同的火柴棍按一定规律拼搭而成，图案需要8根火柴棒，图案‚需要 ‎ 15根火柴棍，……按此规律，图案⑦需要 根火柴棍 8. 如图，在一次数学课外实践活动中，小聪在距离旗杆10m的A处测得旗杆顶端B的仰 ‎ 角为60°，测角仪高AD为1m，则旗杆高BC为 m（结果保留根号）‎ 9. 如图，半圆O的直径AB=2，弦CD//AB，∠COD=90°,则图中阴影部分的面积为 ‎ 10. 如图，点A为函数图像上一点，连接OA，交函数的图像于点B，点C是x轴上一点，且AO=AC,则△ABC的面积为 ‎ 三、解答题 11. 先化简，再求值：（x+1）（x-1）+x（3-x），其中x=2‎ 6‎ 2. 下列3×3网格图中都是由9个相同的小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：‎ （1） 选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形 （2） 选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形 （3） 选取2个涂上阴影，使5个阴影小正方形组成一个轴对称图形 ‎（请将三个小题依次作答在图1，图2，图3， 均只需要画出符合条件的一种情形）‎ 3. 为深化义务教育课程改革，某校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学、等多个类别的拓展性课程，要求每一位学生都自主选择一个类别的拓展性课程。为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：‎ 根据统计图中的信息，解答下列各题：‎ （1） 求本次被调查学生的人数 （2） 将条形统计图补充完整 （3） 若该校共有1600名学生，请估计是全校选择体育类的学生人数 6‎ 2. 已知抛物线与x轴交于A、B两点，与y轴交于点C，点B的坐标为（3,0）‎ ‎ （1）求m的值及抛物线的顶点坐标 ‎ （2）点P是抛物线对称轴上的一个动点，当PA+PC的值最小时，求点P的坐标。‎ 3. 如图，已知⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E。‎ （1） 求证：DE是⊙O的切线 （2） 求DE的长 6‎ 2. 某商场销售A,B两种品牌的教学设备，这两种教学设备的进价和售价如下表所示：‎ A B 进价（万元/套）‎ ‎1.5‎ ‎1.2‎ 售价（万元/套）‎ ‎1.65‎ ‎1.4‎ 该商场计划购进两种教学设备若干台，共需66万元，全部销售后可获毛利润9万元 ‎（毛利润=（售价-进价）×销售量）‎ （1） 该商场计划购进A,B两种品牌的教学设备各多少套？‎ （2） 通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量之多减少多少套 3. 从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成为两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另外一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线。‎ （1） 如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美 分割线.‎ （2） 在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数.‎ （3） 如图2，在△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长。‎ 6‎ 2. 如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（5,0），菱形OABC的顶点B，C都在第一象限，tan∠AOC=，将菱形绕点A按顺时针方向旋转，角α（0°<∠α<∠AOC）得到菱形FADE（点O的对应点为点F），EF与OC交于点G,连结AG:‎ （1） 求点B的坐标 （2） 当OG=4时，求AG的长 （3） 求证：GA平分∠OGE （4） 连结BD并延长交x轴于点P，当点P的坐标为（12,0）时，求点G的坐标。‎ 6‎