- 2021-05-13 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
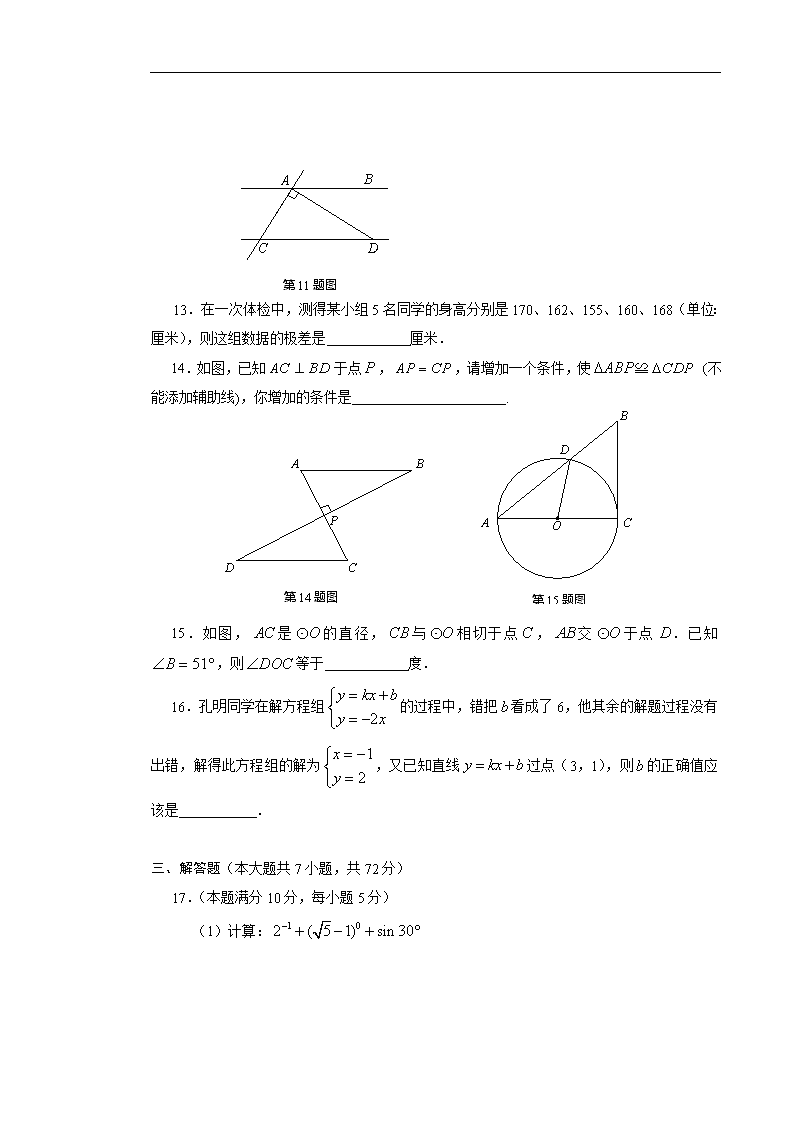
2009年湖南省株洲市初中毕业学业考试数学试题及答案
绝密★启用前 株洲市2009年初中毕业学业考试 数 学 试 题 卷 时量:120分钟 满分:120分 注意事项: 1.答题前,请按要求在答题卡上填写好自己的姓名、就读学校和准考证号。 2.答题时,切记答案要填在答题卡上,答在试题卷上的答案无效。 3.考试结束后,请将试题卷和答题卡都交给监考老师。 一、选择题(每小题有且只有一个正确答案,本题共8小题,每小题3分,共24分) 1.的相反数是 A. B. C. D. 2.若使二次根式在实数范围内有意义,则x的取值范围是 A. B. C. D. 3.下列四个图形中,不是轴对称图形的是 A. B. C. D. 4.一次函数的图象不经过 A.第一象限 B.第二象限 C.第三象限 D.第四象限 5.估计的运算结果应在 A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间 6.从分别写有数字、、、、、、、、的九张一样的卡片中,任意抽取一张卡片,则所抽卡片上数字的绝对值小于2的概率是 A. B. C. D. 第7题图 7.如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四个完全相同的四边形拼成的.测得,,,,则的度数是 A. B. C. D. 8.定义:如果一元二次方程满足,那么我们称这个方程为“凤凰”方程. 已知 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 A. B. C. D. 二、填空题(本题共8小题,每小题3分,共24分) 9.分解因式: . 10.孔明同学买铅笔支,每支0.4元,买练习本本,每本2元.那么他买铅笔和练习本一共花了 元. 11.如图,,,,则的度数是 . y 第12题图 O x 1 2 P(1,2) · 12.反比例函数图象如图所示,则这个反比例函数的解析式是 . 第11题图 13.在一次体检中,测得某小组5名同学的身高分别是170、162、155、160、168(单位:厘米),则这组数据的极差是 厘米. 第15题图 14.如图,已知于点,,请增加一个条件,使≌ (不能添加辅助线),你增加的条件是 . 第14题图 15.如图,是的直径,与相切于点,交于点.已知 ,则等于 度. 16.孔明同学在解方程组的过程中,错把看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线过点(3,1),则的正确值应该是 . 三、解答题(本大题共7小题,共72分) 17.(本题满分10分,每小题5分) (1)计算: (2)先化简,再求值:,其中. 18.(本题满分10分)如图,在中,,,将绕点沿逆时针方向旋转得到. (1)线段的长是 , 的度数是 ; (2)连结,求证:四边形是平行四边形; (3)求四边形的面积. 小学生 20% 大学生 10% 初中生? 高中生30% 19.(本题满分10分)某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图. (1)参加这次夏令营活动的初中生共有多少人? (2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款. 结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,问平均每人捐款是多少元? (3)在(2)的条件下,把每个学生的捐款数额(以元为单位)一一记录下来,则在这组数据中,众数是多少? 20.(本题满分10分)初中毕业了,孔明同学准备利用暑假卖报纸赚取140~200元钱,买一份礼物送给父母.已知:在暑假期间,如果卖出的报纸不超过1000份,则每卖出一份报纸可得0.1元;如果卖出的报纸超过1000份,则超过部分每份可得0.2元. (1)请说明:孔明同学要达到目的,卖出报纸的份数必须超过1000份. (2)孔明同学要通过卖报纸赚取140~200元,请计算他卖出报纸的份数在哪个范围内. 21.(本题满分10分)如图,点、、是上的三点,. (1)求证:平分. (2)过点作于点,交于点. 若,,求的长. 22.(本题满分10分)如图1,中,,,点在线段上运动,点、分别在线段、上,且使得四边形是矩形.设的长为,矩形的面积为,已知是的函数,其图象是过点(12,36)的抛物线的一部分(如图2所示). (1)求的长; (2)当为何值时,矩形的面积最大,并求出最大值. 为了解决这个问题,孔明和研究性学习小组的同学作了如下讨论: 张明:图2中的抛物线过点(12,36)在图1中表示什么呢? 李明:因为抛物线上的点是表示图1中的长与矩形面积的对应关系,那么,(12,36)表示当时,的长与矩形面积的对应关系. 赵明:对,我知道纵坐标36是什么意思了! 孔明:哦,这样就可以算出,这个问题就可以解决了. 请根据上述对话,帮他们解答这个问题. O 图1 图2 23.(本题满分12分)如图,已知为直角三角形,,,点、在轴上,点坐标为(,)(),线段与轴相交于点,以(1,0)为顶点的抛物线过点、. (1)求点的坐标(用表示); (2)求抛物线的解析式; (3)设点为抛物线上点至点之间的一动点,连结并延长交于点,连结 并延长交于点,试证明:为定值. 再次提醒:所有的答案都填(涂)到答题卡上,答在本卷上的答案无效。 株洲市2009年初中毕业学业考试试卷 数学参考答案及评分标准 一、选择题: 题 次 1 2 3 4 5 6 7 8 答 案 B A D D C B B A 二、填空题: 9. 10. 11. 12. 13.15 14.或或或或 15. 16. 三、解答题: 17.(1)原式= ……3分 (2)化简,得:原式= …… 3分 ……5分 当时,得:原式 …… 5分 18.(1)6,135°……4分 (2) ∴ 又 ∴四边形是平行四边形……8分 (3) 36 ……10分 19.(1)80 …… 3分 (2)11.5元 ……8分 (3)10元 ……10分 20.(1)如果孔明同学卖出1000份报纸,则可获得:元,没有超过140元,从而不能达到目的.(注:其它说理正确、合理即可.) ……… 3分 (2)设孔明同学暑假期间卖出报纸份,由(1)可知,依题意得: ………………………7分 解得 ……………………9分 答:孔明同学暑假期间卖出报纸的份数在1200~1500份之间. ……………………10分 21.(1)∵, ∴;∵,∴ ∴ 即平分. ………………………5分(2)∵ ∴ 又,∴∴, ∴,设,则,根据勾股定理得,解得(或者用) 即的长是. ………………………10分 22.(1)当时, ∴, 又在中,,∴ ∴ ∴ ……………4分 (2)解法一:若 ,则,,∴,整理得 ………………… 9分 ∴ 当时,. ………………… 10分 解法二:由,结合图象可知抛物线经过点(0,0)、(16,0)、(12,36),可设抛物线解析式为,将(12,36)代入求得,∴,整理得,∴ 当时,. ………………… 10分 解法三:由,结合图象可知抛物线经过点(0,0)、(16,0),知抛物线对称轴为,∴抛物线顶点的横坐标为8.∴当时,矩形的面积最大,此时,,∴,∴最大面积为48. …………………… 10分 23.(1)由可知,,又△ABC为等腰直角三角形,∴,,所以点A的坐标是(). ………………… 3分 (2)∵ ∴,则点的坐标是(). 又抛物线顶点为,且过点、,所以可设抛物线的解析式为:,得: 解得 ∴抛物线的解析式为 ………7分 (3)过点作于点,过点作于点,设点的坐标是,则,. ∵ ∴∽ ∴ 即,得 ∵ ∴∽ ∴ 即,得 又∵ ∴ 即为定值8. ……………………12分 本答案仅供参考,若有其他解法,请参照本评分标准评分.查看更多