- 2021-05-13 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届中考数学全程演练 第一部分 第五单元第14课时 一次函数(正比例函数)的图象与性质
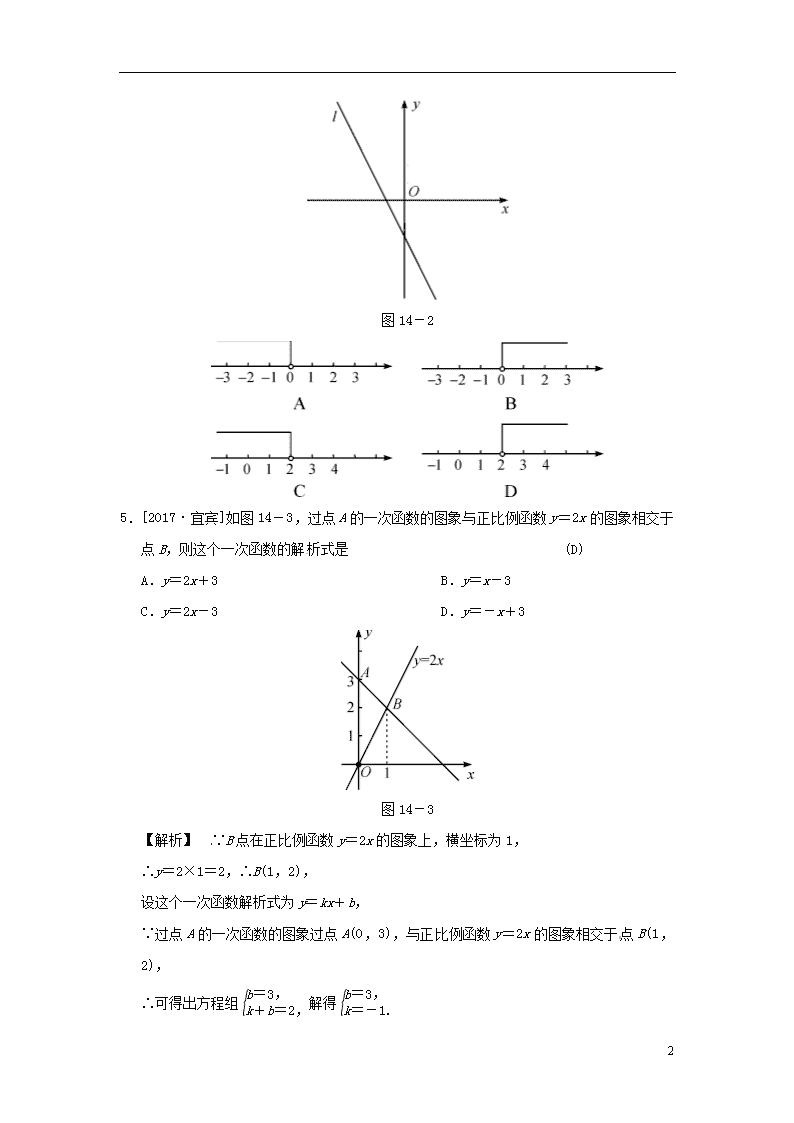
第14课时 一次函数(正比例函数)的图象与性质 (60分) 一、选择题(每题5分,共30分) 1.[2016·遂宁]直线y=2x-4与y轴的交点坐标是 (D) A.(4,0) B.(0,4) C.(-4,0) D.(0,-4) 2.[2016·怀化]一次函数y=kx+b(k≠0)在平面直角坐标系内的图象如图14-1所示,则k和b的取值范围是 (C) A.k>0,b>0 B.k<0,b<0 C.k<0,b>0 D.k>0,b<0 图14-1 3.[2016·广安]某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为x km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是(D) A.y=0.12x,x>0 B.y=60-0.12x,x>0 C.y=0.12x,0≤x≤500 D.y=60-0.12x,0≤x≤500 【解析】 因为油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了, 可得×60÷100=0.12 L/km,60÷0.12=500 km, 所以y与x之间的函数解析式和自变量取值范围是y=60-0.12x(0≤x≤500). 4.[2017·河北]如图14-2,直线l经过第二、三、四象限,l的解析式是y=(m-2)x+n,则m的取值范围在数轴上表示为 (C) 7 图14-2 5.[2017·宜宾]如图14-3,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是 (D) A.y=2x+3 B.y=x-3 C.y=2x-3 D.y=-x+3 图14-3 【解析】 ∵B点在正比例函数y=2x的图象上,横坐标为1, ∴y=2×1=2,∴B(1,2), 设这个一次函数解析式为y=kx+b, ∵过点A的一次函数的图象过点A(0,3),与正比例函数y=2x的图象相交于点B(1,2), ∴可得出方程组解得 7 则这个一次函数的解析式为y=-x+3, 6.[2016·巴中]小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(m)与时间t(min)之间关系的大致图象是 (B) 【解析】 根据题中信息可知,相同的路程,跑步比慢步的速度快;在一定时间内没有移动距离,则路程为0.故小华的爷爷跑步到公园的速度最快,即单位时间内通过的路程最大,打太极的过程中没有移动距离,因此通过的路程为0,还要注意出去和回来时的方向不同,故B符合要求. 二、填空题(每题5分,共20分) 7.[2016·连云港]已知一个函数,当x>0时,函数值y随着x的增大而减小,请写出这个函数关系式(写出一个即可)__y=-x+2,y=,y=-x2+1等__. 8.[2016·天津]若一次函数y=2x+b(b为常数)的图象经过点(1,5),则b的值为__3__. 【解析】 把点(1,5)代入y=2x+b,得5=2×1+b, 解得b=3. 9.[2016·永州]已知一次函数y=kx+b的图象经过两点A(0,1),B(2,0),则当x__≥2__时,y≤0. 【解析】 ∵一次函数y=kx+b的图象经过两点A(0,1),B(2,0), ∴解得 这个一次函数的表达式为y=-x+1. 解不等式-x+1≤0,解得x≥2. 10.[2017·株洲]直线y=k1x+b1(k1>0)与y=k2x+b2相交于点(-2,0),且两直线与y轴围成的三角形面积为4,那么b1-b2等于__4__. 第10题答图 【解析】 如答图,直线y=k1x+b1(k1>0)与y轴交于B点,则OB=b1,直线y=k2x+b2(k2<0)与y 7 轴交于C,则OC=-b2, ∵△ABC的面积为4, ∴OA·OB+OA·OC=4, ∴×2·b1+×2(-b2)=4, 解得b1-b2=4. 三、解答题(10分) 11.(10分)已知一次函数y=kx+b的图象经过(0,2),(1,3)两点. (1)求k,b的值; (2)若一次函数y=kx+b的图象与x轴的交点为A(a,0),求a的值. 【解析】 (1)运用待定系数法求k,b; (2)由函数图象的意义求a. 解:(1)将(0,2),(1,3)两点的坐标代入一次函数y=kx+b的解析式,得解得 ∴k,b的值分别是1,2; (2)由(1)得y=x+2,令y=0,得x=-2,即a=-2. (32分) 12.(4分)[2016·潍坊]若式子+(k-1)0有意义,则一次函数y=(k-1)x+1-k的图象可能是 (A) 【解析】 ∵式子+(k-1)0有意义, ∴解得k>1, 7 ∵k-1>0,∴1-k<0, ∴一次函数y=(k-1)x+1-k的图象可能是A选项所示图象. 13.(4分)已知直线y=-x+(n为正整数)与两坐标轴围成的三角形的面积为Sn,则S1+S2+S3+…+S2 012=____. 【解析】 令x=0,则y=, 令y=0,则-x+=0,解得x=, 所以Sn=××=, 所以S1+S2+S3+…+S2 012 =× =×=×=. 故答案为. 14.(4分)[2017·巴中]如图14-4,已知直线y=-x+4与x轴,y轴分别交于A,B两点,把△AOB绕点A按顺时针方向旋转90°后得到△AO1B1,则点B1的坐标是__(7,3)__. 图14-4 【解析】 直线y=-x+4与x轴,y轴分别交于A(3,0),B(0,4)两点, 旋转前后三角形全等, 由图易知点B1的纵坐标为OA长,即为3, 横坐标为OA+OB=3+4=7. 15.(10分)已知点P(x,y)是第一象限内的点,且x+y=8,点A的坐标为(10,0),设△OAP的面积为S. (1)求S与x的函数关系式,并写出自变量的取值范围; (2)画出S与x的函数图象. 【解析】 (1)先确定x,y的符号,再由S=OA·y,得S=OA·(8-x). 由确定取值范围, 7 (2)描出x轴,y轴上的两点即可连线. 解:(1)∵P(x,y)在第一象限内, ∴x>0,y>0. ∵x+y=8,∴y=8-x, ∴S=OA·y=×10×(8-x), 即S=40-5x(0<x<8); (2)如答图所示. 第15题答图 16.(10分)[2016·绍兴]小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏 离家的路程y(m)和所经过的时间x(min)之间的函数图象如图14-5所示.请根据图象回答下列问题: (1)小敏去超市途中的速度是多少?在超市逗留了多少时间? (2)小敏几点几分返回到家? 图14-5 解:(1)小敏去超市途中的速度是3 000÷10=300(m/min), 在超市逗留了的时间为40-10=30(min); (2)设返回家时,y与x的函数解析式为y=kx+b, 把(40,3 000),(45,2 000)代入得 7 解得 ∴函数解析式为y=-200x+11 000, 当y=0时,x=55, ∴返回到家的时间为8:55. (8分) 17.(8分)在平面直角坐标系中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,AnBnCnCn-1按如图14-6所示的方式放置,其中点A1,A2,A3,…,An均在一次函数y=kx+b的图象上,点C1,C2,C3,…,Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为__(2n-1-1,2n-1)__. 图14-6 7查看更多