上海市中考数学模拟试题压轴题分析11宝山25

上海市中考数学模拟试题压轴题分析11宝山25

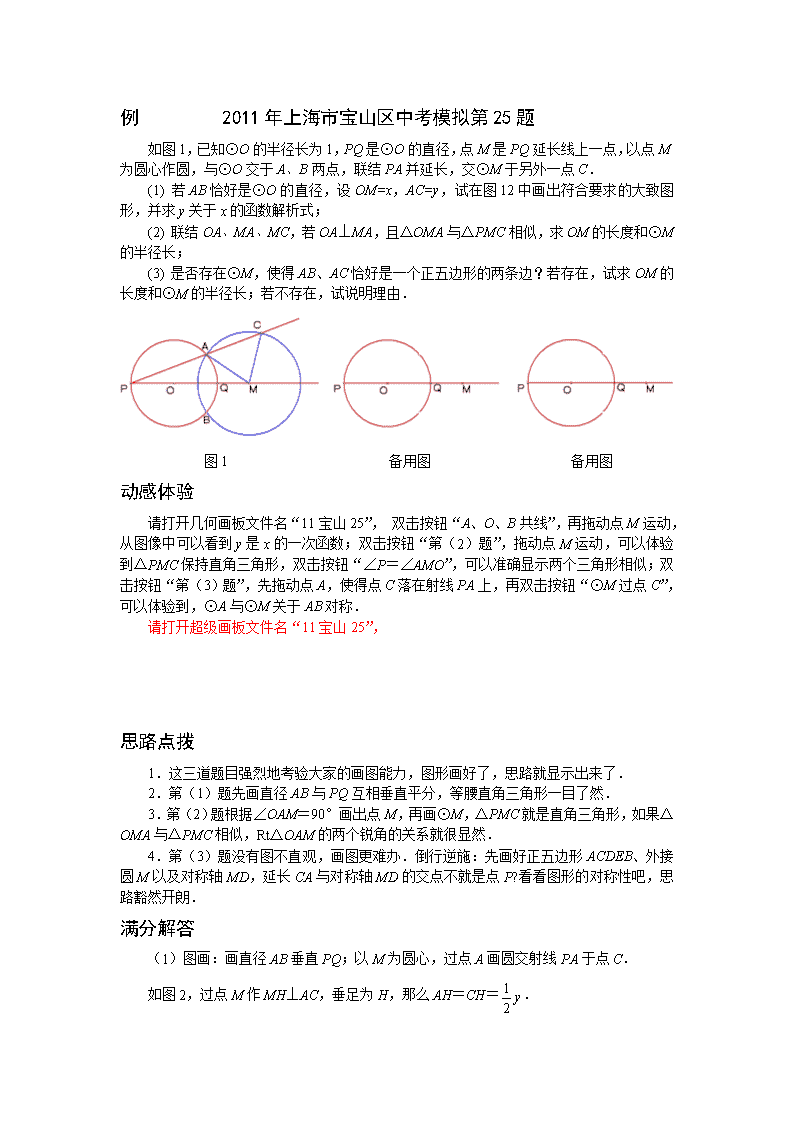
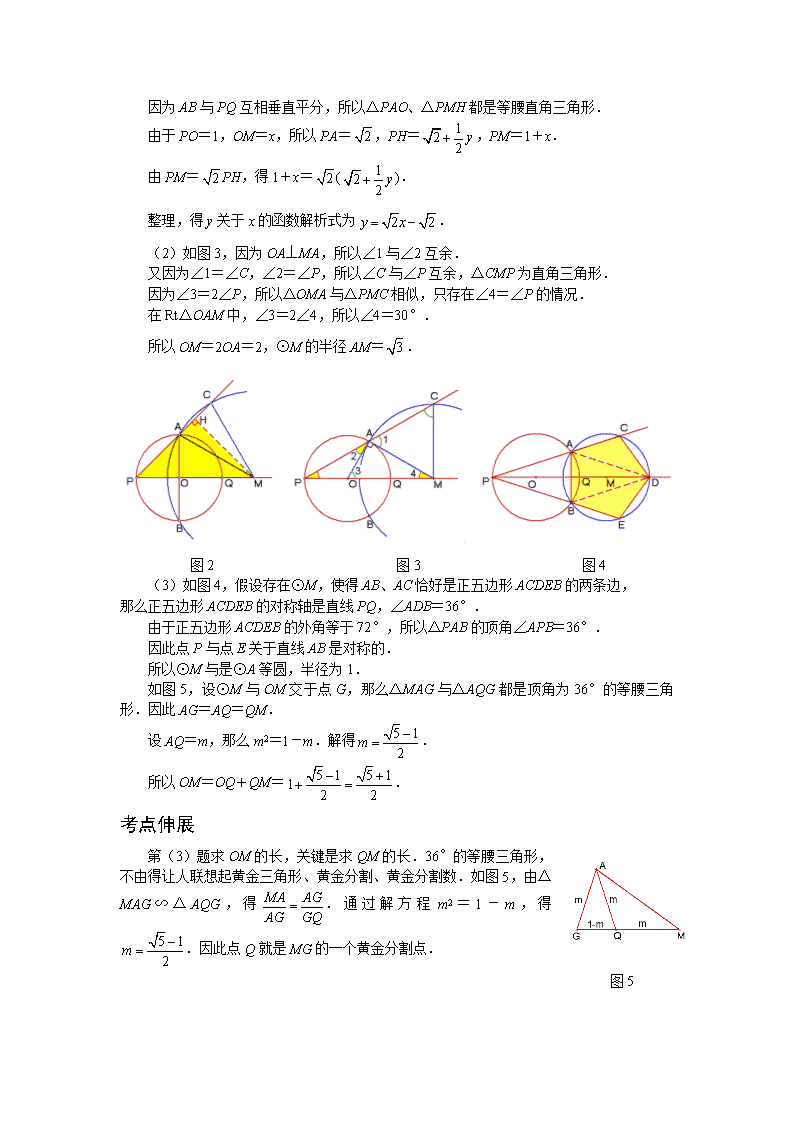
例 2011年上海市宝山区中考模拟第25题 如图1，已知⊙O的半径长为1，PQ是⊙O的直径，点M是PQ延长线上一点，以点M为圆心作圆，与⊙O交于A、B两点，联结PA并延长，交⊙M于另外一点C．‎ ‎(1) 若AB恰好是⊙O的直径，设OM=x，AC=y，试在图12中画出符合要求的大致图形，并求y关于x的函数解析式；‎ ‎(2) 联结OA、MA、MC，若OA⊥MA，且△OMA与△PMC相似，求OM的长度和⊙M的半径长；‎ ‎(3) 是否存在⊙M，使得AB、AC恰好是一个正五边形的两条边？若存在，试求OM的长度和⊙M的半径长；若不存在，试说明理由．‎ 图1 备用图 备用图 动感体验 请打开几何画板文件名“11宝山25”， 双击按钮“A、O、B共线”，再拖动点M运动，从图像中可以看到y是x的一次函数；双击按钮“第（2）题”，拖动点M运动，可以体验到△PMC保持直角三角形，双击按钮“∠P＝∠AMO”，可以准确显示两个三角形相似；双击按钮“第（3）题”，先拖动点A，使得点C落在射线PA上，再双击按钮“⊙M过点C”，可以体验到，⊙A与⊙M关于AB对称．‎ 请打开超级画板文件名“11宝山25”，‎ 思路点拨 ‎1．这三道题目强烈地考验大家的画图能力，图形画好了，思路就显示出来了．‎ ‎2．第（1）题先画直径AB与PQ互相垂直平分，等腰直角三角形一目了然．‎ ‎3．第（2）题根据∠OAM＝90°画出点M，再画⊙M，△PMC就是直角三角形，如果△OMA与△PMC相似，Rt△OAM的两个锐角的关系就很显然．‎ ‎4．第（3）题没有图不直观，画图更难办．倒行逆施：先画好正五边形ACDEB、外接圆M以及对称轴MD，延长CA与对称轴MD的交点不就是点P?看看图形的对称性吧，思路豁然开朗．‎ 满分解答 ‎（1）图画：画直径AB垂直PQ；以M为圆心，过点A画圆交射线PA于点C．‎ 如图2，过点M作MH⊥AC，垂足为H，那么AH＝CH＝．‎ 因为AB与PQ互相垂直平分，所以△PAO、△PMH都是等腰直角三角形．‎ 由于PO＝1，OM＝x，所以PA＝，PH＝，PM＝1＋x．‎ 由PM＝PH，得1＋x＝()．‎ 整理，得y关于x的函数解析式为．‎ ‎（2）如图3，因为OA⊥MA，所以∠1与∠2互余．‎ 又因为∠1＝∠C，∠2＝∠P，所以∠C与∠P互余，△CMP为直角三角形．‎ 因为∠3＝2∠P，所以△OMA与△PMC相似，只存在∠4＝∠P的情况．‎ 在Rt△OAM中，∠3＝2∠4，所以∠4＝30°．‎ 所以OM＝2OA＝2，⊙M的半径AM＝．‎ 图2 图3 图4‎ ‎（3）如图4，假设存在⊙M，使得AB、AC恰好是正五边形ACDEB的两条边，‎ 那么正五边形ACDEB的对称轴是直线PQ，∠ADB＝36°．‎ 由于正五边形ACDEB的外角等于72°，所以△PAB的顶角∠APB＝36°．‎ 因此点P与点E关于直线AB是对称的．‎ 所以⊙M与是⊙A等圆，半径为1．‎ 如图5，设⊙M与OM交于点G，那么△MAG与△AQG都是顶角为36°的等腰三角形．因此AG＝AQ＝QM．‎ 设AQ＝m，那么m2＝1－m．解得．‎ 所以OM＝OQ＋QM＝．‎ 考点伸展 第（3）题求OM的长，关键是求QM的长．36°的等腰三角形，不由得让人联想起黄金三角形、黄金分割、黄金分割数．如图5，由△MAG∽△AQG，得．通过解方程m2＝1－m，得．因此点Q就是MG的一个黄金分割点．‎ ‎ 图5‎