中考数学压轴题精选2及答案

中考数学压轴题精选2及答案

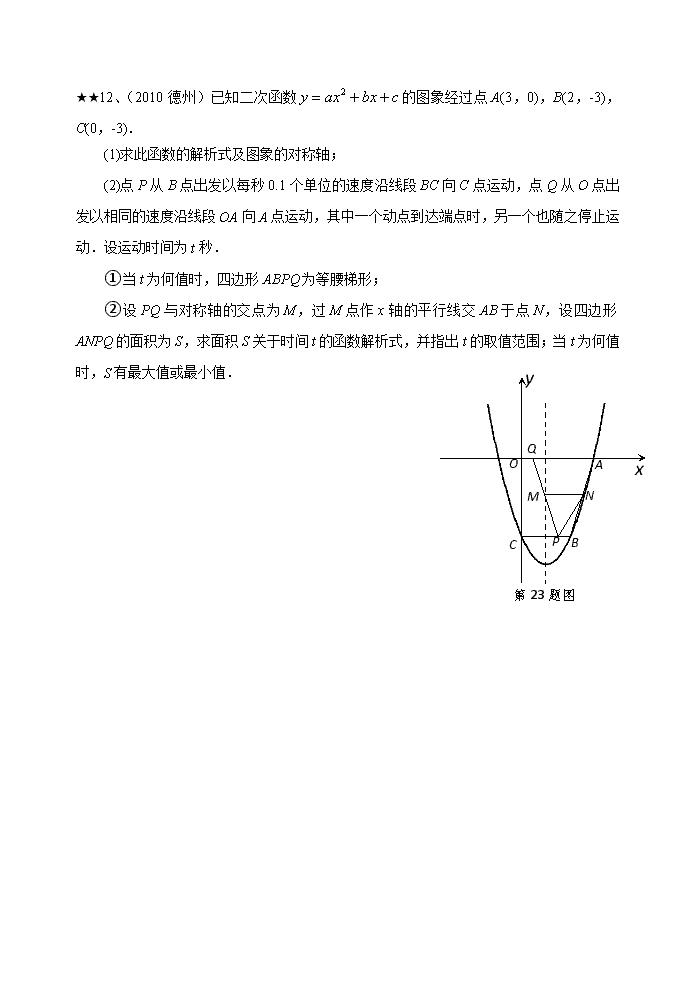
‎★★11、（2010德化）如图1，已知抛物线经过坐标原点O和x轴上另一点E，顶点M的坐标为 (2,4)；矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3.‎ ‎（1）求该抛物线的函数关系式；‎ ‎（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）. ‎ ‎① 当t=时，判断点P是否在直线ME上，并说明理由；‎ 图2‎ B C O A D E M y x P N ‎·‎ 图1‎ B C O ‎(A)‎ D E M y x ‎② 设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．‎ ‎★★12、（2010德州）已知二次函数的图象经过点A(3，0)，B(2，-3)，C(0，-3)．‎ ‎(1)求此函数的解析式及图象的对称轴；‎ ‎(2)点P从B点出发以每秒0.1个单位的速度沿线段BC向C点运动，点Q从O点出发以相同的速度沿线段OA向A点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t秒．‎ ‎①当t为何值时，四边形ABPQ为等腰梯形；‎ x y O A B C P Q M N 第23题图 ‎②设PQ与对称轴的交点为M，过M点作x轴的平行线交AB于点N，设四边形ANPQ的面积为S，求面积S关于时间t的函数解析式，并指出t的取值范围；当t为何值时，S有最大值或最小值．‎ ‎★★13、（2010东阳）如图，P为正方形ABCD的对称中心，A（0，3），B（1，0），直线OP交AB于N，DC于M，点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动，同时，点R从O出发沿OM方向以个单位每秒速度运动，运动时间为t。求：‎ ‎（1）C的坐标为 ▲ ；‎ C O A B D N M P x y R H ‎（2）当t为何值时，△ANO与△DMR相似？‎ ‎（3）△HCR面积S与t的函数关系式；‎ 并求以A、B、C、R为顶点的四边形是梯形 时t的值及S的最大值。‎ ‎★★14、（2010恩施）如图11，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，-3）点，点P是直线BC下方的抛物线上一动点.‎ ‎（1）求这个二次函数的表达式．‎ ‎（2）连结PO、PC，并把△POC沿CO翻折，得到四边形POPC， 那么是否存在点P，使四边形POPC为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．‎ ‎（3）当点P运动到什么位置时，四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.‎ ‎★★15、（2010广安）如图，直线y = -x-1与抛物线y=ax2+bx-4都经过点A(-1, 0)、B(3, -4)．‎ ‎（1）求抛物线的解析式；‎ ‎（2）动点P在线段AC上，过点P作x轴的垂线与抛物线相交于点E，求线段PE长度的最大值；‎ ‎（3）当线段PE的长度取得最大值时，在抛物线上是否存在点Q，使△PCQ是以PC为直角边的直角三角形?若存在，请求出Q点的坐标；若不存在．请说明理由．‎ ‎ ‎ ‎★★16、（2010广州）如图，⊙O的半径为1，点P是⊙O上一点，弦AB垂直平分线段OP，点D是上任一点（与端点A、B不重合），DE⊥AB于点E，以点D为圆心、DE长为半径作⊙D，分别过点A、B作⊙D的切线，两条切线相交于点C．‎ ‎（1）求弦AB的长；‎ ‎（2）判断∠ACB是否为定值，若是，求出∠ACB的大小；否则，请说明理由；‎ C P D O B A E ‎（3）记△ABC的面积为S，若＝4，求△ABC的周长.‎ ‎17.（2010广东广州）如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线＝－＋交折线OAB于点E．‎ ‎（1）记△ODE的面积为S，求S与的函数关系式；‎ C D B A E O ‎（2）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B‎1C1，试探究OA1B‎1C1与矩形OABC的重叠部分的面积是否发生变化，若不变，求出该重叠部分的面积；若改变，请说明理由.‎ ‎★★19、（2010杭州）在平面直角坐标系xOy中，抛物线的解析式是y =+1，‎ 点C的坐标为(–4，0)，平行四边形OABC的顶点A，B在抛物 线上，AB与y轴交于点M，已知点Q(x，y)在抛物线上，点 P(t，0)在x轴上. ‎ ‎ (1) 写出点M的坐标； ‎ ‎ (2) 当四边形CMQP是以MQ，PC为腰的梯形时.‎ ‎① 求t关于x的函数解析式和自变量x的取值范围；‎ ‎② 当梯形CMQP的两底的长度之比为1：2时，求t的值.‎ ‎（第24题）‎ ‎★★18、（2010桂林）如图，过A（8，0）、B（0，）两点的直线与直线交于点C．平行于轴的直线从原点O出发，以每秒1个单位长度的速度沿轴向右平移，到C点时停止；分别交线段BC、OC于点D、E，以DE为边向左侧作等边△DEF，设△DEF与△BCO重叠部分的面积为S（平方单位），直线的运动时间为t（秒）．‎ ‎（1）直接写出C点坐标和t的取值范围； ‎ ‎（2）求S与t的函数关系式；‎ ‎（3）设直线与轴交于点P，是否存在这样的点P，使得以P、O、F为顶点的三角形为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．‎ ‎★★20、（2010红河州）如图9，在直角坐标系xoy中，O是坐标原点，点A在x正半轴上，OA=cm，点B在y轴的正半轴上，OB=‎12cm，动点P从点O开始沿OA以cm/s的速度向点A移动，动点Q从点A开始沿AB以‎4cm/s的速度向点B移动，动点R从点B开始沿BO以‎2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动，移动时间为t（0＜t＜6）s.‎ ‎（1）求∠OAB的度数.‎ ‎（2）以OB为直径的⊙O‘与AB交于点M，当t为何值时，PM与⊙O‘相切？‎ ‎（3）写出△PQR的面积S随动点移动时间t的函数关系式，并求s的最小值及相应的t值.‎ ‎（4）是否存在△APQ为等腰三角形，若存在，求出相应的t值，若不存在请说明理由.‎