2009年山东省济宁市高中阶段学校招生考试试题及答案

2009年山东省济宁市高中阶段学校招生考试试题及答案

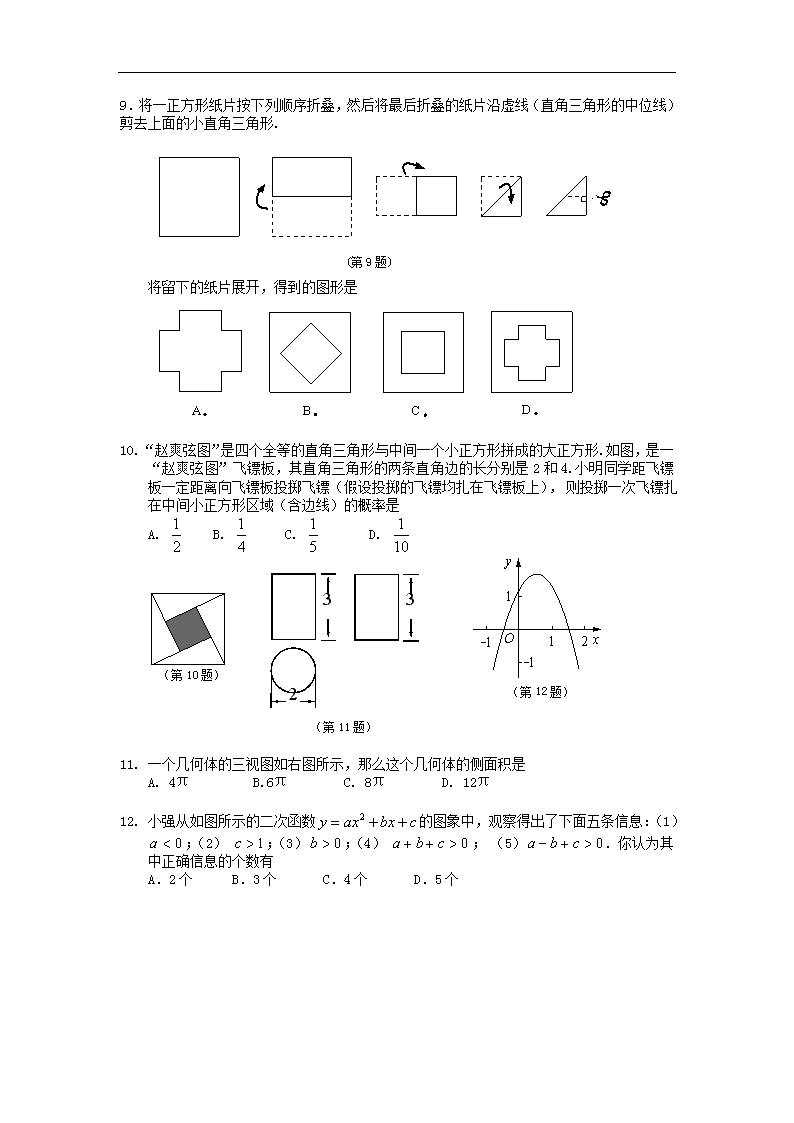
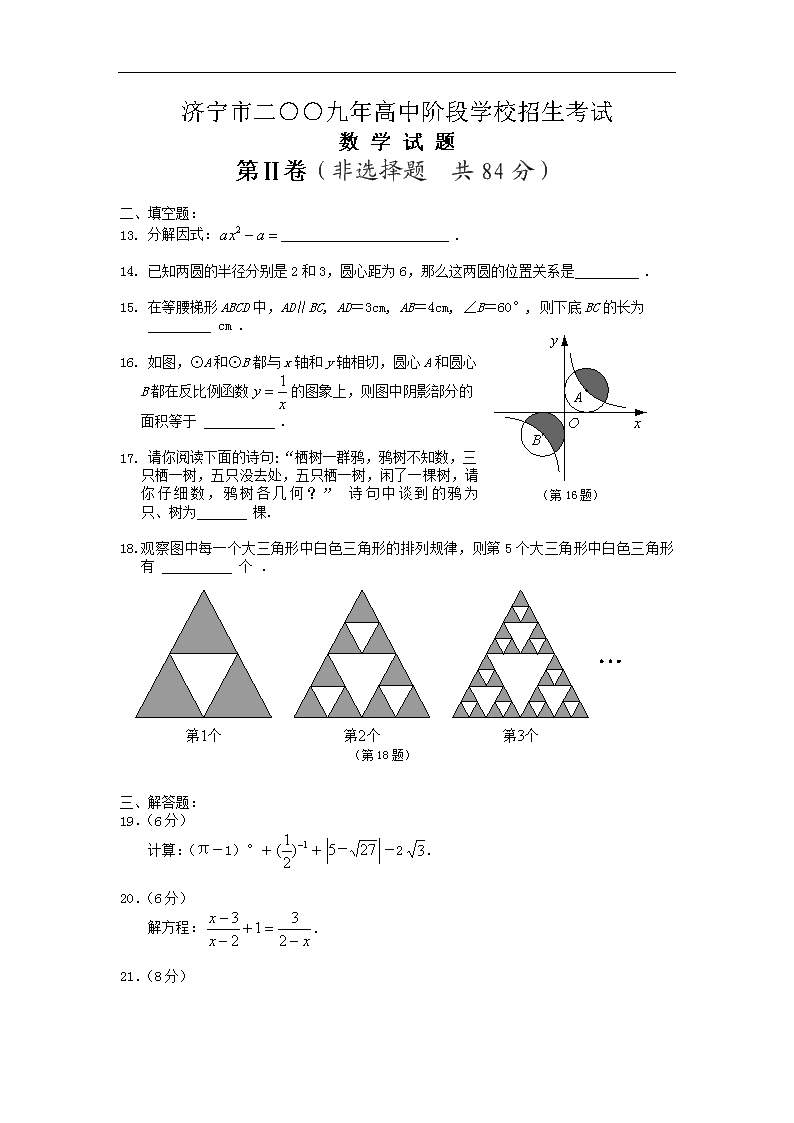
济宁市二○○九年高中阶段学校招生考试 数 学 试 卷 注意事项:‎ ‎1.本试题分第Ⅰ卷和第Ⅱ卷两部分，共10页.第Ⅰ卷2页为选择题，36分，第Ⅱ卷8页为非选择题，84分；共120分.考试时间为120分钟.‎ ‎2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上．每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，必须先用橡皮擦干净，再改涂其他答案．‎ ‎3．答第Ⅱ卷时，将密封线内的项目填写清楚，并将座号填写在第8页右侧，用钢笔或圆珠笔直接答在试卷上．考试结束，试题和答题卡一并收回．‎ 第Ⅰ卷（选择题　共36分）‎ 一、选择题（下列各题的四个选项中，只有一顶符合题意，每小题3分，共36分）‎ ‎1. 2的倒数是 ‎(第2题)‎ ‎ A. B. － C. 2 D.－2 ‎ ‎ ‎ ‎2. 如图，△ABC中，∠A＝70°，∠B＝60°，点D在BC的延长 线上， 则∠ACD等于 ‎ A. 100° B. 120° C. 130° D. 150°‎ ‎ ‎ ‎3．下列运算中，正确的是 A． B． C． D． ‎ ‎ ‎ ‎4. 山东省地矿部门经过地面磁测，估算济宁磁异常铁矿的内蕴经济资源量为 ‎10 800 000 000吨. 这个数据用科学记数法表示为 ‎ A. 108×10 8吨 B. 10 .8×10 9吨 ‎ C. 1 .08×10 10吨 D. 1 .08×10 11吨 ‎5. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）‎ A． B． C． D． ‎ ‎ (第5题)‎ ‎6. 在函数中，自变量x的取值范围是 A、x≠0 B、x＞‎3 C、x ≠ －3 D、x≠3 ‎ ‎（第7题）‎ ‎7. 如图，在长为‎8 cm、宽为‎4 cm的矩形中，截去一个矩形，使得留下 的矩形（图中阴影部分）与原矩形相似，则留下矩形的面积是（ ）‎ ‎ A. ‎2 cm2 B. ‎4 cm2 C. ‎8 cm2 D. ‎16 cm2‎ ‎ ‎ ‎8. 已知为实数，那么等于 A. B. C. － 1 D. 0‎ ‎9．将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线（直角三角形的中位线）剪去上面的小直角三角形.‎ ‎(第9题)‎ 将留下的纸片展开，得到的图形是 ‎10.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4.小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上）, 则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是 ‎（第12题）‎ ‎ A. B. C. D. ‎ ‎（第11题）‎ ‎3‎ ‎2‎ ‎3‎ ‎（第10题）‎ ‎11. 一个几何体的三视图如右图所示，那么这个几何体的侧面积是 ‎ A. 4π B.6π C. 8π D. 12π ‎ ‎ ‎12. 小强从如图所示的二次函数的图象中，观察得出了下面五条信息：（1）；（2） ；（3）；（4） ； （5）. 你认为其中正确信息的个数有 A．2个 B．3个 C．4个 D．5个 济宁市二○○九年高中阶段学校招生考试 数 学 试 题 第Ⅱ卷（非选择题　共84分）‎ 二、填空题：‎ ‎13. 分解因式： .‎ ‎14. 已知两圆的半径分别是2和3，圆心距为6，那么这两圆的位置关系是 .‎ ‎（第16题）‎ ‎15. 在等腰梯形ABCD中，AD∥BC, AD＝‎3cm, AB＝‎4cm, ∠B＝60°, 则下底BC的长为 ‎ cm .‎ ‎16. 如图，⊙A和⊙B都与x轴和y轴相切，圆心A和圆心 B都在反比例函数的图象上，则图中阴影部分的 面积等于 . ‎ ‎17. 请你阅读下面的诗句:“栖树一群鸦，鸦树不知数，三 ‎ 只栖一树，五只没去处，五只栖一树，闲了一棵树，请你仔细数，鸦树各几何？” 诗句中谈到的鸦为 只、树为 棵.‎ ‎18.观察图中每一个大三角形中白色三角形的排列规律，则第5个大三角形中白色三角形 有 个 ．‎ ‎（第18题）‎ 三、解答题：‎ ‎19．（6分）‎ 计算：（π－1）°＋＋－2.‎ ‎20．（6分）‎ 解方程：.‎ ‎21．（8分）‎ 作为一项惠农强农应对当前国际金融危机、拉动国内消费需求的重要措施，“家电下乡”工作已经国务院批准从‎2008年12月1日起在我市实施．我市某家电公司营销点自去年12月份至今年5月份销售两种不同品牌冰箱的数量如下图： ‎ ‎（第21题）‎ ‎（1）完成下表：‎ 平均数 方差 甲品牌销售量/台 ‎10‎ 乙品牌销售量/台 ‎（2）请你依据折线图的变化趋势，对营销点今后的进货情况提出建议．‎ ‎22．（8分）‎ 坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋（公元1112年），为砖彻八角形十三层楼阁式建筑.数学活动小组开展课外实践活动，在一个阳光明媚的上午，他们去测量太子灵踪塔的高度，携带的测量工具有：测角仪、皮尺、小镜子.‎ ‎（1）小华利用测角仪和皮尺测量塔高. 图1为小华测量塔高的示意图.她先在塔前的平地上选择一点，用测角仪测出看塔顶的仰角，在点和塔之间选择一点，测出看塔顶的仰角，然后用皮尺量出、两点的距离为m,自身的高度为m.请你利用上述数据帮助小华计算出塔的高度（，结果保留整数）.‎ ‎（第22题）‎ 图1‎ 图2‎ ‎（2）如果你是活动小组的一员，正准备测量塔高，而此时塔影的长为m（如图2）,你能否利用这一数据设计一个测量方案？如果能，请回答下列问题： ‎ ‎①在你设计的测量方案中，选用的测量工具是: ； ‎ ‎②要计算出塔的高，你还需要测量哪些数据？ ‎ ‎ .‎ ‎23.（8分）‎ 阅读下面的材料：‎ ‎2‎ ‎4‎ ‎6‎ ‎2‎ ‎4‎ ‎6‎ ‎－2‎ ‎－2‎ ‎（第23题）‎ ‎ 在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数的图象为直线，一次函数的图象为直线，若，且，我们就称直线与直线互相平行. ‎ ‎ 解答下面的问题：‎ ‎ （1）求过点且与已知直线平行的直线的函数表达式,并画出直线 的图象；‎ ‎ （2）设直线分别与轴、轴交于点、，如果直线：与直线平行且交轴于点，求出△的面积关于的函数表达式.‎ ‎24.（9分） ‎ 如图，中，，，.半径为1的圆的圆心以1个单位/的速度由点沿方向在上移动，设移动时间为（单位：）.‎ ‎（1）当为何值时，⊙与相切；‎ ‎（2）作交于点，如果⊙和线段交于点，证明：当时，四边形为平行四边形.‎ ‎·‎ ‎（第24题）‎ 图1‎ 图2‎ ‎25.（9分）‎ 某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.‎ ‎（1）求商家降价前每星期的销售利润为多少元？‎ ‎（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？‎ ‎26. （12分）‎ 在平面直角坐标中，边长为2的正方形的两顶点、分别在轴、轴的正半轴上，点在原点.现将正方形绕点顺时针旋转，当点第一次落在直线上时停止旋转，旋转过程中，边交直线于点，边交轴于点（如图）.‎ ‎（1）求边在旋转过程中所扫过的面积；‎ ‎(第26题)‎ O A B C M N ‎（2）旋转过程中，当和平行时，求正方形 ‎ 旋转的度数；‎ ‎（3）设的周长为，在旋转正方形 的过程中，值是否有变化？请证明你的结论.‎ 数学试题参考答案及评分标准 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 选项 A C B C D D C D A C B C 二、填写题 ‎13. 14.外离 15.7 16.π 17. 20，5 18.121‎ 三、解答题 ‎19.解:原式＝1＋2＋（－5）－2………………………………………4分 ‎＝3＋3－5－2…………………………………5分 ‎＝－2. …………………………………6分 ‎20.解:方程两边同乘以（x-2），得 ……………………………………………1分 x-3+（x-2）=-3. ………………………………………………………3分 解得x=1. ……………….………………………………………………5分 检验：x=1时，x-2≠0，所以1是原分式方程的解. .……………………6分 ‎21.解：（1）计算平均数、方差如下表：‎ 平均数 方差 甲品牌销售量/台 ‎10‎ 乙品牌销售量/台 ‎10‎ ‎……………………………………………………6分 ‎（2）建议如下：从折线图来看，甲品牌冰箱的月销售量呈上升趋势，进货时可多进甲品牌冰箱． ………………………………………………8分 ‎22.解:（1）设的延长线交于点，长为，则.‎ ‎∵,∴.∴.‎ ‎∵,∴,解得.‎ ‎∴太子灵踪塔的高度为.………………………………4分 ‎(2) ①测角仪、皮尺； ② 站在P点看塔顶的仰角、自身的高度.‎ ‎(注：答案不唯一) ……………………………………8分 ‎23. 解：（1）设直线l的函数表达式为y＝k x＋b.‎ ‎∵ 直线l与直线y＝—2x—1平行，∴ k＝—2.‎ ‎∵ 直线l过点（1，4），∴ —2＋b ＝4，∴ b ＝6.‎ ‎ ∴ 直线l的函数表达式为y＝—2x＋6. ………………………3分 ‎2‎ ‎4‎ ‎6‎ ‎2‎ ‎4‎ ‎6‎ ‎－2‎ ‎－2‎ ‎（第23题）‎ 直线的图象如图. …………………………………………4分 ‎(2) ∵直线分别与轴、轴交于点、，∴点、的坐标分别为（0，6）、（3，0）.‎ ‎∵∥,∴直线为y＝—2x+t.‎ ‎∴C点的坐标为.‎ ‎∵ t＞0,∴ .‎ ‎∴C点在x轴的正半轴上.‎ 当C点在B点的左侧时，;‎ 当C点在B点的右侧时， .‎ ‎∴△的面积关于的函数表达式为 ‎…………………………8分 ‎24.(1)解：当⊙在移动中与相切时，设切点为，连，‎ 则.‎ ‎∴∽.∴.‎ ‎∵,,‎ ‎∴.∴.………………………………………………4分 ‎(2)证明：∵，，∴∥. ‎ 当时，.‎ ‎∴.∴.‎ ‎∴.‎ ‎∵∽,∴.∴，‎ ‎∴.∴.‎ ‎∴当时，四边形为平行四边形. ……………9分 ‎25．解：(1) （130-100）×80=2400（元）；…………………………………4分 ‎（2）设应将售价定为元，则销售利润 ‎……………………………………6分 ‎.……………………………………………8分 当时，有最大值2500.‎ ‎∴应将售价定为125元,最大销售利润是2500元. ……………9分 ‎26.（1）解：∵点第一次落在直线上时停止旋转，‎ ‎∴旋转了.‎ ‎∴在旋转过程中所扫过的面积为.……………4分 ‎（2）解：∵∥，‎ ‎∴,.‎ ‎∴.∴.‎ 又∵，∴.‎ 又∵,,∴.‎ ‎∴.∴.‎ ‎∴旋转过程中，当和平行时，正方形旋转的度数为 ‎.……………………………………………8分 ‎（3）答：值无变化.‎ ‎ 证明：延长交轴于点，则，‎ ‎，‎ ‎∴.‎ 又∵，.‎ ‎∴.‎ ‎∴. ‎ 又∵,,‎ ‎ ∴.∴.‎ ‎∴，‎ ‎∴.‎ ‎（第26题）‎ O A B C M N ‎∴在旋转正方形的过程中，值无变化. ……………12分