- 2021-05-13 发布 |
- 37.5 KB |
- 18页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学试卷分类汇编解直角三角形方位角问题
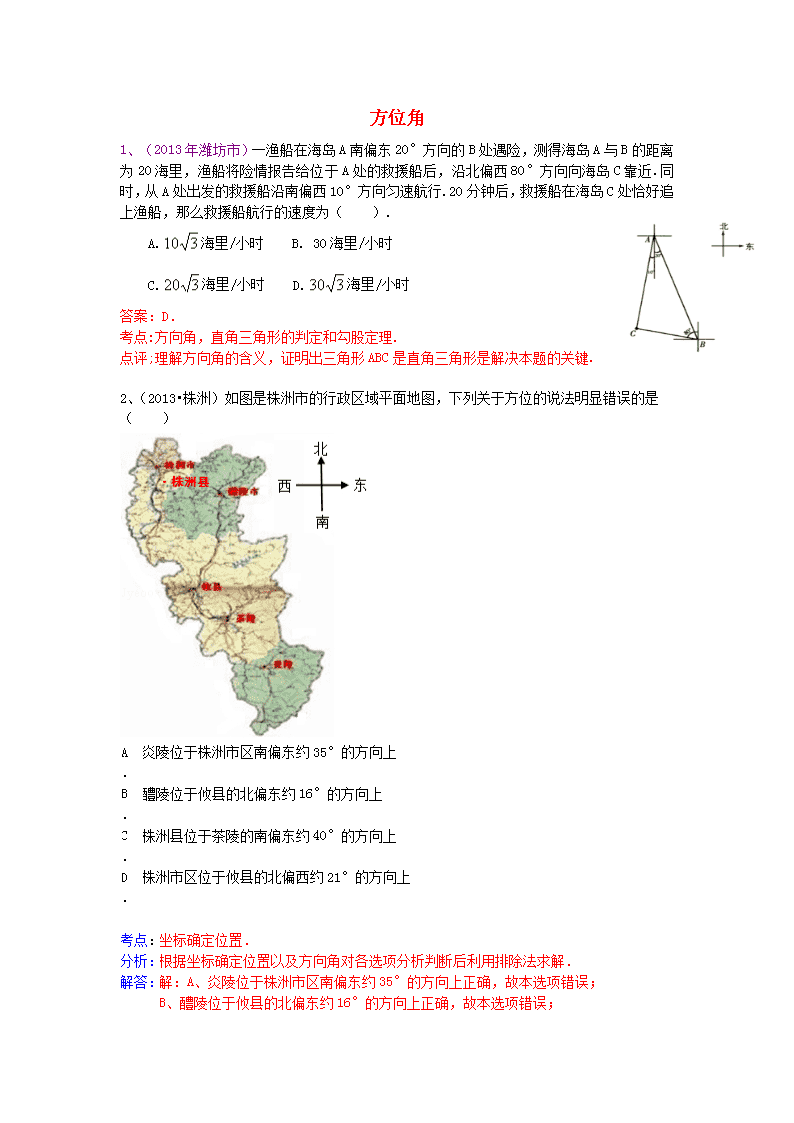
方位角 1、(2013年潍坊市)一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( ). A.海里/小时 B. 30海里/小时 C.海里/小时 D.海里/小时 答案:D. 考点:方向角,直角三角形的判定和勾股定理. 点评;理解方向角的含义,证明出三角形ABC是直角三角形是解决本题的关键. 2、(2013•株洲)如图是株洲市的行政区域平面地图,下列关于方位的说法明显错误的是( ) A. 炎陵位于株洲市区南偏东约35°的方向上 B. 醴陵位于攸县的北偏东约16°的方向上 C. 株洲县位于茶陵的南偏东约40°的方向上 D. 株洲市区位于攸县的北偏西约21°的方向上 考点: 坐标确定位置. 分析: 根据坐标确定位置以及方向角对各选项分析判断后利用排除法求解. 解答: 解:A、炎陵位于株洲市区南偏东约35°的方向上正确,故本选项错误; B、醴陵位于攸县的北偏东约16°的方向上正确,故本选项错误; C、应为株洲县位于茶陵的北偏西约40°的方向上,故本选项正确; D、株洲市区位于攸县的北偏西约21°的方向上正确,故本选项错误. 故选C. 点评: 本题考查了利用坐标确定位置,方向角的定义,是基础题,熟记方向角的概念并准确识图是解题的关键. 3、(2013年河北)如图1,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到 达位于灯塔P的北偏东40°的N处,则N处与灯塔P的 距离为 A.40海里 B.60海里 C.70海里 D.80海里 答案:D 解析:依题意,知MN=40×2=80,又∠M=70°,∠N=40°, 所以,∠MPN=70°,从而NP=NM=80,选D 4、(2013•荆门)A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由. 考点: 解直角三角形的应用-方向角问题. 分析: 首先过C作CD⊥AB与D,由题意得:∠ACD=α,∠BCD=β,即可得在Rt△ACD中,AD=CD•tanα,在Rt△BCD中,BD=CD•tanβ,继而可得CD•tanα+CD•tanβ=AB,则可求得CD的长,即可知连接AB高速公路是否穿过风景区. 解答: 解:AB不穿过风景区.理由如下: 如图,过C作CD⊥AB于点D, 根据题意得:∠ACD=α,∠BCD=β, 则在Rt△ACD中,AD=CD•tanα,在Rt△BCD中,BD=CD•tanβ, ∵AD+DB=AB, ∴CD•tanα+CD•tanβ=AB, ∴CD==(千米). ∵CD=50>45, ∴高速公路AB不穿过风景区. 点评: 此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键. 5、(2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短. (1)请在图中作出该船在点B处的位置; (2)求钓鱼岛C到B处距离(结果保留根号) 考点: 解直角三角形的应用-方向角问题. 分析: (1)根据垂线段最短知B点应是过C点所作南北方向的垂线的垂足. (2)在Rt△ABC中,利用三角函数的知识求BC即可. 解答: 解:(1)如图: (2)在Rt△ABC中 ∵AB=30×0.5=15(海里), ∴BC=ABtan30°=15×=5(海里). 答:钓鱼岛C到B处距离为5海里. 点评: 考查了解直角三角形的应用﹣方向角问题,此题为基础题,涉及用手中工具解题,如尺规,计算器等. 6、(2013年广州市)如图10, 在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里. (1) 求船P到海岸线MN的距离(精确到0.1海里); (2) 若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处. 分析:(1)过点P作PE⊥AB于点E,在Rt△APE中解出PE即可; (2)在Rt△BPF中,求出BP,分别计算出两艘船需要的时间,即可作出判断 解:(1)过点P作PE⊥AB于点E, 由题意得,∠PAE=32°,AP=30海里, 在Rt△APE中,PE=APsin∠PAE=APsin32°≈15.9海里; (2)在Rt△PBE中,PE=15.9海里,∠PBE=55°, 则BP=≈19.4, A船需要的时间为:=1.5小时,B船需要的时间为:=1.3小时, 故B船先到达. 点评:本题考查了解直角三角形的应用,解答本题的关键是理解方位角的定义,能利用三角函数值计算有关线段,难度一般. 7、(2013年广东湛江)如图,我国渔政船在钓鱼岛海域处测得钓鱼岛在渔政船的北 偏西的方向上,随后渔政船以80海里小时的速度向北偏东 的方向航行,半小时后到达处,此时又测得钓鱼岛在渔政船 的北偏西的方向上,求此时渔政船距钓鱼岛的距离. (结果保留小数点后一位,) 解:延长至,则, , 在△中,,, 答:此时渔政船距钓鱼岛的距离约为:海里 8、(2013•荆门)A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由. 考点: 解直角三角形的应用-方向角问题. 分析: 首先过C作CD⊥AB与D,由题意得:∠ACD=α,∠BCD=β,即可得在Rt△ACD中,AD=CD•tanα,在Rt△BCD中,BD=CD•tanβ,继而可得CD•tanα+CD•tanβ=AB,则可求得CD的长,即可知连接AB高速公路是否穿过风景区. 解答: 解:AB不穿过风景区.理由如下: 如图,过C作CD⊥AB于点D, 根据题意得:∠ACD=α,∠BCD=β, 则在Rt△ACD中,AD=CD•tanα,在Rt△BCD中,BD=CD•tanβ, ∵AD+DB=AB, ∴CD•tanα+CD•tanβ=AB, ∴CD==(千米). ∵CD=50>45, ∴高速公路AB不穿过风景区. 点评: 此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键. 9、(2013•苏州)如图,在一笔直的海岸线l上有AB两个观测站,A在B的正东方向,AB=2(单位:km).有一艘小船在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向. (1)求点P到海岸线l的距离; (2)小船从点P处沿射线AP的方向航行一段时间后,到点C处,此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述两小题的结果都保留根号) 考点: 解直角三角形的应用-方向角问题. 分析: (1)过点P作PD⊥AB于点D,设PD=xkm,先解Rt△PBD,用含x的代数式表示BD,再解Rt△PAD,用含x的代数式表示AD,然后根据BD+AD=AB,列出关于x的方程,解方程即可; (2)过点B作BF⊥AC于点F,先解Rt△ABF,得出BF=AB=1km,再解Rt△BCF,得出BC=BF=km. 解答: 解:(1)如图,过点P作PD⊥AB于点D.设PD=xkm. 在Rt△PBD中,∠BDP=90°,∠PBD=90°﹣45°=45°, ∴BD=PD=xkm. 在Rt△PAD中,∠ADP=90°,∠PAD=90°﹣60°=30°, ∴AD=PD=xkm. ∵BD+AD=AB, ∴x+x=2, x=﹣1, ∴点P到海岸线l的距离为(﹣1)km; (2)如图,过点B作BF⊥AC于点F. 在Rt△ABF中,∠AFB=90°,∠BAF=30°, ∴BF=AB=1km. 在△ABC中,∠C=180°﹣∠BAC﹣∠ABC=45°. 在Rt△BCF中,∠BFC=90°,∠C=45°, ∴BC=BF=km, ∴点C与点B之间的距离为km. 点评: 本题考查了解直角三角形的应用﹣方向角问题,难度适中.通过作辅助线,构造直角三角形是解题的关键. 10、(2013•莱芜)如图,有一艘渔船在捕鱼作业时出现故障,急需抢修,调度中心通知附近两个小岛A、B上的观测点进行观测,从A岛测得渔船在南偏东37°方向C处,B岛在南偏东66°方向,从B岛测得渔船在正西方向,已知两个小岛间的距离是72海里,A岛上维修船的速度为每小时20海里,B岛上维修船的速度为每小时28.8海里,为及时赶到维修,问调度中心应该派遣哪个岛上的维修船? (参考数据:cos37°≈0.8,sin37°≈0.6,sin66°≈0.9,cos66°≈0.4) 考点: 解直角三角形的应用-方向角问题. 分析: 作AD⊥BC的延长线于点D,先解Rt△ADB,求出AD,BD,再解Rt△ADC,求出AC,CD,则BC=BD﹣CD.然后分别求出A岛、B岛上维修船需要的时间,则派遣用时较少的岛上的维修船. 解答: 解:作AD⊥BC的延长线于点D. 在Rt△ADB中,AD=AB•cos∠BAD=72×cos66°=72×0.4=28.8(海里), BD=AB•sin∠BAD=72×sin66°=72×0.9=64.8(海里). 在Rt△ADC中,(海里), CD=AC•sin∠CAD=36×sin37°=36×0.6=21.6(海里). BC=BD﹣CD=64.8﹣21.6=43.2(海里). A岛上维修船需要时间(小时). B岛上维修船需要时间(小时). ∵tA<tB, ∴调度中心应该派遣B岛上的维修船. 点评: 本题考查了解直角三角形的应用﹣方向角问题,难度适中,通过作辅助线,构造直角三角形,进而解直角三角形求出BD与CD的值是解题的关键. 11、(2013泰安)如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为 (取,结果精确到0.1海里). 考点:解直角三角形的应用-方向角问题. 专题:应用题. 分析:过点D作DE⊥AB于点E,设DE=x,在Rt△CDE中表示出CE,在Rt△BDE中表示出BE,再由CB=25海里,可得出关于x的方程,解出后即可计算AB的长度. 解答:解:∵∠DBA=∠DAB=45°, ∴△DAB是等腰直角三角形, 过点D作DE⊥AB于点E,则DE=AB, 设DE=x,则AB=2x, 在Rt△CDE中,∠DCE=30°, 则CE=DE=x, 在Rt△BDE中,∠DAE=45°, 则DE=BE=x, 由题意得,CB=CE﹣BE=x﹣x=25, 解得:x=, 故AB=25(+1)=67.5海里. 故答案为:67.5. 点评:本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度,难度一般. 12、(2013•烟台)如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里.求A、C两地之间的距离(参考数据:≈1.41,≈1.73,≈2.45,结果精确到0.1) 考点: 解直角三角形的应用-方向角问题. 分析: 过点B作BD⊥CA交CA延长线于点D,根据题意可得∠ACB和∠ABC的度数,然后根据三角形外角定理求出∠DAB的度数,已知AB=12海里,可求出BD、AD的长度,在Rt△CBD中,解直角三角形求出CD的长度,继而可求出A、C之间的距离. 解答: 解:过点B作BD⊥CA交CA延长线于点D, 由题意得,∠ACB=60°﹣30°=30°, ∠ABC=75°﹣60°=15°, ∴∠DAB=∠DBA=45°, 在Rt△ABD中,AB=12,∠DAB=45°, ∴BD=AD=ABcos45°=6, 在Rt△CBD中,CD==6, ∴AC=6﹣6≈6.2(海里). 答:A、C两地之间的距离为6.2海里. 点评: 本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度,难度一般. 13、(2013•遂宁)钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛 海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号) 考点: 解直角三角形的应用-方向角问题. 分析: 首先过点B作BD⊥AC于D,由题意可知,∠BAC=45°,∠ABC=90°+15°=105°,则可求得∠ACD的度数,然后利用三角函数的知识求解即可求得答案. 解答: 解:过点B作BD⊥AC于D. 由题意可知,∠BAC=45°,∠ABC=90°+15°=105°, ∴∠ACB=180°﹣∠BAC﹣∠ABC=30°, 在Rt△ABD中,BD=AB•sin∠BAD=20×=10(海里), 在Rt△BCD中,BC===20(海里). 答:此时船C与船B的距离是20海里. 点评: 此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键. 14、(2013•资阳)钓鱼岛历来是中国领土,以它为圆心在周围12海里范围内均属于禁区,不允许它国船只进入,如图,今有一中国海监船在位于钓鱼岛A正南方距岛60海里的B处海域巡逻,值班人员发现在钓鱼岛的正西方向52海里的C处有一艘日本渔船,正以9节的速度沿正东方向驶向钓鱼岛,中方立即向日本渔船发出警告,并沿北偏西30°的方向以12节的速度前往拦截,期间多次发出警告,2小时候海监船到达D处,与此同时日本渔船到达E处,此时海监船再次发出严重警告. (1)当日本渔船受到严重警告信号后,必须沿北偏东转向多少度航行,才能恰好避免进入钓鱼岛12海里禁区? (2)当日本渔船不听严重警告信号,仍按原速度,原方向继续前进,那么海监船必须尽快到达距岛12海里,且位于线段AC上的F处强制拦截渔船,问海监船能否比日本渔船先到达F处?(注:①中国海监船的最大航速为18节,1节=1海里/小时;②参考数据:sin26.3°≈0.44,sin20.5°≈0.35,sin18.1°≈0.31,≈1.4,≈1.7) 考点: 解直角三角形的应用-方向角问题 分析: (1)过点E作圆A的切线EN,求出∠AEN的度数即可得出答案; (2)分别求出渔船、海监船到达点F的时间,然后比较可作出判断. 解答: 解:(1)过点E作圆A的切线EN,连接AN,则AN⊥EN, 由题意得,CE=9×2=18海里,则AE=AC﹣CE=52﹣18=34海里, ∵sin∠AEN==≈0.35, ∴∠AEN=20.5°, ∴∠NEM=69.5°, 即必须沿北偏东至少转向69.5°航行,才能恰好避免进入钓鱼岛12海里禁区. (2)过点D作DH⊥AB于点H, 由题意得,BD=2×12=24海里, 在Rt△DBH中,DH=BD=12海里,BH=12海里, ∵AF=12海里, ∴DH=AF, ∴DF⊥AF, 此时海监船以最大航速行驶, 海监船到达点F的时间为:==≈2.2小时; 渔船到达点F的时间为:==2.4小时, ∵2.2<2.4, ∴海监船比日本渔船先到达F处. 点评: 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,本题依托时事问题出题,立意新颖,是一道很好的题目. 15、(2013•自贡)在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处. (1)求该轮船航行的速度(保留精确结果); (2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由. 考点: 解直角三角形的应用-方向角问题. 分析: (1)根据∠1=30°,∠2=60°,可知△ABC为直角三角形.根据勾股定理解答. (2)延长BC交l于T,比较AT与AM、AN的大小即可得出结论. 解答: 解:(1)∵∠1=30°,∠2=60°, ∴△ABC为直角三角形. ∵AB=40km,AC=km, ∴BC===16(km). ∵1小时20分钟=80分钟,1小时=60分钟, ∴×60=12(千米/小时). (2)作线段BR⊥x轴于R,作线段CS⊥x轴于S,延长BC交l于T. ∵∠2=60°, ∴∠4=90°﹣60°=30°. ∵AC=8(km), ∴CS=8sin30°=4(km). ∴AS=8cos30°=8×=12(km). 又∵∠1=30°, ∴∠3=90°﹣30°=60°. ∵AB=40km, ∴BR=40•sin60°=20(km). ∴AR=40×cos60°=40×=20(km). 易得,△STC∽△RTB, 所以=, , 解得:ST=8(km). 所以AT=12+8=20(km). 又因为AM=19.5km,MN长为1km,∴AN=20.5km, ∵19.5<AT<20.5 故轮船能够正好行至码头MN靠岸. 点评: 此题结合方向角,考查了阅读理解能力、解直角三角形的能力.计算出相关特殊角和作出辅助线构造相似三角形是解题的关键. 16、(2013年黄石)高考英语听力测试期间,需要杜绝考点周围的噪音。如图,点是某市一高考考点,在位于考点南偏西15°方向距离125米的点处有一消防队。在听力考试期间,消防队突然接到报警电话,告知在位于点北偏东75°方向的点处突发火灾,消防队必须立即赶往救火。已知消防车的警报声传播半径为100米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶。试问: C 北 A 15° 75° F 北 消防车是否需要改道行驶?说明理由.(取1.732) 解析: 解:过点作交于点,由图可知 ∵ (3分) ∴ (3分) ∵米 ∴不需要改道行驶 17、(2013四川南充,21,8分)如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据:sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75). (1)求M,N两村之间的距离; (2)要在公路AB旁修建一个土特产收购站P,使得M,N两村到P站的距离之和最短,求这个最短距离。 北A A N M B 解析: (1)如图,过点M作CD∥AB,NE⊥AB. ……………1′ 在Rt△ACM中,∠CAM=36.5°,AM=5, ∴sin36.5°= =0.6, ∴CM=3,AC=4. ……………2′ 在Rt△ANE中, ∠NAE=90°-53.5°=36.5°,AN=10, ∴sin36.5°= =0.6 ∴NE=6,AE=8. ……………3′ 在Rt△MND中,MD=5,ND=2. ∴MN= = (km) ……………4′ (2)作点N关于AB的对称点G,连接MG交AB于点P. 点P即为站点. ……………5′ ∴PM+PN=PM+PG=MG. ……………6′ 在Rt△MDG中,MG===(km) ……………7′ ∴最短距离为 km ……………8′ P 北A A N M B C D G E 18、(2013•新疆)如图所示,一条自西向东的观光大道l上有A、B两个景点,A、B相距2km,在A处测得另一景点C位于点A的北偏东60°方向,在B处测得景点C位于景点B的北偏东45°方向,求景点C到观光大道l的距离.(结果精确到0.1km) 考点: 解直角三角形的应用-方向角问题. 分析: 过点C作CD⊥l于点D,设CD=xkm.先解直角△ACD,得出AD=CD=xkm,再解直角△BCD,得出BD=CD=xkm,然后根据AD﹣BD=AB,列出关于x的方程,解方程即可. 解答: 解:如图,过点C作CD⊥l于点D,设CD=xkm. 在△ACD中,∵∠ADC=90°,∠CAD=30°, ∴AD=CD=xkm. 在△BCD中,∵∠BDC=90°,∠CBD=45°, ∴BD=CD=xkm. ∵AD﹣BD=AB, ∴x﹣x=2, ∴x=+1≈2.7(km). 故景点C到观光大道l的距离约为2.7km. 点评: 本题考查三角形知识的实际运用,难度适中,通过作辅助线构造直角三角形是解题的关键. 19、(2013济宁)钓鱼岛及其附属岛屿是中国固有领土(如图1),A、B、C分别是钓鱼岛、南小岛、黄尾屿上的点(如图2),点C在点A的北偏东47°方向,点B在点A的南偏东79°方向,且A、B两点的距离约为5.5km;同时,点B在点C的南偏西36°方向.若一艘中国渔船以30km/h的速度从点A驶向点C捕鱼,需要多长时间到达(结果保留小数点后两位)?(参考数据:sin54°≈0.81,cos54°≈0.59,tan47°≈1.07,tan36°≈0.73,tan11°≈0.19) 考点:解直角三角形的应用-方向角问题. 分析:过点B作BD⊥AC交AC于点D,根据方向角分别求出∠DAB和∠DCB的度数,然后在Rt△ABD和Rt△BCD中,分别解直角三角形求出AD、CD的长度,然后根据时间=路程÷速度即可求出需要的时间. 解答:解:过点B作BD⊥AC交AC于点D, 由题意得,∠DAB=180°﹣47°﹣79°=54°, ∠DCB=47°﹣36°=11°, 在Rt△ABD中, ∵AB=5.5,∠DAB=54°, =cos54°,=sin54°, ∴AD=5.5×0.59=3.245,BD=4.445, 在Rt△BCD中, ∵BD=4.445,∠DCB=11°, ∴=tan11°, ∴CD==23.394, ∴AC=AD+CD=3.245+23.394≈26.64(km), 则时间t=26.64÷30≈0.90(h). 答:需要0.90h到达. 点评:本题考查了解直角三角形的应用,难度适中,解答本题的关键是构造直角三角形并解直角三角形, 20、(2013达州) 钓鱼岛自古以来就是中国领土。中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测。如图,E、F为钓鱼岛东西两端。某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=公里,在A点测得钓鱼岛最西端F在最东端E的东北方向(C、F、E在同一直线上)。求钓鱼岛东西两端的距离。(,,结果精确到0.1) 解析: 由题知,在Rt△ACF中,∠ACF=90°, ∠A=30°,CF=20公里. ∴cot30°=. 解得,AC=60(公里).………………………(2分) 又∵E在B的东北方向,且∠ACF=90° ∴∠E=∠CBE=45°, ∴CE=CB.………………………………………………(4分) 又∵CB=AC-AB=60-22=38(公里), ∴CE=38公里.………………………(5分) ∴EF=CE-CF=38-20≈3.4(公里)………………………(6分) 答:钓鱼岛东西两端的距离约为3.4公里.………………………(7分) 结束查看更多