- 2021-05-13 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
南充市中考数学试题
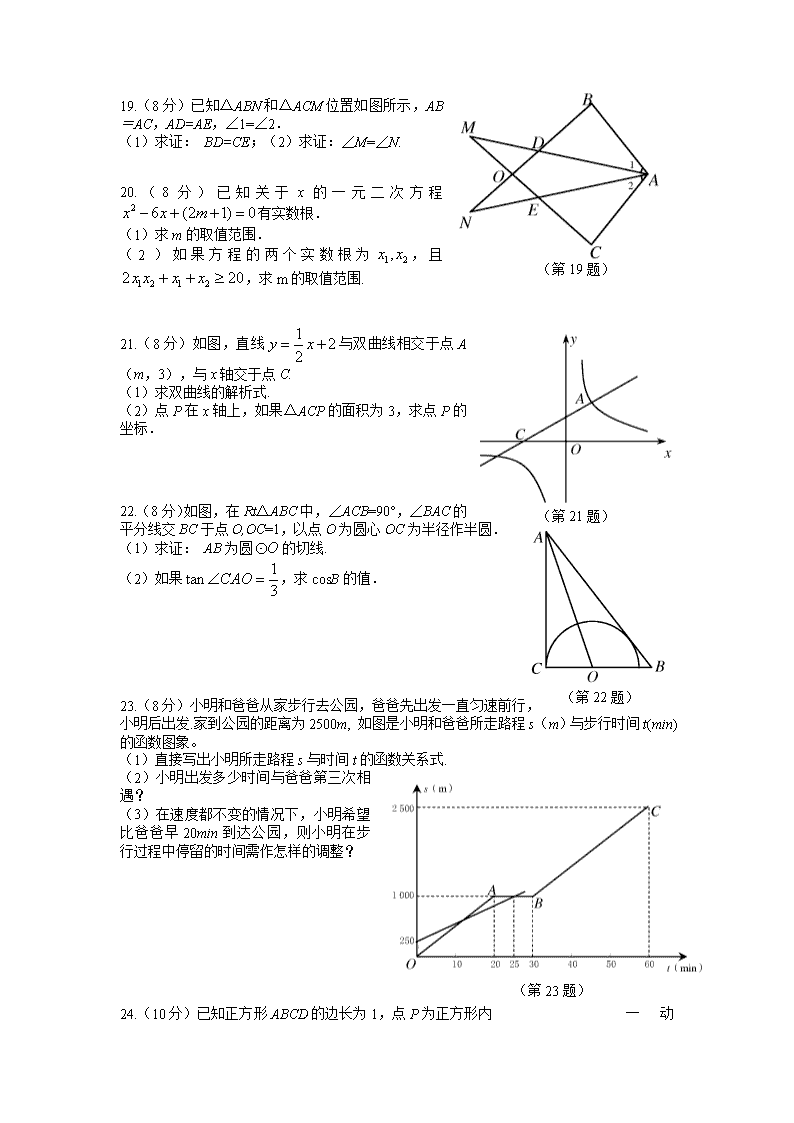
南充市二〇一六年高中阶段教育学校招生考试 数 学 试 题 (满分120分,时间120分钟) 一、选择题(本大题共10个小题,每小题3分,共30分) 每小题都有代号为A、B、C、D四个答案选项,其中只有一个是正确的.请根据正确选项代号在答题卡对应位置填涂.填涂正确记3分,不涂、错涂或多涂记0分. 1. 如果向右走5步记为+5,那么向左走3步记为( ) (A)+3 (B)-3 (C) (D) 2. 下列计算正确的是( ) (A) (B) (C) (D) 3. 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( ) (A)AM=BM (B)AP=BN (C)∠MAP=∠MBP (D)∠ANM=∠BNM M P A B N (第3题) (第4题) 4. 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是( ) (A)12岁 (B)13岁 (C)14岁 (D)15岁 5. 抛物线的对称轴是( ) (A)直线 (B)直线 (C)直线 (D)直线 6.某次列车平均提速20km/h,用相同的时间,列车提速前行驶400km,提速后比提速前多行驶100km.设提速前列车的平均速度为xkm/h,下列方程正确的是( ) (A) (B) (C) (D) 7.如图,在Rt△ABC中,∠A=30°,BC=1,点D、E分别是直角边BC、AC的中点,则DE的长为( ) (A)1 (B)2 (C) (D) 8.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落在EF上点G处,并使折痕经过点A,展开纸片后∠DAG的大小为( ) (A)30° (B)45° (C)60° (D)75° 9.不等式的正整数解的个数是( ) (A)1个 (B)2个 (C)3个 (D)4个 A D C E B D C E F A B G E A D B C M N (第7题) (第8题) (第10题) 10.如图,正五边形的边长为2,连接对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N.给出下列结论:①∠AME=108°;②;③;④.其中正确结论的个数是( ) (A)1个 (B)2个 (C)3个 (D)4个[ 二、填空题(本大题共6个小题,每小题3分,共18分) 请将答案直接填写在对应横线上. 11. 计算= . 12. 如图,菱形的周长是8cm,则AB的长是 cm. 13. 计算22,24,26,28,30这组数据的方差是 . 14. 如果,且,则n的值是 . 15. 如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm. (第12题) (第15题) 16.已知抛物线开口向上且经过点(1,1),双曲线经过点()给出下列结论:①;②;③是关于x的一元二次方程的两个实数根;④.其中正确结论是 (填写序号). 三、解答题(本大题共9个小题,共72分) 解答应写出必要的文字说明,证明过程或演算步骤. 17.(6分) 计算:. 18.(6分)在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖. (1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率.(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率. 19.(8分)已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2. (1)求证: BD=CE;(2)求证:∠M=∠N. 20.(8分)已知关于x的一元二次方程有实数根. (1)求m的取值范围. (第19题) (2)如果方程的两个实数根为,且,求m的取值范围. 21.(8分)如图,直线与双曲线相交于点A(m,3),与x轴交于点C. (1)求双曲线的解析式. (2)点P在x轴上,如果△ACP的面积为3,求点P的坐标. (第21题) 22.(8分)如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线交BC于点O,OC=1,以点O为圆心OC为半径作半圆. (1)求证: AB为圆的切线. (2)如果,求cosB的值. (第22题) 23.(8分)小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m, 如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象。 (1)直接写出小明所走路程s与时间t的函数关系式. (2)小明出发多少时间与爸爸第三次相遇? (3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整? (第23题) 24.(10分)已知正方形ABCD的边长为1,点P 为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连接CM. (1)如图一,若点M在线段AB上,求证: AP⊥BN; AM=AN. (2)①如图二,在点P运动过程中,满足△PBC∽△PAM的点M在AB的延长线上时,AP⊥BN和AM=AN是否成立(不需说明理由)? ②是否存在满足条件的点P,使得PC=? 请说明理由. (第24题) 25.(10分)如图,抛物线与x轴交于点A(-5,0)和B(3,0),与y轴相交于点C(0,5).有一宽度为1,长度足够的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和Q, 交直线AC于点M和N,交x轴于点E和F. (1)求抛物线解析式. (2)当点M和N都在线段AC上时,连接MF,如果,求点Q的坐标. (3)在矩形的平移过程中,当以点P, Q ,M, N为顶点的四边形是平行四边形时,求点M的坐标. (第25题)查看更多