上海市徐汇区中考二模数学试题及答案

上海市徐汇区中考二模数学试题及答案

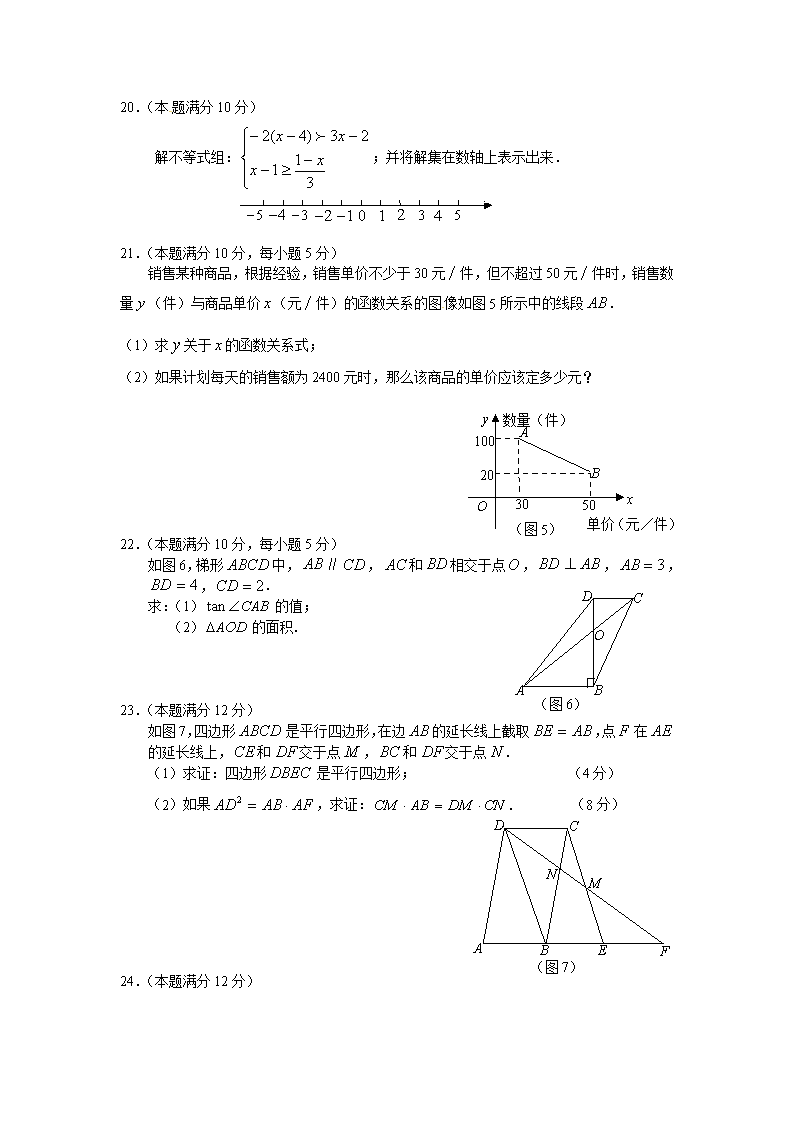
‎2013学年第二学期徐汇区学习能力诊断卷 初三年级数学学科 ‎ 2013.4‎ ‎（时间100分钟 满分150分） ‎ 考生注意∶‎ ‎1．本试卷含三个大题，共25题；答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效；‎ ‎2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．‎ 一．选择题（本大题共6题，每题4分，满分24分）‎ ‎1．下列二次根式中与是同类二次根式的是 Ａ．； Ｂ．； Ｃ．； Ｄ．． ‎ ‎2．将抛物线向下平移2个单位后，所得抛物线解析式为 Ａ．； Ｂ．；Ｃ．； Ｄ．．‎ ‎3．如果关于的一元二次方程有两个不相等的实数根，那么的取值范围是 Ａ．＞； Ｂ．＜； Ｃ．＞且；Ｄ．＜且．‎ ‎4．下列一组数据：、、、、的平均数和方差分别是 Ａ．和； Ｂ．和； Ｃ．和； Ｄ．和． ‎ ‎5．下列正方形的性质中，菱形（非正方形）不具有的性质是 ‎ Ａ．四边相等； Ｂ．对角线相等；‎ Ｃ．对角线平分一组对角； Ｄ．对角线互相平分且垂直．‎ ‎6．在中，，，那么半径长为的⊙和直线的位置关系是 Ａ．相离； Ｂ．相切； Ｃ．相交； Ｄ．无法确定． ‎ 二．填空题（本大题共12题，每题4分，满分48分）‎ ‎7．化简： ▲ ．‎ ‎8．计算：_______▲_________．‎ ‎9．方程的解是 ▲ ． ‎ ‎10．已知函数，那么 ▲ .‎ ‎11．如图1，点在反比例函数的图像上，那么该反比例函数的解析式是 ▲ ．‎ ‎12．如图2，在中，中线和相交于点，如果，=，那么向量▲ ．‎ ‎13．如图3，∥，平分，如果，那么 ▲ ．‎ ‎14．在形状、大小、颜色都一样的卡片上，分别画有线段、直角三角形、等腰三角形、等边三角形、平行四边形、菱形、等腰梯形、正五边形、正六边形、圆等10个图形，小杰随机抽取一张卡片，抽得图形既是轴对称图形，又是中心对称图形的概率是___▲_____． ‎ ‎15．为了解某校初三年级学生一次数学测试成绩的情况，从近450名九年级学生中，随机抽取50名学生这次数学测试的成绩，通过数据整理，绘制如下统计表（给出部分数据，除[90,100]组外每组数据含最低值，不含最高值）： ‎ 分数段 ‎[ 0, 60]‎ ‎[60, 70]‎ ‎[70, 80]‎ ‎[80, 90]‎ ‎[90,100]‎ 频 数 ‎5‎ ‎20‎ 频 率 ‎0.12‎ ‎0.1‎ 根据上表的信息，估计该校初三年级本次数学测试的优良率（80分及80分以上）约为▲ （填百分数）．‎ ‎16．如图4，⊙半径为，的顶点在⊙上，，，垂足是，，那么的长为 ▲ ．‎ ‎17．一个二元一次方程和一个二元二次方程组成的二元二次方程组的解是或，试写出一个符合要求的方程组__________▲ _____________（只需写一个）．‎ A B C D ‎（图3）‎ ‎（图1）‎ x O y A ‎3‎ ‎1‎ A B C D E G ‎（图2）‎ ‎（图4）‎ A B C D O ‎18．在中，，，将绕点旋转后，点落在射线上，点落到点处，那么的值等于 ▲ ．‎ 三．（本大题共7题，第19—22题每题10分；第23、24题每题12分；第25题14分；‎ 满分78分）‎ ‎19．（本题满分10分）‎ ‎ 计算：．‎ ‎20．（本题满分10分）‎ 解不等式组：；并将解集在数轴上表示出来．‎ x ‎21．（本题满分10分，每小题5分）‎ 销售某种商品，根据经验，销售单价不少于30元∕件，但不超过50元∕件时，销售数 量（件）与商品单价（元∕件）的函数关系的图像如图5所示中的线段.‎ ‎（1）求关于的函数关系式；‎ ‎（2）如果计划每天的销售额为2400元时，那么该商品的单价应该定多少元？‎ 数量（件）‎ ‎（图5）‎ x O y ‎100‎ ‎20‎ ‎30‎ ‎50‎ 单价（元／件）‎ A B ‎22．（本题满分10分，每小题5分）‎ ‎（图6）‎ A B C D O 如图6，梯形中，∥，和相交于点，，，，.‎ 求：（1）的值； ‎ ‎（2）的面积. ‎ ‎23．（本题满分12分）‎ 如图7，四边形是平行四边形，在边的延长线上截取，点在的延长线上，和交于点，和交于点.‎ ‎（1）求证：四边形是平行四边形； （4分）‎ A B C D E F M ‎（图7）‎ N ‎（2）如果，求证：. （8分）‎ ‎24．（本题满分12分）‎ 抛物线（）经过点，对称轴是直线，顶点是，与 轴正半轴的交点为点． ‎ ‎（1）求抛物线（）的解析式和顶点的坐标； （6分）‎ ‎（2）过点作轴的垂线交轴于点，点在射线上，当以为直径的⊙和 以为半径的⊙相切时，求点的坐标． （6分）[‎ ‎25．（本题满分14分）‎ 如图8，在中，，，，点是边上任意一点，过点作交于点，截取，联结，线段交于点，设，．‎ ‎（1）求关于的函数解析式及定义域； （4分）‎ ‎（2）如图9，联结，当和相似时，求的值； （5分）‎ ‎（图8）‎ C A B D E P Q C A B D E P Q ‎（图9）‎ ‎（备用图）‎ C A B ‎（3）当以点为圆心，为半径的⊙和以点为圆心，为半径的⊙相交的另一个交点在边上时，求的长． （5分）‎ ‎2012学年第二学期徐汇区学习能力诊断卷 初三年级数学学科参考答案和评分标准 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．C； 2．D； 3．B； 4．A； 5．B； 6．B．‎ 二．填空题：（本大题共12题，满分48分）‎ ‎7．； 8．； 9．或； 10．； 11．； 12．；‎ ‎13．；14．；15．﹪；16．；17．不唯一，如等； 18．或．‎ 三、（本大题共7题，第19、20、21、22题每题10分，第23、24题每题12分，第25题14分，满分78分）‎ ‎19. 解：原式 …………………………………………………（8分）‎ ‎ ……………………………………………………………………（2分）‎ ‎20．解：由不等式（1）解得＜………………………………………………………（3分）‎ 由不等式（2）解得≥…………………………………………………………（3分）‎ ‎∴原不等式组的解集是≤＜ ……………………………………………（2分）‎ 图正确．……………………………………………………………………………（2分）‎ ‎21．解：（1）设关于的函数关系式为．…………………………（1分）‎ ‎ 由题意，得 ……………………………………………（2分）‎ 解得，……………………………………………………………（1分）‎ ‎∴ 关于的函数关系式为． …………………………（1分）‎ ‎（2）设该商品的单价应该定元．………………………………………………（1分）‎ 由题意，得…………………………………………（1分）‎ 化简整理，得．………………………………………（1分）‎ 解得，，． ………………………………………………（1分）‎ ‎ 经检验，不合题意，舍去；………………………………………（1分）‎ 答：计划每天的销售额为2400元时，该商品的单价应该定元． ‎ ‎22．解：（1）∵∥，∴． ……………………………………（2分）‎ ‎∵，∴．………………………………………（1分）‎ 在中，， ‎ ‎∴．…………………………………………………（2分）‎ ‎（2）∵ …………………………………………（2分）‎ ‎∴．…………………………………（3分）23．证明：（1） ∵四边形是平行四边形，‎ ‎∴∥，；…………………………………………（2分）‎ ‎∵，∴；…………………………………………（1分）‎ 又∥，‎ ‎∴四边形是平行四边形．………………………………………（1分）‎ ‎（2） ∵，∴，………………………………（1分）‎ 又，∴∽，∴； ……（1分）‎ ‎∵∥，∴；………………………………（1分）‎ ‎∵四边形是平行四边形，∴∥，∴；（1分）‎ ‎∵四边形是平行四边形，∴∥，∴；（1分）‎ ‎∴；…………………………………………………（1分）‎ 又，∴∽，∴，…（1分）‎ ‎∵，∴，‎ ‎∴．………………………………………………（1分）‎ ‎24．解：（1）由题意，得，…………………………………………………（2分）‎ 解得 ……………………………………………………………（2分）‎ ‎∴ ………………………………………………………（1分）‎ ‎∴顶点． …………………………………………………………（1分）‎ ‎（2）设⊙的半径为．‎ 由题意，可得，，∴⊙的半径为；；……（2分）‎ 当⊙和⊙相切时，分下列两种情况：‎ ‎ 当⊙和⊙外切时，此时点在线段上，‎ 可得．‎ 解得，∴．……………………………………………（2分）‎ ‎ 当⊙和⊙外切时，此时点在线段的延长线上，‎ 可得．‎ 解得，∴．…………………………………………（2分）‎ 综合，当⊙和⊙相切时，或．‎ ‎25．解：（1）过点作，垂足为．‎ 由题意，可知是等腰直角三角形，∴；……………（1分）‎ 易得∽，∴；‎ 设，，∴，∴，‎ ‎∴……………………………………………………………（1分）‎ ‎∴．………………………………………………………（1分）‎ 定义域是：≤≤ ．………………………………………………（1分）‎ ‎（注：其它解法参照评分．）‎ ‎（2）∵，∴当和相似时，分以下两种情况：（1分）‎ ‎ 当时，∴∥，易得四边形是正方形；‎ ‎ ∴． …………………………………………………（2分）‎ ‎ 当时，∴，‎ ‎ 由上述（1）的解法，可得，‎ ‎∴，∴；‎ ‎∴，解得．………………………………（2分）‎ ‎ 综合，当和相似时，的值为或．‎ ‎（3）如图，设⊙与⊙相交的另一个交点为，联结交于点．‎ ‎ ∴,.易得∽，∽，‎ ‎∴，设，，∴； …（1分）‎ ‎ ∴，∴；∵，∴； …（1分）‎ ‎ 又，∴，解得； ……………（2分）‎ P C A B M N Q ‎ ∴．…………………………………………………（1分）‎