- 2021-05-11 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
03中考模拟数学试题三及答案
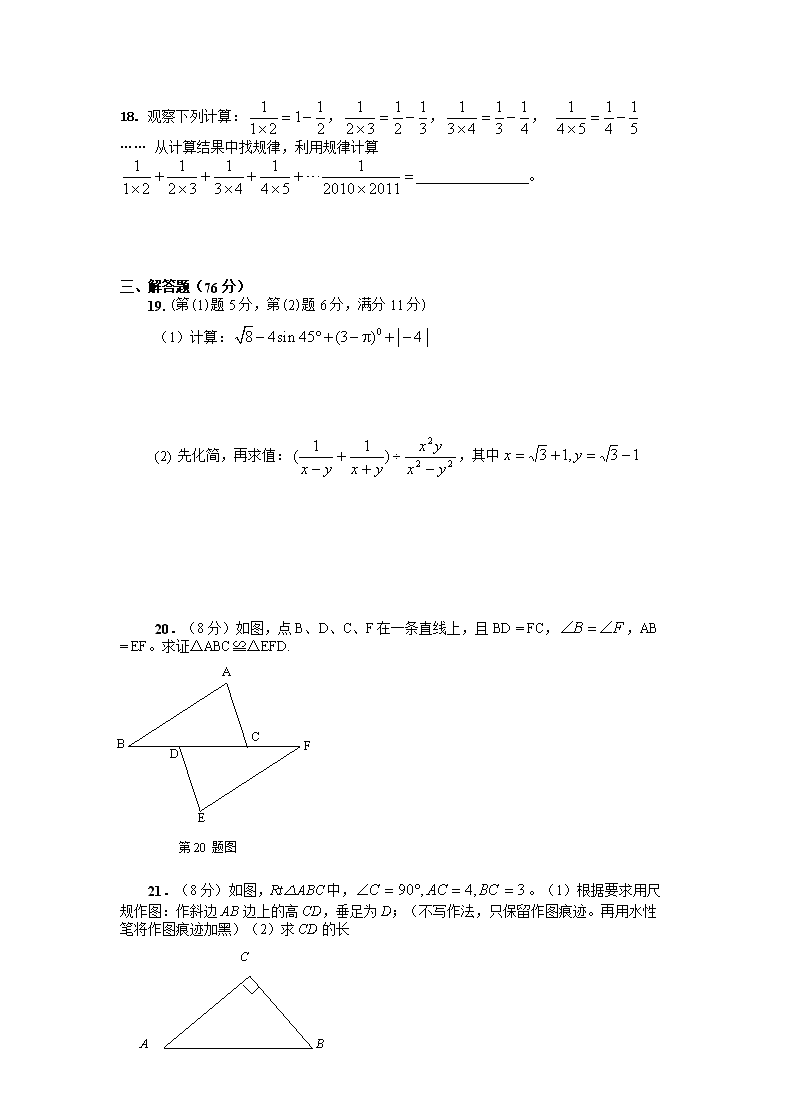
中考模拟试题 数学试题卷 时量:120分钟;满分:120分; 一、选择题(每小题3分,共24分) 1. 据《中国经济周刊》报道,上海世博会第四轮环保活动投资总金额高达820亿元,其中820亿用科学记数法表示为( ) A. B. C. D. 2. 下列计算正确的是( ) A. B. C. D. 3. 如图,△ABC中,点DE分别是ABAC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③.其中正确的有( ) A.3个 B.2个 C.1个 D.0个 4. 如图是由大小一样的小正方块摆成的立体图形的三视图,它共用( )个小正方块摆成。 第3题 A.5 B.8 C.7 D.6 左视图 正视图 俯视图 第4题 第5题 5. 如图,△ABC的三个顶点分别在正方形网格的格点上,则的值是 ( ) A. B. C. D. 6. 已知⊙和⊙相切,两圆的圆心距为9cm,⊙的半径为4cm,则⊙的半径为( ) A.5cm B.13cm C.9 cm 或13cm D.5cm 或13cm 7. 近年来,全国房价不断上涨,某市2011年5月份的房价平均每平方米为3600元, 比2009年同期的房价平均每平方米上涨了2000元,假设这两年该市房价的平均增长率均为,则关于的方程为( ) A. B. C. D. 8. 设、是常数,且,抛物线为下图中四个图象之一,则的值为( ) y x O y x O y x O 1 -1 y x O 1 -1 A. 6或-1 B. -6或1 C. 6 D. -1 二、填空题(每小题2分,共20分) 9.2的倒数是 。 10. 有意义,则实数x的取值范围是 。 11. 一组数据5,-2,3,x,3,-2,若每个数据都是这组数据的众数,则这组数据的平均数是 。 12. 方程组的解是 第13题图 13. 如图,中,,的平分线交于,若,则点到的距离是 。 14. 三角形的每条边的长都是方程的根,则三角形的周长是 。 15.菱形在平面直角坐标系中的位置如图所示,若,,则点的坐标是 。 第15题 第16题 y x O P 2 a 第17题 16. 将一副直角三角板如图放置,使含30°角的三角板的段直角边和含45°角的三角板的一条直角边重合,则∠1的度数为______________。 17. 如图,直线:与直线:相交于点,则关于的不等式的解集为 。 18. 观察下列计算:,,, …… 从计算结果中找规律,利用规律计算 。 三、解答题(76分) 19. (第(1)题5分,第(2)题6分,满分11分) (1)计算: (2) 先化简,再求值:,其中 20.(8分)如图,点B、D、C、F在一条直线上,且BD = FC,,AB = EF。求证△ABC≌△EFD. F A B C D E 第20题图 21.(8分)如图,Rt△ABC中,。(1)根据要求用尺规作图:作斜边AB边上的高CD,垂足为D;(不写作法,只保留作图痕迹。再用水性笔将作图痕迹加黑)(2)求CD的长 C B A 第21题图 22. (9分)已知:如图,在平面直角坐标系中,直线与轴交于点,与反比例函数在第一象限内的图象交于点,连结,若.(1)求该反比例函数的解析式和直线的解析式;(2)若直线与轴的交点为,求△的面积. 第22题图 A B C O x y 23.(8分)“校园手机”现象越来越受到社会的关注.“五一”期间,小记者随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图: (1)求这次调查的家长人数,并补全图①;(2)求图②中表示家长“赞成”的圆心角的度数; (3)从这次接受调查的学生中,随机抽查一个,恰好是“无所谓”态度的学生的概率是多少? 家长对中学生带手机 的态度统计图 学生及家长对中学生带手机的态度统计图 第23题图 图① 图② 24. (9分)某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.(1)甲、乙工程队每天各能铺设多少米?(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量(以百米为单位)的方案有几种?请你帮助设计出来. 25. (10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:(1)是的中点;(2)△∽△;(3)。 O D B C A E 第26题图 26. (12分) 如图,已知抛物线交轴于A、B两点,交轴于点C,抛物线的对称轴交轴于点E,点B的坐标为(,0). (1)求抛物线的对称轴及点A的坐标; (2)在平面直角坐标系中是否存在点P,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由; (3)连结CA与抛物线的对称轴交于点D,在抛物线上是否存在点M,使得直线CM把四边形DEOC 分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由. 参考答案 一、选择题 1.B 2. C 3.A 4. D 5.A 6.D 7. C 8. D 二、填空题 9. 10. 11.2 12. 13.3 14.6或10或12. 15. 16. 17。 18。 三、解答题 19.解:(1)原式 (2)原式 当时 原式 20.证明:∵BD = FC∴ 在△ABC和△EFD中 ∴△ABC≌△EFD (SAS) 21.解:(1)略 (2),根据面积相等有 ABCD=ACBC 所以CD= 22.解:(1)由,得 . ∵点在第一象限内,. ∴.∴. ∴点的坐标是. 设该反比例函数的解析式为. 将点的坐标代入,得 , ∴.∴反比例函数的解析式为:. 设直线的解析式为. 将点,的坐标分别代入,得 解得 ∴直线的解析式为.) (2)在中,令,得. ∴点的坐标是.∴.∴. 23.解:(1)这次调查的家长人数 (补全统计图略) (2)表示家长“赞成”的圆心角的度数 (3)恰好是“无所谓”态度的学生的概率是 24.(1)解:设甲工程队每天能铺设米,则乙工程队每天能铺设()米. 根据题意得:.解得. 检验: 是原分式方程的解. 答:甲、乙工程队每天分别能铺设米和米. (2)解:设分配给甲工程队米,则分配给乙工程队()米. 由题意,得解得. 所以分配方案有3种. 方案一:分配给甲工程队米,分配给乙工程队米; 方案二:分配给甲工程队米,分配给乙工程队米; 方案三:分配给甲工程队米,分配给乙工程队米. 25.(1)证明:∵AB是⊙O的直径,∴∠ADB=90° , 即AD是底边BC上的高. 又∵AB=AC,∴△ABC是等腰三角形, ∴D是BC的中点; (2) 证明:∵∠CBE与∠CAD是同弧所对的圆周角, ∴ ∠CBE=∠CAD. 又∵ ∠BCE=∠ACD, ∴△BEC∽△ADC; (3)证明:由△BEC∽△ADC,知, 即CD·BC=AC·CE. ∵D是BC的中点,∴CD=BC. 又 ∵AB=AC,∴CD·BC=AC·CE=BC ·BC=AB·CE 即BC=2AB·CE. 26.解:(1)① 对称轴 ② 当时,有 解之,得 , ∴ 点A的坐标为(,0). (2)满足条件的点P有3个,分别为(,3),(2,3),(,).) (3)存在.) 当时, ∴ 点C的坐标为(0,3) ∵ DE∥轴,AO3,EO2,AE1,CO3 ∴ ∽ ∴ 即 ∴ DE1 ∴ 4 在OE上找点F,使OF,此时2,直线CF把四边形DEOC 分成面积相等的两部分,交抛物线于点M. 设直线CM的解析式为,它经过点. 则 解之,得 ∴ 直线CM的解析式为 查看更多