- 2021-05-10 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
20125月中考复习数学压轴题练习1
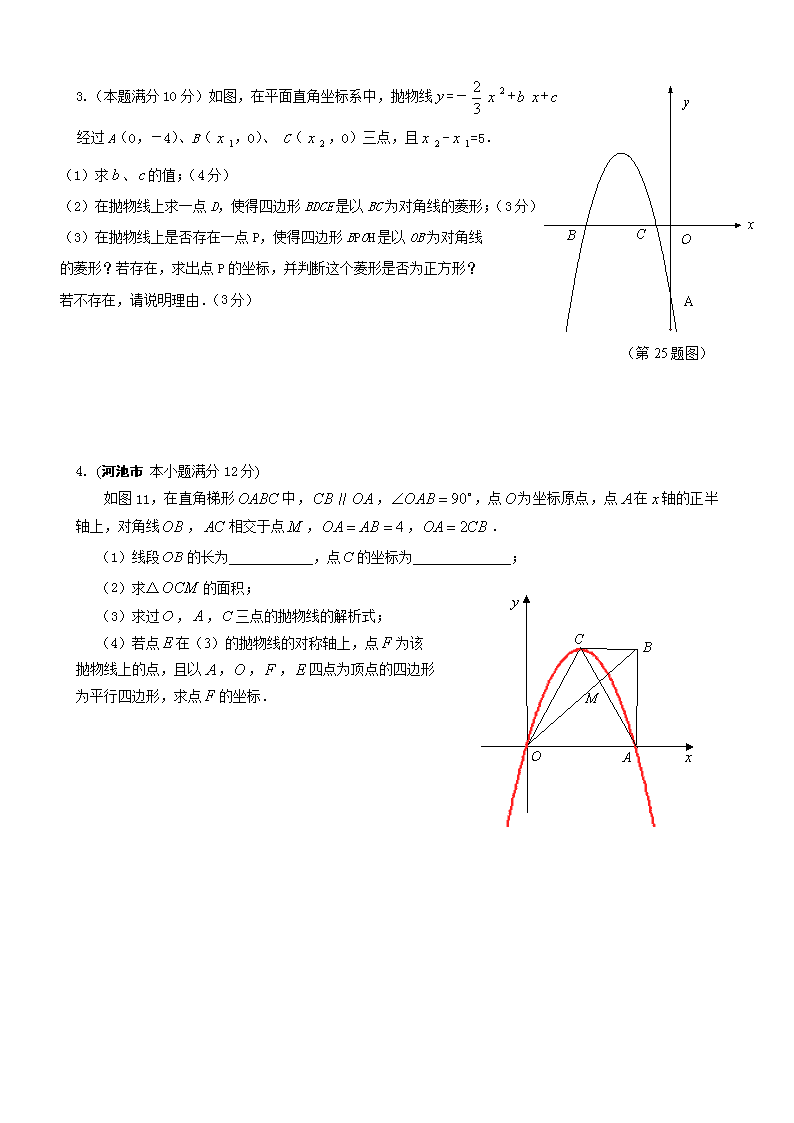
中考数学压轴题汇编(1) 1、如图,抛物线交轴于A、B两点,交轴于点C,点P是它的 顶点,点A的横坐标是3,点B的横坐标是1. (1)求、的值; (2)求直线PC的解析式; (3)请探究以点A为圆心、直径为5的圆与直线 PC的位置关系,并说明理由.(参考数:,,) 2、(湖北荆门)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合. (1)设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值; (2)如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式; 图2 图1 (3)在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标. (第25题图) A x y B C O 3.(本题满分10分)如图,在平面直角坐标系中,抛物线=-++ 经过A(0,-4)、B(,0)、 C(,0)三点,且-=5. (1)求、的值;(4分) (2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3分) (3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线 的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形? 若不存在,请说明理由.(3分) 4. (河池市 本小题满分12分) 如图11,在直角梯形中,∥,,点为坐标原点,点在轴的正半轴上,对角线,相交于点,,. (1)线段的长为 ,点的坐标为 ; M C B O A (2)求△的面积; (3)求过,,三点的抛物线的解析式; (4)若点在(3)的抛物线的对称轴上,点为该 抛物线上的点,且以,,,四点为顶点的四边形 为平行四边形,求点的坐标. 5、(2010•重庆)已知:如图(1),在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止. (1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围; (2)在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标; (3)如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由. 1、如图,抛物线交轴于A、B两点,交轴于点C,点P是它的 顶点,点A的横坐标是3,点B的横坐标是1. (1)求、的值; (2)求直线PC的解析式; (3)请探究以点A为圆心、直径为5的圆与直线 PC的位置关系,并说明理由.(参考数:,,) 解: (1)由已知条件可知: 抛物线经过A(-3,0)、B(1,0)两点. ∴ 解得 . (2) ∵, ∴ P(-1,-2),C. 设直线PC的解析式是,则 解得. ∴ 直线PC的解析式是. 说明:只要求对,不写最后一步,不扣分. (3) 如图,过点A作AE⊥PC,垂足为E. 设直线PC与轴交于点D,则点D的坐标为(3,0).在Rt△OCD中,∵ OC=,, ∴ . …………8分 ∵ OA=3,,∴AD=6. …………9分∵ ∠COD=∠AED=90o,∠CDO公用, ∴ △COD∽△AED.∴ , 即. ∴ . ∵ , ∴ 以点A为圆心、直径为5的圆与直线PC相离. ………12分 2、(湖北荆门)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合. (1)设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值; (2)如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式; 图2 图1 (3)在(2)的情况下,在该抛物线上是否存在点Q,使△PEQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标. 解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠BPE=90°.∴∠OPE+∠APB=90°.又∠APB+∠ABP=90°,∴∠OPE=∠PBA. ∴Rt△POE∽Rt△BPA.…………………………………………………………2分 ∴.即.∴y=(0<x<4). 且当x=2时,y有最大值.…………………………………………………4分 (2)由已知,△PAB、△POE均为等腰三角形,可得P(1,0),E(0,1),B(4,3).……6分 设过此三点的抛物线为y=ax2+bx+c,则∴ A x y B C O y=.… (3)由(2)知∠EPB=90°,即点Q与点B重合时满足条件.……………………9分 直线PB为y=x-1,与y轴交于点(0,-1).将PB向上平移2个单位则过点E(0,1), ∴该直线为y=x+1.…由得∴Q(5,6). 故该抛物线上存在两点Q(4,3)、(5,6)满足条件. 12 3.(本题满分10分)如图,在平面直角坐标系中,抛物线=-++ 经过A(0,-4)、B(,0)、 C(,0)三点,且-=5. (1)求、的值;(4分) (2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;(3分) (3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线 的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形? 若不存在,请说明理由.(3分) 解:(1)∵抛物线=-++经过点A(0,-4), ∴=-4 又由题意可知,、是方程-++=0的两个根, ∴+=, =-=6 由已知得(-)=25 又(-)=(+)-4=-24 ∴ -24=25 解得=±当=时,抛物线与轴的交点在轴的正半轴上,不合题意,舍去.∴=-. (2)∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上, 5分 又∵=---4=-(+)+ 6分 ∴抛物线的顶点(-,)即为所求的点D. 7分 (3)∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(-6,0), 根据菱形的性质,点P必是直线=-3与 抛物线=---4的交点, 8分 ∴当=-3时,=-×(-3)-×(-3)-4=4, ∴在抛物线上存在一点P(-3,4),使得四边形BPOH为菱形. 9分 M C B O A 图11 四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(-3,3),但这一点不在抛物线上. 10分 4. (河池市 本小题满分12分) 如图11,在直角梯形中,∥,,点为 坐标原点,点在轴的正半轴上,对角线,相交于点, ,. (1)线段的长为 ,点的坐标为 ; (2)求△的面积; (3)求过,,三点的抛物线的解析式; (4)若点在(3)的抛物线的对称轴上,点为该 抛物线上的点,且以,,,四点为顶点的四边形 为平行四边形,求点的坐标. 解:(1)4 ;. …………………(2分) (2)在直角梯形OABC中,OA=AB=4, ∵ ∥ ∴ △OAM∽△BCM ………(3分) 又 ∵ OA=2BC ∴ AM=2CM ,CM=AC ………………(4分) M C B O A D 所以 ………(5分) (注:另有其它解法同样可得结果,正确得本小题满分.) (3)设抛物线的解析式为 由抛物线的图象经过点,,.所以 ……………………………(6分) 解这个方程组,得,, ………………(7分) 所以抛物线的解析式为 ………………(8分) (4)∵ 抛物线的对称轴是CD, ① 当点E在轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合,点F的坐标即为点; …(9分) ② 当点E在轴的下方,点F在对称轴的右侧,存在平行四边形, ∥,且,此时点F的横坐标为6,将代入,可得.所以. ………………………………………(11分) 同理,点F在对称轴的左侧,存在平行四边形,∥,且,此时点F的横坐标为,将代入,可得.所以.(12分) 综上所述,点F的坐标为,. ………(12分) 5、(2010•重庆)已知:如图(1),在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止. (1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系,并写出自变量t的取值范围; (2)在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标; (3)如图(2),现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由. 解答:解:(1)过点C作CD⊥OA于点D.(如图) ∵OC=AC,∠ACO=120°, ∴∠AOC=∠OAC=30°. ∵OC=AC,CD⊥OA,∴OD=DA=1. 在Rt△ODC中,OC===(1分) (i)当0<t<时,OQ=t,AP=3t,OP=OA﹣AP=2﹣3t. 过点Q作QE⊥OA于点E.(如图) 在Rt△OEQ中,∵∠AOC=30°,∴QE=OQ=, ∴S△OPQ=OP•EQ=(2﹣3t)•=﹣+t, 即S=﹣+t;(3分) (ii)当<t≤时(如图) OQ=t,OP=3t﹣2. ∴∠BOA=60°,∠AOC=30°,∴∠POQ=90°. ∴S△OPQ=OQ•OP=t•(3t﹣2)=﹣t, 即S=﹣t; 故当0<t<时,S=﹣+t,当≤t<时,S=﹣t(5分) (2)D(,1)或(,0)或(,0)或(,)(9分) (3)△BMN的周长不发生变化.理由如下: 延长BA至点F,使AF=OM,连接CF.(如图) 又∵∠MOC=∠FAC=90°,OC=AC, ∴△MOC≌△FAC, ∴MC=CF,∠MCO=∠FCA.(10分) ∴∠FCN=∠FCA+∠NCA=∠MCO+∠NCA =∠OCA﹣∠MCN=60°, ∴∠FCN=∠MCN. 又∵MC=CF,CN=CN,∴△MCN≌△FCN,∴MN=NF.(11分) ∴BM+MN+BN=BM+NF+BN=BO﹣OM+BA+AF=BA+BO=4.∴△BMN的周长不变,其周长 为4.查看更多