- 2021-05-10 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018中考总复习平行四边形专题
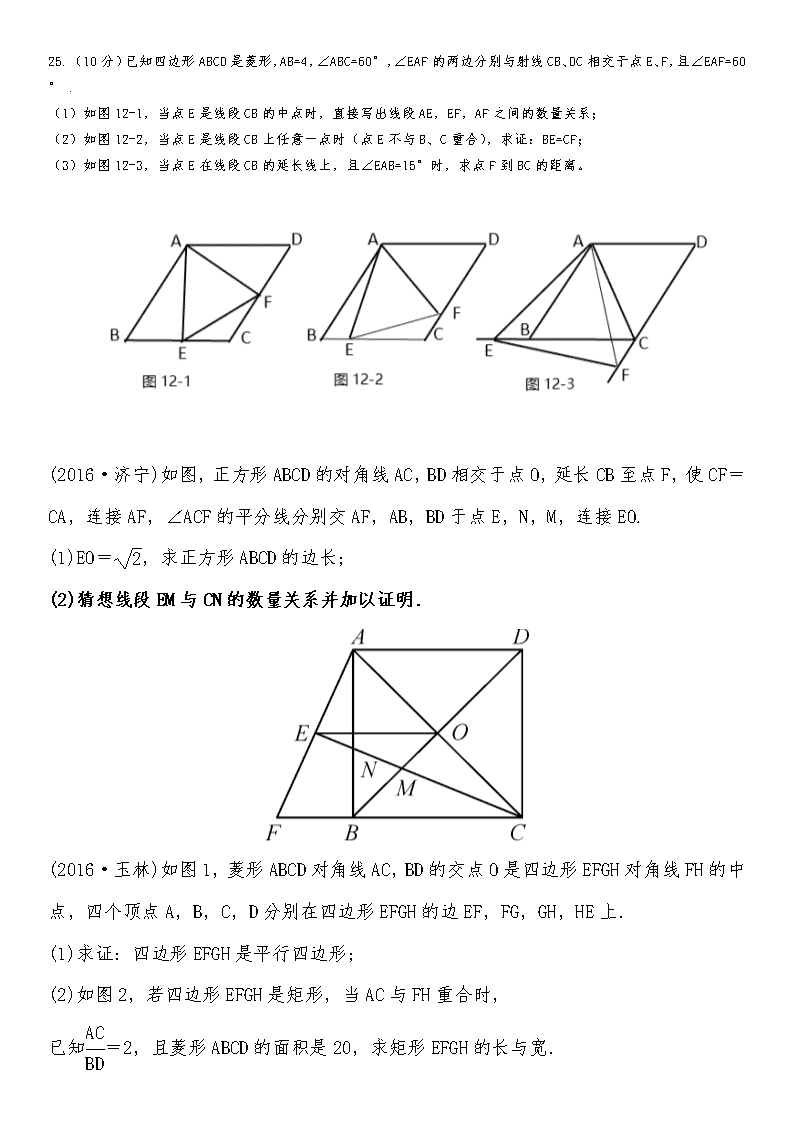
25.(10分)已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60° . (1)如图12-1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系; (2)如图12-2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF; (3)如图12-3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离。 (2016·济宁)如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO. (1)EO=,求正方形ABCD的边长; (2)猜想线段EM与CN的数量关系并加以证明. (2016·玉林)如图1,菱形ABCD对角线AC,BD的交点O是四边形EFGH对角线FH的中点,四个顶点A,B,C,D分别在四边形EFGH的边EF,FG,GH,HE上. (1)求证:四边形EFGH是平行四边形; (2)如图2,若四边形EFGH是矩形,当AC与FH重合时, 已知=2,且菱形ABCD的面积是20,求矩形EFGH的长与宽. 9.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于( ) A.B.C.5 D.4 17.如图,在△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= ﹣1 . 【考点】旋转的性质. 【分析】连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD﹣C′D计算即可得解. 【解答】解:如图,连接BB′, ∵△ABC绕点A顺时针方向旋转60°得到△AB′C′, ∴AB=AB′,∠BAB′=60°, ∴△ABB′是等边三角形, ∴AB=BB′, 在△ABC′和△B′BC′中, , ∴△ABC′≌△B′BC′(SSS), ∴∠ABC′=∠B′BC′, 延长BC′交AB′于D, 则BD⊥AB′, ∵∠C=90°,AC=BC=, ∴AB==2, ∴BD=2×=, C′D=×2=1, ∴BC′=BD﹣C′D=﹣1. 故答案为:﹣1. 【点评】本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出BC′在等边三角形的高上是解题的关键,也是本题的难点. 24.如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6. (1)求∠EPF的大小; (2)若AP=10,求AE+AF的值; (3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值. 【考点】菱形的性质;几何问题的最值. 【分析】(1)根据锐角三角函数求出∠FPG,最后求出∠EPF. (2)先判断出Rt△PME≌Rt△PNF,再根据锐角三角函数求解即可, (3)根据运动情况及菱形的性质判断求出AP最大和最小值. 【解答】解:(1)过点P作PG⊥EF于点G,如图1所示. ∵PE=PF=6,EF=6, ∴FG=EG=3,∠FPG=∠EPG=∠EPF. 在Rt△FPG中,sin∠FPG===, ∴∠FPG=60°, ∴∠EPF=120°. (2)过点P作PM⊥AB于点M,作PN⊥AD于点N,如图2所示. ∵AC为菱形ABCD的对角线, ∴∠DAC=∠BAC,AM=AN,PM=PN. 在Rt△PME和Rt△PNF中,PM=PN,PE=PF, ∴Rt△PME≌Rt△PNF, ∴ME=NF. 又AP=10,∠PAM=∠DAB=30°, ∴AM=AN=APcos30°=10×=5, ∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=10. (3)如图, 当△EFP的三个顶点分别在AB,AD,AC上运动,点P在P1,P之间运动, ∴P1O=PO=3,AO=9, ∴AP的最大值为12,AP的最小值为6, 【点评】此题是菱形的性质题,主要考查了菱形的性质,锐角三角函数,特殊角的三角函数,解本题的关键是作出辅助线. (2015·柳州T24·10分)如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12 cm,BC=18 cm,点P从点A出发以2 cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1 cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒. (1)从运动开始,当t取何值时,PQ∥CD? (2)从运动开始,当t取何值时,△PQC为直角三角形? 【思路点拨】 (1)已知AD∥BC,添加PD=CQ,即可判断以P,Q,D,C为顶点的四边形是平行四边形;(2)点P处可能为直角,点Q处也可能是直角,故需要分类讨论求解. 解:(1)当PQ∥CD时,四边形PDCQ是平行四边形,此时PD=QC,2分 ∴12-2t=t.解得t=4. ∴当t=4时,PQ∥CD.4分 (2)过D点作DF⊥BC于F. ∴DF=AB=8,FC=BC-AD=18-12=6, 由勾股定理得CD=10. ①当PQ⊥BC时,则BQ+CQ=18, 即2t+t=18,解得t=6;6分 ②当QP⊥PC时,此时P一定在DC上, CP1=10+12-2t=22-2t,CQ1=t, 易知△CDF∽△CQ1P1. ∴=.解得t=;8分 ③当PC⊥BC时, ∵∠DCB<90°, ∴此种情形不存在. 综上所述,当t=6或时,△PQC是直角三角形.10分 .(2014·柳州)如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q. (1)求线段PQ的长; (2)问:点P在何处时,△PFD ∽△BFP,并说明理由. 解:(1)根据题意,得 PD=PE,∠DPE=90°, ∴∠APD+∠QPE=90°. ∵四边形ABCD是正方形,∴∠A=90°. ∴∠ADP+∠APD=90°. ∴∠ADP=∠QPE. ∵EQ⊥AB,∴∠A=∠Q=90°. 在△ADP和△QPE中, ∴△ADP≌△QPE(AAS). ∴PQ=AD=1. (2)当P点为AB的中点时,△PFD∽△BFP. 理由:∵∠ADP=∠BPF,∠A=∠FBP, ∴△DAP∽△PBF.∴=. ∵P点为AB的中点, ∴PA=AB=PB. ∴=,即=. 又∵∠PBF=∠DPF, ∴△PFD∽△BFP. 2.(2017·海南)如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连接CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G. (1)求证:△CDE≌△CBF; (2)当DE=时,求CG的长; (3)连接AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由. 解:(1)证明:在正方形ABCD中,DC=BC,∠D=∠ABC=∠DCB=90°, ∴∠CBF=180°-∠ABC=90°,∠DCE+∠ECB=∠DCB=90°. ∵CF⊥CE,∴∠ECF=90°. ∴∠BCF+∠ECB=∠ECF=90°. ∴∠DCE=∠BCF. 在△CDE和△CBF中, ∴△CDE≌△CBF(ASA). (2)在正方形ABCD中,AD∥BC, ∴△GBF∽△EAF. ∴=. 由(1)知△CDE≌△CBF, ∴BF=DE=. ∵正方形的边长为1, ∴AF=AB+BF=,AE=AD-DE=. ∴=.∴BG=. ∴CG=BC-BG=. (3)不能.理由:若四边形CEAG是平行四边形,则必须满足AE∥CG,AE=CG, ∴AD-AE=BC-CG.∴DE=BG. 由(1)知△CDE≌△CBF, ∴DE=BF,CE=CF. ∴△GBF和△ECF是等腰直角三角形. ∴∠GFB=45°,∠CFE=45°. ∴∠CFA=∠GFB+∠CFE=90°. 此时点F与点B重合,点D与点E重合,与题目条件不符, ∴点E在运动过程中,四边形CEAG不能是平行四边形. 4.(2017·贵港)已知在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处. (1)如图1,若点D是AC中点,连接PC. ①写出BP,BD的长; ②求证:四边形BCPD是平行四边形; (2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长. 解:(1)①BP=2,BD=2. ②证明:延长BD至E, ∵D是AC边的中点,AC=4,BC=2, ∴DC=AD=BC. 又∵∠ACB=90°, ∴△BDC是等腰直角三角形, ∴∠BDC=∠ADE=45°. 由折叠(轴对称)性质可知, ∠EDP=∠ADE=45°,PD=AD=2, ∴∠PDA=90°. ∴PD∥BC,且PD=BC=2. ∴四边形BCPD是平行四边形. (2)连接AP并延长与BC的延长线交于点F,延长BD与AP交于点E, 由折叠(轴对称)性质可知, PD=AD,∠PDE=∠ADE,BE⊥AP,PE=AE. ∵BD=AD, ∴在Rt△BDC中,由勾股定理,得 BD2=(4-BD)2+22, ∴BD=. ∵AD=BD,∠ADE=∠BDC, ∴Rt△PDE≌Rt△ADE≌Rt△BDC. ∴PA=2BC=4,∠FAC=∠DBC. ∴Rt△FAC∽Rt△DBC. ∴=. ∴FA=5,则PF=1. ∵PH⊥BC,∴PH∥AC. ∴Rt△FPH∽Rt△FAC. ∴=. ∴PH=.查看更多