2014重庆市中考数学试卷B卷

2014重庆市中考数学试卷B卷

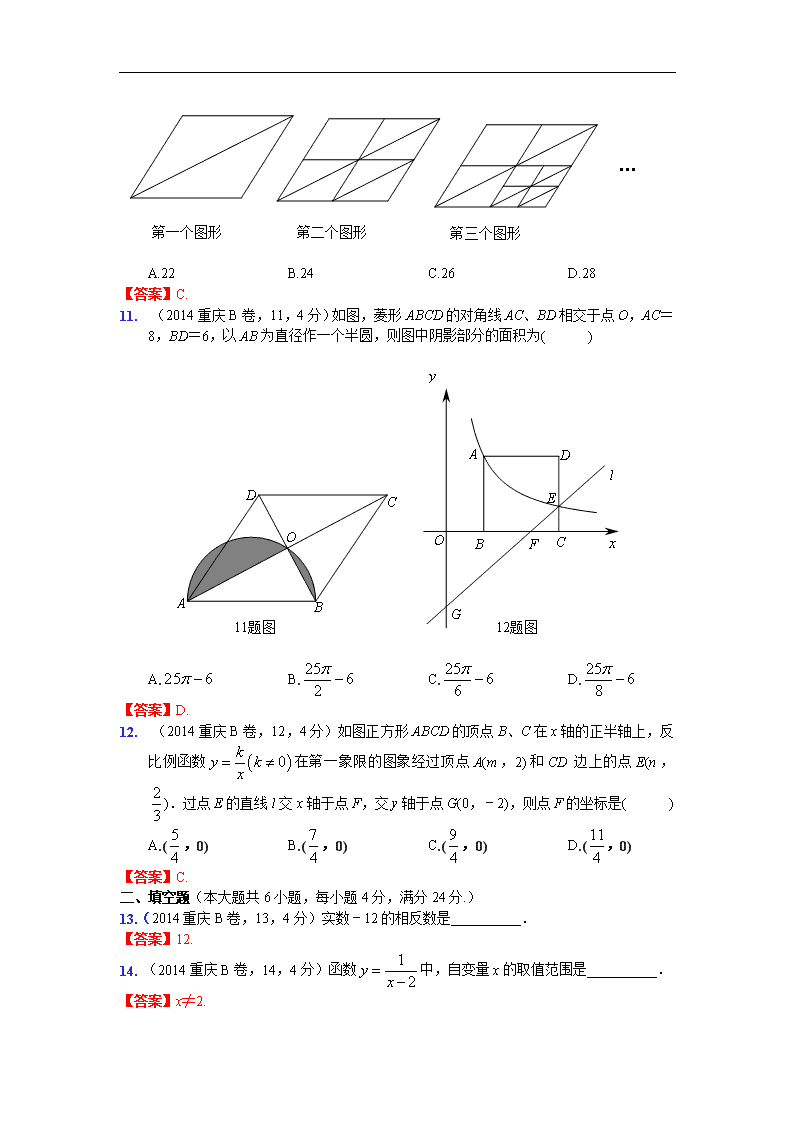
‎2014年重庆市中考数学试卷（B卷）‎ ‎（满分150分，考试时间120分钟）‎ 一、选择题（本大题共12小题，每小题4分，满分24分，在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1.（2014重庆B卷，1，4分）某地连续四天每天的平均气温分别是：1℃，﹣1℃，0℃，2℃，则平均气温中最低的是（ ）‎ ‎ A.﹣1℃ B.0℃ C.1℃ D.2℃‎ ‎【答案】A.‎ ‎2. （2014重庆B卷，2，4分）计算5x2－2x2的结果是（ ）‎ ‎ A.3 B.3x C.3x2 D.3x4‎ ‎【答案】C.‎ ‎3. （2014重庆B卷，3，4分）如图，△ABC∽△DEF，相似比为1:2，若BC＝1，则EF的长是（ ）‎ ‎ A.1 B.2 C.3 D.4‎ ‎【答案】B.‎ ‎4. （2014重庆B卷，4，4分）如图，直线AB∥CD，直线EF分别交AB、CD于点E、F，若∠AEF＝50°，则∠EFC的大小是（ ）‎ ‎ A.40° B.50° C.120° D.130°‎ ‎【答案】D.‎ ‎5. （2014重庆B卷，5，4分）某校将举办一场“中国汉字听写大赛”，要求每班推选一名同学参加比赛，为此，初三（1）班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是96分，甲的成绩的方差是0.2，乙的成绩的方差是0.8，根据以上数据，下列说法正确的是（ ）‎ A.甲的成绩比乙的成绩稳定 B.乙的成绩比甲的成绩稳定 C.甲、乙两人的成绩一样稳定 D.无法确定甲、乙的成绩谁更稳定 ‎ ‎【答案】A.‎ ‎6. （2014重庆B卷，6，4分）若点(3，1)在一次函数y＝kx－2(k≠0)的图象上，则k的值是( )‎ ‎ A.5 B.4 C.3 D.1‎ ‎【答案】D.‎ ‎7. （2014重庆B卷，7，4分）分式方程的解是( )‎ ‎ A.x＝1 B.x＝﹣1 C.x＝3 D.x＝﹣3‎ ‎【答案】C.‎ ‎8. jscm（2014重庆B卷，8，4分）如图，在矩形ABCD中，对角线AC、BD相交于点O，∠ACB＝30°，则∠AOB的大小为( )‎ ‎ A.30° B.60° ‎ C.90° D.120°‎ ‎【答案】B.‎ ‎9. jscm（2014重庆B卷，9，4分）夏天到了，某小区准备开放游泳池，物业管理处安排一名清洁工对一个无水的游泳池进行清洗．该工人先打开一个进水馆，蓄了少量水后关闭进水管并立即进行清洗，一段时间后，再同时打开两个出水管将池内的水放完，随后将两个出水管关闭，并同时打开两个进水管将水蓄满．已知每个进水管的进水进度与每个出水管的出水速度相同，从工人最先打开一个进水管开始，所用的时间为x，游泳池内的蓄水量为y，则下列各图中能够反映y与x的函数关系大致图象是( )‎ ‎【答案】C.‎ ‎10. jscm（2014重庆B卷，10，4分）下列图形都是按照一定规律组成，第一个图形中共有2个三角形，第二个图形中共有8个三角形，第三个图形中共有14个三角形，…，依此规律，第五个图形中三角形的个数是( )‎ A.22 B.24 C.26 D.28‎ ‎【答案】C.‎ ‎11. jscm（2014重庆B卷，11，4分）如图，菱形ABCD的对角线AC、BD相交于点O，AC＝8，BD＝6，以AB为直径作一个半圆，则图中阴影部分的面积为( )‎ ‎ A. B. C. D.‎ ‎【答案】D.‎ ‎12. jscm（2014重庆B卷，12，4分）如图正方形ABCD的顶点B、C在x轴的正半轴上，反比例函数在第一象限的图象经过顶点A(m，2)和CD边上的点E(n，)．过点E的直线l交x轴于点F，交y轴于点G(0，﹣2)，则点F的坐标是( )‎ ‎ A.(，0) B.(，0) C.(，0) D.(，0)‎ ‎【答案】C.‎ 二、填空题（本大题共6小题，每小题4分，满分24分.）‎ ‎13.（2014重庆B卷，13，4分）实数﹣12的相反数是__________．‎ ‎【答案】12.‎ ‎14. （2014重庆B卷，14，4分）函数中，自变量x的取值范围是__________．‎ ‎【答案】x≠2.‎ ‎15. （2014重庆B卷，15，4分）在2014年重庆市初中毕业生体能测试中，某校初三有7名同学的体能测试成绩(单位：分)如下：50，48，47，50，48，49，48．这组数据的众数是______________．‎ ‎【答案】48‎ ‎16. （2014重庆B卷，16，4分）如图，C为⊙O外一点，CA与⊙O相切，切点为A，AB为⊙O的直径，连接CB．若⊙O的半径为2，∠ABC＝60°，则BC＝______________．‎ ‎【答案】8‎ ‎17. （2014重庆B卷，17，4分）在一个不透明的盒子装着4个分别标有数字1，2，3，4的小球，它们除数字不同外其余完全相同，搅匀后从盒子里随机取出1个小球，将该小球上的数字作为a的值，则使关于x的不等式组只有一个整数解的概率为___________．‎ ‎【答案】.‎ ‎18. （2014重庆B卷，18，4分）如图，在边长为的正方形ABCD中，E是AB边上一点，G是AD延长线一点，BE＝DG，连接EG，CF⊥EG交EG于点H，交AD于点F，连接CE、BH．若BH＝8，则FG＝_____________．‎ ‎【答案】.‎ 三、解答题（本大题共2个小题，每小题7分，共14分，解答应写出文字说明、证明过程或演算步骤）‎ ‎19. jscm（2014重庆B卷，19，7分）计算：‎ ‎【答案】原式＝9＋2－1－3＋2＝9.‎ ‎20.jscm（2014重庆B卷，20，7分）如图，在△ABC中，CD⊥AB，垂足为D．若AB＝12，CD＝6，tanA＝，求sinB＋cosB的值．‎ ‎【答案】解：在Rt△ACD中，CD＝6，tanA＝，∴AD＝4，∴BD＝AB·AD＝8，‎ 在Rt△BCD中，BC＝＝10，∴sinB＝＝，cosB＝‎ ‎∴sinB＋cosB＝‎ 四、解答题（本大题共4个小题，每小题10分，共40分，解答应写出文字说明、证明过程或演算步骤）‎ ‎21. （2014重庆B卷，21，10分）先化简，再求值：，其中x是方程的解．‎ ‎【答案】原式＝＝＝，‎ 解方程得：，‎ 当时，原式＝‎ ‎22. （2014重庆B卷，22，10分）重庆市某餐饮文化公司准备承办“重庆火锅美食文化节”．为了解市民对火锅的喜爱程度，该公司设计了一个调查问卷，将喜爱程度分为A(非常喜欢)、B(喜欢)、C(不太喜欢)、D(很不喜欢)四种类型，并派业务员进行市场调查．其中一个业务员小丽在解放碑步行街对市民进行了随机调查，并根据调查结果制成了如下两幅不完整的统计图．请结合统计图所给信息解答下列问题：‎ ‎ (1)在扇形统计图中C所占的百分比是__________；小丽本次抽样调查的人数共有__________人；请将折线统计图补充完整；‎ ‎ (2)为了解少数市民很不喜欢吃火锅的原因，小丽决定在上述调查中从“很不喜欢”吃火锅的市民里随机选出两位进行电话回访，请你用列表法或画树状图的方法，求所选出的两位市民恰好都是男性的概率．‎ ‎【答案】解：(1)22%；50；作图略．‎ ‎(2)由图可知：很不喜欢的共有3人，其中男性人，女性人；列树状图如下：‎ 由图可知，共有6种等可能情况，其中恰好都是男性的概率(记为事件A)共有2种，即 P(A)＝．‎ ‎23.（2014重庆B卷，23，10分）某生态农业园种植的青椒除了运往市区销售外，还可以让市民亲自去生态农业园购买，已知今年5月份青椒在市区，园区的销售价格分别为6元/千克、4元/千克，今年5月份一共销售了3000千克，总销售额为16000元．‎ ‎ (1)今年5月份该青椒在市区、园区各销售了多少千克？‎ ‎ (2)6月份是青椒产出旺季，为了促乐销，生态农业园决定6月份将该青椒在市区、园区的销售价格均在今年5月份的基础上降低a%，预计这种青椒在市区、园区的销量将在今年5月份的基础上分别增长30%、20%．要使6月份该青椒的总销售额不低于18360元，则a的最大值是多少？‎ ‎【答案】解：(1)设5月份在市区销售了x千克，园区销售了y千克，由题意得：‎ 解得：‎ 答：5月份在市区销售了3000千克、园区销售了1000千克．‎ ‎(2)由题意得：‎ ‎6(1－a%)×2000(1+30%)＋(1－a%)×1000(1＋20%)≥18360，解得：a≤10．‎ 则a的最大值为10．‎ ‎24. jscm（2014重庆B卷，24，10分）如图、在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D．CG平分∠ACB交BD于点G，F为AB边上一点，边接CF，且∠ACF＝∠CBG．‎ ‎ 求证：(1)AF＝CG；‎ ‎ (2)CF＝2DE．‎ ‎【答案】解：证明：(1)∵∠ACB＝90°，CG平分∠ACB，AC＝BC．‎ ‎∴∠BCG＝∠CAB＝45°，又∵∠ACF＝∠CBG，AC＝BC，‎ ‎∴△ACF≌△CBG(ASA)，∴AF＝CG，CF＝BG．‎ ‎(2)延长CG交AB于点H．‎ ‎∵AC＝BC，CG平分∠ACB，∴CH⊥AB，H为AB中点，‎ 又∵AD⊥AB，∴CH∥AD，∴G为BD中点，∠D＝∠EGC，‎ ‎∵E为AC中点，∴AE＝EC，又∵∠AED＝∠CEG，‎ ‎∴△AED≌△CEG，∴DE＝EG，∴DG＝2DE，∴BG＝DG＝2DE，‎ 由(1)得CF＝BG，∴CF＝2DE．‎ 五、解答题（本大题共2个小题，每小题12分，共24分，解答应写出文字说明、证明过程或演算步骤）‎ ‎25. （2014重庆B卷，25，12分）如图已知抛物线与x轴交于两点(点A在点B的左边)，与y轴交于点C，连接BC．‎ ‎ (1)求A、B、C三点的坐标；‎ ‎ (2)若点P为线段BC上的一点(不与B、C重合)，PM∥y轴，且PM交抛物线于点M，‎ 交x轴于点N，当△BCM的面积最大时，求△BPN的周长；‎ ‎ (3)在(2)的条件下，当△BCM的面积最大时，在抛物线的对称轴上存在点Q，使得△CNQ 为直角三角形，求点Q的坐标．‎ ‎【答案】解：(1)设x＝0，得y＝3，∴点C坐标为(0，3)，‎ 设y＝0，得x1＝﹣1，x2＝3，∴点A的坐标为(﹣1，0)，点B的坐标为(3，0)‎ ‎(2)易求得直线BC的解析式为y＝﹣x＋3，‎ 设点P的坐标为(x，﹣x＋3)，(0＜x＜3)‎ ‎∵PM∥y轴，∴点M坐标为(x，﹣x2＋2x＋3)‎ ‎∴PM＝(﹣x2＋2x＋3)－(﹣x＋3)＝﹣x2＋3x．‎ ‎∵，∴当时，最大．‎ 此时点P的坐标为(，)，‎ ‎∴PN＝，BN＝，BP＝，∴．‎ ‎(3)抛物线的对称轴为x＝1‎ 设点Q的坐标为(1，a)，‎ ‎∴CQ2＝(a－3)2＋1＝a2－6a＋10，QN2＝a2＋，CN2＝．‎ ‎①当CQ2＝QN2＋CN2时，即∠CNQ＝90°时，‎ a2－6a＋10＝a2＋＋，解得：．‎ 此时点Q的坐标为(1，)．‎ ‎②当∠QCN＝90°时，即CQ2＋CN2＝QN2，‎ a2－6a＋10＋＝a2＋，解得：‎ 此时点Q的坐标为(1，)．‎ ‎③当∠CQN＝90°时，即CQ2＋QN2＝CN2，‎ a2－6a＋10＋a2＋＝，解得：，，‎ 此时点Q的坐标为(1，)或(1，)．‎ 综上所述，当△CNQ为直角三角形时，点Q的坐标为：(1，)或(1，)或(1，)或(1，)．‎ ‎26. （2014重庆B卷，26，12分）如图1，在中，AH⊥DC，垂足为H，AB＝，AD＝7，AH＝．现有两个动点E、F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，当点E运动到点C时，E、F两点同时停止运动．设运动时间为t秒．‎ ‎ (1)求线段AC的长；‎ ‎ (2)在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请直接写出S与 t之间的函数关系式，并写出相应的自变量t的取值范围；‎ ‎ (3)当等边△EFG的顶点E到达点C时，如图2，将△EFG绕着点C旋转一个角度α(0°＜α＜360°)．在旋转过程中，点E与点C重合，F的对应点为F’，G的对应点为G’，设直线F’G’与射线DC、射线AC分别相交于M、N两点．试问：是否存在点M、N，使得△CMN是以∠MCN为底角的等腰三角形？若存在，请求出线段CM的长度；若不存在，请说明理由．‎ ‎【答案】解：(1)在Rt△ADH中，DH2＝AD2－AH2，‎ ‎∴DH＝，HC＝DC－DH＝，∴H为DC中点，‎ 又∵AH⊥DC，∴AC＝AD＝7．‎ ‎(2)‎ ‎(3)‎ ‎①设IN＝x，CI＝IM＝y，由△AHC∽△IJC，得CM＝2CJ＝，‎ 在Rt△CNI、Rt△CNM中 ‎，解得：y＝‎ ‎∴CM＝‎ ‎②设JM＝x，CM＝y＝MN，由△CAH∽△CMI，得CN＝2CI＝‎ 在Rt△CJM、Rt△CJN中 ‎，解得：x＝，则y＝‎ ‎∴CM＝‎ 所以存在点M、N，使得△CMN是以∠MCN为底角的等腰三角形，此时CM＝或．‎