中考数学函数探究专题复习试题含解析
函数探究
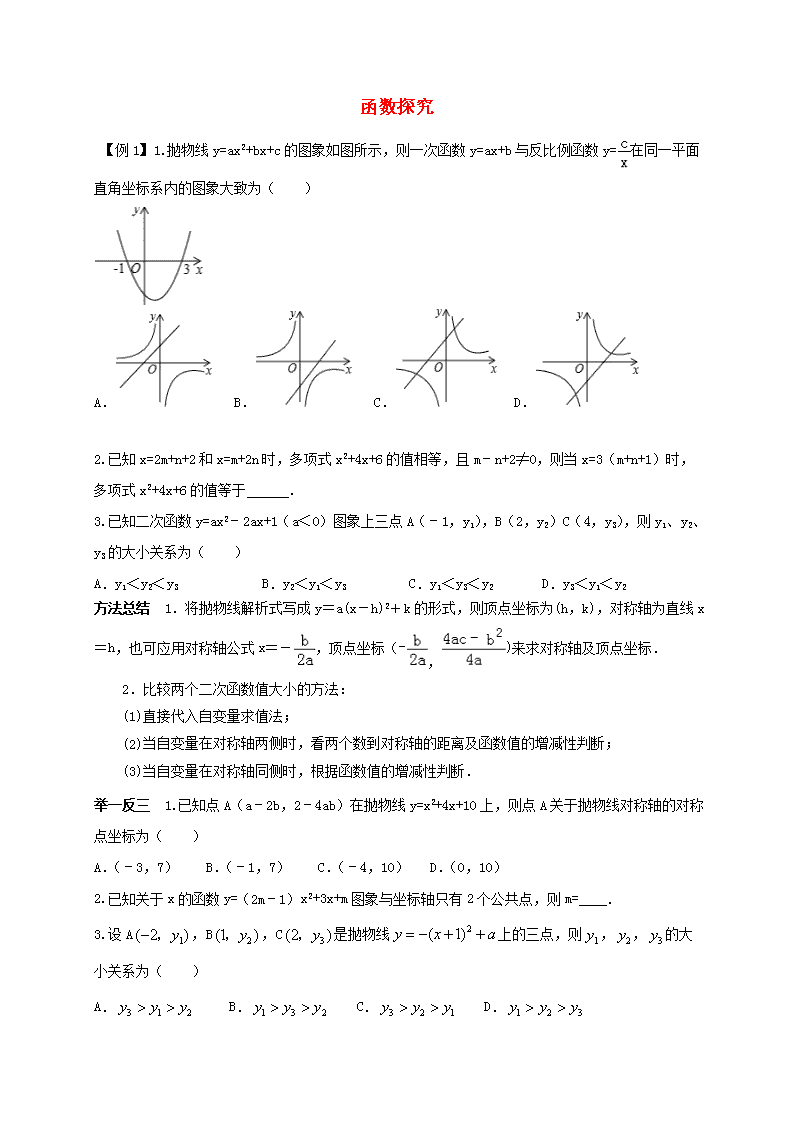
【例1】 1.抛物线y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系内的图象大致为( )
A. B. C. D.
2.已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m﹣n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+6的值等于 .
3.已知二次函数y=ax2﹣2ax+1(a<0)图象上三点A(﹣1,y1),B(2,y2)C(4,y3),则y1、y2、y3的大小关系为( )
A.y1<y2<y3 B.y2<y1<y3 C.y1<y3<y2 D.y3<y1<y2
方法总结 1.将抛物线解析式写成y=a(x-h)2+k的形式,则顶点坐标为(h,k),对称轴为直线x=h,也可应用对称轴公式x=-,顶点坐标(-,)来求对称轴及顶点坐标.
2.比较两个二次函数值大小的方法:
(1)直接代入自变量求值法;
(2)当自变量在对称轴两侧时,看两个数到对称轴的距离及函数值的增减性判断;
(3)当自变量在对称轴同侧时,根据函数值的增减性判断.
举一反三 1.已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7) B.(﹣1,7) C.(﹣4,10) D.(0,10)
2.已知关于x的函数y=(2m﹣1)x2+3x+m图象与坐标轴只有2个公共点,则m= .
3.设A,B,C是抛物线上的三点,则,,的大小关系为( )
A. B. C. D.
考点二、二次函数系数的符号及其之间的关系
【例2】 二次函数y=ax2+bx+c的图象如图所示,给出下列结论:
①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣;④3|a|+|c|<2|b|.
其中正确的结论是 (写出你认为正确的所有结论序号).
方法总结 根据二次函数的图象确定有关代数式的符号,是二次函数中的一类典型的数形结合问题,具有较强的推理性.解题时应注意a决定抛物线的开口方向,c决定抛物线与y轴的交点,抛物线的对称轴由a,b共同决定,b2-4ac决定抛物线与x轴的交点情况.当x=1时,决定a+b+c的符号,当x=-1时,决定a-b+c的符号.在此基础上,还可推出其他代数式的符号.运用数形结合的思想更直观、更简捷.
举一反三 1.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b2﹣4ac>0; ②4a+c>2b; ③(a+c)2>b2; ④x(ax+b)≤a﹣b.
其中正确结论的是 .(请把正确结论的序号都填在横线上)
2.一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
考点三、二次函数图象的平移
【例3】二次函数y=-2x2+4x+1的图象怎样平移得到y=-2x2的图象( )
A.向左平移1个单位,再向上平移3个单位
B.向右平移1个单位,再向上平移3个单位
C.向左平移1个单位,再向下平移3个单位
D.向右平移1个单位,再向下平移3个单位
方法总结 二次函数图象的平移实际上就是顶点位置的变换,因此先将二次函数解析式转化为顶点式确定其顶点坐标,然后按照“左加右减、上加下减”的规律进行操作.
举一反三 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数解析式是( )
A.y=(x-1)2+2 B.y=(x+1)2+2 C.y=(x-1)2-2 D.y=(x+1)2-2
考点四、确定二次函数的解析式
【例4】如图,四边形ABCD是菱形,点D的坐标是(0,),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
(1)求A,B,C三点的坐标;
(2)求经过A,B,C三点的抛物线的解析式.
方法总结 用待定系数法求二次函数解析式,需根据已知条件,灵活选择解析式:若已知图象上三个点的坐标,可设一般式;若已知二次函数图象与x轴两个交点的横坐标,可设交点式;若已知抛物线顶点坐标或对称轴与最大(或小)值,可设顶点式.
举一反三 已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为 .
考点五、二次函数的实际应用
【例5】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
方法总结 运用二次函数的性质解决生活和实际生产中的最大值和最小值问题是最常见的题目类型,解决这类问题的方法是:
1.列出二次函数的关系式,列关系式时,要根据自变量的实际意义,确定自变量的取值范围.
2.在自变量取值范围内,运用公式法或配方法求出二次函数的最大值和最小值.
举一反三 大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元).
(1)直接写出y与x之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制销售价格?
考点六、二次函数的面积问题
【例6】如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
方法总结 对于此类二次函数题型考查了待定系数法求二次函数、一次函数的解析式,二次函数的性质以及三角形面积、线段长度问题,解题的关键是运用方程思想与数形结合思想.其次就是应用到二次函数常见的水平宽铅垂高.
举一反三 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.
考点七、二次函数的综合应用
【例7】如图抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.
(1)求该二次函数的解析式;
(2)求△ACD的面积;
(3)若点Q在抛物线的对称轴上,抛物线上是否存在点P,使得以A、B、Q、P四点为顶点的四边形为平行四边形?若存在,求出满足条件的点P的坐标;若不存在,请说明理由.
方法总结 此类题型主要考查二次函数与其他知识点的综合应用,利用待定系数法求函数解析式,利用勾股定理、勾股定理的逆定理求三角形的形状;利用平行四边形的性质:对角线互相平分,对边相等是求出题中P点的关键.所以对于考查二次函数与三角形、四边形、圆、相似等相关知识的结合性题目时一定要把握好它们的性质及其常考定理与推理的综合应用.
举一反三 在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
一、 选择题
1.已知抛物线与x轴交于点A,B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线的条数是( )
A.2 B.3 C.4 D.5
2.已知下列命题:
①对于不为零的实数c,关于x的方程的根是c;
②在反比例函数中,如果函数值y<1时,那么自变量x>2;
③二次函数 的顶点在x轴下方;
④函数y= kx2+(3k+2)x+1,对于任意负实数k,当x
3时,抛物线顶点在第三象限;④若k<0,则当x<-1时,y随着x的增大而增大. 其中正确的序号是 .
4.在平面直角坐标系中,点M是直线y=3与x轴之间的一个动点,且点M是抛物线y=x2+bx+c的顶点,则方程x2+bx+c=2的解的个数是 .
5.若m、n(m<n)是关于x的方程(x﹣a)(x﹣b)+2=0的两根,且a<b,则a,b,m,n的大小关系用“<”连接的结果是
6.设二次函数y=ax2+bx+c(a≠0)的图象经过点(3,0),(7,﹣8),当3≤x≤7时,y随x的增大而减小,则实数a的取值范围是 .
7.已知抛物线与x轴交于点A,B,与y轴交于点C.若△ABC为等腰三角形,则k的值为 .
8.如图,将二次函数y=x2﹣m(其中m>0)的图象在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,形成新的图象记为y1,另有一次函数y=x+b的图象记为y2,则以下说法:
(1)当m=1,且y1与y2恰好有三个交点时,b有唯一值为1;
(2)当b=2,且y1与y2恰有两个交点时,m>4或0<m<;
(3)当m=b时,y1与y2至少有2个交点,且其中一个为(0,m);
(4)当m=﹣b时,y1与y2一定有交点.
其中正确说法的序号为 .
9.如图,抛物线y=a(x﹣1)2+(a≠0)经过y轴正半轴上的点A,点B,C分别是此抛物线和x轴上的动点,点D在OB上,且AD平分△ABO的面积,过D作DF∥BC交x轴于F点,则DF的最小值为 .
三、解答题
1.当k分别取0,1时,函数y=(1﹣k)x2﹣4x+5﹣k都有最小值吗?写出你的判断,并说明理由.
2.设函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时的函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
3.己知常数a(a是常数)满足下面两个条件:
①二次函数y1=﹣(x+4)(x﹣5a﹣7)的图象与x轴的两个交点于坐标原点的两侧;
②一次函数y2=ax+2的图象在一、二、四象限;
(1)求整数a的值;
(2)在所给直角坐标系中分别画出y1、y2的图象,并求当y1<y2时,自变量x的取值范围.
4.复习课中,教师给出关于x的函数.
教师:请独立思考,并把探索发现的与该函数有关的结论(性质)写道黑板上.
学生思考后,黑板上出现了一些结论,教师作为活动医院,又补充一些结论,并从中选择如下四条:
①存在函数,其图像经过(1,0)点;
②函数图像与坐标轴总有三个不同的交点;
③当时,不是y随x的增大而增大就是y随x的增大而减小;
④若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数。
教师:请你分别判断四条结论的真假,并给出理由.最后简单写出解决问题时所用的数学方法。
5.已知函数y=(n+1)xm+mx+1﹣n(m,n为实数)
(1)当m,n取何值时,此函数是我们学过的哪一类函数?它一定与x轴有交点吗?请判断并说明理由;
(2)若它是一个二次函数,假设n>﹣1,那么:
①当x<0时,y随x的增大而减小,请判断这个命题的真假并说明理由;
②它一定经过哪个点?请说明理由.
6.已知抛物线p:y=x2﹣(k+1)x+﹣1和直线l:y=kx+k2:
(1)对下列命题判断真伪,并说明理由:
①无论k取何实数值,抛物线p总与x轴有两个不同的交点;
②无论k取何实数值,直线l与y轴的负半轴没有交点;
(2)设抛物线p与y轴交点为C,与x轴的交点为A、B,原点O不在线段AB上;直线l与x轴的交点为D,与y轴交点为C1,当OC1=OC+2且OD2=4AB2时,求出抛物线的解析式及最小值.
7.已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2=x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
8.已知抛物线y=ax2+bx+c的顶点坐标为P(2,4).
(1)试写出b,c之间的关系式;
(2)当a>0时,若一次函数y=x+4的图象与y轴及该抛物线的交点依次为D,E,F,且E,F的横坐标x1与x2之间满足关系x2=6x1.
①求△ODE与△OEF的面积比;
②是否存在a,使得∠EPF=90°?若存在,求出a的值;若不存在,请说明理由.
9.已知二次函数h=x2﹣(2m﹣1)x+m2﹣m(m是常数,且m≠0)
(1)证明:不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)若A(n﹣3,n2+2)、B(﹣n+1,n2+2)是该二次函数图象上的两个不同点,求二次函数解析式和m的值;
(3)设二次函数h=x2﹣(2m﹣1)x+m2﹣m与x轴两个交点的横坐标分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=2﹣,请结合函数的图象回答:当y<m时,求m的取值范围.
10.为控制H7N9病毒传播,某地关闭活禽交易,冷冻鸡肉销量上升. 某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇.已知冷冻鸡肉在城市销售平均每箱的利润 y1(百元)与销售数量x(箱)的关系为,在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为:
(1)t与x的关系是 ;将y2转换为以x为自变量的函数,则y2= ;
(2)设春节期间售完冷冻鸡肉获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式;(总利润=在城市销售利润+在乡镇销售利润)
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
11.把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.
12.已知函数y1=ax2+bx,y2=ax+b(ab≠0).在同一平面直角坐标系中.
(1)若函数y1的图象过点(﹣1,0),函数y2的图象过点(1,2),求a,b的值.
(2)若函数y2的图象经过y1的顶点.
①求证:2a+b=0;
②当1<x<时,比较y1,y2的大小.
13.在平面直角坐标系中,O为坐标原点,已知二次函数y=x2+bx+c的图象过点A(0,﹣2)和点B(2,﹣2),且点C与点B关于坐标原点对称.
(1)求b,c的值,并判断点C是否在此抛物线上,并说明理由;
(2)若点P为此抛物线上一点,它关于x轴,y轴的对称点分别为M,N,问是否存在这样的P点使得M,N恰好都在直线BC上?如存在,求出点P的坐标,如不存在,并说明理由;
(3)若点P与点Q关于原点对称,当点P在位于直线BC下方的抛物线上运动时,求四边形PBQC的面积的最大值.
14.设抛物线y=(x+1)(x﹣2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.
(1)求A、B、C三点的坐标;
(2)已知点D在坐标平面内,△ABD是顶角为120°的等腰三角形,求点D的坐标;
(3)若点P、Q位于抛物线的对称轴上,且PQ=,求四边形ABQP周长的最小值.
15.如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2,C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值.
16.如图,在平面直角坐标系中,⊙O的圆心在坐标原点,半径为3.过A(﹣7,9),B(0,9)的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(1)若点D的坐标为D(3,0).
①请直接写出此时直线AD与⊙O的位置关系;
②求此时抛物线对应的函数关系式;
(2)若直线AD和⊙O相切,求抛物线二次项系数a的值;
(3)当直线AD和⊙O相交时,直接写出a的取值范围.
17.在平面直角坐标系中,现将一块含30°的直角三角板ABC放在第二象限,30°角所对的直角边AC斜靠在两坐标轴上,且点A(0,3),点C(﹣,0),如图所示,抛物线y=ax2+3ax﹣3a(a≠0)经过点B.
(1)写出点B的坐标与抛物线的解析式;
(2)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的含30°角的直角三角形?若存在,求所有点P的坐标;
(3)设过点B的直线与交x轴的负半轴于点D,交y轴的正半轴于点E,求△DOE面积的最小值.
18.如图,点P是直线:y=2x﹣2上的一点,过点P作直线m,使直线m与抛物线y=x2有两个交点,设这两个交点为A、B:
(1)如果直线m的解析式为y=x+2,直接写出A、B的坐标;
(2)如果已知P点的坐标为(2,2),点A、B满足PA=AB,试求直线m的解析式;
(3)设直线与y轴的交点为C,如果已知∠AOB=90°且∠BPC=∠OCP,求点P的坐标.
19.如图,在△ABC中,点A,B分别在x轴的正、负半轴上(其中OA<OB),点C在y轴的正半轴上,AB=10,OC=4,∠ABC=∠ACO.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点D的坐标为(﹣4,0),P是该抛物线上的一个动点.
①直线DP交直线BC于点E,当△BDE是等腰三角形时,直接写出此时点E的坐标;
②连结CD,CP,若∠PCD=∠CBD,请求出点P的坐标.
1.物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x
﹣3
﹣2
﹣1
0
1
…
y
﹣6
0
4
6
6
…
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A.2 B.3 C.4 D.5
2.要将抛物线y=x2+2x+3平移后得到抛物线y=x2,下列平移方法正确的是( )
A.向左平移1个单位,再向上平移2个单位
B.向左平移1个单位,再向下平移2个单位
C.向右平移1个单位,再向上平移2个单位
D.向右平移1个单位,再向下平移2个单位
3.已知两点均在抛物线y=ax2+bx+c上,点是该抛物线的顶点,若,则的取值范围是( )
A. B. C. D.
4.二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有( D )
A.①②③ B.②④ C.②⑤ D.②③⑤
5.二次函数y=x2+bx+c与直线y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>1时,x<1;④当x2+bx+c>时,x>;⑤当1<x<3时,x2+(b﹣1)x+c<0.
其中正确结论的编号是 .
6.已知函数的图象如图所示,观察图象,则当函数值y≤8时,对应的自变量x的取值范围是 .
7.函数y=kx+3﹣3k必过定点 ,若其与函数的交点恰好有2个,则k的值为 .
8.已知函数,若使y=k成立的x值恰好有四个,则k的取值范围为 .
9.在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=,则称点Q为点P的“可控变点”.
例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).
(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M的坐标为 .
(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16<y′≤16,则实数a的取值范围是 .
10.某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式:
y=.
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本)
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?
11.小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+3x﹣2的“旋转函数”.
小明是这样思考的:由函数y=﹣x2+3x﹣2可知,a1=﹣1,b1=3,c1=﹣2,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)写出函数y=﹣x2+3x﹣2的“旋转函数”;
(2)若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”,求(m+n)2015的值;
(3)已知函数y=﹣(x+1)(x﹣4)的图象与x轴交于点A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数y=﹣(x+1)(x﹣4)互为“旋转函数.”
12.如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).
(1)求经过A、B、C三点的抛物线解析式;
(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;
(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F,为顶点的三角形与△ABC相似吗?
13.已知函数y= (m为常数)。
(1)求证:不论m为何值,该函数的图像与x轴总有交点;
(2)当m为何值时,函数图像过原点,并指出此时函数图像与x轴的另一个交点;
(3)在(2)的情况下,怎样平移使得顶点落在x轴上,直接写出平移前后图象、对称轴和y轴围成的图形的面积。
14.已知关于x的函数(k是常数),设k分别取0,1,2时,所对应的函数为、、,某学习小组通过画图、探索,得到以下结论:
①满足>的x取值范围是-1<x<1;
②当k≥1时,在直线的左侧,必有函数图象y随x的增大而减小;
③函数与的图象的关于点(0, 1)中心对称;
④若与的图象交于A,B两点,存在整数k,函数图象与y轴交于点C,满足△ABC为直角三角形.
请你判断结论的真假,并说明理由.最后简单写出解决问题时所用的数学方法.
15.如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
16.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
答案
【例1】 1.A
2. 3
解:∵x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,
∴二次函数y=x2+4x+6的对称轴为直线x==,
又∵二次函数y=x2+4x+6的对称轴为直线x=﹣2,
∴=﹣2,
∴3m+3n+2=﹣4,m+n=﹣2,
∴当x=3(m+n+1)=3(﹣2+1)=﹣3时,
x2+4x+6=(﹣3)2+4×(﹣3)+6=3.
3.D
解:y=ax2﹣2ax+1(a<0),
对称轴是直线x=﹣=1,
即二次函数的开口向下,对称轴是直线x=1,
即在对称轴的右侧y随x的增大而减小,
A点关于直线x=1的对称点是D(3,y1),
∵2<3<4,
∴y2>y1>y3,
举一反三 1.D
解:∵点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,
∴(a﹣2b)2+4×(a﹣2b)+10=2﹣4ab,
a2﹣4ab+4b2+4a﹣8b+10=2﹣4ab,
(a+2)2+4(b﹣1)2=0,
∴a+2=0,b﹣1=0,
解得a=﹣2,b=1,
∴a﹣2b=﹣2﹣2×1=﹣4,
2﹣4ab=2﹣4×(﹣2)×1=10,
∴点A的坐标为(﹣4,10),
∵对称轴为直线x=﹣=﹣2,
∴点A关于对称轴的对称点的坐标为(0,10).
2.
解:根据题意,得
①该函数是一次函数,即2m﹣1=0,
解,得m=;
②该函数和x轴有一个交点,即△=9﹣4m(2m﹣1)=﹣8m2+4m+9=0,
解,得m=;
③该函数是二次函数,与y轴的交点是原点,与x轴有2个交点,即m=0.
故答案为.
3. B
【例2】 ①③④
解:∵抛物线开口向下,
∴a<0,
∴2a<0,
对称轴x=﹣>1,﹣b<2a,
∴2a+b>0,故选项①正确;
令ax2+bx+c=0,抛物线与轴交于(x1,0),(x2,0)则x1•x2=,
由图不能准确判断与1大小,则无法确定a,c的大小关系,故选项②不正确
∵﹣1<m<n<1,则﹣2<m+n<2,
∴抛物线对称轴为:x=﹣>1,>2,m+n,故选项③正确;
当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,
∴3a+c>﹣2b,∴﹣3a﹣c<2b,
∵a<0,b>0,c<0(图象与y轴交于负半轴),
∴3|a|+|c|=﹣3a﹣c<2b=2|b|,故④选项正确.
故答案为:①③④.
举一反三 1. ①②④
解:①∵抛物线与x轴由两个交点,
∴b2﹣4ac>0,
①正确;
②由图象可知,当x=﹣2时,y>0,
即4a﹣2b+c>0,
∴4a+c>2b,
②正确;
③∵x=﹣1时,y>0,
∴a﹣b+c>0,
∴a+c>b,
∵a+b+c<0,∴a+c<﹣b,
∴(a+c)2<b2,
③错误;
④∵x=﹣1时,y有最大值a﹣b+c,
∴ax2+bx+c≤a﹣b+c,
∴x(ax+b)≤a﹣b,
④正确.
故答案为:①②④.
2.C
解:∵根据图示知,一次函数与二次函数的交点A的坐标为(﹣2,0),
∴﹣2a+b=0,
∴b=2a.
∵由图示知,抛物线开口向上,则a>0,
∴b>0.
∵反比例函数图象经过第一、三象限,
∴k>0.
A、由图示知,双曲线位于第一、三象限,则k>0,
∴2a+k>2a,即b<2a+k.
故A选项错误;
B、∵k>0,b=2a,
∴b+k>b,
即b+k>2a,
∴a=b+k不成立.
故B选项错误;
C、∵a>0,b=2a,
∴b>a>0.
故C选项错误;
D、观察二次函数y=ax2+bx和反比例函数y=(k≠0)图象知,当x=﹣=﹣=﹣1时,y=﹣k>﹣=﹣=﹣a,即k<a,
∵a>0,k>0,
∴a>k>0.
故D选项正确;
故选:D.
【例3】C
解:首先将二次函数的解析式配方化为顶点式,然后确定如何平移,即y=-2x2+4x+1=-2(x-1)2+3,将该函数图象向左平移1个单位,再向下平移3个单位就得到y=-2x2的图象.
举一反三 A
【例4】
解:(1)由抛物线的对称性可知AE=BE.
∴△AOD≌△BEC.
∴OA=EB=EA.
设菱形的边长为2m,在Rt△AOD中,
m2+()2=(2m)2,解得m=1.
∴DC=2,OA=1,OB=3.
∴A,B,C三点的坐标分别为(1,0),(3,0),(2,).
(2)解法一:设抛物线的解析式为y=a(x-2)2+,代入A的坐标(1,0),得a=-.
∴抛物线的解析式为y=-(x-2)2+.
解法二:设这个抛物线的解析式为y=ax2+bx+c,由已知抛物线经过A(1,0),B(3,0),C(2,)三点,
得解这个方程组,得
∴抛物线的解析式为y=-x2+4x-3.
举一反三 y=x2﹣2x﹣3
解:∵y=x2+2x+1=(x+1)2,
∴A点坐标为(﹣1,0),
解方程组得或,
∴点C′的坐标为(1,4),
∵点C和点C′关于x轴对称,
∴C(1,﹣4),
设原抛物线解析式为y=a(x﹣1)2﹣4,
把A(﹣1,0)代入得4a﹣4=0,解得a=1,
∴原抛物线解析式为y=(x﹣1)2﹣4=x2﹣2x﹣3.
故答案为y=x2﹣2x﹣3.
【例5】
解:(1)当1≤x<50时,y=(200﹣2x)(x+40﹣30)=﹣2x2+180x+2000,
当50≤x≤90时,
y=(200﹣2x)(90﹣30)=﹣120x+12000,
综上所述:y=;
(2)当1≤x<50时,二次函数开口向下,二次函数对称轴为x=45,
当x=45时,y最大=﹣2×452+180×45+2000=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)当1≤x<50时,y=﹣2x2+180x+2000≥4800,解得20≤x≤70,
因此利润不低于4800元的天数是20≤x<50,共30天;
当50≤x≤90时,y=﹣120x+12000≥4800,解得x≤60,
因此利润不低于4800元的天数是50≤x≤60,共11天,
所以该商品在销售过程中,共41天每天销售利润不低于4800元.
举一反三
解:(1)由题意可得:y=;
(2)由题意可得:w=,
化简得:w=,
即w=,
由题意可知x应取整数,故当x=﹣2或x=﹣3时,w<6125<6250,
故当销售价格为65元时,利润最大,最大利润为6250元;
(3)由题意w≥6000,如图,令w=6000,
将w=6000带入﹣20≤x<0时对应的抛物线方程,即6000=﹣20(x+)2+6125,
解得:x1=﹣5,
将w=6000带入0≤x≤30时对应的抛物线方程,即6000=﹣10(x﹣5)2+6250,
解得x2=0,x3=10,
综上可得,﹣5≤x≤10,
故将销售价格控制在55元到70元之间(含55元和70元)才能使每月利润不少于6000元.
【例6】
解:(1)∵对称轴为直线x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,
∴A、B两点关于直线x=﹣1对称,
∵点A的坐标为(﹣3,0),
∴点B的坐标为(1,0);
(2)①a=1时,∵抛物线y=x2+bx+c的对称轴为直线x=﹣1,
∴=﹣1,解得b=2.
将B(1,0)代入y=x2+2x+c,
得1+2+c=0,解得c=﹣3.
则二次函数的解析式为y=x2+2x﹣3,
∴抛物线与y轴的交点C的坐标为(0,﹣3),OC=3.
设P点坐标为(x,x2+2x﹣3),
∵S△POC=4S△BOC,
∴×3×|x|=4××3×1,
∴|x|=4,x=±4.
当x=4时,x2+2x﹣3=16+8﹣3=21;
当x=﹣4时,x2+2x﹣3=16﹣8﹣3=5.
∴点P的坐标为(4,21)或(﹣4,5);
②设直线AC的解析式为y=kx+t (k≠0)将A(﹣3,0),C(0,﹣3)代入,
得,解得,
即直线AC的解析式为y=﹣x﹣3.
设Q点坐标为(x,﹣x﹣3)(﹣3≤x≤0),则D点坐标为(x,x2+2x﹣3),
QD=(﹣x﹣3)﹣(x2+2x﹣3)=﹣x2﹣3x=﹣(x+)2+,
∴当x=﹣时,QD有最大值.
举一反三
解:(1)y=mx2﹣2mx﹣3m=m(x﹣3)(x+1),
∵m≠0,
∴当y=0时,x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0);
(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:,
解得,
故C1:y=x2﹣x﹣.
如图:过点P作PQ∥y轴,交BC于Q,
由B、C的坐标可得直线BC的解析式为:y=x﹣,
设P(x,x2﹣x﹣),则Q(x,x﹣),
PQ=x﹣﹣(x2﹣x﹣)=﹣x2+x,
S△PBC=PQ•OB=×(﹣x2+x)×3=﹣(x﹣)2+,
当x=时,S△PBC有最大值,Smax=,
×()2﹣﹣=﹣,
P(,﹣);
(3)y=mx2﹣2mx﹣3m=m(x﹣1)2﹣4m,
顶点M坐标(1,﹣4m),
当x=0时,y=﹣3m,
∴D(0,﹣3m),B(3,0),
∴DM2=(0﹣1)2+(﹣3m+4m)2=m2+1,
MB2=(3﹣1)2+(0+4m)2=16m2+4,
BD2=(3﹣0)2+(0+3m)2=9m2+9,
当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.
①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,
解得m=﹣1(∵m<0,∴m=1舍去);
②DM2+MB2=BD2时有:m2+1+16m2+4=19m2+9,
解得m=﹣(m=舍去).
综上,m=﹣1或﹣时,△BDM为直角三角形.
【例7】
解:(1)当x=0时,y=3,即C(0,3)
将A、C、B点坐标代入、及对称轴,得
,
解得,
抛物线的解析式y=﹣x2﹣2x+3;
(2)∵y=﹣x2﹣2x+3=﹣(x﹣1)2+4,得顶点坐标是(﹣1,4),
由勾股定理,得
AC2=32+(0﹣3)2=18,
CD2=(0+1)2+(3﹣4)2=2,
AD2=(﹣1+3)2+((4﹣0)2=20,
AC2+CD2=AD2,
∴△ACD是直角三角形,
S△ACD=AC•CD=××=3;
(3)①如图1,
平行四边形AQBP,由对角线互相平分,得P1(﹣1,4),Q(﹣1,﹣4);
②如图2,
▱ABQP,PQ=AB=4,﹣1﹣4=﹣5,
当x=﹣5时,y=﹣25+10+3=﹣12,即P2(﹣5,﹣12);
③如图3,
▱ABPQ,PQ=AB=4,P点的横坐标为﹣1+4=3,
当x=3时,y=﹣9﹣6+3=﹣12,即P3(3,﹣12),
综上所述:P1(﹣1,4),P2(﹣5,﹣12),P3(3,﹣12).
举一反三
解:(1)设此抛物线的函数解析式为:
y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:
解得,
所以此函数解析式为:y=;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,),
∴S=S△AOM+S△OBM﹣S△AOB
=×4×(﹣m2﹣m+4)+×4×(﹣m)﹣×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时S有最大值S=4.
(3)设P(x,x2+x﹣4).
当OB为边时,根据平行四边形的性质知PQ∥OB,且PQ=OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣(x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(﹣4,4)或(﹣2+2,2﹣2)或(﹣2﹣2,2+2)或(4,﹣4).
一、选择题
1.C
解:y=k(x+1)(x﹣)=(x+1)(kx﹣3),
所以,抛物线经过点A(﹣1,0),C(0,﹣3),
AC===,
点B坐标为(,0),
①k>0时,点B在x正半轴上,
若AC=BC,则=,解得k=3,
若AC=AB,则+1=,解得k==,
若AB=BC,则+1=,解得k=;
②k<0时,点B在x轴的负半轴,点B只能在点A的左侧,
只有AC=AB,则﹣1﹣=,解得k=﹣=﹣,
所以,能使△ABC为等腰三角形的抛物线共有4条.
2. B
解:对于不为零的实数c,关于x的方程x+=c+1的根是c和1,所以①错误;
在反比例函数y=中,如果函数值y<1时,那么自变量x>2或x<0,所以②错误;
二次函数y=x2﹣2mx+2m﹣2,△=4m2﹣4(2m﹣2)=4(m﹣1)2+4>0,则抛物线与x轴有两个交点,而抛物线开口向上,所以抛物线的顶点在x轴下方,所以③正确;
函数y=kx2+(3k+2)x+1,则抛物线的对称轴为直线x=﹣=﹣﹣,而当x<m时,y随x的增大而增大,所以m≤﹣﹣,当﹣<k<0,m的没有最大整数,所以④错误.
故选B.
3.A
解:易求x=1时,三个函数的函数值都是1,
所以,交点坐标为(1,1),
根据对称性,y=x和y=在第三象限的交点坐标为(﹣1,﹣1),
①如果,那么0<a<1,故①正确;
②如果,那么a>1或﹣1<a<0,故②错误;
③如果,那么a值不存在,故③错误;
④如果时,那么a<﹣1,故④正确.
综上所述,正确的命题是①④,错误的命题是②③.
故选:A.
4. B
解:∵一次函数y2=dx+e(d≠0)的图象经过点(x1,0),
∴dx1+e=0,
∴y2=d(x﹣x1),
∴y=y1+y2=a(x﹣x1)(x﹣x2)+d(x﹣x1)
=(x﹣x1)[a(x﹣x2)+d]
∵函数y=y1+y2的图象与x轴仅有一个交点,
∴函数y=y1+y2是二次函数,且它的顶点在x轴上,
即y=y1+y2=a,
∴a(x﹣x2)+d=a(x﹣x1),
令x=x2,可得
a(x2﹣x2)+d=a(x2﹣x1),
∴a(x2﹣x1)=d.
故选:B.
5.C
解:∵二次函数y=ax2+bx+c(a,b,c为常数,且a<0)的图象经过点(﹣1,1),(4,﹣4),
∴a﹣b+c=1①,
16a+4b+c=﹣4②,
②﹣①,得15a+5b=﹣5,即3a+b=﹣1,
∴b=﹣1﹣3a,
∴c=1﹣a+b=1﹣a﹣1﹣3a=﹣4a.
(1)∵c=﹣4a,
∴==﹣<0,故结论正确;
(2)∵y=ax2+bx+c=ax2+(﹣1﹣3a)x﹣4a,
∴对称轴为直线x==+,
∵a<0,
∴x=+<,
∴当x>+时,y的值随x值的增大而减小,故结论错误;
(3)∵16a+4b+c=﹣4,
∴16a+4(b+1)+c=0,
∴x=4是方程ax2+(b+1)x+c=0的一个根,故结论正确;
(4)∵a﹣b+c=1,
∴a﹣(b+1)+c=0,
∴x=﹣1是方程ax2+(b+1)x+c=0的一个根,
由(3)知x=4是方程ax2+(b+1)x+c=0的一个根,
∴(﹣1,0),(4,0)是二次函数y=ax2+(b+1)x+c与x轴的两个交点,
又∵a<0,
∴当﹣1<x<4时,y>0,即ax2+(b+1)x+c>0,故结论正确.
所以正确的结论是(1)(3)(4).
故选C.
6.A
解:∵a<0,
∴抛物线开口向下,
∵图象经过(0,5)、(10,8)两点,0<h<10,
∴对称轴在5到10之间,
∴h的值可能是7.
故选A.
7.C
解:∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,所以①正确;
∵抛物线的顶点为D(﹣1,3),
∴a﹣b+c=3,
∵抛物线的对称轴为直线x=﹣=﹣1,
∴b=2a,
∴a﹣2a+c=3,即c﹣a=3,所以②正确;
∵抛物线的对称轴为直线x=﹣1,
∵抛物线与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以③正确;
∵抛物线的顶点为D(﹣1,3),
∵当x=﹣1时,二次函数有最大值为3,
∴方程ax2+bx+c=3有两个相等的实数根,
∵m≥2,
∴方程ax2+bx+c=m(m>3)没有实数根,所以④错误.
故选:C.
二、填空题
1. ﹣1 ; 增大
2. 8 , -1
3. ①③
解:函数y=k(x+1)(x﹣)的图象与x轴交于(﹣1,0)(,0),
①方程k(x+1)(x﹣)=﹣3,
解得:x1=0,x2=﹣1,
∴①正确;
②∵函数y=k(x+1)(x﹣)的图象与x轴交于(﹣1,0),(,0),
∴移动函数图象使其经过原点,则将图象向右移动1个单位或移动﹣单位,
∴②错误,
③当k>3时,<1,
∴对称轴在y轴的左侧,开口向上,与x轴有两个交点,
∴③正确,
④若k<0,开口向下,在对称轴的左侧,y随着x的增大而增大,
∵函数y=k(x+1)(x﹣)的对称轴方程是:x=<0,
∴④错误.
4. 0,1或2
解:分三种情况:
点M的纵坐标小于2,方程x2+bx+c=2的解是2个不相等的实数根;
点M的纵坐标等于2,方程x2+bx+c=2的解是2个相等的实数根;
点M的纵坐标大于2,方程x2+bx+c=2的解的个数是0.
故方程x2+bx+c=2的解的个数是0,1或2.
故答案为:0,1或2.
5. a<m<n<b
解:∵(x﹣a)(x﹣b)+2=0,
∴(x﹣a)(x﹣b)=﹣2,
∴m、n可看作抛物线y=(x﹣a)(x﹣b)与直线y=﹣2的两交点的横坐标,
∵抛物线y=(x﹣a)(x﹣b)与x轴的两交点坐标为(a,0),(b,0),如图,
∴a<m<n<b.
故答案为:a<m<n<b.
6. ﹣≤a<0或0<a≤
解:把(3,0),(7,﹣8)代入解析式得,
,
②﹣①得,b=﹣2﹣10a,
抛物线的对称轴为直线x=﹣=+5,
当a>0时,+5≥7,y随x的增大而减小,即0<a≤,
当a<0时,+5≤3,y随x的增大而减小,即﹣≤a<0,
故答案为:﹣≤a<0或0<a≤.
7.,,,2
解:化为一般式,得
y=kx2+(﹣2+k)x﹣2,
当y=0时,kx2+(﹣2+k)x﹣2=0,
解得x=﹣1,x=,即A(﹣1,0),B(,0),
当x=0时,y=﹣2,即C(0,﹣2).
当AB=BC时,=+1,化简,得=3,解得k=
当AB=AC时,±=+1,化简,解得k=或k=;
当AC=BC时,=,化简,得=﹣1,或=﹣1,解得k=﹣2(不符合题意要舍去),或k=2,
故答案为:,,,2.
8.(2),(3)
解:(1)当m=1,且y1与y2恰好有三个交点时,b有唯一值为1,b=故(1)错误;
(2)当b=2,且y1与y2恰有两个交点时,m>4或0<m<,故(2)正确;
(3)当m=b时,y1与y2至少有2个交点,且其中一个为(0,m)故(3)正确;
(4)当m=﹣b时,y1与y2没有交点,故(4)错误;
故答案为:(2),(3).
9.
解:设点B的坐标为(m,a(m﹣1)2+),点C坐标为(n,0).
∵点D在OB上,且AD平分△ABO的面积,
∴OD=BD,
又∵DF∥BC,
∴DF是△OBC的中位线,
∴DF=BC.
根据两点间的距离公式可知:
BC2=(m﹣n)2+=(m﹣n)2+a2(m﹣1)4+2a(m﹣1)2+2,
结合抛物线开口向上可知a>0,
∴(m﹣n)2≥0,a2(m﹣1)4≥0,2a(m﹣1)2≥0,
∴BC2≥2,
∴BC=.
∵DF=BC,
∴DF≥.
故答案为:.
三、解答题
1.解:当k=0时,y=x2﹣4x+5=(x﹣2)2+1,
所以当k=0时,函数有最小值1;
当k=1时,y=﹣4x+4,
所以无最小值.
2.
解:(1)当k=0时,y=﹣(x﹣1)(x+3),所画函数图象如图所示:
(2)①根据图象知,图象都经过点(1,0)和(﹣1,4).
②图象与x轴的交点是(1,0).
③k取0和2时的函数图象关于点(0,2)中心对称.
④函数y=(x﹣1)[(k﹣1)x+(k﹣3)](k是常数)的图象都经过(1,0)和(﹣1,4)等等.
(3)平移后的函数y2的表达式为y2=(x+3)2﹣2.
所以当x=﹣3时,函数y2的最小值是﹣2.
3.
解:(1)抛物线y1=﹣(x+4)(x﹣5a﹣7)的图象与x轴的两个交点坐标为(﹣4,0),(5a+7,0),
根据题意得5a+7>0,解得a>﹣,
又因为一次函数y2=ax+2的图象在一、二、四象限,则a<0,
所以a的范围为﹣<a<0,
所以整数a为﹣1;
(2)抛物线解析式为y1=﹣(x+4)(x﹣2)=﹣(x+1)2+3,抛物线的顶点坐标为(﹣1,3),
直线解析式为y=﹣x+2,
如图,
当x<﹣1或x>2时,y1<y2.
4.
解:①真;将(1,0)代入可得:2k﹣(4k+1)﹣k+1=0,
解得:k=0.
运用方程思想;
②假;反例:k=0时,只有两个交点.运用举反例的方法;
③假;如k=1,﹣=,当x>1时,先减后增;运用举反例的方法;
④真;当k=0时,函数无最大、最小值;
k≠0时,y最==﹣,
∴当k>0时,有最小值,最小值为负;
当k<0时,有最大值,最大值为正.运用分类讨论思想.
5.
解:(1)①当m=1,n≠﹣2时,函数y=(n+1)xm+mx+1﹣n(m,n为实数)是一次函数,它一定与x轴有一个交点,
∵当y=0时,(n+1)xm+mx+1﹣n=0,∴x=,
∴函数y=(n+1)xm+mx+1﹣n(m,n为实数)与x轴有交点;
②当m=2,n≠﹣1时,函数y=(n+1)xm+mx+1﹣n(m,n为实数)是二次函数,
当y=0时,y=(n+1)xm+mx+1﹣n=0,
即:(n+1)x2+2x+1﹣n=0,
△=22﹣4(1+n)(1﹣n)=4n2≥0;
∴函数y=(n+1)xm+mx+1﹣n(m,n为实数)与x轴有交点;
③当n=﹣1,m≠0时,函数y=(n+1)xm+mx+1﹣n是一次函数,当y=0时,x=,
∴函数y=(n+1)xm+mx+1﹣n(m,n为实数)与x轴有交点;
(2)①假命题,若它是一个二次函数,
则m=2,函数y=(n+1)x2+2x+1﹣n,
∵n>﹣1,∴n+1>0,
抛物线开口向上,
对称轴:﹣==﹣<0,
∴对称轴在y轴左侧,当x<0时,y有可能随x的增大而增大,也可能随x的增大而减小,
②当x=1时,y=n+1+2+1﹣n=4.
当x=﹣1时,y=0.
∴它一定经过点(1,4)和(﹣1,0).
6.
解:(1)①正确,
∵x2﹣(k+1)x+﹣1=0的解是抛物线与x轴的交点横坐标,
由判别式△=(k+1)2﹣4(﹣1)=k2﹣4k+5=(k﹣2)2+1>0,
∴无论k取何实数值,抛物线总与x轴有两个不同的交点;
②正确.
∵直线y=kx+k2,与y轴交点坐标是(0,k2),而无论k取何实数值k2≥0,
∴直线与y轴的负半轴没有交点.
(2)∵|OD|=|﹣k|,|AB|=
∴OD2=4AB2,
即k2=4k2﹣16k+20,
解得,k=2或k=
又∵OC1=k2,OC=﹣1>0,
∴k2=﹣1+2,
解得k=2或k=﹣,
综上得k=2,
∴抛物线解析式为y=x2﹣3x+2,最小值为﹣.
7.解:根据OC长为8可得一次函数中的n的值为8或﹣8.
分类讨论:①n=8时,易得A(﹣6,0)如图1,
∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a<0,
∵AB=16,且A(﹣6,0),
∴B(10,0),而A、B关于对称轴对称,
∴对称轴直线x==2,
要使y1随着x的增大而减小,且a<0,
∴x≥2;
②n=﹣8时,易得A(6,0),如图2,
∵抛物线过A、C两点,且与x轴交点A,B在对称轴两侧,
∴抛物线开口向上,则a>0,
∵AB=16,且A(6,0),
∴B(﹣10,0),而A、B关于对称轴对称,
∴对称轴直线x==﹣2,
要使y1随着x的增大而减小,且a>0,
∴x≤﹣2.
综上所述,x≥2或x≤﹣2.
8.
解:(1)∵抛物线顶点坐标为(2,4),
∴抛物线解析式为y=a(x﹣2)2+4=ax2﹣4ax+4a+4,
∴b=﹣4a,c=4a+4,
∴b+c=4;
(2)①由题意可知△ODE和△ODF的底边DE、DF边上的高相同,
∴S△ODE:S△ODF=DE:DF=x1:x2=1:6,
∴S△ODE:S△OEF=1:5;
②如图,分别过E、F作x轴的垂线,垂足分别为G、H,交直线DP于点M、N,
∵直线y=x+4,
∴设点E坐标为(m,m+4),则点F的坐标为(6m,6m+4),
∴EM=EG﹣MG=m+4﹣4=m,FN=FH﹣NH=6m+4﹣4=6m,PM=PD﹣MD=2﹣m,PN=DN﹣PD=6m﹣2,
∵∠EPF=90°,
∴∠EPM+∠FPN=90°,且∠FPN+∠PFN=90°,
∴∠EPM=∠PFN,
∴△EPM∽△PEN,
∴=,即=,
整理可得6m2+7m+2=0,解得m=或m=,
当m=时,点E(,),F(3,7),把F点坐标代入抛物线解析式可得a+4=7,解得a=3,
∴抛物线解析式为y=3(x﹣2)2+4,当x=时,代入可求得y=≠,即点E不在该抛物线图象上,不符合题意,
当m=时,点E(,4),F(4,8),把F点坐标代入抛物线解析式可求得a=1,
∴抛物线解析式为y=(x﹣2)2+4,当x=时,代入可求得y=≠4,即点E不在抛物线图象上,不符合题意,
综上可知不存在满足条件的a的值.
9.
解:(1)由题意有△=[﹣(2m﹣1)]2﹣4(m2﹣m)=1>0.
即不论m取何值时,该二次函数图象总与x轴有两个交点;
(2)∵A(n﹣3,n2+2)、B(﹣n+1,n2+2)是该二次函数图象上的两个不同点,
∴抛物线的对称轴x==﹣1,
∴=﹣1,
∴m=﹣,
∴抛物线解析式为h=x2+2x+;
(3)令h=x2﹣(2m﹣1)x+m2﹣m=0,
解得x1=m,x2=m﹣1,
即y=2﹣=,
作出图象如右:
当=m时,
解得m=,
当y<m时,m的取值范围为m>或﹣<m<0.
10.
解:(1)∵某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,在城市销售数量x(箱),
∴在乡镇销售数量t(箱)的关系为:t=60﹣x,
∴y2=.
故答案为:t=60﹣x,;
(2)综合y1=和(1)中 y2,当对应的x范围是0<x≤20 时,
W1=(x+5)x+(x+4)(60﹣x)
=x2+5x+240;
(3)当20<x≤30 时,
W2=(﹣x+7.5)x+(x+4)(60﹣x)
=﹣x2+7.5x+240,
∵x=﹣=>30,
∴W在20<x≤30随x增大而增大,
∴最大值x=30时取得,
∴W最大=382.5(百元).
11.
解:(1)当t=3时,h=20t﹣5t2=20×3﹣5×9=15(米),
∴当t=3时,足球距离地面的高度为15米;
(2)∵h=10,
∴20t﹣5t2=10,即t2﹣4t+2=0,
解得:t=2+或t=2﹣,
故经过2+或2﹣时,足球距离地面的高度为10米;
(3)∵m≥0,由题意得t1,t2是方程20t﹣5t2=m 的两个不相等的实数根,
∴b2﹣4ac=202﹣20m>0,
∴m<20,
故m的取值范围是0≤m<20.
12.
解:(1)由题意得:,解得:,
故a=1,b=1.
(2)①证明:∵y1=ax2+bx=a,
∴函数y1的顶点为(﹣,﹣),
∵函数y2的图象经过y1的顶点,
∴﹣=a(﹣)+b,即b=﹣,
∵ab≠0,
∴﹣b=2a,
∴2a+b=0.
②∵b=﹣2a,
∴y1=ax2﹣2ax=ax(x﹣2),y2=ax﹣2a,
∴y1﹣y2=a(x﹣2)(x﹣1).
∵1<x<,
∴x﹣2<0,x﹣1>0,(x﹣2)(x﹣1)<0.
当a>0时,a(x﹣2)(x﹣1)<0,y1<y2;
当a<0时,a(x﹣1)(x﹣1)>0,y1>y2.
13.
解:(1)∵二次函数y=x2+bx+c的图象过点A(0,﹣2)和点B(2,﹣2),
∴,
解得,
∴y=x2﹣x﹣2.
∵点C与点B关于坐标原点对称,
∴C(﹣2,2),
把x=﹣2代入y=x2﹣x﹣2,得y=×(﹣2)2﹣(﹣2)﹣2=2,
∴C(﹣2,2)在此抛物线上;
(2)设直线BC的解析式为y=mx+n,
∵B(2,﹣2),C(﹣2,2),
∴,解得,
∴直线BC的解析式为y=﹣x.
假设此抛物线上存在这样的点P(x,x2﹣x﹣2),使得它关于x轴,y轴的对称点M,N恰好都在直线BC上,
∵M(x,﹣x2+x+2),N(﹣x,x2﹣x﹣2),
∴x2﹣x﹣2=x,
解得x=2±2,
故所求点P的坐标为(2+2,2+2),或(2﹣2,2﹣2);
(3)∵点C与点B关于原点对称,点P与点Q关于原点对称,
∴四边形PBQC是平行四边形,
∴S▱PBQC=2S△PBC,
∴当△PBC面积最大时,四边形PBQC的面积最大.
将直线BC向下平移t个单位得到直线y=﹣x﹣t,当它与抛物线只有一个交点时,△PBC面积最大.
把y=﹣x﹣t代入y=x2﹣x﹣2,得﹣x﹣t=x2﹣x﹣2,
整理得,x2﹣2+t=0,
△=0﹣4×(﹣2+t)=0,
解得t=2,
解方程x2﹣2+2=0,解得x=0,
则y=﹣2,即P(0,﹣2),
此时四边形PBQC的面积的最大值为:2×4=8.
14.
解:(1)当x=0时,y=﹣;
当y=0时,x=﹣1或x=2;
则A(﹣1,0),B(0,﹣),C(2,0);
(2)如图,Rt△ABO中,OA=1,OB=,
∴AB=2,∠ABO=30°,∠BAO=60°,
∴△ABD是顶角为120°的等腰三角形.
①当AB为底时,若点D在AB上方,由∠ABO=∠BAD=30°,AB=2,得D1(0,﹣),
若点D在AB下方,由∠BAD=∠DBA=30°,AB=2,得D2(﹣1,﹣),
②当AB为腰时,A为顶点时,
∵∠DAB=120°,∠OAB=60°,AD=AB=2,
∴点D在y轴或x轴上,
若D在y轴上,得D3(0,),若D在x轴上,得D4(﹣3,0);
③当AB为腰时,A为顶点时,
若点D在第三象限,
∵∠DBO=150°,BD=2,得D5(﹣1,﹣2);
若点D在第四象限时,
∵DB∥x轴,BD=2,得D6(2,﹣),
∴符合要求的点D的坐标为(0,﹣),(﹣1,﹣),(0,),(﹣3,0),(﹣1,﹣2),(2,﹣);
(3)当AP+BQ最小时,四边形ABQP的周长最小,
把点B向上平移个单位后得到B1(0,﹣),
∵BB1∥PQ,且BB1=PQ,
∴四边形BB1PQ是平行四边形,
∴BQ=B1P,
∴AP+BQ=AP+B1P,
要在直线x=上找一点P,使得AP+B1P最小,
作点B1关于直线x=的对称点,得B2(1,﹣),
则AB2就是AP+BQ的最小值,AB2==,
AB=2,PQ=,
∴四边形ABQP的周长最小值是+2.
15.
解:(1)∵抛物线C1经过原点,与X轴的另一个交点为(2,0),
∴,解得,
∴抛物线C1的解析式为y=x2﹣2x,
∴抛物线C1的顶点坐标(1,﹣1),
(2)如图1,
∵抛物线C1向右平移m(m>0)个单位得到抛物线C2,
∴C2的解析式为y=(x﹣m﹣1)2﹣1,
∴A(m,0),B(m+2,0),C(0,m2+2m),
过点C作CH⊥对称轴DE,垂足为H,
∵△ACD为等腰直角三角形,
∴AD=CD,∠ADC=90°,
∴∠CDH+∠ADE=90°
∴∠HCD=∠ADE,
∵∠DEA=90°,
∴△CHD≌△DEA,
∴AE=HD=1,CH=DE=m+1,
∴EH=HD+DE=1+m+1=m+2,
由OC=EH得m2+2m=m+2,解得m1=1,m2=﹣2(舍去),
∴抛物线C2的解析式为:y=(x﹣2)2﹣1.
(3)如图2,连接BC,BP,
由抛物线对称性可知AP=BP,
∵△PAC为等边三角形,
∴AP=BP=CP,∠APC=60°,
∴C,A,B三点在以点P为圆心,PA为半径的圆上,
∴∠CBO=∠CPA=30°,
∴BC=2OC,
∴由勾股定理得OB==OC,
∴(m2+2m)=m+2,
解得m1=,m2=﹣2(舍去),
∴m=.
16.
解:(1)①设过点A和D的直线为y=kx+b,把A和D的坐标代入得:
,
解得:,
∴y=﹣x+,
∴直线和y轴交点坐标为(0,),
∴圆心O到直线AD的距离d=≈2.1,
∵圆的半径r=3,
∴d<r,
∴此时直线AD与⊙O的位置关系为相交;
②因为抛物线过A(﹣7,9),B(0,9)D(3,0).可设抛物线解析式为y=ax2+bx+9(a≠0),
得:,
解得:,
即抛物线的解析式为:y=﹣x2﹣x+9;
(2)如图所示,过A有两条圆的切线,切点为G,连OG,过A作AH⊥x轴.
∵∠OGD=∠AHD=90°,∠ADH=∠ADH,
∴△OGD∽△AHD,
∴OG:OD=AH:AD,
∵OG=3,AH=9,OD=|m|,
∴AD=3|m|,
在Rt△AHD中,92+(m+7)2=(3m)2,
得:4m2﹣7m﹣65=0,
∴,
∴OD=5或,
∴点D的坐标为(5,0)或(﹣,0),
设抛物线解析式为=ax2+bx+9,把A和D的坐标分别代入可得;
(3)由(2)可知当直线AD和⊙O相切时,a的值为﹣或,
所以当直线AD和⊙O相交时,a的取值范围为:.
17.
解:(1)过点B作BD⊥x轴,垂足为D,
∵点A(0,3),点C(﹣,0),
∴OA=3,OC=,
在直角三角形AOC中,AC=2,
∵在直角三角形ABC中,∠ABC=30°,
∴BC=tan60°×AC=×2=6,
∵∠BCD+∠ACO=90°,∠ACO+∠CAO=90°,
∴∠BCD=∠CAO,
又∵∠BDC=∠COA=90°,
∴△BCD∽△CAO,
∴=,
∴BD=×=3,
∴AB∥x轴
在直角三角形BDC中,根据勾股定理求得:
DC=3,
∴OD=OC+DC=+3=4,
∴点B的坐标为(﹣4,3);
把点B的坐标为(﹣4,3)代入y=ax2+3ax﹣3a(a≠0)
解得:a=,
∴抛物线的解析式为:y=x2+x﹣1.
设直线BC的解析式为:y=kx+b,把B(﹣4,3),C(﹣,0)代入得;
k=﹣,b=﹣1,
∴直线BC的解析式为y=﹣x﹣1,
(2)假设存在点P,使得△ACP仍然是以AC为直角边的含30°角的直角三角形:
①若以点C为直角顶点;
则延长BC至点P1,使得P1C=BC,得到直角三角形△ACP1,
过点P1作P1M⊥x轴,
∵CP1=BC,∠MCP1=∠BCD,∠P1MC=∠BDC=90°,
∴△MP1C≌△DBC.
∴CM=CD=3,P1M=BD=3,可求得点P1(2,﹣3);
②若以点A为直角顶点;
则过点A作AP2⊥CA,且使得AP2=BC,得到直角三角形△ACP2,
过点P2作P2N⊥y轴,同理可证△AP2N≌△CBD,
∴NP2=DC=3,AN=BD=3,可求得点P2(3,0),
③延长BC交y轴于P3构成Rt△ACP3,
∵AB∥x轴,
∴∠CAP3=30°,
∴Rt△ACP3是含有30°角的直角三角形,
∴与y轴的交点为P3(0,﹣1)
经检验,点P1(2,﹣3)与点P2(3,0)都不在抛物线y=x2+x﹣1上,P3在抛物线y=x2+x﹣1上
∴在抛物线上存在点P(点B除外),使△ACP仍然是以AC为直角边的含30°角的直角三角形.
(3)设E点的坐标为(0,b),
∴直线DE的解析式为y=kx+b,
∵B点的坐标(﹣4,3),代入得3=﹣4k+b,
∴k=,
∴直线DE的解析式为y=x+b,
∴D点的坐标为(﹣,0)
∴S△DOE=OD×OE=××b==2×=2×=2[(b﹣3)+]+12
∴当b﹣3=时,即b=6,S△DOE有最小值,
∴△DOE面积的最小值为24.
18.
解:(1)∵直线m解析式为:y=x+2与抛物线y=x2有两个交点,设这两个交点为A、B:
解得:,.
∴A(2,4)、B(﹣1,1);
(2)解法一:设A(m,m2)、B(a,b),
如图1:过A作x轴垂线,过P、B作y轴垂线,交于点F,
∵PA=AB,
在△ABF和△APE中,
,
∴△ABF≌△APE(AAS)
∴B的横坐标a=2m﹣2,纵坐标b=m2﹣(2﹣m2)=2m2﹣2
∵点B在抛物线上,b=a2,∴2 m2﹣2=(2 m﹣2)2,
解得m=1或m=3,∴得点A(1,1)或A(3,9)
∵P(2,2),
∴设直线m的解析式为:y=kx+b,
,
解得:,
∴直线m的解析式为:y=x,
同理可得出:直线m的解析式为:y=7x﹣12,
综上所述:直线m的解析式为:y=x 或y=7x﹣12;
(解法二:设B(a,a2),∵PA=AB,∴A是线段PB的中点,∴A(,),
∵A在抛物线上,∴()2=,
解得:∴a=0或4,∴B(0,0)、B(4,16),即可求出直线m的解析式);
(3)设直线m:y=kx+b)k≠0)交y轴于D,设A(x1,),B(x2,).
如图2,过A、B分别作AE、BF垂直x轴于E、F,
∵∠AOB=90°,
∴∠BOF+∠AOE=90°,
∵∠FBO+∠BOF=90°,
∴∠FBO=∠AOE,
∵∠BFO=∠AEO,
∴△AEO∽△OFB,
∴=,
∴=,∴x1x2=﹣1,
∵A、B是y=kx+b与y=x2的交点,
∴x1,x2是kx+b=x2的解,
∴x=由x1x2=﹣1,
解得:b=1,∴D(0,1),
∵∠BPC=∠OCP,∴DP=DC=3,
过P作PG垂直y轴于G,则:PG2+GD2=DP2,
∴设P(a,2a﹣2),有a2+(2a﹣2﹣1)2=32,
解得:a=0(舍去)或a=,
∴P(,).
19.
解:(1)设OA=x,则OB=10﹣x,
∴∠ABC=∠ACO,∠AOC=∠COB,
∴△BOC~△C0A,
∴=,
∴OC2=OA×OB,
∴16=x(10﹣x),
∴x=8或x=2,
∴A(2,0),B(﹣8,0),
设抛物线的解析式为y=a(x+8)(x﹣2)
∴4=(0+8)(0﹣2),
∴a=﹣,
∴y=﹣(x+8)(x﹣2)=﹣x2﹣x+4.
(2)
①∵B(﹣8,0),C(0,4),
∴直线BC的解析式为y=x+4,
设E(m,m+4),且B(﹣8,0),D(0,4),
∴BE=,DE=,BD=4,
∵△BDE为等腰三角形,
Ⅰ、当BE=DE时,有=,
∴m=﹣6,
∴m+4=1,
∴E(﹣6,1),
Ⅱ、当BE=BD时,有=4,
∴m=或m=,
∴E(,),E(,﹣),
Ⅲ、当BD=DE时,有=4,
∴m=﹣或m=﹣8(舍)
∴E(﹣,),
∴E(﹣6,1),E(,),E(,﹣),E(﹣,).
②∵C(0,4),D(﹣4,0),
∴直线CD的解析式为y=x+4,
作PF⊥CD,设直线PF的解析式为y=﹣x+b,
∴F(,),
设P(m,﹣m+b),
∴﹣m+b=﹣m2﹣m+4,
∴b=﹣m2﹣m+4,
∵P(﹣m,﹣m+b),F(,),C(0,4),
∴CF==,
PF==,
∵tan∠CBD=,∠CBD=∠PCF,
∴tan∠PCF==,
∴CF=2PF,
∴=2×,
∴m=﹣或m=﹣18,
∴b=﹣m2﹣m+4=﹣或b=﹣m2﹣m+4=﹣68,
∴P(﹣,)或P(﹣18,﹣50).
1.C
解:当y=0时,x=﹣2,即与x轴交点是(﹣2,0),故①正确;
当x=0时,y=6,即与y轴的交点是(0,6),故②正确;
由上表可知当x=0和x=1时,y=6所以对称轴x==,故③正确;
由③可知,+(+2)=3,即抛物线与x轴的另一个交点为(3,0)故④正确;
由上表可看出,y的值在x=0,y=6的左侧是随着x的增大而增大的,故⑤错误.
①②③④正确,故选C.
2. D
3.B
解:由点是该抛物线的顶点,且,所以
为函数的最小值,即得出抛物线的开口向上,因为,所以得出点A、B可能在对称轴的两侧或者是在对称轴的左侧,当在对称轴的左侧时,y随x的增大而减小,因此>3,当在对称轴的两侧时,点B距离对称轴的距离小于点A到对称轴的距离,即得-(-5)>3-,解得,综上所得:,故选B
4. D
解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣=1,
∴b=﹣2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③正确;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=﹣,
∵b=﹣2a,
∴x1+x2=2,所以⑤正确.
5. ②⑤
解:∵函数y=x2+bx+c与x轴无交点,
∴b2﹣4ac<0;
∴b2﹣4c<0
故①不正确;
当x=3时,y=9+3b+c=3,
∴3b+c+6=0
故②正确;
从图象可知当x2+bx+c>1时,x<1或x>2
③不正确;
④过顶点(,)的反比例函数为y=,
由图象可知,当x2+bx+c>时,x>或x<0,
④错误.
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故⑤正确.
故答案为:②⑤
6.解:①把y=8代入y=2x得:
8=2x,
解得x=4,
即在直线y=2x上,当函数值y≤8时,对应的自变量x的取值范围是x≤4;
②把y=8代入y=x2+2=8,
解得:x=±,
∵x≤2,
∴x=舍去,
即根据图象可知,当函数值y≤8时,对应的自变量x的取值范围是x≥﹣;
综合①②得出当函数值y≤8时,对应的自变量x的取值范围是﹣≤x≤4.
故答案为:﹣≤x≤4.
7.解:∵y=kx+3﹣3k=k(x﹣3)+3,
∴当x﹣3=0,即x=3时,不论k为何值,y=3,
故y=kx+3﹣3k必过定点(3,3);
①联立得,
(x﹣1)2﹣1=kx+3﹣3k,
整理得,x2﹣(k+2)x+3(k﹣1)=0,
△=(k+2)2﹣12(k﹣1)=(k﹣4)2≥0,
当k=4时,△=0只有一个根,
当k≠4时,△>0有两个根,
∵x≤3,由图可知,
∴k≥4时,y=kx+3﹣3k与y=(x﹣1)2﹣1只有一个交点;
②联立得,
(x﹣5)2﹣1=kx+3﹣3k,
整理得,x2﹣(k+10)x+3(k+7)=0,
△=(k+10)2﹣12(k+7)=(k+4)2≥0,
当k=﹣4时,△=0只有一个根,
当k≠﹣4时,△>0有两个根,
∵x>3,由图可知,
∴k≤﹣4时,y=kx+3﹣3k与y=(x﹣5)2﹣1没有一个交点;
综上所述,k≥4时,y=kx+3﹣3k与y=(x﹣1)2﹣1有一个交点,与y=(x﹣5)2﹣1有一个交点,
k≤﹣4时,y=kx+3﹣3k与y=(x﹣5)2﹣1没有一个交点,与y=(x﹣1)2﹣1有两个交点,
所以,k≥4或k≤﹣4时,两函数只有两个交点.
故答案为:(3,3);k≥4或k≤﹣4.
8. ﹣1<k<3
解:函数的图象为:
9.
解:(1)根据定义,点M坐标为(﹣1,2).
故答案为(﹣1,2).
(2)当y=﹣16时,x2=32,x=±4,
∵若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16,
∴0≤a≤4.
10.
解:(1)设李明第n天生产的粽子数量为420只,
由题意可知:30n+120=420,
解得n=10.
答:第10天生产的粽子数量为420只.
(2)由图象得,当0≤x≤<时,p=4.1;
当9≤x≤15时,设P=kx+b,
把点(9,4.1),(15,4.7)代入得,,
解得,
∴p=0.1x+3.2,
①0≤x≤5时,w=(6﹣4.1)×54x=102.6x,当x=5时,w最大=513(元);
②5<x≤9时,w=(6﹣4.1)×(30x+120)=57x+228,
∵x是整数,
∴当x=9时,w最大=741(元);
③9<x≤15时,w=(6﹣0.1x﹣3.2)×(30x+120)=﹣3x2+72x+336,
∵a=﹣3<0,
∴当x=﹣=12时,w最大=768(元);
综上,当x=12时,w有最大值,最大值为768.
(3)由(2)可知m=12,m+1=13,
设第13天提价a元,由题意得,w13=(6+a﹣p)(30x+120)=510(a+1.5),
∴510(a+1.5)﹣768≥48,解得a=0.1.
答:第13天每只粽子至少应提价0.1元.
11.
(1)解:∵a1=﹣1,b1=3,c1=﹣2,
∴﹣1+a2=0,b2=3,﹣2+c2=0,
∴a2=1,b2=3,c2=2,
∴函数y=﹣x2+3x﹣2的“旋转函数”为y=x2+3x+2;
(2)解:根据题意得m=﹣2n,﹣2+n=0,解得m=﹣3,n=2,
∴(m+n)2015=(﹣3+2)2015=﹣1;
(3)证明:当x=0时,y=﹣(x+1)(x﹣4)=2,则C(0,2),
当y=0时,﹣(x+1)(x﹣4)=0,解得x1=﹣1,x2=4,则A(﹣1,0),B(4,0),
∵点A、B、C关于原点的对称点分别是A1,B1,C1,
∴A1(1,0),B1(﹣4,0),C1(0,﹣2),
设经过点A1,B1,C1的二次函数解析式为y=a2(x﹣1)(x+4),把C1(0,﹣2)代入得a2•(﹣1)•4=﹣2,解得a2=,
∴经过点A1,B1,C1的二次函数解析式为y=(x﹣1)(x+4)=x2+x﹣2,
而y=﹣(x+1)(x﹣4)=﹣x2+x+2,
∴a1+a2=﹣+=0,b1=b2=,c1+c2=2﹣2=0,
∴经过点A1,B1,C1的二次函数与函数y=﹣(x+1)(x﹣4)互为“旋转函数.
12.
解:(1)设函数解析式为:y=ax2+bx+c,
由函数经过点A(﹣4,0)、B(1,0)、C(﹣2,6),
可得,
解得:,
故经过A、B、C三点的抛物线解析式为:y=﹣x2﹣3x+4;
(2)设直线BC的函数解析式为y=kx+b,
由题意得:,
解得:,
即直线BC的解析式为y=﹣2x+2.
故可得点E的坐标为(0,2),
从而可得:AE==2,CE==2,
故可得出AE=CE;
(3)相似.理由如下:
设直线AD的解析式为y=kx+b,
则,
解得:,
即直线AD的解析式为y=x+4.
联立直线AD与直线BC的函数解析式可得:,
解得:,
即点F的坐标为(﹣,),
则BF==,AF==,
又∵AB=5,BC==3,
∴=,=,
∴=,
又∵∠ABF=∠CBA,
∴△ABF∽△CBA.
故以A、B、F为顶点的三角形与△ABC相似.
13.
解:(1)证明:∵若m=1时,函数为一次函数,与x轴有交点
若时,函数为二次函数,=0
△ =
∴不论m为何值,该函数的图像与x轴总有交点
(2)∵(0,0) 代入得
m=2
∴y=
∴交点M(-1,0)
(3)顶点为
向上平移个单位
围成部分面积利用平移转化成
∴面积为
14.
解:当k分别取0,1,2时,所对应的函数为,,.
①令=,求出=的解,得到两函数图象的交点(1,0),(-1,2) ,
y1>y 2时观察图象可得结论正确.
②当k=1时,得直线,函数图象一定是y随x的增大而减小;
当k>1时,求出函数的对称轴得直线,且二次函数图象开口向上,在对称轴的左侧,函数图象y随x的增大而减小.所以当k≥1时,结论正确.
③的顶点坐标是(,),的顶点坐标是(,),可得两顶点的中点坐标是P(0, 1),且与图象的形状相同,方向相反,关于顶点中心对称成立则整个图象亦成立,所以结论正确.
④当=时,得交点坐标A(1,0),B(-1,2),AB中点为P(0, 1). 当k=1时,得直线,得与y轴的交点C(0,1),点A,B,C在同一直线,不存在;
当k>1时,抛物线图象开口向上,与y轴交点为(0,2-k).若点C为直角顶点,由PC=PA得,显然k无整数解;同理,当k<1时,由中心对称可知,k无整数解.综上所述,整数k不存在,结论错误.
15.
方法一:
解:(1)∵抛物线y=ax2+bx+c(a≠0)过点C(0,4),
∴c=4 ①.
∵对称轴x=﹣=1,
∴b=﹣2a ②.
∵抛物线过点A(﹣2,0),
∴0=4a﹣2b+c ③,
由①②③解得,a=﹣,b=1,c=4,
∴抛物线的解析式为y=﹣x2+x+4;
(2)假设存在满足条件的点F,如图所示,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.
设点F的坐标为(t,﹣t2+t+4),其中0<t<4,
则FH=﹣t2+t+4,FG=t,
∴S△OBF=OB•FH=×4×(﹣t2+t+4)=﹣t2+2t+8,
S△OFC=OC•FG=×4×t=2t,
∴S四边形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12.
令﹣t2+4t+12=17,
即t2﹣4t+5=0,
则△=(﹣4)2﹣4×5=﹣4<0,
∴方程t2﹣4t+5=0无解,
故不存在满足条件的点F;
(3)设直线BC的解析式为y=kx+n(k≠0),
∵B(4,0),C(0,4),
∴,
解得,
∴直线BC的解析式为y=﹣x+4.
由y=﹣x2+x+4=﹣(x﹣1)2+,
∴顶点D(1,),
又点E在直线BC上,则点E(1,3),
于是DE=﹣3=.
若以D、E、P、Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,
设点P的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣m2+m+4).
①当0<m<4时,PQ=(﹣m2+m+4)﹣(﹣m+4)=﹣m2+2m,
由﹣m2+2m=,
解得:m=1或3.
当m=1时,线段PQ与DE重合,m=1舍去,
∴m=3,P1(3,1).
②当m<0或m>4时,PQ=(﹣m+4)﹣(﹣m2+m+4)=m2﹣2m,
由m2﹣2m=,
解得m=2±,经检验适合题意,
此时P2(2+,2﹣),P3(2﹣,2+).
综上所述,满足题意的点P有三个,分别是P1(3,1),P2(2+,2﹣),P3(2﹣,2+).
方法二:
(1)略.
(2)∵B(4,0),C(0,4),
∴lBC:y=﹣x+4,
过F点作x轴垂线,交BC于H,设F(t,﹣t2+t+4),
∴H(t,﹣t+4),
∵S四边形ABFC=S△ABC+S△BCF=17,
∴(4+2)×4+(﹣t2+t+4+t﹣4)×4=17,
∴t2﹣4t+5=0,
∴△=(﹣4)2﹣4×5<0,
∴方程t2﹣4t+5=0无解,故不存在满足条件的点F.
(3)∵DE∥PQ,
∴当DE=PQ时,以D、E、P、Q为顶点的四边形是平行四边形,
∵y=﹣x2+x+4,
∴D(1,),
∵lBC:y=﹣x+4,
∴E(1,3),
∴DE=﹣3=,
设点F的坐标是(m,﹣m+4),则点Q的坐标是(m,﹣m2+m+4),
∴|﹣m+4+m2﹣m﹣4|=,
∴m2﹣2m=或m2﹣2m=﹣,
∴m=1,m=3,m=2+,m=2﹣,
经检验,当m=1时,线段PQ与DE重合,故舍去.
∴P1(3,1),P2(2+,2﹣),P3(2﹣,2+).
16.
解:(1)∵抛物线y=ax2+bx+c过点A(﹣2,0),B(8,0),C(0,﹣4),
∴,解得,
∴抛物线的解析式为:y=x2﹣x﹣4;
∵OA=2,OB=8,OC=4,∴AB=10.
如答图1,连接AC、BC.
由勾股定理得:AC=,BC=.
∵AC2+BC2=AB2=100,
∴∠ACB=90°,
∴AB为圆的直径.
由垂径定理可知,点C、D关于直径AB对称,
∴D(0,4).
(2)解法一:
设直线BD的解析式为y=kx+b,∵B(8,0),D(0,4),
∴,解得,
∴直线BD解析式为:y=﹣x+4.
设M(x,x2﹣x﹣4),
如答图2﹣1,过点M作ME∥y轴,交BD于点E,则E(x,﹣x+4).
∴ME=(﹣x+4)﹣(x2﹣x﹣4)=﹣x2+x+8.
∴S△BDM=S△MED+S△MEB=ME(xE﹣xD)+ME(xB﹣xE)=ME(xB﹣xD)=4ME,
∴S△BDM=4(﹣x2+x+8)=﹣x2+4x+32=﹣(x﹣2)2+36.
∴当x=2时,△BDM的面积有最大值为36;
解法二:
如答图2﹣2,过M作MN⊥y轴于点N.
设M(m,m2﹣m﹣4),
∵S△OBD=OB•OD==16,
S梯形OBMN=(MN+OB)•ON
=(m+8)[﹣(m2﹣m﹣4)]
=﹣m(m2﹣m﹣4)﹣4(m2﹣m﹣4),
S△MND=MN•DN
=m[4﹣(m2﹣m﹣4)]
=2m﹣m(m2﹣m﹣4),
∴S△BDM=S△OBD+S梯形OBMN﹣S△MND
=16﹣m(m2﹣m﹣4)﹣4(m2﹣m﹣4)﹣2m+m(m2﹣m﹣4)
=16﹣4(m2﹣m﹣4)﹣2m
=﹣m2+4m+32
=﹣(m﹣2)2+36;
∴当m=2时,△BDM的面积有最大值为36.
(3)如答图3,连接AD、BC.
由圆周角定理得:∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOD∽△COB,
∴=,
设A(x1,0),B(x2,0),
∵已知抛物线y=x2+bx+c(c<0),
∵OC=﹣c,x1x2=c,
∴=,
∴OD==1,
∴无论b,c取何值,点D均为定点,该定点坐标D(0,1).