中考数学探究题专题训练中考总复习

中考数学探究题专题训练中考总复习

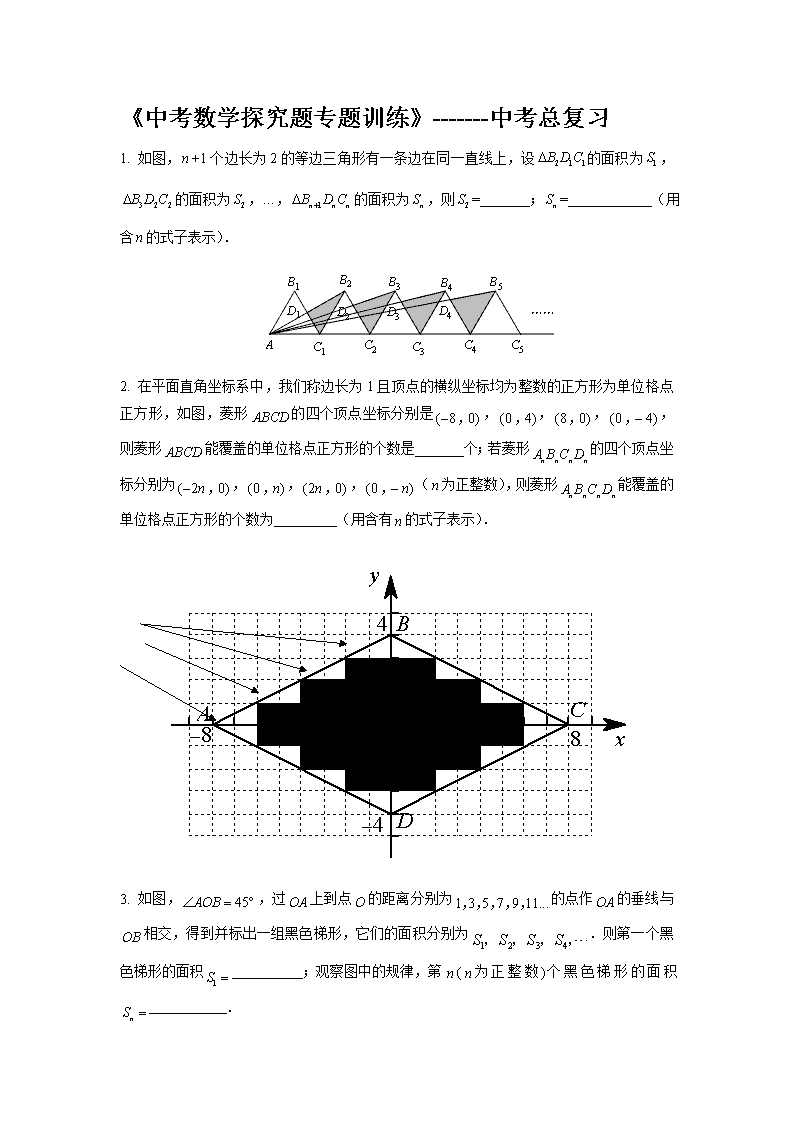
‎《中考数学探究题专题训练》-------中考总复习 ‎1. 如图，+1个边长为2的等边三角形有一条边在同一直线上，设的面积为，的面积为，…，的面积为，则= ；=____ （用含的式子表示）．‎ ‎2. 在平面直角坐标系中，我们称边长为1且顶点的横纵坐标均为整数的正方形为单位格点 正方形，如图，菱形的四个顶点坐标分别是，，，，则菱形能覆盖的单位格点正方形的个数是_______个；若菱形的四个顶点坐标分别为，，，（为正整数），则菱形能覆盖的单位格点正方形的个数为_________（用含有的式子表示）．‎ ‎3. 如图，，过上到点的距离分别为的点作的垂线与相交，得到并标出一组黑色梯形，它们的面积分别为．则第一个黑色梯形的面积 ；观察图中的规律，第(为正整数)个黑色梯形的面积 ．‎ ‎4. 在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点．请你观察图中正方形A1B‎1C1D1，A2B‎2C2D2，A3B‎3C3D3……每个正方形四条边上的整点的个数．按此规律推算出正方形A10B‎10C10D10四条边上的整点共有　　　个．‎ ‎5. 如图，△ABC中，∠ACB=90°，AC=BC=1，取斜边的中点，向斜边做垂线，画出一个新的等腰直角三角形，如此继续下去，直到所画直角三角形的斜边与△ABC的BC边重叠为止，此时这个三角形的斜边长为_____．‎ ‎6.如图，以等腰三角形的斜边为直角边向外作第个等腰直角三角形，再以等腰直角三角形的斜边为直角边向外作第个等腰直角三角形，……，如此作下去，若，则第个等腰直角三角形的面积 ________（n为正整数）.‎ ‎7. 如图，在平面直角坐标系xOy中，，，，‎ ‎，…，以为对角线作第一个正方形，以 为对角线作第二个正方形，以为对角线作第 三个正方形，…，如果所作正方形的对角线都在 y轴上，且的长度依次增加1个单位，顶点都在第一象 限内（n≥1，且n为整数）．那么的纵坐标为 ；用n 的代数式表示的纵坐标： ．‎ ‎8. 如图，在平面直角坐标系中，一颗棋子从点处开始跳动，第一 次跳到点关于x轴的对称点处，接着跳到点关于y轴 的对称点 处，第三次再跳到点关于原点的对称点处，…，‎ 如此循环下去．当跳动第2009次时，棋子落点处的坐标是 ‎ ． ‎ ‎1‎ ‎3‎ ‎1‎ ‎3‎ ‎5‎ ‎9.对于大于或等于2的自然数n的平方进行如下“分裂”，分裂成n个连续奇数的和，则自然数72的分裂数中最大的数是 ，自然数n的分裂数中最大的数是 .‎ ‎ ‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ x y ‎1‎ ‎2‎ ‎3‎ ‎…‎ ‎10.一个质点在第一象限及轴、轴上运动，在第一秒钟，它从原点运动到，然后接着按图中箭头所示方向运动,即，且每秒移动一个单位，那么第35秒时质点所在位置的坐标是_______‎ ‎11.如图，将边长为的正方形纸片从左到右顺次摆放，其对应的正方形的中心依次为A1, A2, A3, ….①若摆放前6‎ 个正方形纸片，则图中被遮盖的线段（虚线部分）‎ 之和为 ；②若摆放前n（n为大于1的正 整数）个正方形纸片，则图中被遮盖的线段（虚线部分）之和为 .‎ ‎12、如图，每一幅图中有若干个大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第n幅图中共有 个。‎ ‎…‎ ‎…‎ 第1幅 第2幅 第3幅 第n幅 ‎13、用正三角形、正四边形和正六四边形按如图所示的规律拼图案，即从第二个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个．则第n个图案中正三角形的个数为 。 ‎ ‎…‎ 第一个图案 第二个图案 第三个图案 条射线，可14. 如图 在锐角内部，画1得3个锐角；画2条不同射线，可得6个锐角；画3条不同射线，可得10个锐角；……照此规律，画n条不同射线，可得锐角 ‎ ‎ ______个．‎ ‎…‎ ‎15、在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，在图（2）中，A2、B2、C2分别是△A1B‎1C1的边B‎1C1、C‎1 A1、 A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有 个。‎ ‎16、、如图，△ABC的面积为1，分别取AC、BC两边的中点A1、B1，则四边形A1ABB1的面积为，再分别取A‎1C、B‎1C的中点A2、B2，A‎2C、B‎2C的中点A3、B3，依次取下去…．利用这一图形，能直观地计算出＋＋＋…＋＝________‎ AD BAD CFEBAD A1‎ A2‎ A3‎ B1‎ B2‎ B3‎ A B C D B E D A C ‎（第19题图）‎ 附：参考答案 ‎1.‎ ‎2. 48 ‎ ‎3. =8n-4. ‎ ‎4. 80‎ ‎5. ‎ ‎6. ‎ ‎7. 2；‎ ‎8. （3，－2）‎ ‎9. 13；2n-1‎ ‎10. （5，0） ‎ ‎11. 10，‎ ‎12. 2n-1‎ ‎13. 4n+2‎ ‎14. ‎ ‎15. 4n+1‎ ‎16 ‎ 全 品 中 考 考 网 全 品 中 考 网