- 2021-05-10 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考总复习三角形全等与相似
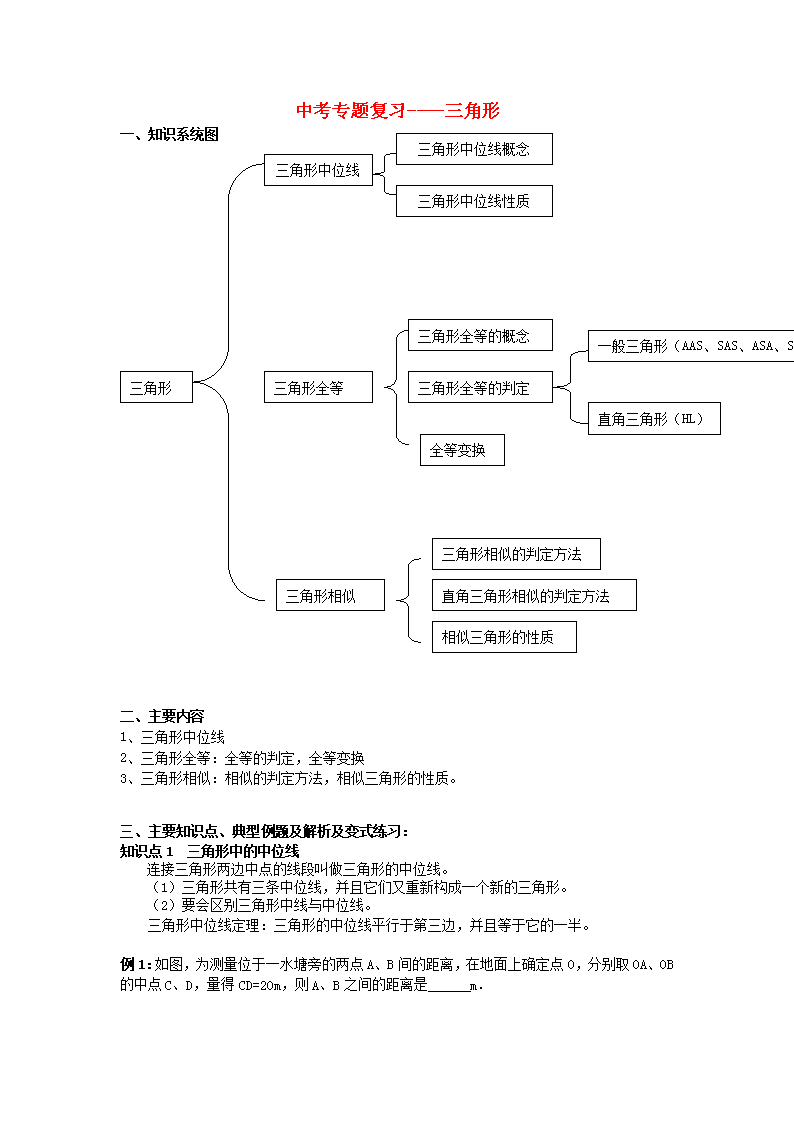
中考专题复习----三角形 三角形中位线概念 一、知识系统图 三角形中位线 三角形中位线性质 一般三角形(AAS、SAS、ASA、SSS) ) 三角形全等的概念 三角形全等 三角形全等的判定 三角形 直角三角形(HL) 全等变换 三角形相似的判定方法 直角三角形相似的判定方法 三角形相似 相似三角形的性质 二、主要内容 1、三角形中位线 2、三角形全等:全等的判定,全等变换 3、三角形相似:相似的判定方法,相似三角形的性质。 三、主要知识点、典型例题及解析及变式练习: 知识点1 三角形中的中位线 连接三角形两边中点的线段叫做三角形的中位线。 (1)三角形共有三条中位线,并且它们又重新构成一个新的三角形。 (2)要会区别三角形中线与中位线。 三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。 例1:如图,为测量位于一水塘旁的两点A、B间的距离,在地面上确定点O,分别取OA、OB的中点C、D,量得CD=20m,则A、B之间的距离是 m. 考点:三角形中位线定理。 常作辅助线:各边中点的连线。 分析:根据三角形的中位线平行于第三边并且等于第三边的一半解答即可。 变式练习: 如图,在△ABC中,点D、E分别是AB、AC的中点.若DE=3,则BC= . 知识点2 三角形全等的判定 全等用符号“≌”表示,读作“全等于”。如△ABC≌△DEF,读作“三角形ABC全等于三角形DEF”。 注:记两个全等三角形时,通常把表示对应顶点的字母写在对应的位置上。 (1)边角边定理:有两边和它们的夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”) (2)角边角定理:有两角和它们的夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”) (3)边边边定理:有三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。 推论:角角边定理:两角和一角的领边对应相等的两个三角形全等(可简写成“角角边”或“AAS”) HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”) 例2:如图,在平行四边形ABCD中,过AC中点0作直线,分别交AD、BC于点E、F. 求证:△AOE≌△COF. 考点:平行四边形的性质;全等三角形的判定. 分析:据平行四边形的性质可知:OA=OC,∠AEO=∠OFC,∠EAO=∠OCF,所以△AOE≌△COF. 变式练习: 如图,C是AB的中点,AD=BE,CD=CE. 求证:∠A=∠B. 例3:如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F. (1)求证:DE=BF; (2)连接EF,写出图中所有的全等三角形.(不要求证明) 考点:平行四边形的性质;全等三角形的判定与性质 分析:(1)由平行四边形的性质和已知条件证明四边形DEBF是平行四边形,根据平行四边形的性质可得到DE=BF; (2)连接EF,则图中所有的全等三角形有:△ADE≌△CBF,△DFE≌△BEF 变式练习: 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( ) A. 50° B. 60° C. 70° D. 80° 知识点3 全等变换包括一下三种: (1)平移变换:把图形沿某条直线平行移动的变换叫做平移变换。 (2)对称变换:将图形沿某直线翻折180°,这种变换叫做对称变换。 (3)旋转变换:将图形绕某点旋转一定的角度到另一个位置,这种变换叫做旋转变换。 例4:如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE. (1)求证:AB⊥AE; (2)若BC2=AD•AB,求证:四边形ADCE为正方形. 考点:旋转的性质;全等三角形的判定与性质;等腰直角三角形;正方形的判定;相似三角形的判定与性质 分析:(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论 变式练习:已知:如图,△ABC中,AB=AC,AD⊥BC垂足为D。将△ADC绕点D逆时针旋转90°后,点A落在BD上点A1处,点C落在DA延长线上点C1处,A1 C1与AB交于点E。 求证:△A1BE≌△AC1E 知识点4 三角形相似的判定 (1)三角形相似的判定方法 ①定义法:对应角相等,对应边成比例的两个三角形相似 ②平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似 ③判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似,可简述为两角对应相等,两三角形相似。 ④判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应相等,并且夹角相等,那么这两个三角形相似,可简述为两边对应成比例且夹角相等,两三角形相似。 ⑤判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似,可简述为三边对应成比例,两三角形相似。 (2)直角三角形相似的判定方法 ①以上各种判定方法均适用 ②定理:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似 ③垂直法:直角三角形被斜边上的高分成的两个直角三角形与原三角形相似。 例5:如图,在▱ABCD中,AB=6cm,AD=9cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4cm,则EF+CF的长为 cm. 考点:相似三角形的判定与性质;等腰三角形的判定与性质;勾股定理;平行四边形的性质 分析:首先,由于AE平分∠BAD,那么∠BAE=∠DAE,由AD∥BC,可得内错角∠DAE=∠BEA,等量代换后可证得AB=BE,即△ABE是等腰三角形,根据等腰三角形“三线合一”的性质得出AE=2AG,而在Rt△ABG中,由勾股定理可求得AG的值,即可求得AE的长;然后,利用平行线分线段成比例的性质分别得出EF,FC的长,即可得出答案; 变式练习:如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x,y轴的正半轴上.点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P.则点P的坐标为 . 知识点5 相似三角形的性质 ①相似三角形的对应角相等,对应边成比例 ②相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比 ③相似三角形周长的比等于相似比 ④相似三角形面积的比等于相似比的平方 例6:宽与长之比为的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论. 考点:相似三角形的判定与性质;黄金分割 分析:要由黄金分割的定义推广到黄金矩形 变式练习:将三角形高分为四等分,过每个分点作底边的平行线,将三角形分四个部分,则四个部分面积之比是( ) A.1∶3∶5∶7 B.1∶2∶3∶4 C.1∶2∶4∶5 D.1∶2∶3∶5 四、难点突破方法总结 在求解三角形全等与相似试题中,要突出转化的数学思想,通过转化寻找量和量之间的关系,归纳下来,有这样几个方面值得考生们注意: 1.掌握解题的关键点.(1)有两角,找任意一边;(2)有两边,找夹角;(3)有相似,常需利用相似比求值线段的长度. 2.重视基本定理与基本图形相结合,计算与推理相结合,灵活运用各种方法. 3.重视数学思想方法的应用.运用分析法、演绎法、截补法,结合方程思想、分类讨论思想、数形结合思想解有关圆的应用题,探索开放性题和方案设计. 五、拓展演练 一、选择题: 1.尺规作图作的平分线方法如下:以为圆心,任意长为半径画弧交、于、,再分别以点、为圆心,以大于长为半径画弧,两弧交于点,作射线由作法得的根据是( ) A.SAS B.ASA C.AAS D.SSS 2.如图,将Rt△ABC(其中∠B=34,∠C=90)绕A点按顺时针方向旋转到△AB1 C1的位置,使得点C、A、B1 在同一条直线上,那么旋转角最小等于( ) A.56 B.68 C.124 D.180 3. 如图所示,∠E=∠F=90°, ∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△CAN≌△ABM.其中正确的有( ) A. 1个 B. 2个 C.3个 D.4个 4.如图,在等腰梯形ABCD中,AB=DC,AC、BD交于点O,则图中全等三角形共有( ) A.2对 B.3对 C.4对 D.5对 34 B1 C B A C1 (第5题图) (第4题图) (第3题图) (第2题图) 5.如图,已知等边三角形ABC的边长为2,DE是它的中位线,则下面四个结论:(1)DE=1,(2)△CDE∽△CAB,(3)△CDE的面积与△CAB的面积之比为1:4.其中正确的有 ( ) A.0个 B.1个 C.2个 D.3个 (第6题图) (第5题图) 6.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于( ) A. B. C. D. 7.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值 ( ) A.只有1个 B.可以有2个 C.有2个以上但有限 D.有无数个 二、填空题: 8.如图,中,点的坐标为(0,1),点的坐标为(4,3),如果要使与 全等,那么点的坐标是 . 9.如图,已知,,要使 ≌,可补充的条件是 (写出一个即可). 10.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:① AD=BE ② PQ∥AE ③ AP=BQ ④ DE=DP ⑤∠AOB=60°.恒成立的结论有____ __________(把你认为正确的序号都填上). (第12题图) A B C E D O P Q A C E B D (第10题图) (第9题图) 11.已知△ABC与△DEF相似且对应中线的比为2:3,则△ABC与△DEF的周长比为_____________. 12.如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=6m,点P到CD的距离是2.7m,则AB与CD间的距离是__________. 三、解答题: 13.两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,在同一条直线上,连结. (1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); 图1 图2 (2)证明:. 14.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。 15.如图,在ABC中,已知DE∥BC,AD=4,DB=8,DE=3, (1)求的值,(2)求BC的长 16.如图,在方格纸中 (1)请在方格纸上建立平面直角坐标系,使,并求出点坐标; A B C (2)以原点为位似中心,相似比为2,在第一象限内将放大,画出放大后的图形; (3)计算的面积. 17.正方形边长为4,、分别是、上的两个动点,当 点在上运动时,保持和垂直, (1)证明:; (2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积; (3)当点运动到什么位置时,求的值.查看更多