中考数学综合提升训练圆中有关的辅助线

中考数学综合提升训练圆中有关的辅助线

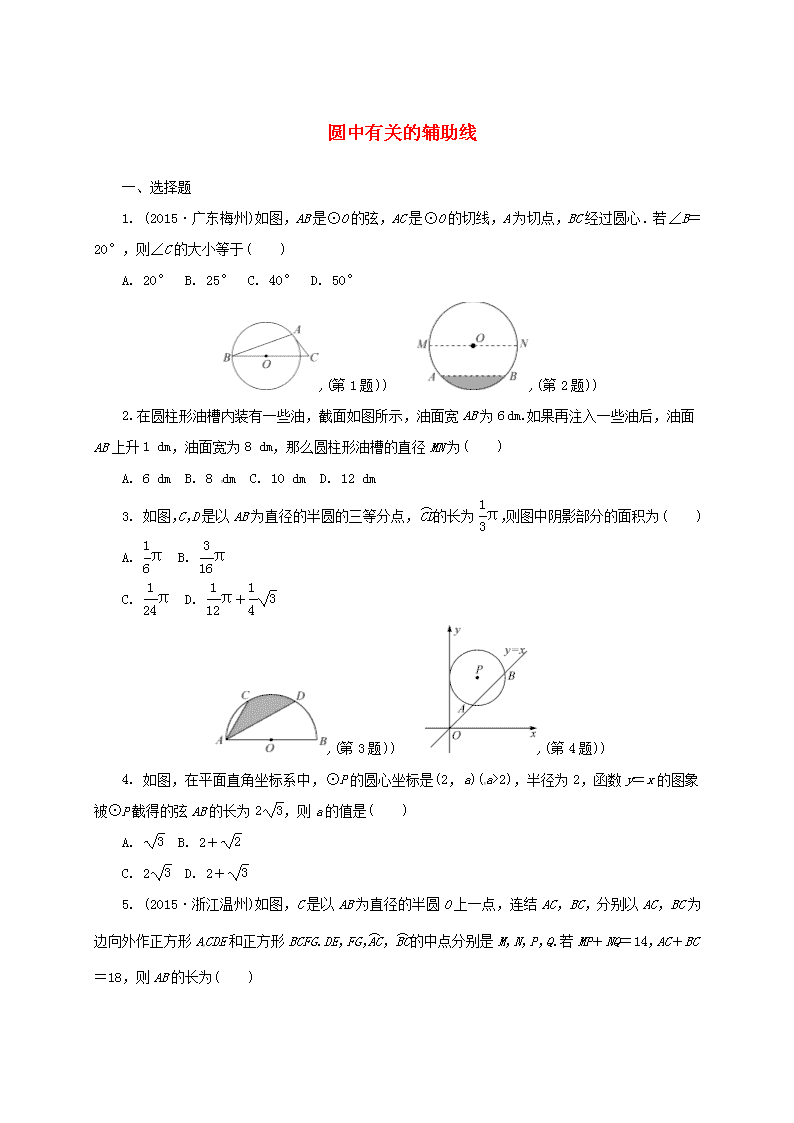
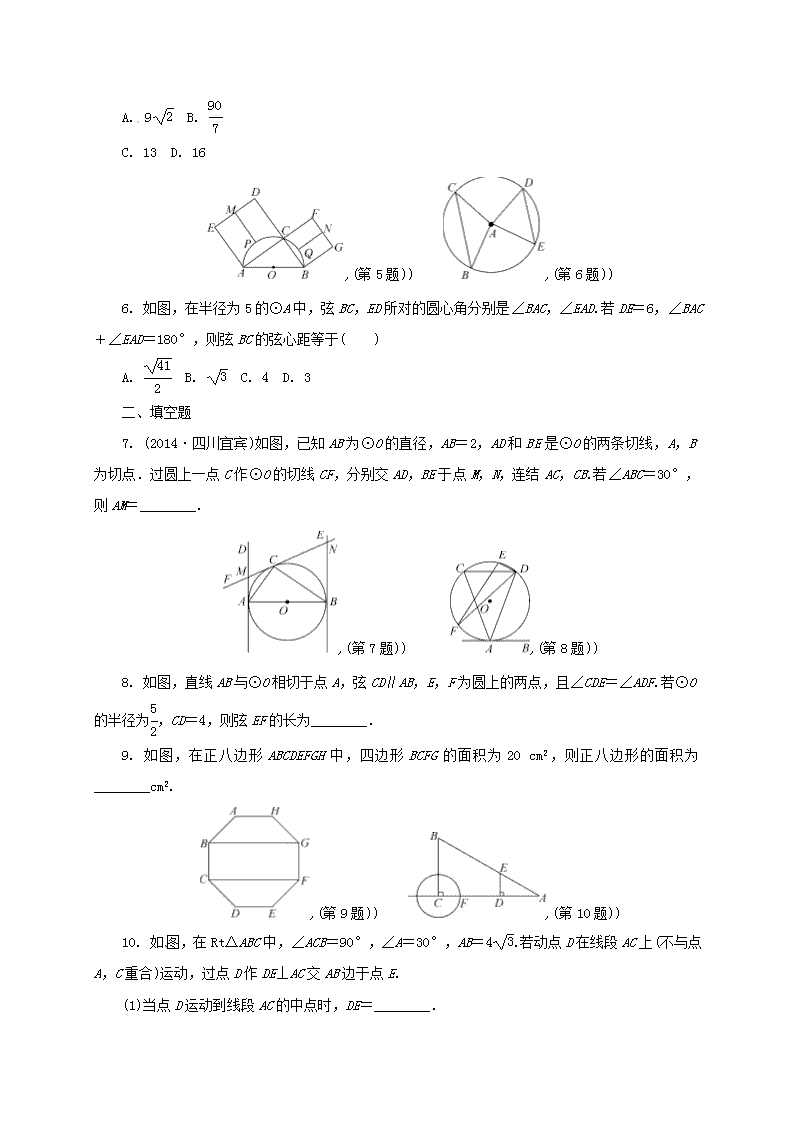
圆中有关的辅助线 一、选择题 ‎1. (2015·广东梅州)如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B＝20°，则∠C的大小等于(　　)‎ A. 20° B. 25° C. 40° D. 50°‎ ‎,(第1题))　　,(第2题))‎ ‎2. 在圆柱形油槽内装有一些油，截面如图所示，油面宽AB为6 dm.如果再注入一些油后，油面AB上升1 dm，油面宽为8 dm，那么圆柱形油槽的直径MN为(　　)‎ A. 6 dm B. 8 dm C. 10 dm D. 12 dm ‎3. 如图，C，D是以AB为直径的半圆的三等分点，的长为π，则图中阴影部分的面积为(　　)‎ A. π B. π C. π D. π＋ ‎,(第3题))　　,(第4题))‎ ‎4. 如图，在平面直角坐标系中，⊙P的圆心坐标是(2，a)(a>2)，半径为2，函数y＝x的图象被⊙P截得的弦AB的长为2，则a的值是(　　)‎ A. B. 2＋ C. 2 D. 2＋ ‎5. (2015·浙江温州)如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC，BC为边向外作正方形ACDE和正方形BCFG.DE，FG，，的中点分别是M，N，P，Q.若MP＋NQ＝14，AC＋BC＝18，则AB的长为(　　)‎ A. 9 B. C. 13 D. 16‎ ‎,(第5题))　　,(第6题))‎ ‎6. 如图，在半径为5的⊙A中，弦BC，ED所对的圆心角分别是∠BAC，∠EAD.若DE＝6，∠BAC＋∠EAD＝180°，则弦BC的弦心距等于(　　)‎ A. B. C. 4 D. 3‎ 二、填空题 ‎7. (2014·四川宜宾)如图，已知AB为⊙O的直径，AB＝2，AD和BE是⊙O的两条切线，A，B为切点．过圆上一点C作⊙O的切线CF，分别交AD，BE于点M，N，连结AC，CB.若∠ABC＝30°，则AM＝________．‎ ‎,(第7题))　　　,(第8题))‎ ‎8. 如图，直线AB与⊙O相切于点A，弦CD∥AB，E，F为圆上的两点，且∠CDE＝∠ADF.若⊙O的半径为，CD＝4，则弦EF的长为________．‎ ‎9. 如图，在正八边形ABCDEFGH中，四边形BCFG的面积为‎20 cm2，则正八边形的面积为________cm2.‎ ‎,(第9题))　　,(第10题))‎ ‎10. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4.若动点D在线段AC上(不与点A，C重合)运动，过点D作DE⊥AC交AB边于点E.‎ ‎(1)当点D运动到线段AC的中点时，DE＝________．‎ ‎(2)若点A关于点D的对称点为F，以FC为半径作⊙C，当DE＝________时，⊙C与直线AB相切．‎ 三、解答题 ‎11. 如图，AC，BD为⊙O的两条弦，且AC⊥BD，⊙O的半径为，求AB2＋CD2的值．‎ ‎(第11题)‎ ‎12. (2015·浙江丽水)如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E.过点D作⊙O的切线DF，交AC于点F.‎ ‎(第12题)‎ ‎(1)求证：DF⊥AC.‎ ‎(2)若⊙O的半径为4，∠CDF＝22.5°，求阴影部分的面积．‎ ‎13. 如图，⊙O是△ABC的内切圆，⊙O与AB，BC，CA分别相切于点D，E，F，∠DEF＝45°.连结BO并延长，交AC于点G，AB＝4，AG＝2.求：‎ ‎(1)∠A的度数．‎ ‎(2)⊙O的半径．‎ ‎(第13题)‎ ‎14. 如图，已知⊙O的半径为2，弦AB的长为2，C与D分别是劣弧与优弧上的任意一点(点C，D均不与点A，B重合)．‎ ‎(1)求∠ACB的度数．‎ ‎(2)求△ABD的最大面积．‎ ‎(第14题)‎ ‎15. (2014·江苏苏州)如图，已知⊙O上依次有A，B，C，D四点，＝，连结AB，AD，BD，弦AB不经过圆心O，延长AB到点E，使BE＝AB，连结EC，F是EC的中点，连结BF.‎ ‎(1)若⊙O的半径为3，∠DAB＝120°，求的长．‎ ‎(2)求证：BF＝BD.‎ ‎(3)设G是BD的中点，探索：在⊙O上是否存在一点P(不同于点B)，使得PG＝PF？并说明PB与AE的位置关系．‎ ‎(第15题)‎ ‎ ‎1．D 2．C[设AB上升1 dm后的油面为PQ，如解图，过点O作OC⊥AB于点C，交PQ于点D，连结OP，OA．可得AC＝3，PD＝4，CD＝1．设OM＝R．∵OC＝OD＋CD，∴＝＋1，解得R＝5(负值舍去)．∴MN＝10 dm．]‎ ‎(第2题解)‎ ‎3．A[∵点C，D三等分半圆，∴的度数为60°，∴＝π，∴R＝1．连结OC，OD，CD，则△OCD为正三角形，且CD∥AB，∴S△ACD＝S△OCD．∴S阴影＝S扇形OCD＝πR2＝π．]　4．B[易知点P到AB的距离为d＝＝1．过点P作PQ⊥x轴于点Q，交直线y＝x于点C．则CQ＝OQ＝2，PC＝d＝，∴a＝PQ＝＋2．]　5．C[连结OP，OQ，分别交AC，BC于点K，J．∵P是的中点，∴OP⊥AC，∴OP∥BC，K是AC的中点，∴MK∥BC，∴M，P，K，O四点共线．同理可得N，Q，J，O四点共线，J是BC的中点．∴OK＝BC，OJ＝AC，∴OK＋OJ＝(BC＋AC)＝9，PK＋QJ＝(MK＋NJ)－(MP＋NQ)＝18－14＝4，∴AB＝OP＋OQ＝OK＋PK＋OJ＋QJ＝9＋4＝13．]　6．D[过点A作AH⊥BC于点H，作直径CF，连结BF．∵∠BAC＋∠EAD＝180°，∠BAC＋∠BAF＝180°，∴∠DAE＝∠BAF．又∵AD＝AB，AE＝AF，∴△ADE≌△ABF(SAS)，∴BF＝DE＝6．∵AH⊥BC，∴CH＝BH．又∵CA＝AF，∴AH为△CBF的中位线，∴AH＝BF＝3．]　7．[连结OM，OC．∵OB＝OC，∠ABC＝30°，∴∠BCO＝∠ABC＝30°．∵∠AOC为△BOC的外角，∴∠AOC＝2∠ABC＝60°．∵MA，MC分别为⊙O的切线，∴MA＝MC，∠MAO＝∠MCO＝90°．在Rt△AOM和Rt△COM中，∵ ∴Rt△AOM≌Rt△COM(HL)，∴∠AOM＝∠COM＝∠AOC＝30°．在Rt△AOM中，∵OA＝AB＝1，∠AOM＝30°，∴AM＝OA·tan 30°＝．]　8．2[连结AO并延长交CD于点H，连结OC．∵直线AB与⊙O相切于点A，∴OA⊥AB．∵弦CD∥AB，∴AH⊥CD，∴CH＝CD＝×4＝2．∵OA＝OC＝，∴OH＝＝＝，∴AH＝OA＋OH＝＋＝4，∴AC＝＝＝2．∵∠CDE＝∠ADF，∴＝，∴＋＝＋，即＝‎ ，∴EF＝AC＝2．]　9．40[连结HE，AD，设HE与BG相交于点M，AD与BG相交于点N．在正八边形ABCDEFGH中，易得HE⊥BG，AD⊥BG．∵正八边形的每个内角为＝135°，∴∠HGM＝45°，∴MH＝MG．设MH＝MG＝x，则HG＝AH＝AB＝GF＝x，∴BG·GF＝(2x＋x)x＝2(＋1)x2＝20，∴四边形ABGH的面积＝(AH＋BG)·HM＝(＋1)x2＝10，∴正八边形的面积为10×2＋20＝40(cm2)．]　10．(1)[∵∠ACB＝90°，∠A＝30°，AB＝4，∴BC＝AB＝2，AC＝6．∵∠ACB＝90°，DE⊥AC，∴DE∥BC．∵D为AC的中点，∴E为AB的中点，∴DE＝BC＝．]　(2)或[过点C作CH⊥AB于点H．又∵∠A＝30°，AC＝6，∴CH＝3．分为两种情况：①如解图①．∵CF＝CH＝3，∴AF＝6－3＝3．∵点A和点F关于点D对称，∴AD＝DF＝AF＝．∵DE⊥AC，∠A＝30°，∴DE＝AD·tan 30°＝．‎ ‎,(第10题解①))　　,(第10题解②))‎ ‎②如解图②．同理于①，可得DE＝．]　11．1．　12．(1)提示：连结OD，证OD∥AC．　(2)4π－8．　13．(1) 90°．(2)．　14．(1)连结OA，OB，过点O作OE⊥AB于点E．∵OA＝OB，∴AE＝BE．在Rt△AOE中，∵OA＝2，AE＝AB＝，∴OE＝＝1，∴∠OAE＝30°，∴∠AOE＝60°，∴∠AOB＝2∠AOE＝120°．∵∠ADB＝∠AOB，∴∠ADB＝60°．∵四边形ACBD为圆内接四边形，∴∠ACB＋∠ADB＝180°，∴∠ACB＝180°－∠ADB＝120°．　(2)过点D作DF⊥AB，垂足为F，则S△ABD＝×2DF．显然，当DF经过圆心O时，DF取得最大值，从而S△ABD取得最大值，此时DF＝DO＋OF＝2＋1＝3，S△ABD＝×2×3＝3，∴△ABD的最大面积是3．　15．(1)连结OB，OD．∵∠DAB＝120°，∴∠BOD＝2×(180°－120°)＝120°．∵⊙O的半径为3，∴的长为＝2π．　(2)连结AC．∵AB＝BE，∴B为AE的中点．又∵F是EC的中点，∴BF为△EAC的中位线，∴BF＝AC．∵＝，∴＋＝＋，即＝，∴BD＝AC．∴BF＝BD．　(3)过点B作AE的垂线，与⊙O的交点即为所求的点P，‎ 则有PB⊥AE．理由如下：连结PG，PF．∵BF为△EAC的中位线，∴BF∥AC，∴∠FBE＝∠CAE．∵＝，∴∠CAB＝∠DBA．∴∠FBE＝∠DBA．∵PB⊥AE，∴∠PBA＝∠PBE＝90°．∴∠PBG＝∠PBF．∵G为BD的中点，∴BG＝BD．由(2)可知BF＝BD．∴BG＝BF．又∵∠PBG＝∠PBF，BP＝BP，∴△PBG≌△PBF(SAS)，∴PG＝PF．‎