中考复习———全等三角形平行四边形

中考复习———全等三角形平行四边形

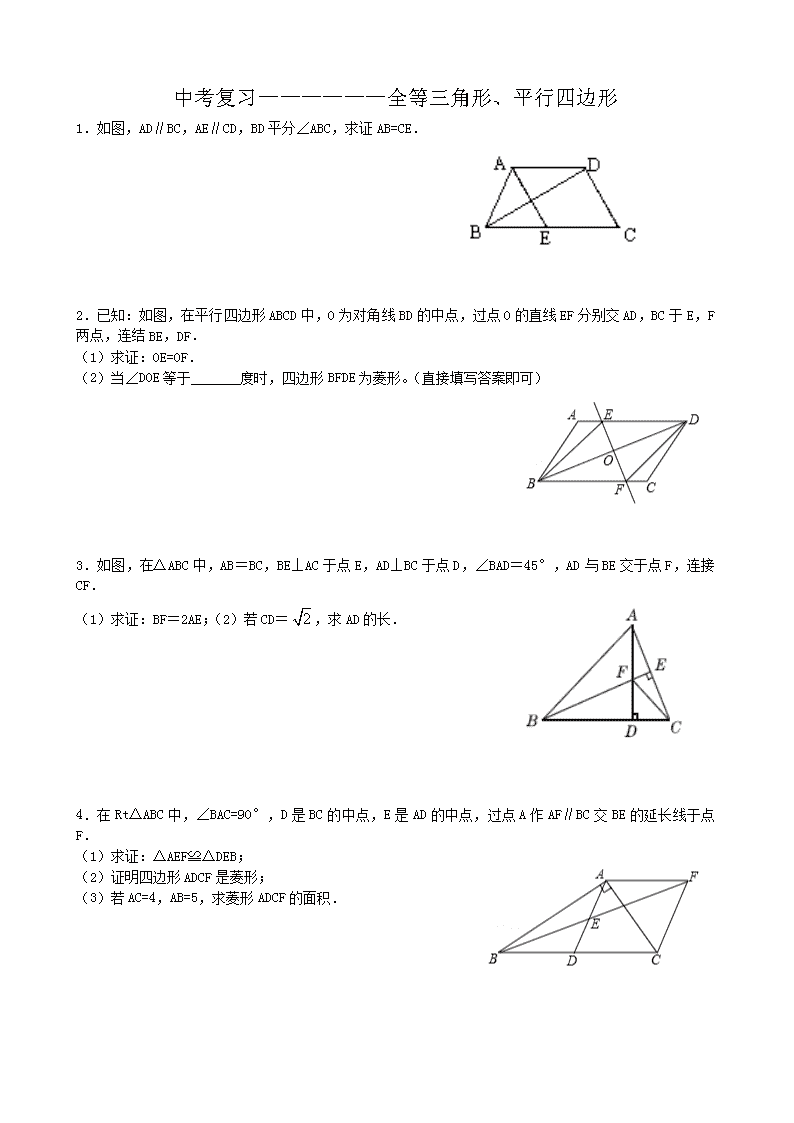
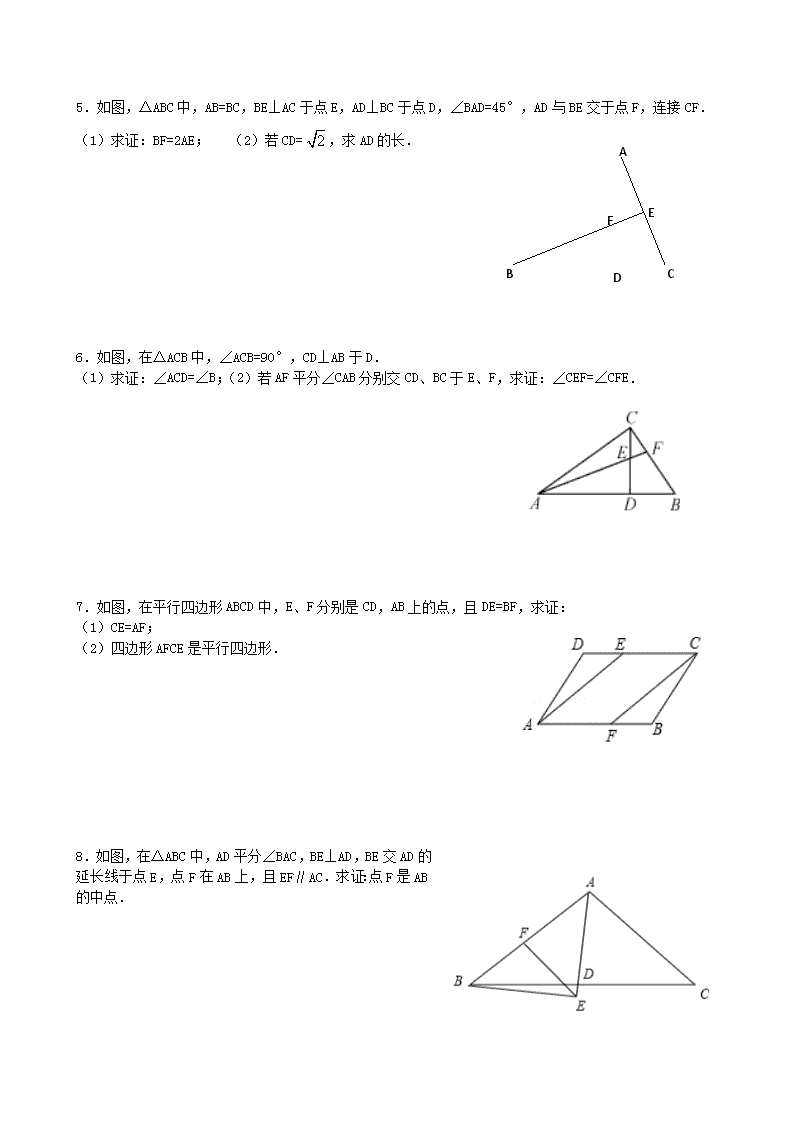
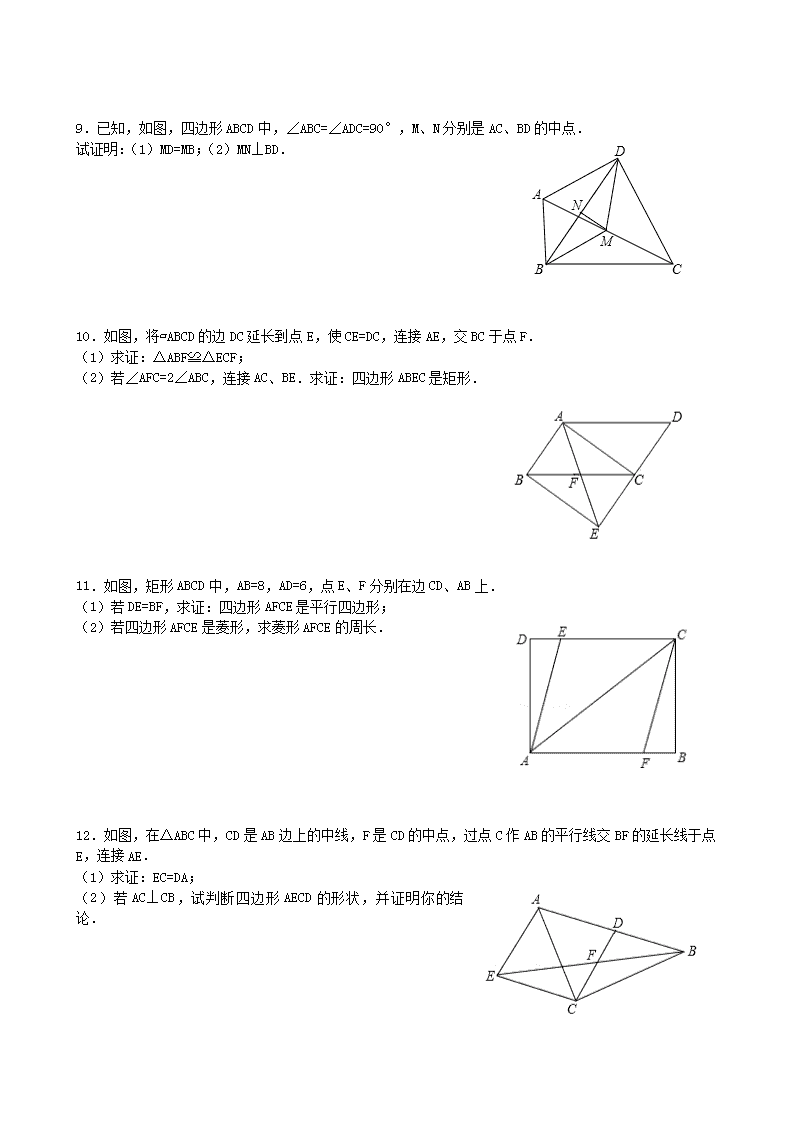
中考复习——————全等三角形、平行四边形 ‎1．如图，AD∥BC，AE∥CD，BD平分∠ABC，求证AB=CE．‎ ‎2．已知：如图，在平行四边形ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．‎ ‎（1）求证：OE=OF．‎ ‎（2）当∠DOE等于 度时，四边形BFDE为菱形。（直接填写答案即可）‎ ‎3．如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF．‎ ‎（1）求证：BF＝2AE；（2）若CD＝，求AD的长．‎ ‎4．在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．‎ ‎（1）求证：△AEF≌△DEB；‎ ‎（2）证明四边形ADCF是菱形；‎ ‎（3）若AC=4，AB=5，求菱形ADCF的面积．‎ A B C D F E ‎5．如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF．‎ ‎（1）求证：BF=2AE； （2）若CD=，求AD的长．‎ ‎6．如图，在△ACB中，∠ACB=90°，CD⊥AB于D．‎ ‎（1）求证：∠ACD=∠B；（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF=∠CFE．‎ ‎7．如图，在平行四边形ABCD中，E、F分别是CD，AB上的点，且DE=BF，求证：‎ ‎（1）CE=AF；‎ ‎（2）四边形AFCE是平行四边形．‎ ‎8．如图，在△ABC中，AD平分∠BAC，BE⊥AD，BE交AD的延长线于点E，点F在AB上，且EF∥AC．求证：点F是AB的中点．‎ ‎9．已知，如图，四边形ABCD中，∠ABC=∠ADC=90°，M、N分别是AC、BD的中点．‎ 试证明：（1）MD=MB；（2）MN⊥BD．‎ ‎10．如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．‎ ‎（1）求证：△ABF≌△ECF；‎ ‎（2）若∠AFC=2∠ABC，连接AC、BE．求证：四边形ABEC是矩形．‎ ‎11．如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．‎ ‎（1）若DE=BF，求证：四边形AFCE是平行四边形；‎ ‎（2）若四边形AFCE是菱形，求菱形AFCE的周长．‎ ‎12．如图，在△ABC中，CD是AB边上的中线，F是CD的中点，过点C作AB的平行线交BF的延长线于点E，连接AE．‎ ‎（1）求证：EC=DA；‎ ‎（2）若AC⊥CB，试判断四边形AECD的形状，并证明你的结论．‎ ‎13．如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．‎ ‎（1）PC=PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．‎ ‎14．如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．‎ ‎（1）求证：四边形OCED为矩形；‎ ‎（2）在BC上截取CF＝CO，连接OF，若AC＝16，BD＝12，求四边形OFCD的面积．‎ ‎15．将一矩形纸片OABC放在平面直角坐标系中，O（0，0），A（6，0），C（0，3）．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动秒时，动点P从点A出发以相等的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．‎ ‎（1）求点B的坐标，并用含t的代数式表示OP，OQ；‎ ‎（2）当t=1时，如图1，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处，求点D的坐标；‎ ‎（3）在（2）的条件下，矩形对角线AC,BO交于M,取OM中点G,BM中点H，求证当t=1时四边形DGPH是平行四边形．‎ 参考答案 ‎1．证明过程见解析．‎ ‎【解析】试题分析：根据题意得出四边形AECD为平行四边形，得到AD=CE，根据角平分线的性质以及平行线的性质得到AB=AD，从而得到AB=CE．‎ 试题解析：∵AD∥BC，AE∥CD ∴四边形AECD是平行四边形 ‎ ‎∴AD=CE又∵BD平分∠ABC ∴∠1=∠2 ∵AD∥EC ∴∠3=∠2∴∠1=∠3 ∴AB=AD ∴AB=CE 考点：（1）平行线的性质；（2）平行四边形的性质．‎ ‎2．（1）证明过程见解析；（2）90°．‎ ‎【解析】试题分析：（1）根据平行四边形的性质得出BO=DO，AD∥BC，则∠EDB=∠FBO，结合对顶角得出△DOE和△BOF全等，得到OE=OF；（2）根据对角线互相垂直的平行四边形为菱形得出答案．‎ 试题解析：（1）∵四边形ABCD是平行四边形，O为对角线BD的中点， ‎ ‎∴BO=DO，AD∥BC ‎∴∠EDB=∠FBO，在△EOD和△FOB中，∴△DOE≌△BOF（ASA）； ∴OE=OF ‎ ‎（2）当∠DOE= 90°时，四边形BFED为菱形，考点：（1）平行四边形的性质；（2）菱形的判定．‎ ‎3．（1）证明过程见解析；（2）AD=2+‎ ‎【解析】试题分析：（1）根据AD⊥BC，∠BAD=45°，得出AD=BD，∠ADC=∠FDB=90°，根据AD⊥BC，BE⊥AC得出∠CAD=∠CBE，从而得出△ADC和△BDF全等，得出AC=BF，根据AB=BC，BE⊥AC，得出AE=EC，可得BF=2AE；（2）根据△ADC和△BDF全等得出DF=CD=，根据Rt△CDF的勾股定理得出CF=2，得出AF=FC=2，根据AD=AF+DF求出长度．‎ 试题解析：（1）∵ AD⊥BC，∠BAD＝45°，∴ ∠ABD=∠BAD=45°．∴ AD=BD．∵ AD⊥BC,BE⊥AC, ‎ ‎∴ ∠CAD+∠ACD=90°，∠CBE+∠ACD＝90o ∴ ∠CAD=∠CBE．又∵ ∠CDA=∠FDB=90°，∴ △ADC≌△BDF． ‎ ‎∴ AC=BF． ∵ AB=BC,BE⊥AC, ∴ AE=EC，即AC＝2AE．∴ BF＝2AE．‎ ‎（2）∵ △ADC≌△BDF，∴ DF=CD=． ∴ 在Rt△CDF中，CF＝＝2．‎ ‎∵ BE⊥AC,AE=EC,∴ AF=FC=2． ∴ AD=AF+DF=2+． 考点：三角形全等的证明与性质．‎ ‎4．（1）见解析；（2）见解析；（3）10．‎ ‎【解析】试题分析：（1）根据AAS证△AFE≌△DBE；‎ ‎（2）利用①中全等三角形的对应边相等得到AF=BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形，由“直角三角形斜边的中线等于斜边的一半”得到AD=DC，从而得出结论；‎ ‎（3）由直角三角形ABC与菱形有相同的高，根据等积变形求出这个高，代入菱形面积公式可求出结论．‎ ‎（1）证明：①∵AF∥BC，∴∠AFE=∠DBE，∵E是AD的中点，AD是BC边上的中线，∴AE=DE，BD=CD，‎ 在△AFE和△DBE中，，∴△AFE≌△DBE（AAS）；‎ ‎（2）证明：由（1）知，△AFE≌△DBE，则AF=DB．∵DB=DC，∴AF=CD．∵AF∥BC，∴四边形ADCF是平行四边形，∵∠BAC=90°，D是BC的中点，E是AD的中点，∴AD=DC=BC，∴四边形ADCF是菱形；‎ ‎（3）解：设菱形DC边上的高为h，∴RT△ABC斜边BC边上的高也为h，∵BC==，‎ ‎∴DC=BC=，∴h==，菱形ADCF的面积为：DC•h=×=10．‎ 考点：菱形的判定与性质；全等三角形的判定与性质；直角三角形斜边上的中线；三角形中位线定理．‎ ‎5．（2）2+‎ ‎【解析】试题分析：（1）先判定出△ABD是等腰直角三角形，根据等腰直角三角形的性质可得AD=BD，再根据同角的余角相等求出∠CAD=∠CBE，然后利用“角边角”证明△ADC和△BDF全等，根据全等三角形对应边相等可得BF=AC，再根据等腰三角形三线合一的性质可得AC=2AF，从而得证；‎ ‎（2）根据全等三角形对应边相等可得DF=CD，然后利用勾股定理列式求出CF，再根据线段垂直平分线上的点到线段两端点的距离相等可得AF=CF，然后根据AD=AF+DF代入数据即可得解．‎ 试题解析：（1）证明：∵AD⊥BC，∠BAD=45°，∴△ABD是等腰直角三角形，∴AD=BD，∵BE⊥AC，AD⊥BC，‎ ‎∴∠CAD+∠ACD=90°，∠CBE+∠ACD=90°，∴∠CAD=∠CBE，在△ADC和△BDF中，，‎ ‎∴△ADC≌△BDF（ASA），∴BF=AC，∵AB=BC，BE⊥AC，∴AC=2AE，∴BF=2AE；‎ ‎（2）解：∵△ADC≌△BDF，∴DF=CD=，在Rt△CDF中，CF===2，‎ ‎∵BE⊥AC，AE=EC，∴AF=CF=2，∴AD=AF+DF=2+．考点：全等三角形的判定与性质，等腰直角三角形的判定与性质，等腰三角形三线合一的性质，勾股定理的应用，以及线段垂直平分线上的点到线段两端点的距离相的性质 ‎6．详见解析．‎ ‎【解析】试题分析：（1）由于∠ACD与∠B都是∠BCD的余角，根据同角的余角相等即可得∠ACD=∠B；（2）根据直角三角形两锐角互余得出∠CFA=90°-∠CAF，∠AED=90°-∠DAE，再根据角平分线的定义得出∠CAF=∠DAE，然后由对顶角相等的性质，等量代换即可证明∠CEF=∠CFE．‎ 试题解析：（1）∵∠ACB＝90°，CD⊥AB于D，∴∠ACD＋∠BCD＝90°，∠B＋∠BCD＝90°，‎ ‎∴∠ACD＝∠B．在Rt△AFC中，∠CFA＝90°－∠CAF，同理在Rt△AED中，∠AED＝90°－∠DAE．‎ 又∵AF平分∠CAB，∴∠CAF＝∠DAE，∴∠AED＝∠CFE，又∵∠CEF＝∠AED，∴∠CEF＝∠CFE．‎ 考点：同角的余角相等；直角三角形两锐角互余．‎ ‎7．(1)证明见解析,（2）证明见解析.‎ ‎【解析】试题分析：（1）根据平行四边形的对边相等得AB=CD，已知DE=BF，再作线段的差可得CE=AF；‎ ‎（2）利用CE与AF平行且相等，可证四边形AFCE是平行四边形．‎ 试题解析：（1）∵四边形ABCD为平行四边形，∴AB=CD．又∵DE=BF，∴AB-BF=CD-DE．即AF=CE．‎ ‎（2）∵AF=CE，AF∥CE，∴四边形AFCE是平行四边形．考点：平行四边形的判定．‎ ‎8．详见解析．‎ ‎【解析】试题分析：由AD为角平分线可得再由∠BAE=∠CAE，由EF∥AC，根据两直线平行内错角相等可得∠AEF=∠CAE，所以∠AEF=∠BAE，根据等角对等边即可得AF=EF．又因∠BAE+∠ABE=90°，∠BEF+∠AEF=90°，∠AEF=∠BAE，利用等角的余角相等可得出∠BEF=∠ABE，根据等角对等边得到即可得BF=EF，所以AF=BF，即F为AB的中点．‎ 试题解析：证明：∵AD平分∠BAC，∴∠BAE=∠CAE，∵EF∥AC，∴∠AEF=∠CAE，∴∠AEF=∠BAE，‎ ‎∴AF=EF，又∵BE⊥AD，∴∠BAE+∠ABE=90°，∠BEF+∠AEF=90°，又∠AEF=∠BAE，∴∠ABE=∠BEF，‎ ‎∴BF=EF，∴AF=BF，∴F为AB中点．考点：等腰三角形的判定与性质．‎ ‎9．（1）证明见试题解析；（2）证明见试题解析．‎ ‎【解析】‎ 试题分析：（1）根据直角三角形斜边上的中线等于斜边的一半，以及等边对等角的性质即可证明；‎ ‎（2）根据等腰三角形的三线合一证明．‎ 试题解析：（1）∵∠ABC=∠ADC=90°，M是AC的中点，∴BM=AC，DM=AC，∴DM=BM；‎ ‎（2）由（1）可知DM=BM，∵N是BD的中点，∴MN⊥BD．考点：1．直角三角形斜边上的中线；2．等腰三角形的判定与性质．‎ ‎10．（1）‎ ‎【解析】试题分析：（1）由四边形ABCD是平行四边形，CE=DC，易证得∠ABF=∠ECF，∠AFB=∠EFC，AB=EC，则可证得△ABF≌△ECF；‎ ‎（2）由△ABF≌△ECF，∠AFC=2∠ABC，即可证得∠ABC=∠BAF，继而证得AE=BC，又由AD=BC，则可得AE=AD，再利用等腰三角形三线合一的性质可得AC⊥ED，进而可得结论．‎ 试题解析：证明：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵EC=DC，∴AB=EC，‎ 在△ABF和△ECF中，∠ABF=∠ECF，∠AFB=∠EFC，AB=EC，∴△ABF≌△ECF（AAS）；‎ ‎（2）∵△ABF≌△ECF，∴AF=FE，BF=FC．∵∠AFC=2∠ABC，又∵∠AFC=∠ABC+∠BAF，∴∠ABC=∠BAF．‎ ‎∴AF=BF．∴AE=BC，又∵四边形ABCD为平行四边形，∴AD=BC．∴AE=AD．∵CE=DC，∴AC⊥ED，‎ ‎∴四边形ABEC是矩形．考点：矩形的判定；全等三角形的判定与性质；平行四边形的性质．‎ ‎11．（1）证明见试题解析；（2）25．‎ ‎【解析】试题分析：（1）由四边形ABCD为矩形，得到AB=CD，AB∥CD，由DE=BF，得到AF=CE，AF∥CE，即可证明四边形AFCE是平行四边形；‎ ‎（2）由四边形AFCE是菱形，得到AE=CE，然后设DE=x，表示出AE，CE的长度，根据相等求出x的值，继而可求得菱形的边长及周长．‎ 试题解析；（1）∵四边形ABCD为矩形，∴AB=CD，AB∥CD，∵DE=BF，∴AF=CE，AF∥CE，∴四边形AFCE是平行四边形；‎ ‎（2）∵四边形AFCE是菱形，∴AE=CE，设DE=x，则AE=，CE=8﹣x，则，解得：x=，则菱形的边长为：=，周长为：4×=25，故菱形AFCE的周长为25．‎ 考点：1．矩形的性质；2．平行四边形的判定；3．菱形的性质．‎ ‎12．（1）证明见试题解析；（2）四边形AECD是菱形．‎ ‎【解析】试题分析：（1）由EC∥AB，得出∠FEC=∠DBF，∠ECF=∠BDF，由F是CD的中点，得出FD=CF，再利用AAS证明△FEC≌△DBF，从而可以得到结论；‎ ‎（2）利用直角三角形的性质：斜边上的中线等于斜边的一半，得出CD=DA，进一步得出结论即可．‎ 试题解析：（1）∵EC∥AB，∴∠FEC=∠DBF，∠ECF=∠BDF，∵F是CD的中点，∴FD=CF，在△FEC与△DBF中，∵∠FEC=∠DBF，∠ECF∠BDF，FD=CF，∴△FEC≌△DBF，∴EC=BD，又∵CD是AB边上的中线，∴BD=AD，∴EC=AD；‎ ‎（2）四边形AECD是菱形．证明如下：‎ ‎∵EC=AD，EC∥AD，∴四边形AECD是平行四边形，∵AC⊥CB，CD是AB边上的中线，∴CD=AD=BD，∴四边形AECD是菱形．‎ 考点：1．全等三角形的判定与性质；2．菱形的判定．‎ ‎13．（1）证明见试题解析；（2）90°；（3）AP=CE．‎ ‎【解析】‎ 试题分析：（1）先证出△ABP≌△CBP，得到PA=PC，由PA=PE，得到PC=PE；‎ ‎（2）由△ABP≌△CBP，得到∠BAP=∠BCP，进而得到∠DAP=∠DCP，由PA=PC，得到∠DAP=∠E，∠DCP=∠E，最后∠CPF=∠EDF=90°得到结论；‎ ‎（3）借助（1）和（2）的证明方法容易证明结论．‎ 试题解析：（1）在正方形ABCD中，AB=BC，∠ABP=∠CBP=45°，在△ABP和△CBP中，∵AB=BC，∠ABP=∠‎ CBP，PB=PB，∴△ABP≌△CBP（SAS），∴PA=PC，∵PA=PE，∴PC=PE；‎ ‎（2）由（1）知，△ABP≌△CBP，∴∠BAP=∠BCP，∴∠DAP=∠DCP，∵PA=PC，∴∠DAP=∠E，∴∠DCP=∠E，∵∠CFP=∠EFD（对顶角相等），∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E，即∠CPF=∠EDF=90°；‎ ‎（3）在正方形ABCD中，AB=BC，∠ABP=∠CBP=45°，在△ABP和△CBP中，∵AB=BC，∠ABP=∠CBP，PB=PB，∴△ABP≌△CBP（SAS），∴PA=PC，∠BAP=∠BCP，∵PA=PE，∴PC=PE，∴∠DAP=∠DCP，∵PA=PC，∴∠DAP=∠E，∴∠DCP=∠E，∵∠CFP=∠EFD（对顶角相等），∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E，即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°，∴△EPC是等边三角形，∴PC=CE，∴AP=CE．‎ 考点：1．正方形的性质；2．全等三角形的判定与性质；3．菱形的性质；4．探究型；5．综合题；6．压轴题．‎ ‎14．（1）证明见解析；（2）．‎ ‎【解析】‎ 试题分析：（1）由DE∥AC，CE∥BD可得四边形OCED为平行四边形，又AC⊥BD从而得四边形OCED为矩形；‎ ‎（2）过点O作OH⊥BC，垂足为H，由已知可得三角形OBC、OCD的面积，BC的长，由面积法可得OH的长，从而可得三角形OCF的面积，三角形OCD与三角形OCF的和即为所求．‎ 试题解析：（1）∵DE∥AC，CE∥BD，∴四边形OCED为平行四边形．又∵四边形ABCD是菱形，∴AC⊥BD．∴∠DOC=90°．∴四边形OCED为矩形．‎ ‎（2）∵菱形ABCD，∴AC与BD互相垂直平分于点O，∴OD＝OB＝BD＝6，OA＝OC＝AC＝8，∴CF=CO=8，S△BOC=S△DOC＝＝24，在Rt△OBC中，BC＝＝10，．作OH⊥BC于点H，则有BC·OH=24，∴OH=，∴S△COF=CF·OH=．∴S四边形OFCD＝S△DOC＋S△OCF＝；‎ 考点：1．菱形的性质；2．平行四边形的判定；3．矩形的判定．‎ ‎15．（1）B（6,3）；OP=6－t；OQ=+t；（2）D（1,3）；（3）见解析．‎ ‎【解析】‎ 试题分析：（1）根据矩形的性质求出点B的坐标，根据动点问题求出OP和OQ的长度；（2）根据折叠图形的性质求出OQ和DQ的长度，然后根据勾股定理求出CD的长度，得到点D的坐标；（3）根据一组对边平行且相等的四边形为平行四边形进行判定．‎ 试题解析：（1）B（6,3）；OP=OA-AP=6-t, OQ=+t．‎ ‎（2）当t=1时，OP=5，OQ=,则CQ=3-=，由折叠可知：△OPQ≌△DPQ, ∴OQ=DQ=‎ 由勾股定理,得：CD=1 ∴D（1,3） ‎ ‎（3）∵四边形OABC是矩形，∴OA=BC, 又∵CD=AP=1， ∴BC-CD=OA-AP,即BD=OP,‎ ‎∵ OM=MB,G为OM中点，H为BM中点 , ∴OG=BH, ∵OA∥BC ∴∠1=∠2‎ 在△POG和△DBH中，OG=BH，∠1=∠2，OP=DB ∴△POG≌△DBH ∴∠OGP=∠BHD PG=DH ‎∴∠MGP=∠DHM ∴PG∥DH 又∵PG=DH ∴四边形DGPH是平行四边形．．．‎ 考点：折叠图形的性质、平行四边形的判定、三角形全等的判定与性质．‎