四川省绵阳中考数学模拟试题含答案

四川省绵阳中考数学模拟试题含答案

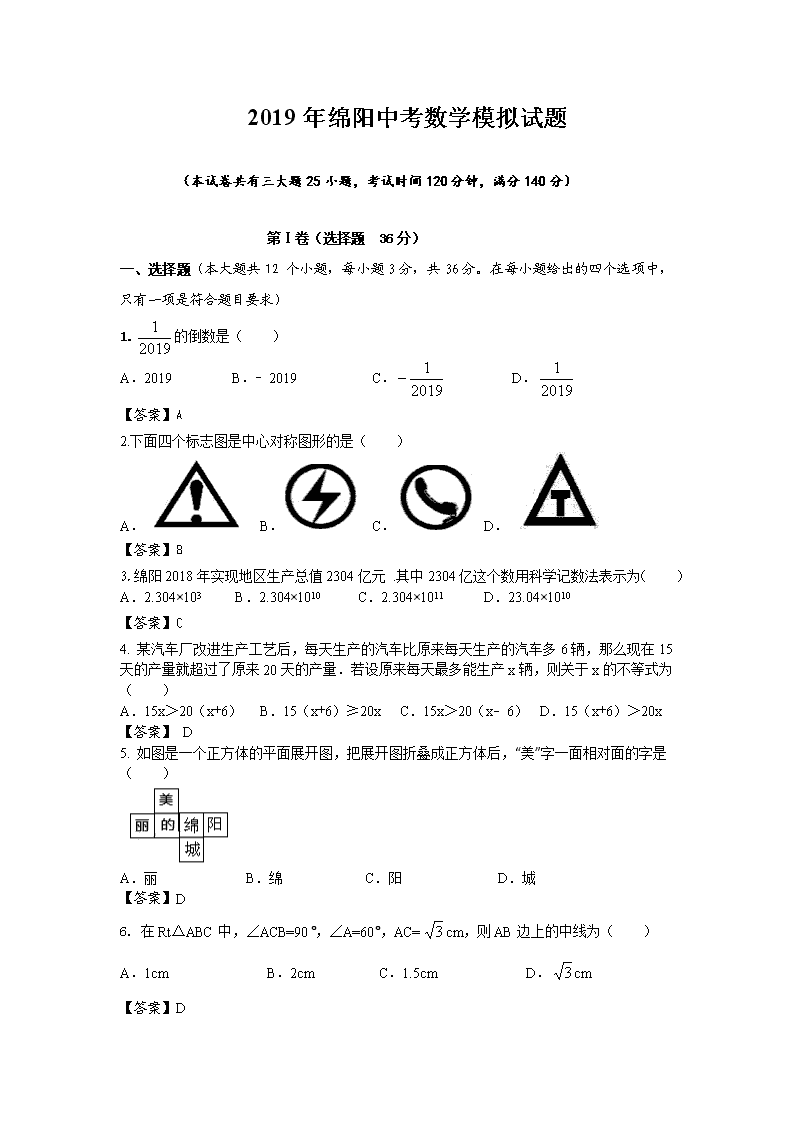
‎ 2019年绵阳中考数学模拟试题 ‎（本试卷共有三大题25小题，考试时间120分钟，满分140分）‎ ‎ 第Ⅰ卷（选择题 36分）‎ 一、选择题（本大题共12 个小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求）‎ ‎1.的倒数是（　　）‎ A．2019 B．﹣2019 C． D．‎ ‎【答案】A ‎2.下面四个标志图是中心对称图形的是（　　）‎ A． B． C． D． ‎ ‎【答案】B ‎3.绵阳2018年实现地区生产总值2304亿元 .其中2304亿这个数用科学记数法表示为（　　）‎ A．2.304×103 B．2.304×1010 C．2.304×1011 D．23.04×1010‎ ‎【答案】C ‎4. 某汽车厂改进生产工艺后，每天生产的汽车比原来每天生产的汽车多6辆，那么现在15天的产量就超过了原来20天的产量．若设原来每天最多能生产x辆，则关于x的不等式为（　　）‎ A．15x＞20（x+6） B．15（x+6）≥20x C．15x＞20（x﹣6） D．15（x+6）＞20x ‎【答案】 D ‎5. 如图是一个正方体的平面展开图，把展开图折叠成正方体后，“美”字一面相对面的字是（　　）‎ A．丽 B．绵 C．阳 D．城 ‎【答案】D ‎6. 在Rt△ABC中，∠ACB=90°，∠A=60°，AC=cm，则AB边上的中线为（　　）‎ A．1cm B．2cm C．1.5cm D．cm ‎【答案】D ‎7. 如图，DE∥BC，∠D=2∠DBC，∠1=∠2，则∠DEB的度数为（　　）‎ A．30° B．45° C．60° D．无法计算 ‎【答案】A ‎8. 若将点P（1，﹣m）向右平移2个单位后，再向上平移1个单位得到点Q（n，3），则点（m，n）的坐标为（　　）‎ A．（3，﹣2） B．（2，﹣3） C．（3，2） D．（﹣2，3）‎ ‎【答案】D ‎9. 从三个方向看到一几何体的图形如图所示，则这个几何体中小正方体的个数有（　　）‎ A．4个 B．5个 C．6个 D．7个 ‎【答案】B ‎10. 一个质地均匀的正方形骰子的六个面上分别有1到6的点数，将骰子抛掷两次，抛第一次将朝上一面的点数记为x．抛第二次，将朝上一面的点数记为y，则点（x，y）落在直线y=﹣2x+8上的概率为（　　）‎ A． B． C． D．‎ ‎【答案】B ‎11. 如图，小明要测量河内小岛B到河边公路l的距离，在A点测得∠BAD=30°，在C点测得∠BCD=60°，又测得AC=60米，则小岛B到公路l的距离为（　　）‎ A．30米 B．30米 C．40米 D．（30+30）米 ‎【答案】B ‎12. 将正奇数按下表排成5列：‎ 第一列 第二列 第三列 第四列 第五列 第1行 ‎1‎ ‎3‎ ‎5‎ ‎7‎ 第2行 ‎15‎ ‎13‎ ‎11‎ ‎9‎ 第3行 ‎17‎ ‎19‎ ‎21‎ ‎23‎ 第4行 ‎ ‎31‎ ‎29‎ ‎27‎ ‎25‎ ‎…‎ 根据上面规律，2019应在（　　）‎ A．第252行第2列 B．第253行第1列 C．第253行第2列 D．第253行第3列 ‎【答案】D 第Ⅱ卷（非选择题 共104分）‎ 二、 填空题（本大题共6个小题，每小题3分，共18分.把答案填写在题中横线上）‎ ‎13.计算：=　 　．‎ ‎【答案】-4‎ ‎14. 函数y=，其中x的取值范围是　 　．‎ ‎【答案】x≠3‎ ‎15. 如图所示，在菱形ABCD中，AB=2，∠BAD=120°，M为BC上一点，N为CD上一点，∠MAN=60°，则四边形AMCN的面积为　　 ．‎ ‎【答案】‎ ‎16. 如图，AB是⊙0的直径，C、D是AB上的三等分点，如果⊙O的半径为l，P是线段AB上的任意一点，则图中阴影部分的面积为　　 ．‎ ‎【答案】‎ ‎17. 已知a、b为不等的两个实数，且a2﹣3a﹣2020=0，b2﹣3b﹣2020=0，则a2﹣2a+b=　 　．‎ ‎【答案】2023‎ ‎18. 如图，D为正三角形ABC内一点，BD=5，CD=3，∠ADC=150°，则AD的长为　 　．‎ ‎【答案】4‎ ‎ 三、 解答题（本大题共7个小题，共86分。解答题应写出文字说明、证明过程或演算步骤）‎ ‎19.（每小题8分，共16分）‎ ‎（1）计算：（）﹣1+|1﹣|﹣tan30°．‎ ‎【解答】解：原式=4+﹣1﹣3×……………………6分 ‎ =4+﹣1﹣3=．……………………………………8分 ‎（2）化简：‎ ‎【解答】解：原式=……………………6分 ‎ ==…………………………8分 ‎20.（11分）随着城市化进程的发展，农村留守儿童问题已引起全社会的广泛关注，为了了解某农村初中800名学生监护人的情况，我们从中抽取一部分学生作为样本进行数据处理，得到如下的分布表和条形统计图：‎ 监护人 频数 频率 祖辈照顾 ‎　 　 ‎ ‎0.30‎ 亲朋好友 ‎13‎ ‎0.13‎ 母亲一人在家 ‎34‎ ‎　 　‎ 父亲一人在家 ‎　　 ‎ ‎　 　‎ 父母都在家 ‎13‎ ‎0.13‎ ‎（1）此次参加调查共有 人.‎ ‎（2）根据上述数据，补全统计表和条形统计图；‎ ‎（3）若全市共有40000名农村初中学生，试估计该市初中生的监护人不是自己父亲或母亲的共有多少名？‎ ‎【解答】解：（1）总人数=13÷0.13=100人；……………………2分 ‎（2）补全图表如下：‎ 监护人 频数 频率 祖辈照顾 ‎30‎ ‎0.30‎ 亲朋好友 ‎13‎ ‎0.13‎ 母亲一人在家 ‎34‎ ‎0.34‎ 父亲一人在家 ‎10‎ ‎0.10‎ 父母都在家 ‎13‎ ‎0.13‎ ‎………………………………………………………………………………………………6分 ‎……………………………………8分 ‎（2）∵不是父亲或母亲监护的频率分别为0.3和0.13，‎ ‎∴监护人不是自己父亲或母亲的共有40000×（0.3+0.13）=17200人………………11分 ‎21.（11分）已知，如图，AB是⊙O的直径，点E是弧AD的中点，连接BE交AC于点G，BG的垂直平分线CF交BG于H交AB于F点．‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）若AB=8，BC=6，求BE的长．‎ ‎【解题过程】（1）证明：连接AE，‎ ‎∵C在BG的垂直平分线CF上，∴CB=CG，∴∠1=∠2，…………………………1分 ‎∵AB是⊙O的直径，∴∠E=90°，∴∠3+∠4=90°，…………………………2分 ‎∵∠3=∠1=∠2，∴∠2+∠4=90°，…………………………3分 ‎∵点E是弧AD的中点，∴∠ABE=∠4，‎ ‎∴∠2+∠ABE=90°，即∠ABC=90°，…………………………4分 ‎∵OB是半径，‎ ‎∴BC是⊙O的切线；…………………………5分 ‎（2）解：∵BC是⊙O的切线，∴∠ABC=90°，‎ 由勾股定理，可得 AC==10，…………………………………………6分 ‎∵CG=CB=6，∴AG=10﹣6=4，‎ ‎∵∠E=∠E，∠4=∠ABE，‎ ‎∴△AEG∽△BEA，………………………………………………………………8分 ‎∴，‎ 设AE=x，BE=2x．‎ 在Rt△AEB中，由勾股定理，可得 x2+（2x）2=82．解得：x=，‎ ‎∴BE=2x=．……………………………………………………………………11分 ‎22.（11分）如图，在平面直角坐标系中，直线y=﹣x+6与x轴、y轴的正半轴分别相交于点A，B两点，点D在反比例函数y=（k＞0）的图象上，DA⊥OA，点P在y轴负半轴上，OP=14．‎ ‎（1）求线段PB的长；‎ ‎（2）当∠PDB=90°时，求反比例函数的解析式．‎ ‎【解题过程】解：（1）直线y=﹣x+6与x轴的交点A的坐标为（8，0），与y轴的交点坐标为（0，6），……………………………………………………………………2分 ‎∴OA=8，OB=6，∴PB=OP+OB=20；………………………………………………4分 ‎（2）作DE⊥OB于E，‎ ‎∵点A的坐标为（8，0），点D在反比例函数y=（k＞0）的图象上，DA⊥OA，‎ ‎∴DE=OA=8，OE=AD=，……………………………………………………6分 ‎∵∠PDB=90°，DE⊥OB，∴△DBE∽△PDE，‎ ‎∴，即82=（6﹣）×（14+），……………………………………8分 整理得，k2+64k﹣1280=0，‎ 解得，k1=16，k2=﹣80（舍去），‎ ‎∴反比例函数的解析式为y=．…………………………………………………11分 ‎23.（11分）绵阳市某汽车经销商根据市场需求，计划购进某品牌A、B两种型号的汽车共50辆，且A、B两种型号的汽车的进价分别为12万元和15万元，如果A型号的汽车加价15%，B型号的汽车加价16%出售．‎ ‎（1）求出该经销商所购汽车均全部售出的利润y（万元）与购进A种型号的汽车x（辆）之间的函数关系；‎ ‎（2）如果该经销商计划购进A、B两种型号的汽车所用资金不超过650万元，且A种型号的汽车不多于36辆，那么有几种购买方案？该经销商使用哪种方案可获得最大利润？最大利润是多少？‎ ‎【解题过程】解：（1）y=x×12×15%+（50-x）×15×16%=-0.6x+120…………3分 ‎（2），解得，………………………………6分 x的整数解有：34，35，36，因此，有三种购买方案：‎ 第一种方案：购买A型号的汽车34辆，B型号的汽车16辆；‎ 第二种方案：购买A型号的汽车35辆，B型号的汽车15辆；‎ 第三种方案：购买A型号的汽车36辆，B型号的汽车14辆．………………………9分 ‎∵y=-0.6x+120，k<0，∴y随着x的增加而减小，‎ ‎∴x=34时，y最大，最大值是99.6‎ ‎∴经销商使用方案一可获得最大利润，最大利润是99.6万元．………………………11分 ‎24.（12分）如图，已知在矩形ABCD中，BC=2CD=2a，点E在边CD上，在矩形ABCD的左侧作矩形ECGF，使CG=2GF=2b，连接BD，CF，连结AF交BD于点H．‎ ‎（1）求证：BD∥CF；‎ ‎（2）求证：H是AF的中点；‎ ‎（3）连结CH，若HC⊥BD，求a：b的值．‎ ‎【解题过程】解：（1）∵四边形ABCD、四边形ECGF均为矩形，‎ ‎∴∠G=∠DCB=90°，‎ ‎∵BC=2CD=2a，CG=2GF=2b，‎ ‎∴，‎ ‎∴△FGC∽△DCB，……………………………………………………………………3分 ‎∴∠FCG=∠DBC，‎ ‎∴BD∥CF．………………………………………………………………………………4分 ‎（2）如图1所示：连接AC，交BD于点O．‎ ‎∵四边形ABCD为矩形，∴OC=OA．……………………………………………………5分 又∵FC∥BD，∴HF：AH=OC：OA，∴HF=AH，‎ ‎∴点H是AF的中点．……………………………………………………………………7分 ‎（3）如图2所示：连接CH，CA，AC与BD交于点O．‎ 由勾股定理可知：FC=，AC=．……………8分 ‎∵四边形ABCD为矩形，‎ ‎∴DB=AC=，CO=AC=．……………………………………………………9分 ‎∵HO是△AFC的中位线，‎ ‎∴HO=FC=．‎ ‎∵S△DCB=DC×BC=DB×CH，‎ ‎∴CH=．………………………………………………………………10分 在△COH中，由勾股定理可知：HO2+CH2=OC2，即（）2+（）2=（）2．‎ 整理得：a2=．‎ ‎∴a：b=．………………………………………………………………………………12分 ‎25.（14分）如图，抛物线y=﹣x2+bx+c与x轴交于点A、C，与y轴交于点B，它的顶点是D，对称轴是直线x=﹣2，且OB=OC．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点P在上述抛物线上的对称轴上，且△ABP周长最小，求点P的坐标；‎ ‎（3）点E在直角坐标平面内，点B、C、D、E是一个平行四边形的四个顶点，求点E的坐标．‎ ‎【解题过程】解：（1）∵抛物线y=﹣x2+bx+c，对称轴是直线x=﹣2，‎ ‎∴，得b=﹣4，………………………………………………1分 ‎∵抛物线y=﹣x2+bx+c与x轴交于点A、C，与y轴交于点B，它的顶点是D，且OB=OC，‎ ‎∴点B的坐标为（0，c），点C的坐标为（﹣c，0），‎ ‎∴0=﹣（﹣c）2﹣4×（﹣c）+c，……………………………………………………3分 解得c=0（舍去）或c=5，‎ ‎∴抛物线的解析式是y=﹣x2﹣4x+5．………………………………………………4分 ‎（2）∵抛物线的解析式是y=﹣x2﹣4x+5=﹣（x+2）2+9，‎ ‎∴点D的坐标为（﹣2，9）．对称轴为x=-2…………………………………………5分 令x=0，y=5，即点B（0，5）；‎ 令y=0，﹣x2﹣4x+5=0，解得x=﹣5，或x=1，‎ 即点C（﹣5，0），点A（1，0）．……………………………………………………6分 设直线BC的解析式为y=kx+5．‎ ‎∵点C（﹣5，0）在直线BC上，‎ ‎∴0=﹣5k+5，解得：k=1，‎ 即直线BC的解析式为y=x+5．…………………………………………………………7分 当x=-2时，y=-2+5=3，故BC与对称轴的交点为（-2，3）‎ 由点A、点C关于抛物线的对称轴对称，则BC与对称轴的交点为P时，PA+PB最小，而AB不变，故△ABP周长最小；‎ ‎∴△ABP周长最小时，点P的坐标为（-2，3）…………………………………………8分 ‎（3）点E在直角坐标平面内，点B、C、D、E是一个平行四边形的四个顶点分三种情况：‎ ‎①以CD为对角线时，如图1所示．‎ 令线段CD的中点为F，由平行四边形的性质可知：‎ 点F为CD的中点，点F还是BE的中点．‎ ‎∵点C（﹣5，0），点D（﹣2，9），‎ ‎∴xF=，yF=，‎ ‎∴点F坐标为（﹣，），‎ ‎∵点B（0，5），‎ ‎∴xE=2×（﹣）﹣0=﹣7，yE=2×﹣5=4，‎ 即此时点E的坐标为（﹣7，4）；…………………………………………………………10分 ‎②以BC为对角线，如图2所示．‎ 令线段BC的中点为F，由平行四边形的性质可知：‎ 点F为BC的中点，点F还是DE的中点．‎ ‎∵点B（0，5），点C（﹣5，0），‎ ‎∴xF=，yF=，‎ ‎∴点F的坐标为（﹣，），‎ ‎∵点D（﹣2，9），‎ ‎∴xE=2×（﹣）﹣（﹣2）=﹣3，yE=2×﹣9=﹣4，‎ 即此时点E的坐标为（﹣3，﹣4）；……………………………………………………12分 ‎③以BD为对角线，如图3所示．‎ ‎ ‎ 令线段BD的中点为F，由平行四边形的性质可知：‎ 点F为BD的中点，点F还是CE的中点．‎ ‎∵点B（0，5），点D（﹣2，9），‎ ‎∴xF=，yF=，‎ ‎∴点F的坐标为（﹣1，7），‎ ‎∵点C（﹣5，0），‎ ‎∴xE=2×（﹣1）﹣（﹣5）=3，yE=2×7﹣0=14，‎ 即此时点E的坐标为（3，14）．……………………………………………………14分 综上可知：满足条件的点E的坐标为：（﹣7，4）、（﹣3，﹣4）和（3，14）．‎