- 2021-05-10 发布 |
- 37.5 KB |
- 5页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学专题18三级训练配答案
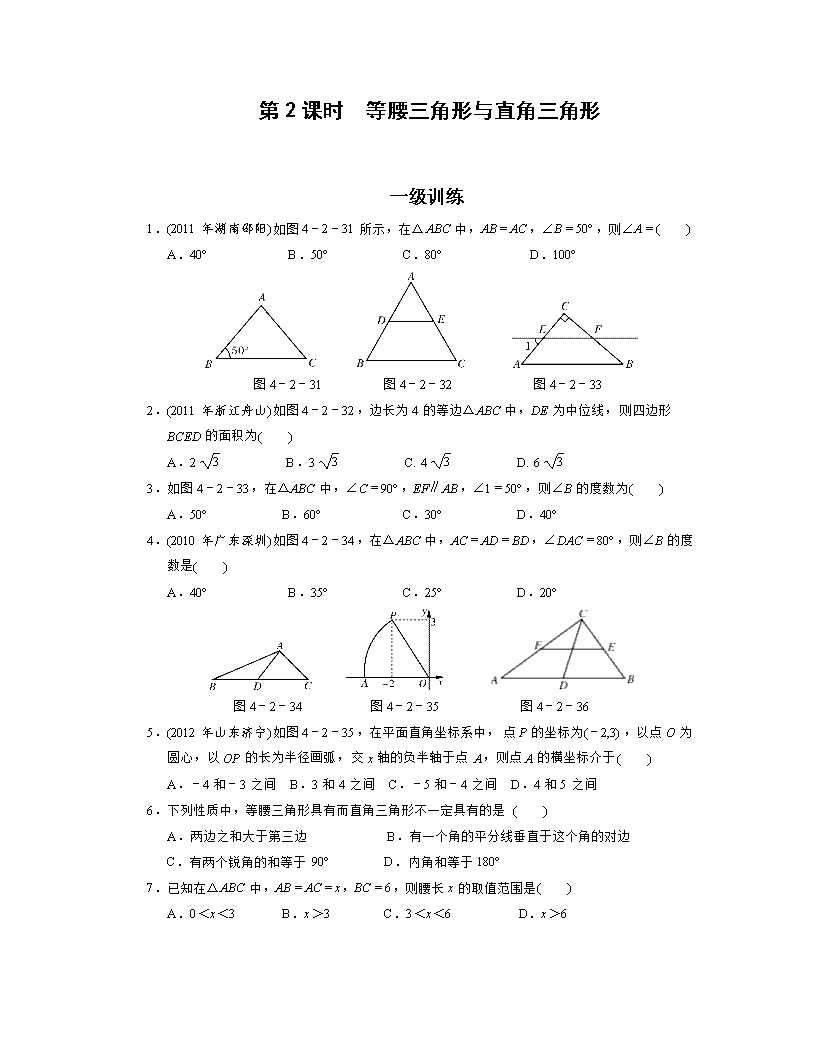
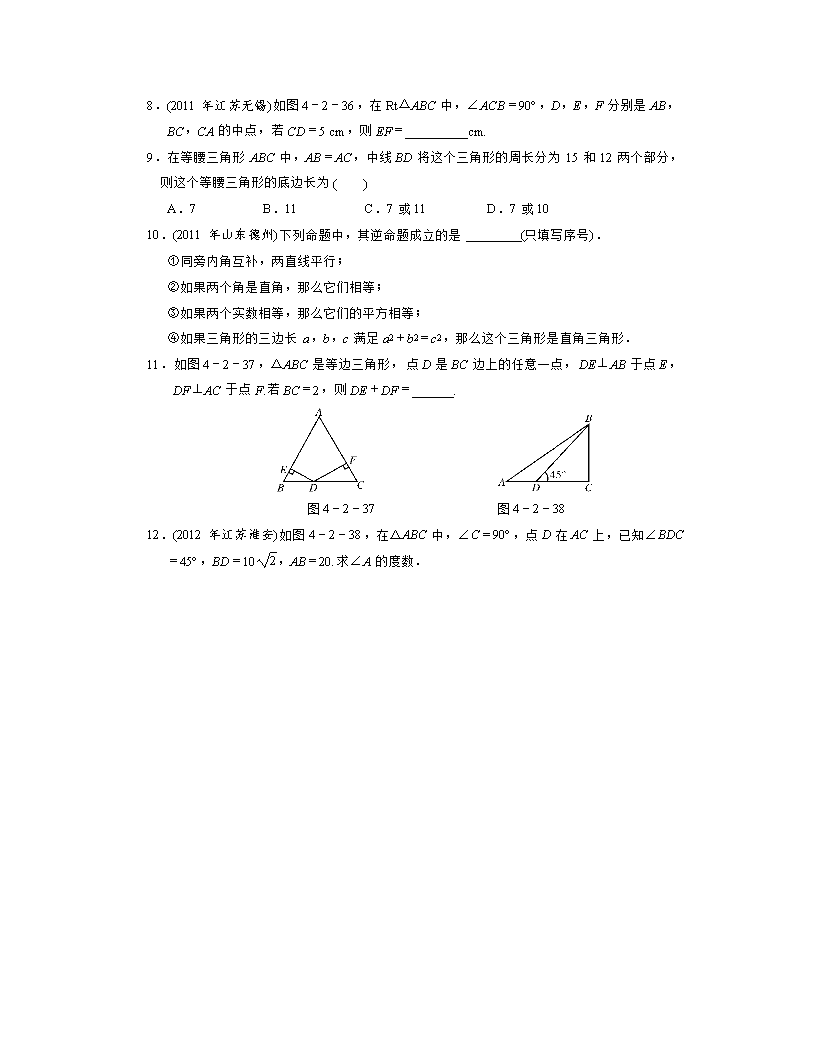
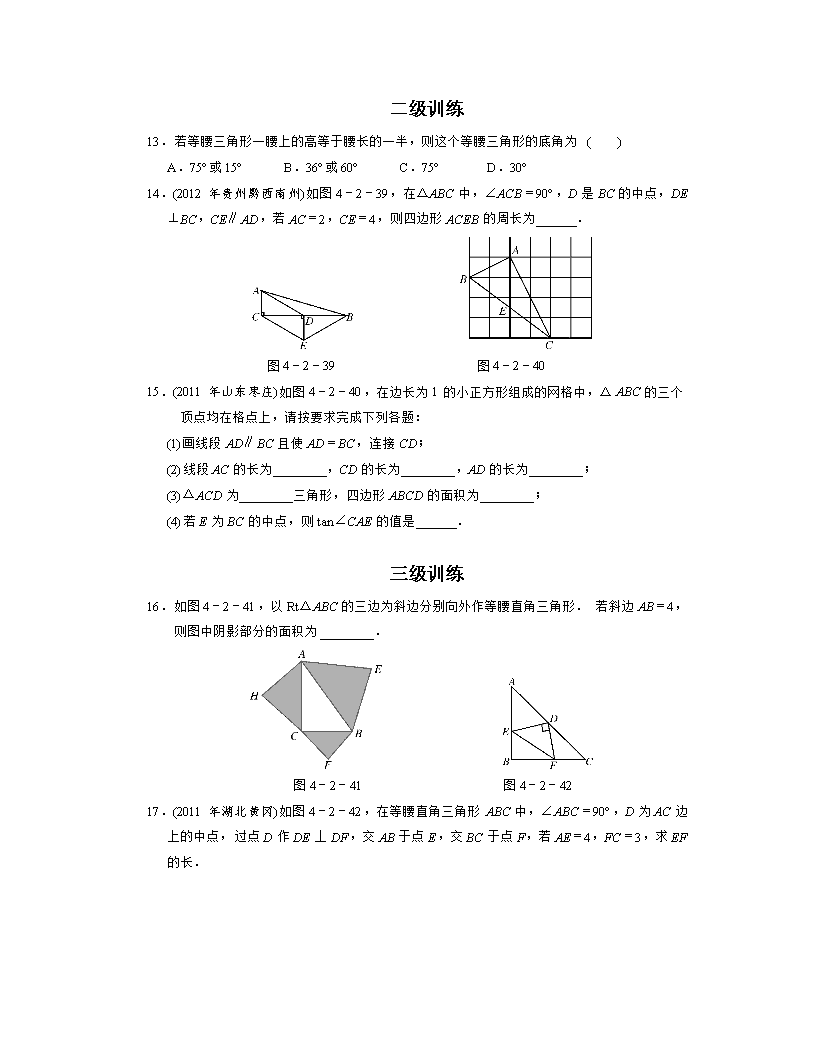
第2课时 等腰三角形与直角三角形 一级训练 1.(2011年湖南邵阳)如图4-2-31所示,在△ABC中,AB=AC,∠B=50°,则∠A=( ) A.40° B.50° C.80° D.100° 图4-2-31 图4-2-32 图4-2-33 2.(2011年浙江舟山)如图4-2-32,边长为4的等边△ABC中,DE为中位线,则四边形BCED的面积为( ) A.2 B.3 C. 4 D. 6 3.如图4-2-33,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( ) A.50° B.60° C.30° D.40° 4.(2010年广东深圳)如图4-2-34,在△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( ) A.40° B.35° C.25° D.20° 图4-2-34 图4-2-35 图4-2-36 5.(2012年山东济宁)如图4-2-35,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( ) A.-4和-3之间 B.3和4之间 C.-5和-4之间 D.4和5之间 6.下列性质中,等腰三角形具有而直角三角形不一定具有的是( ) A.两边之和大于第三边 B.有一个角的平分线垂直于这个角的对边 C.有两个锐角的和等于90° D.内角和等于180° 7.已知在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是( ) A.0<x<3 B.x>3 C.3<x<6 D.x>6 8.(2011年江苏无锡)如图4-2-36,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,CA的中点,若CD=5 cm,则EF=_________cm. 9.在等腰三角形ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( ) A.7 B.11 C.7或11 D.7或10 10.(2011年山东德州)下列命题中,其逆命题成立的是________(只填写序号). ①同旁内角互补,两直线平行; ②如果两个角是直角,那么它们相等; ③如果两个实数相等,那么它们的平方相等; ④如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形. 11.如图4-2-37,△ABC是等边三角形,点D是BC边上的任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=______. 图4-2-37 图4-2-38 12.(2012年江苏淮安)如图4-2-38,在△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,BD=10,AB=20.求∠A的度数. 二级训练 13.若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为( ) A.75°或15° B.36°或60° C.75° D.30° 14.(2012年贵州黔西南州)如图4-2-39,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为______. 图4-2-39 图4-2-40 15.(2011年山东枣庄)如图4-2-40,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: (1)画线段AD∥BC且使AD=BC,连接CD; (2)线段AC的长为________,CD的长为________,AD的长为________; (3)△ACD为________三角形,四边形ABCD的面积为________; (4)若E为BC的中点,则tan∠CAE的值是______. 三级训练 16.如图4-2-41,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=4,则图中阴影部分的面积为________. 图4-2-41 图4-2-42 17.(2011年湖北黄冈)如图4-2-42,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过点D作DE丄DF,交AB于点E,交BC于点F,若AE=4,FC=3,求EF的长. 参考答案 1.C 2.B 3.D 4.C 5.A 6.B 7.B 8.5 9.C 10.①④ 11. 12.解:∵在直角三角形BDC中, ∠BDC=45°,BD= 10, ∴BC=CD=10 . 又∵∠C=90°,AB=20, ∴∠A=30°. 13.A 解析:三角形的高可在三角形内、三角形外,于是可得等腰三角形的顶角为30°或150°,故底角为75°或15°. 14.10+2 15.解:(1)如图D11. 图D11 (2)2 5 (3)直角 10 (4) 16.8 17.解:连接BD,如图D12. 图D12 ∵在等腰直角三角形ABC中,D为AC边上的中点, ∴BD⊥AC,BD=CD=AD,∠ABD=45°. ∴∠C=45°.∴∠ABD=∠C. 又∵DE⊥DF, ∴∠FDC+∠BDF=∠EDB+∠BDF. ∴∠FDC=∠EDB. 在△EDB与△FDC中, ∵ ∴△EDB≌△FDC(ASA). ∴BE=FC=3. ∴AB=7,则BC=7. ∴BF=4. 在RT△EBF中, EF2=BE2+BF2=32+42, ∴EF=5.查看更多