最新最全全国各地1份中考数学试卷分类汇编动态问题

最新最全全国各地1份中考数学试卷分类汇编动态问题

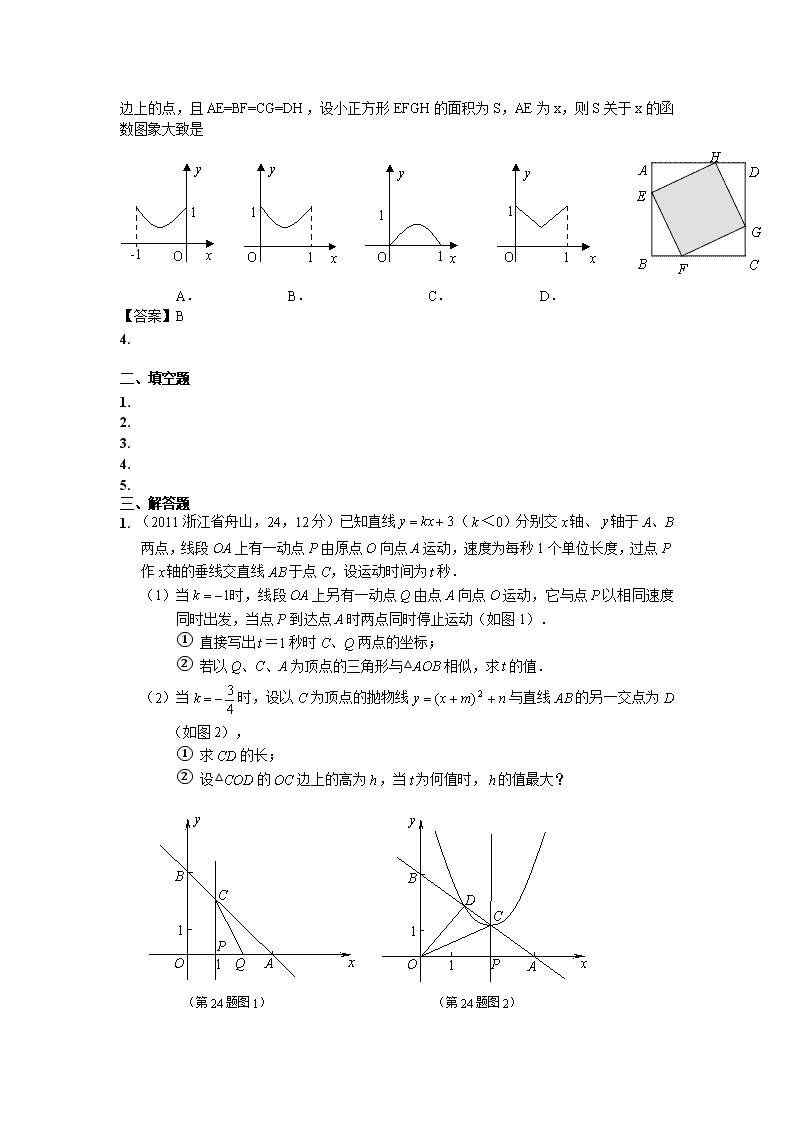
‎2011年全国各地100份中考数学试卷分类汇编 第44章 动态问题 一、选择题 ‎1. （2011安徽，10，4分）如图所示，P是菱形ABCD的对角线AC上一动点，过P垂直于AC的直线交菱形ABCD的边于M、N两点，设AC=2，BD=1，AP=x，△AMN的面积为y，则y关于x的函数图象的大致形状是（ ）‎ A． B． C． D．‎ ‎【答案】C ‎ ‎2. （2011山东威海，12，3分）如图，‎ 在正方形ABCD中，AB=‎3cm，动点M自A点出发沿AB方向以每秒‎1cm的速度运动，同时动点N自A点出发沿折线AD—DC—CB以每秒‎3cm的速度运动，到达B点时运动同时停止，设△AMN的面积为y（cm2），运动时间为x（秒），则下列图象中能大致反映y与x之间的函数关系的是（ ）‎ ‎【答案】B ‎3. （2011甘肃兰州，14，4分）如图，正方形ABCD的边长为1，E、F、G、H分别为各 边上的点，且AE=BF=CG=DH，设小正方形EFGH的面积为S，AE为x，则S关于x的函数图象大致是 A B C D E F G H x y ‎-1‎ O ‎1‎ x y ‎1‎ O ‎1‎ x y O ‎1‎ x y ‎1‎ O ‎1‎ ‎1‎ A． B． C． D．‎ ‎【答案】B ‎4. ‎ 二、填空题 ‎1.‎ ‎2. ‎ ‎3. ‎ ‎4. ‎ ‎5. ‎ 三、解答题 ‎1. （2011浙江省舟山，24，12分）已知直线（＜0）分别交轴、轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作轴的垂线交直线AB于点C，设运动时间为秒．‎ ‎（1）当时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．‎ ‎① 直接写出＝1秒时C、Q两点的坐标；‎ ‎② 若以Q、C、A为顶点的三角形与△AOB相似，求的值．‎ ‎（2）当时，设以C为顶点的抛物线与直线AB的另一交点为D（如图2），‎ ‎① 求CD的长；‎ ‎② 设△COD的OC边上的高为，当为何值时，的值最大？ ‎ ‎（第24题图2）‎ ‎（第24题图1）‎ ‎【答案】（1）①C（1，2），Q（2，0）．‎ ‎②由题意得：P(t，0)，C(t，－ｔ＋3)，Q(3－t，0)，‎ 分两种情形讨论：‎ 情形一：当△AQC∽△AOB时，∠AQC=∠AOB＝90°，∴CQ⊥OA，‎ ‎∵CP⊥OA，∴点P与点Q重合，OQ=OP，即3－t=t，∴t=1.5．‎ 情形二：当△ACQ∽△AOB时，∠ACQ=∠AOB＝90°，∵OＡ=OＢ＝3，∴△AOB是等腰直角三角形，∴△ACQ是等腰直角三角形，∵CQ⊥OA，∴AQ=2CP，即t =2（－t ＋3），∴t=2．∴满足条件的t的值是1.5秒或2秒．‎ ‎(2) ①由题意得：C(t，－＋3)，∴以C为顶点的抛物线解析式是，‎ 由，解得x1=t，x2=t；过点D作DE⊥CP于点E，则∠DEC=∠AOB＝90°，DE∥OA，∴∠EDC=∠OAB，∴△DEC∽△AOB，∴，‎ ‎∵AO=4，AB=5，DE=t－（ｔ－）=．∴CD=．‎ ‎②∵CD=，CD边上的高=．∴S△COD=．∴S△COD为定值；‎ 要使OC边上的高h的值最大，只要OC最短．‎ 因为当OC⊥AB时OC最短，此时OC的长为，∠BCO＝90°，∵∠AOB＝90°，∴∠COP＝90°－∠BOC＝∠OBA，又∵CP⊥OA，∴Rt△PCO∽Rt△OAB，‎ ‎∴，OP=，即t=，∴当t为秒时，h的值最大．‎ ‎2. （2011广东东莞，22，9分）如图，抛物线与y轴交于点A，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）.‎ ‎（1）求直线AB的函数关系式；‎ ‎（2）动点P在线段OC上，从原点O出发以每钞一个单位的速度向C移动，过点P作⊥x轴，交直线AB于点M，抛物线于点N，设点P移动的时间为t秒，MN的长为s个单位，求s与t的函数关系式，并写出t的取值范围；‎ ‎（3）设（2）的条件下（不考虑点P与点O，点G重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平等四边形？问对于所求的t的值，平行四边形BCMN是否为菱形？说明理由.‎ ‎【解】（1）把x=0代入，得 把x=3代入，得，‎ ‎ ∴A、B两点的坐标分别（0，1）、（3，）‎ 设直线AB的解析式为，代入A、B的坐标，得 ‎，解得 所以，‎ ‎（2）把x=t分别代入到和 分别得到点M、N的纵坐标为和 ‎∴MN=-（）=‎ 即 ‎∵点P在线段OC上移动，‎ ‎∴0≤t≤3.‎ ‎(3)在四边形BCMN中，∵BC∥MN ‎∴当BC=MN时，四边形BCMN即为平行四边形 由，得 即当时，四边形BCMN为平行四边形 当时，PC=2，PM=，PN=4，由勾股定理求得CM=BN=,‎ 此时BC=CM=MN=BN，平行四边形BCMN为菱形；‎ 当时，PC=1，PM=2，由勾股定理求得CM=,‎ 此时BC≠CM，平行四边形BCMN不是菱形；‎ 所以，当时，平行四边形BCMN为菱形．‎ ‎3. （2011江苏扬州，28,12分）如图，在Rt△ABC中，∠BAC=90º，AB0）‎ ‎（1）△PBM与△QNM相似吗？以图1为例说明理由；‎ ‎（2）若∠ABC=60º，AB=4厘米。‎ ‎① 求动点Q的运动速度；‎ ‎② 设Rt△APQ的面积为S（平方厘米），求S与t的函数关系式；‎ ‎（3）探求BP2、PQ2、CQ2三者之间的数量关系，以图1为例说明理由。‎ ‎ ‎ ‎【答案】解：（1）△PBM与△QNM相似；‎ ‎∵MN⊥BC MQ⊥MP ∴ ∠NMB=∠PMQ=∠BAC =90º ‎∴∠PMB=∠QMN, ∠QNM=∠B =90º－∠C ‎∴ △PBM∽△QNM ‎（2）①∵∠ABC=60º，∠BAC =90º,AB=4,BP=t ‎∴AB=BM=CM=4,MN=4 ‎ ‎∵ △PBM∽△QNM ‎∴ 即：‎ ‎∵P点的运动速度是每秒厘米，‎ ‎∴ Q点运动速度是每秒1厘米。‎ ‎② ∵ AC=12,CN=8‎ ‎∴ AQ=12-8+t=4+t, AP=4－t ‎ ∴ S==‎ ‎（3） BP2+ CQ2 =PQ2‎ ‎ 证明如下： ∵BP=t, ∴BP2=3t2 ‎ ‎∵CQ=8-t ∴CQ2=(8-t)2=64-16t+t2‎ ‎∵PQ2=(4+t)2+3(4-t)2=4t2-16t+64‎ ‎∴BP2+ CQ2 =PQ2‎ ‎4. （2011山东德州23,12分）在直角坐标系xoy中，已知点P是反比例函数图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．‎ ‎（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．‎ ‎（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：‎ ‎①求出点A，B，C的坐标．‎ ‎②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．‎ A P x y K O 图1‎ ‎【答案】解：（1）∵⊙P分别与两坐标轴相切，‎ ‎ ∴ PA⊥OA，PK⊥OK．‎ ‎ ∴∠PAO=∠OKP=90°．‎ ‎ 又∵∠AOK=90°，‎ ‎ ∴ ∠PAO=∠OKP=∠AOK=90°．‎ ‎ ∴四边形OKPA是矩形．‎ ‎ 又∵OA=OK，‎ ‎ ∴四边形OKPA是正方形．……………………2分 O A P x y B C 图2‎ G M ‎（2）①连接PB，设点P的横坐标为x，则其纵坐标为．‎ 过点P作PG⊥BC于G．‎ ‎∵四边形ABCP为菱形，‎ ‎∴BC=PA=PB=PC．‎ ‎∴△PBC为等边三角形．‎ 在Rt△PBG中，∠PBG=60°，PB=PA=x，[来源:学科网]‎ PG=．‎ sin∠PBG=，即．‎ 解之得：x=±2（负值舍去）．‎ ‎∴ PG=，PA=BC=2．……………………4分 易知四边形OGPA是矩形，PA=OG=2，BG=CG=1，‎ ‎∴OB=OG－BG=1，OC=OG+GC=3．‎ ‎∴ A（0，），B（1，0） C（3，0）．……………………6分 设二次函数解析式为：y=ax2+bx+c．‎ 据题意得：‎ 解之得：a=， b=， c=．‎ ‎∴二次函数关系式为：．……………………9分 ‎②解法一：设直线BP的解析式为：y=ux+v，据题意得：‎ ‎ ‎ 解之得：u=， v=．‎ ‎∴直线BP的解析式为：．‎ 过点A作直线AM∥PB，则可得直线AM的解析式为：．‎ 解方程组：‎ 得： ； ．‎ 过点C作直线CM∥PB，则可设直线CM的解析式为：．‎ ‎ ∴0=． ‎ ‎ ∴．‎ ‎∴直线CM的解析式为：．‎ 解方程组：‎ 得： ； ．‎ 综上可知，满足条件的M的坐标有四个，‎ 分别为：（0，），（3，0），（4，），（7，）．…………………12分 解法二：∵，‎ ‎∴A（0，），C（3，0）显然满足条件．‎ 延长AP交抛物线于点M，由抛物线与圆的轴对称性可知，PM=PA．‎ 又∵AM∥BC，‎ ‎∴．‎ ‎∴点M的纵坐标为．‎ 又点M的横坐标为AM=PA+PM=2+2=4．‎ ‎∴点M（4，）符合要求．‎ 点（7，）的求法同解法一．‎ 综上可知，满足条件的M的坐标有四个，‎ 分别为：（0，），（3，0），（4，），（7，）．…………………12分 解法三：延长AP交抛物线于点M，由抛物线与圆的轴对称性可知，PM=PA．‎ 又∵AM∥BC，‎ ‎∴．‎ ‎∴点M的纵坐标为．‎ 即．‎ 解得：（舍），．‎ ‎∴点M的坐标为（4，）．‎ 点（7，）的求法同解法一．‎ 综上可知，满足条件的M的坐标有四个，‎ 分别为：（0，），（3，0），（4，），（7，）．…………………12分 ‎5. （2011山东菏泽，21，9分）如图，抛物线y＝x2＋bx－2与x轴交于A，B两点，与y轴交于C点，且A(－1，0)．‎ ‎（1）求抛物线的解析式及顶点D的坐标；‎ ‎（2）判断△ABC的形状，证明你的结论；‎ ‎（3）点M(m，0)是x轴上的一个动点，当MC＋MD的值最小时，求m的值．‎ A B C D x y O ‎1‎ ‎1‎ 解：（1）把点A(－1，0)的坐标代入抛物线的解析式y＝x2＋bx－2，‎ ‎ 整理后解得，‎ 所以抛物线的解析式为 ．‎ 顶点D． ‎ ‎（2）∵AB=5，AC2=OA2＋OC2=5，BC2=OC2＋OB2=20，‎ ‎ ∴AC2＋BC2=AB2．∴△ABC是直角三角形． ‎ ‎（3）作出点C关于x轴的对称点C′，则C′ (0，2)，OC′=2．‎ 连接C′D交x轴于点M，‎ 根据轴对称性及两点之间线段最短可知，MC＋MD的值最小．‎ 设抛物线的对称轴交轴于点．‎ ‎△C′OM∽△DEM．‎ ‎∴．∴．∴m=．‎ ‎6. （2011山东济宁，23，10分）如图，在平面直角坐标系中，顶点为（，）的抛物线交轴于点，交轴于，两点（点在点的左侧）. 已知点坐标为（，）.‎ ‎（1）求此抛物线的解析式；‎ ‎（2）过点作线段的垂线交抛物线于点， 如果以点为圆心的圆与直线相切，请判断抛物线的对称轴与⊙有怎样的位置关系，并给出证明；‎ ‎（3）已知点是抛物线上的一个动点，且位于，两点之间，问：当点运动到什么位置时，的面积最大？并求出此时点的坐标和的最大面积. ‎ ‎(第23题)‎ ‎【答案】（1）解：设抛物线为.‎ ‎∵抛物线经过点（0，3），∴.∴.‎ ‎∴抛物线为. ……………………………3分 ‎ (2) 答：与⊙相交. …………………………………………………………………4分 证明：当时，，.‎ ‎ ∴为（2，0），为（6，0）.∴.‎ 设⊙与相切于点，连接，则.‎ ‎∵，∴.‎ 又∵，∴.∴∽.‎ ‎∴.∴.∴.…………………………6分 ‎∵抛物线的对称轴为，∴点到的距离为2.‎ ‎∴抛物线的对称轴与⊙相交. ……………………………………………7分 ‎(3) 解：如图，过点作平行于轴的直线交于点.‎ 可求出的解析式为.…………………………………………8分 设点的坐标为（，），则点的坐标为（，）.‎ ‎ ∴.‎ ‎ ∵,‎ ‎ ∴当时，的面积最大为.‎ ‎ 此时，点的坐标为（3，）. …………………………………………10分 ‎(第23题)‎ ‎7. （2011山东威海，25，12分）如图，抛物线交轴于点，点,交轴于点．点C是点A关于点B的对称点，点F是线段BC的中点，直线过点F且与轴平行．直线过点C，交轴于点D．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）点K为线段AB上一动点，过点K作轴的垂线与直线CD交于点H，与抛物线交于点G,求线段HG长度的最大值；‎ ‎（3）在直线上取点M，在抛物线上取点N，使以点A，C，M，N为顶点的四边是平行四边形，求点N的坐标．‎ 图① 备用图 ‎【答案】 解：（1）设抛物线的函数表达式 ‎∵抛物线与轴交于点，将该点坐标代入上式，得．‎ ‎∴所求函数表达式，即．‎ ‎（2）∵点C是点A关于点B的对称点，点，点，‎ ‎∴点C的坐标是．‎ 将点C的坐标是代入，得．‎ ‎∴直线CD的函数表达式为．‎ 设K点的坐标为，则H点的坐标为，G点的坐标为．‎ ‎∵点K为线段AB上一动点，‎ ‎∴．‎ ‎∴．‎ ‎∵，‎ ‎∴当时，线段HG长度有最大值．‎ ‎（3）∵点F是线段BC的中点，点，点 ，‎ ‎∴点F的坐标为．‎ ‎∵直线过点F且与轴平行，‎ ‎∴直线的函数表达式为．‎ ‎∵点M在直线上，点N在抛物线上 ，‎ ‎∴设点M的坐标为，点N的坐标为．‎ ‎∵点，点 ，∴．‎ 分情况讨论：‎ ① 若线段AC是以点A，C，M，N为顶点的四边是平行四边形的边，则须MN∥AC，且MN＝AC＝8．‎ 当点N在点M的左侧时，．‎ ‎∴，解得．‎ ‎∴N点的坐标为．‎ 当点N在点M的右侧时，．‎ ‎∴，解得．‎ ‎∴N点的坐标为．‎ ‎②若线段AC是以点A，C，M，N为顶点的平行四边形的对角线，由“点C与点A关于点B中心对称”知：点M与点N关于点B中心对称．取点F关于点B对称点P，则点P的坐标为．过点P作NP⊥轴，交抛物线于点N．‎ 将代入，得．‎ 过点N，B作直线NB交直线于点M．‎ 在△BPN和△BFM中，‎ ‎∵‎ ‎∴△BPN≌△BFM．‎ ‎∴NB＝MB．‎ ‎∴四边形点ANCM为平行四边形．‎ ‎∴坐标为的点N符合条件．‎ ‎∴当点N的坐标为，，时，以点A，C，M，N为顶点的四边是平行四边形．‎ ‎8. （2011山东烟台，26,14分）如图，在直角坐标系中，梯形ABCD的底边AB在x轴上，底边CD的端点D在y轴上.直线CB的表达式为y=－x+，点A、D的坐标分别为（－4，0），（0，4）.动点P自A点出发，在AB上匀速运行.动点Q自点B出发，在折线 BCD上匀速运行，速度均为每秒1个单位.当其中一个动点到达终点时，它们同时停止运动.设点P运动t（秒）时，△OPQ的面积为s（不能构成△OPQ的动点除外）.‎ ‎（1）求出点B、C的坐标；‎ ‎（2）求s随t变化的函数关系式；‎ ‎（3）当t为何值时s有最大值？并求出最大值.‎ O x y A B C D P Q O x y A B C D ‎（备用图1）‎ ‎90‎ ‎（备用图2）‎ ‎90‎ O x y A B C D ‎【答案】解：（1）把y＝4代入y＝－x＋，得x＝1.‎ ‎ ∴C点的坐标为（1，4）. ‎ ‎ 当y＝0时，－x＋＝0，‎ ‎∴x＝4.∴点B坐标为（4，0）.‎ ‎（2）作CM⊥AB于M，则CM＝4，BM＝3.‎ ‎∴BC＝＝＝5.‎ ‎∴sin∠ABC＝＝.‎ ‎①当0＜t＜4时，作QN⊥OB于N，‎ 则QN＝BQ·sin∠ABC＝t.‎ ‎∴S＝OP·QN＝（4－t）×t ＝－t2＋t（0＜t＜4）.‎ ‎②当4＜t≤5时，（如备用图1），‎ 连接QO，QP，作QN⊥OB于N.‎ 同理可得QN＝t.‎ ‎∴S＝OP·QN＝×（t－4）×t. ＝t2－t（4＜t≤5）.‎ ‎③当5＜t≤6时，（如备用图2），‎ 连接QO，QP.‎ S＝×OP×OD＝（t－4）×4＝2t－8（5＜t≤6）.‎ ‎（3）①在0＜t＜4时，‎ 当t＝＝2时，‎ S最大＝＝.‎ ‎②在4＜t≤5时，对于抛物线S＝t2－t，当t＝－＝2时，‎ S最小＝×22－×2＝－.‎ ‎∴抛物线S＝t2－t的顶点为（2，－）.‎ ‎∴在4＜t≤5时，S随t的增大而增大.‎ ‎∴当t＝5时，S最大＝×52－×5＝2.[来源:Z,xx,k.Com]‎ ‎③在5＜t≤6时，‎ 在S＝2t－8中，∵2＞0，∴S随t的增大而增大.‎ ‎∴当t＝6时，S最大＝2×6－8＝4.‎ ‎∴综合三种情况，当t＝6时，S取得最大值，最大值是4.‎ ‎（说明：（3）中的②也可以省略，但需要说明：在（2）中的②与③的△OPQ，③中的底边OP和高CD都大于②中的底边OP和高.所以③中的△OPQ面积一定大于②中的△OPQ的面积.）‎ ‎9. （2011四川南充市，22，8分）抛物线y=ax2+bx+c与x轴的交点为A（m－4,0）和B(m,0)，与直线y=－x+p相交于点A和点C(‎2m－4,m－6).‎ ‎(1)求抛物线的解析式；‎ ‎（2）若点P在抛物线上，且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12，求点P,Q的坐标；‎ ‎（3）在（2）条件下，若点M是x轴下方抛物线上的动点，当⊿PQM的面积最大时，请求出⊿PQM的最大面积及点M的坐标。‎ ‎【答案】解：（1）∵点A(m-4,0)和C(‎2m-4,m-6)在直线y=-x+p上 ‎∴解得：‎ ‎∴A(-1,0) B(3,0), C(2,-3) ‎ 设抛物线y=ax2+bx+c=a(x-3)(x+1),‎ ‎∵C(2,-3) ∴a=1‎ ‎∴抛物线解析式为：y=x2-2x-3‎ ‎（2）AC=3,AC所在直线的解析式为：y=-x-1，∠BAC=450‎ ‎∵平行四边形ACQP的面积为12.‎ ‎∴平行四边形ACQP中AC边上的高为=2‎ 过点D作DK⊥AC与PQ所在直线相交于点K,DK= 2,∴DN=4‎ ‎∵ACPQ,PQ所在直线在直线ACD的两侧，可能各有一条，‎ ‎∴PQ的解析式或为y=-x+3或y=-x-5‎ ‎∴解得：或 ‎，此方程组无解.‎ 即P1(3,0), P2(-2,5) ‎ ‎∵ACPQ是平行四边形 ，A(-1,0) C(2,-3)‎ ‎∴当P(3,0)时，Q(6，-3)‎ 当P(-2,5)时，Q(1，2) ‎ ‎∴满足条件的P,Q点是P1(3,0), Q1(6，-3)或 P2(-2,5)，Q2(1，2)‎ （1） 设M(t,t2-2t-3),(-1＜t＜3),过点M作y轴的平行线，交PQ所在直线雨点T,则T(t,-t+3)‎ MT=(-t+3)-( t2-2t-3)=- t2+t+6‎ 过点M作MS⊥PQ所在直线于点S，‎ MS=MT= (- t2+t+6)=- (t-)2+‎ ‎∴当t=时，M（，-），⊿PQM中PQ边上高的最大值为 ‎10．（2011 浙江杭州，24， 12)图形既关于点O中心对称，又关于直线AC，BD对称，AC＝10，BD＝6，已知点E，M是线段AB上的动点(不与端点重合)，点O到EF，MN的距离分别为，．△OEF与△OGH组成的图形称为蝶形．[来源:学。科。网Z。X。X。K]‎ ‎(1)求蝶形面积S的最大值；‎ ‎(2)当以EH为直径的圆与以MQ为直径的圆重合时，求与满足的关系式，并求的取值范围．‎ ‎【答案】(1) 如图，设EF与AC交于点K，由△OEF∽△ABD，得，，‎ ‎，，整理得，当时，蝶形面积S的最大，最大值为．‎ ‎(2) 如图，设MN与AC交于点L，由(1)得，则，‎ ‎ ‎ 由OK2+EK2＝OE2，OL2+ML2＝OM2，得OK2+EK2＝OL2+ML2，，整理得，当点E，M不重合时，，．当OE⊥AB时，，所以 ‎2）当点重合时，则，此时的取值范围为.‎ 解法二：（1）由题意，得四边形是菱形.‎ 由，得，，即 所以当时，.‎ ‎（2）根据题意，得.‎ 如图，作于， 关于对称线段为，‎ ‎1）当点不重合时，则在的两侧，易知.‎ ‎，‎ 由，得 ‎，即 ‎，此时的取值范围为且 ‎2）当点重合时，则，此时的取值范围为.‎ ‎11. (2011 浙江湖州，24，14)如图1．已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上,M是BC的中点．P(0，m)是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．‎ ‎(1) 求点D的坐标（用含m的代数式表示）；‎ ‎(2) 当△APD是等腰三角形时，求m的值；‎ ‎(3) 设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2）．当点P从点O向点C运动时，点H也随之运动．请直接写出点H所经过 的路径长．（不必写解答过程）‎ ‎【答案】解：（1）由题意得CM=BM，∵∠PMC＝∠DMB，∴Rt△PMC≌Rt△DMB，∴DB＝PC，∴DB＝2－m，AD＝4－m，∴点D的坐标为（2，4－m）.‎ ‎（2）分三种情况：①若AP＝AD，则，解得.‎ ② 若PD＝PA，过P作PF⊥AB于点F（如图），则AF＝FD,，又OP＝AF，∴，解得，‎ ③ 若DP＝DA，∵△PMC≌△DMB，∴，∵，∴， 解得.‎ 综上所述，当△APD是等腰三角形时，过m的值为.‎ ‎（3）点H经过的路径长为.‎ ‎12. （2011宁波市，26，10分）如图．平面直角坐标系xOy中，点B的坐标为（－2，2），点B的坐标为（6，6），抛物线经过A、O、B三点，线段AB交y轴与点E．‎ ‎（1）求点E的坐标；‎ ‎（2）求抛物线的函数解析式；‎ ‎（3）点F为线段OB上的一个动点（不与O、B重合），直线EF 与抛物线交与M、N两点（点N在y轴右侧），连结ON、BN，当点F在线段OB上运动时，求BON的面积的最大值，并求出此时点N的坐标；‎ ‎（4）连结AN，当BON的面积的最大时，在坐标平面内使得BOP与OAN相似（点B、O、N对应）的点P的坐标．‎ ‎【答案】26．解：（1）设直线AB的函数解析式为y＝mx＋n 将点A（－2，2），B（6，6）代入得：‎ 得m＝，n＝3‎ ‎∴y＝x＋3‎ 当x＝0时y＝3 ∴E(0，3)‎ 设抛物线的函数解析式为y＝ax＋bx 将A（－2，2）B(6，6)代入得解得a＝，b＝－ ‎∴抛物线的解析式为y＝x2－x ‎（3）‎ 过点N做x轴的垂线NG，垂足为G，交OB于点Q，过B作BH⊥x轴于H，设N(x， x2－x)‎ 则Q（x，x）‎ 则SBON ＝ SBON ＋ SBON ‎ ‎＝×QN×OG＋×QN×HG ‎＝×QN×(OG＋HG)＝×QN×OH＝〔x－(x2－x) 〕×6＝－x2＋x＝－(x－3)2＋(0＜x＜6)‎ ‎∴当x＝3时，BON面积最大，最大值为 此时点N的坐标为（3， ）‎ ‎（4）过点A作AS⊥GQ于S ‎∵A(－2，2)，B(6，6)，N（3， ）‎ ‎∴∠AOE＝∠OAS＝∠BOH＝45°，OG＝3，NG＝，NS＝，AS＝5‎ 在RtSAN 和RtNOG中 ‎∴tan∠SAN＝ tan∠NOG＝ ‎∴∠SAN＝∠NOG ‎∴∠OAS－∠ASN＝∠BOG－∠NOG ‎∴∠OASN＝∠BON ‎∴ON的延长线上存在一点P，使BOP～OAN ‎∵A(－2，2)， N（3， ）‎ 在RtASN中 AN＝＝ 当BOP～OAN时 ＝ ∴＝ ∴OP＝ 过点P作PT⊥x轴于点T ‎∴OPT～ONG ∴＝＝ 设P（4t，t）在在RtPOT中，有（4t）2＋t2＝()2‎ ‎∴t1＝ ，t2＝－（舍）‎ ‎∴点P的坐标为（15，）‎ 将OBP沿直线OB返折，可得出另一个满足条件的点(，15)，由以上推理可知，当点P的坐标为（15，）或(，15)时BOP与OAN相似．‎ ‎13. （2011浙江衢州，24,12分）已知两直线分别经过点，点 ‎，并且当两条直线同时相交于轴正半轴的点时，恰好有，经过点的抛物线的对称轴于直线交于点，如图所示.‎ 求点的坐标，并求出抛物线的函数解析式. ‎ 抛物线的对称轴被直线，抛物线，直线和轴依次截得三条线段，问这三条线段有何数量关系？请说明理由.‎ 当直线绕点旋转时，与抛物线的另一个交点为.请找出使为等腰三角形的点.简述理由，并写出点的坐标.‎ ‎（第24题）‎ ‎【答案】（1）解法1：由题意易知 由题意，可设抛物线的函数解析式为.‎ 把的坐标分别代入，得 解这个方程组，得 抛物线的函数解析式为 解法2：由勾股定理，得 又 由题意可设抛物线的函数解析式为把代入函数解析式得 所以抛物线的函数解析式为 ‎（2）解法1：截得三条线段的数量关系为 理由如下：‎ 可求得直线的解析式为，直线的解析式为，抛物线的对称轴为直线.由此可求得点的坐标为，点的坐标为，点的坐标为，点的坐标为.‎ 解法2：截得三条线段的数量关系为 理由如下：‎ 由题意可知则可得 ‎.‎ 由顶点的坐标为得,‎ ‎(3)解法1：（i）以点为圆心，线段长为半径画圆弧，交抛物线于点，由抛物线的对称性可知点为点关于直线的对称点.‎ 所以点的坐标为，此时,为等腰三角形.‎ ‎（ii）当以点为圆心，线段长为半径画圆弧时，与抛物线交点为点和点，而三点在同一直线上，不能构成三角形.‎ ‎（iii）作线段的中垂线，由点是的中点，且，可知经过点， ‎ 此时，有点即点坐标为，使为等腰三角形.‎ 与抛物线的另一交点即为 ‎ 综上所述，当点的坐标为 时，为等腰三角形 解法2：当点的坐标分别为 ‎ 理由如下：‎ ‎（i）链接，交抛物线于点，易知点的坐标为 .‎ 又点的坐标为，则 ‎ ‎ 可求得，且，即为正三角形.‎ 为正三角形 ‎ 当与抛物线交于点，即时，符合题意，此时点的坐标为 ‎（ii）连接，由，易知为等腰三角形 当过抛物线顶点于点时，符合题意，此时点的坐标为.‎ ‎（iii）当点在抛物线对称轴右边时，只有点与点重合时，满足，但此时，三点在同一直线上，不能构成三角形.‎ 综上所述，当点的坐标分别为时，为等腰三角形. ‎ ‎14. (2011浙江绍兴，24，14分)抛物线与轴交于点，顶点为，对称轴与轴交于点.‎ ‎（1）如图1，求点的坐标及线段的长；‎ ‎（2）点在抛物线上，直线交轴于点，连接.‎ ‎①若含45°角的直线三角板如图2所示放置，其中，一个顶点与重合，直角顶点在上，另一顶点在上，求直线的函数解析式；‎ ‎②若含30°角的直角三角板一个顶点与点重合，直角顶点在直线上，另一个顶点在上，求点的坐标. ‎ 第24题图2‎ 第24题图1‎ ‎【答案】解：（1）把代入得，‎ 点，‎ 为对称轴，，‎ ‎.‎ ‎（2）①如图1，过点作轴，交轴于点，‎ 过点作，交于点，‎ 四边形为矩形，‎ 四边形为正方形，‎ 为等腰直角三角形，‎ 设直线的函数解析式为，‎ 直线上两点的坐标为，‎ 代入求得，‎ 直线的函数解析式为.‎ ‎②当点 ‎15. （2011浙江台州，24,14分）已知抛物线与y轴交于点A，它的顶点为B，点A、B关于原点O的对称点分别是点C、D。若点A、B、C、D中任何三点都不在一直线上，则称四边形ABCD为抛物线的伴随四边形，直线AB为抛物线的伴随直线。‎ ‎（1）如图1，求抛物线的伴随直线的解析式；‎ ‎（2）如图2，若（m>0）的伴随直线是y=x－3，伴随四边形的面积为12，求此抛物线的解析式；‎ ‎（3）如图3，若抛物线的伴随直线是y=－2x+b（b>0），且伴随四边形ABCD是矩形。‎ ‎① 用含b的代数式表示m,n的值；‎ ‎② 在抛物线的对称轴上是否存在点P，使得△PBD是一个等腰三角形？若存在，请直接写出点P的坐标（用含b的代数式）；若不存在，请说明理由。‎ ‎【答案】解：(1)设直线AB的解析式为y=kx+b.由题意，得:A(0，5)，B(2，1)‎ ‎ ∴ ∴k=-2 ,b=5‎ ‎ ∴直线AB的解析式为y=-2x+5‎ ‎ (2) 由伴随直线是y=x－3，得：A(0，-3)，C(0，3) ∴ AC=6‎ ‎ 由伴随四边形的面积为12，得：△ABC的面积为6= ‎ ‎ ∴m=±2 ∵m>0 ∴m=2‎ ‎ 当m=2时，y=-1，顶点为（2，-1）， 且过点C（0，3）‎ ‎∴抛物线的解析式为y=。‎ ‎ (3) ① 如图，作BE⊥x轴，‎ 由题意，得：‎ ‎ A（0,b）,C (0,-b)‎ ‎∵抛物线的顶点B（m,n）在y=－2x+b（b>0）上，‎ ‎∴n=‎-2m+b B(m, ‎-2m+b)‎ 在矩形ABCD中，OC=OB ‎ ‎∴OC2=OB2‎ 即：‎ ‎∴m(‎5m-4b)=0‎ ‎∴m1=0(舍去)，m2=‎ ‎∴n=‎-2m+b=‎ ‎∴ ,；‎ ‎ ② 存在，有4个点：(，),( ，),( ，),( ，)‎ ‎16. （2011浙江义乌，24，12分）已知二次函数的图象经过A（2，0）、C(0，12) 两点，且对称轴为直线x=4. 设顶点为 点P，与x轴的另一交点为点B.‎ ‎（1）求二次函数的解析式及顶点P的坐标；‎ ‎（2）如图1，在直线 y=2x上是否存在点D，使四边形OPBD为等腰梯形？若存在，求出点D的坐标；若不存在，请说明理由；‎ ‎（3）如图2，点M是线段OP上的一个动点（O、P两点除外），以每秒个单位长度的速度由点P向点O 运动，过点M作直线MN∥x轴，交PB于点N. 将△PMN沿直线MN对折，得到△P1MN. 在动点M的运动过程中，设△P1MN与梯形OMNB的重叠部分的面积为S，运动时间为t秒. 求S关于t的函数关系式. ‎ O P C B A x y 图1‎ 图2‎ M O A x P N C B y ‎【答案】（1）设二次函数的解析式为y=ax2+bx+c ‎ 由题意得 解得 ‎ ∴二次函数的解析式为y= x2－8x+12‎ ‎ 点P的坐标为（4，－4） ‎ ‎（2）存在点D，使四边形OPBD为等腰梯形. 理由如下：‎ DO x A O B C P y 当y=0时，x2-8x+12=0 ∴x1=2 ， x2=6‎ ‎∴点B的坐标为（6，0）‎ 设直线BP的解析式为y=kx+m ‎ 则 解得 ‎ ∴直线BP的解析式为y=2x－12‎ ‎ ∴直线OD∥BP ‎ ∵顶点坐标P（4， －4） ∴ OP=4‎ ‎ 设D(x，2x) 则BD2=（2x）2+(6－x)2‎ ‎ 当BD=OP时，（2x）2+(6－x)2=32‎ ‎ 解得：x1=，x 2=2‎ ‎ 当x2=2时，OD=BP=，四边形OPBD为平行四边形，舍去 ‎ ∴当x=时四边形OPBD为等腰梯形 ‎ ∴当D(，)时，四边形OPBD为等腰梯形 ‎（3）① 当0＜t≤2时，‎ x P1‎ M A O B C P N y H ‎∵运动速度为每秒个单位长度，运动时间为t秒，‎ 则MP=t ∴PH=t，MH=t，HN=t ∴MN=t ‎∴S=t·t·=t2 ‎ ‎ ② 当2＜t＜4时，P‎1G=2t－4，P1H=t ‎ ‎x P1‎ M A O B C P N G H E F y ‎∵MN∥OB ∴ ∽‎ ‎∴ ∴ ‎ ‎ ∴ =3t2－12t+12‎ ‎∴S=t2－(3t2－12t+12)= －t2+12t－12‎ ‎∴ 当0＜t≤2时，S=t2‎ ‎ 当2＜t＜4时，S=－t2+12t－12 。‎ ‎17. （2011四川重庆，26，12分）如图，矩形ABCD中，AB＝6，BC＝2，点O是AB的中点，点P在AB的延长线上，且BP＝3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速动动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速动动，点E、F同时出发，当两点相遇时停止运动．在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧，设动动的时间为t秒(t≥0)．‎ ‎(1)当等边△EFG的边FG恰好经过点C时，求运动时间t的值；‎ ‎(2)在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；‎ ‎(3)设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存在，求出对应的t的值；若不存在，请说明理由．[来源:Zxxk.Com]‎ ‎【答案】(1)当等边△EFG的边FG恰好经过点C时(如图)，∠CFB＝60°，BF＝3－t，在Rt△CBF中，BC＝2，∴tan∠CFB＝，∴tan 60°=，∴BF＝2，∴t＝3－t ＝2，∴t＝1．‎ ‎ (2)当0≤t＜1时，S= 2 t＋4；当1≤t＜3时，S= t 2+3 t＋；当3≤t＜4时，S= －4 t＋20；当4≤t＜6时，S= t2－12 t＋36．‎ ‎(3)存在，理由如下：‎ ‎ 在Rt△ABC中，tan∠CAB＝=，∴∠CAB=30°．‎ 又∵∠HEO=60°，∴∠HAE=∠AHE=30°．‎ ‎∴AE=HE=3－t或t－3．‎ ‎（ⅰ）当AH=AO=3时（如图②），过点E作EM⊥AH于M，则AM=AH=．‎ 在Rt△AME中，cos∠MAE＝，即cos 30°=，∴AE=，‎ 即3－t=或t－3=，t=3－或3＋． ‎ ‎（ⅱ）当HA=HO时（如图③），则∠HOA=∠HAO=30°，‎ 又∵∠HEO=60°，∴∠EHO=90°．‎ ‎∴EO=2HE=2AE．又∵AE＋EO=3，∴AE＋2AE=3．‎ ‎∴AE=1．即3－t=1或t－3=1，t=2或4． ‎ ‎（ⅲ）当OH=OA时（如图④），则∠OHA=∠OAH=30°，‎ ‎∴∠HOB=60°=∠HEB．∴点E和O重合，∴AE=3．‎ 即3－t=3或t－3=3，t=6（舍去）或t=0．‎ ‎ ‎ 综上所述，存在5个这样的值，使△AOH是等腰三角形，即： t=3－或t=3＋或t=2或t=4或t=0． ‎ ‎18. （2011浙江省嘉兴，24，14分）已知直线（＜0）分别交轴、轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作轴的垂线交直线AB于点C，设运动时间为秒．‎ ‎（1）当时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．‎ ‎① 直接写出＝1秒时C、Q两点的坐标；‎ ‎② 若以Q、C、A为顶点的三角形与△AOB相似，求的值．‎ ‎（2）当时，设以C为顶点的抛物线与直线AB的另一交点为D（如图2），‎ ‎① 求CD的长；‎ ‎② 设△COD的OC边上的高为，当为何值时，的值最大？ ‎ ‎（第24题图2）‎ ‎（第24题图1）‎ ‎【答案】（1）①C（1，2），Q（2，0）．‎ ‎②由题意得：P(t，0)，C(t，－ｔ＋3)，Q(3－t，0)，‎ 分两种情形讨论：‎ 情形一：当△AQC∽△AOB时，∠AQC=∠AOB＝90°，∴CQ⊥OA，‎ ‎∵CP⊥OA，∴点P与点Q重合，OQ=OP，即3－t=t，∴t=1.5．‎ 情形二：当△ACQ∽△AOB时，∠ACQ=∠AOB＝90°，∵OＡ=OＢ＝3，∴△AOB是等腰直角三角形，∴△ACQ是等腰直角三角形，∵CQ⊥OA，∴AQ=2CP，即t =2（－t ＋3），∴t=2．∴满足条件的t的值是1.5秒或2秒．‎ ‎(2) ①由题意得：C(t，－＋3)，∴以C为顶点的抛物线解析式是，‎ 由，解得x1=t，x2=t；过点D作DE⊥CP于点E，则∠DEC=∠AOB＝90°，DE∥OA，∴∠EDC=∠OAB，∴△DEC∽△AOB，∴，‎ ‎∵AO=4，AB=5，DE=t－（ｔ－）=．∴CD=．‎ ‎②∵CD=，CD边上的高=．∴S△COD=．∴S△COD为定值；‎ 要使OC边上的高h的值最大，只要OC最短．‎ 因为当OC⊥AB时OC最短，此时OC的长为，∠BCO＝90°，∵∠AOB＝90°，∴∠COP＝90°－∠BOC＝∠OBA，又∵CP⊥OA，∴Rt△PCO∽Rt△OAB，‎ ‎∴，OP=，即t=，∴当t为秒时，h的值最大．‎ ‎19. （2011福建泉州，25，12分）在直角坐标系xoy中，已知点P是反比例函数 图象上一个动点，以P为圆心的圆始终与y轴相切，设切点为A．‎ ‎（1）如图1，⊙P运动到与x轴相切，设切点为K，试判断四边形OKPA的形状，并说明理由．‎ ‎（2）如图2，⊙P运动到与x轴相交，设交点为B，C．当四边形ABCP是菱形时：‎ ‎①求出点A，B，C的坐标．‎ A P x y K O 第25题 图1‎ ‎②在过A，B，C三点的抛物线上是否存在点M，使△MBP的面积是菱形ABCP面积的．若存在，试求出所有满足条件的M点的坐标，若不存在，试说明理由．‎ ‎[来源:学*科*网]‎ ‎【答案】解：（1）∵⊙P分别与两坐标轴相切，‎ ‎ ∴ PA⊥OA，PK⊥OK．‎ ‎ ∴∠PAO=∠OKP=90°．‎ ‎ 又∵∠AOK=90°，‎ ‎ ∴ ∠PAO=∠OKP=∠AOK=90°．‎ ‎ ∴四边形OKPA是矩形．‎ ‎ 又∵OA=OK，‎ ‎ ∴四边形OKPA是正方形．……………………2分 ‎（2）①连接PB，设点P的横坐标为x，则其纵坐标为．‎ O A P x y B C 图2‎ G M 过点P作PG⊥BC于G．‎ ‎∵四边形ABCP为菱形，‎ ‎∴BC=PA=PB=PC．‎ ‎∴△PBC为等边三角形．‎ 在Rt△PBG中，∠PBG=60°，PB=PA=x，‎ PG=．‎ sin∠PBG=，即．‎ 解之得：x=±2（负值舍去）．‎ ‎∴ PG=，PA=BC=2．……………………4分 易知四边形OGPA是矩形，PA=OG=2，BG=CG=1，‎ ‎∴OB=OG－BG=1，OC=OG+GC=3．‎ ‎∴ A（0，），B（1，0） C（3，0）．……………………6分 设二次函数解析式为：y=ax2+bx+c．‎ 据题意得：‎ 解之得：a=， b=， c=．‎ ‎∴二次函数关系式为：．……………………9分 ‎②解法一：设直线BP的解析式为：y=ux+v，据题意得：‎ ‎ ‎ 解之得：u=， v=．‎ ‎∴直线BP的解析式为：．‎ 过点A作直线AM∥PB，则可得直线AM的解析式为：．‎ 解方程组：‎ 得： ； ．‎ 过点C作直线CM∥PB，则可设直线CM的解析式为：．‎ ‎ ∴0=． ‎ ‎ ∴．‎ ‎∴直线CM的解析式为：．‎ 解方程组：‎ 得： ； ．‎ 综上可知，满足条件的M的坐标有四个，‎ 分别为：（0，），（3，0），（4，），（7，）．…………………12分 解法二：∵，‎ ‎∴A（0，），C（3，0）显然满足条件．‎ 延长AP交抛物线于点M，由抛物线与圆的轴对称性可知，PM=PA．‎ 又∵AM∥BC，‎ ‎∴．‎ ‎∴点M的纵坐标为．‎ 又点M的横坐标为AM=PA+PM=2+2=4．‎ ‎∴点M（4，）符合要求．‎ 点（7，）的求法同解法一．‎ 综上可知，满足条件的M的坐标有四个，‎ 分别为：（0，），（3，0），（4，），（7，）．…………………12分 解法三：延长AP交抛物线于点M，由抛物线与圆的轴对称性可知，PM=PA．‎ 又∵AM∥BC，‎ ‎∴．‎ ‎∴点M的纵坐标为．‎ 即．‎ 解得：（舍），．‎ ‎∴点M的坐标为（4，）．‎ 点（7，）的求法同解法一．‎ 综上可知，满足条件的M的坐标有四个，‎ 分别为：（0，），（3，0），（4，），（7，）．…………………12分 ‎20．（2011福建泉州，26，14分）如图，在平面直角坐标系xOy中，直线AB与x轴交于点A， 与y轴交于点B， 且OA = 3，AB = 5．点P从点O出发沿OA以每秒1个单位长的速度向点A匀速运动，到达点A后立刻以原来的速度沿AO返回；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交折线QB－BO－OP于点E．点P、Q同时出发，当点Q到达点B时停止运动，点P也随之停止．设点P、Q运动的时间是t秒（t＞0）．‎ ‎（1）求直线AB的解析式；‎ ‎（2）在点P从O向A运动的过程中，求△APQ的面积S与t之间的函数关系式（不必写出t的取值范围）； ‎ ‎（3）在点E从B向O运动的过程中，完成下面问题：‎‎（第26题）‎ ‎①四边形QBED能否成为直角梯形？若能，请求出t的值；‎ 若不能，请说明理由；‎ ‎②当DE经过点O时，请你直接写出t的值．‎ ‎【答案】解：解：（1）在Rt△AOB中，OA = 3，AB = 5，由勾股定理得.‎ ‎∴A（3，0），B（0，4）．‎ 设直线AB的解析式为.‎ ‎∴ 解得 ‎ ‎∴直线AB的解析式为．…………2分 ‎（2）如图，过点Q作QF⊥AO于点F.‎ ‎∵ AQ = OP= t，∴．‎ 由△AQF∽△ABO，得． ‎ ‎∴．∴． …………2分 ‎∴，‎ ‎∴．………………………4分 ‎（3）四边形QBED能成为直角梯形．‎ ‎ ①如图，当DE∥QB时，‎ ‎ ∵DE⊥PQ，‎ ‎∴PQ⊥QB，四边形QBED是直角梯形．‎ ‎ 此时∠AQP=90°．‎ 由△APQ ∽△ABO，得.‎ ‎∴． ‎ 解得． ……………………………6分 ‎②如图，当PQ∥BO时，‎ ‎∵DE⊥PQ，‎ ‎∴DE⊥BO，四边形QBED是直角梯形．‎ 此时∠APQ =90°．‎ 由△AQP ∽△ABO，得 ‎ 即．‎ 解得． ………………………10分 ‎ ‎（4）或． ………………………14分 ‎21. （2011湖南常德，26，10分）如图11，已知抛物线过点A（0，6），B（2，0），C（7，）.‎ ‎ （1）求抛物线的解析式；‎ ‎（2）若D是抛物线的顶点，E是抛物线的对称轴与直线AC的交点，F与E关于D对称，求证：∠CFE=∠AFE；‎ O ‎ A ‎ B ‎ E ‎ 图 11‎ D ‎ F ‎ C ‎ ‎ y x ‎ N M ‎（3）在y轴上是否存在这样的点P，使△AFP与△FDC相似，若有，请求出所有合条件的点P的坐标；若没有，请说明理由.‎ 解：（1）抛物线经过点A（0，6），B（2，0），C（7，）的抛物线的解析式为y=ax2+bx+c，‎ 则：‎ 解得 ‎∴ 此抛物线的解析式为 ‎ ‎（2）过点A作AM∥x轴，交FC于点M，交对称轴于点N.‎ ‎∵抛物线的解析式可变形为 ‎∴抛物线对称轴是直线x =4，顶点D的坐标为（4，－2）.则AN=4.‎ 设直线AC的解析式为,‎ 则有，解得.‎ ‎∴ 直线AC的解析式为 当x=4时，‎ ‎∴点E的坐标为（4，4），‎ ‎∵点F与E关于点D对称，则点F的坐标为（4，－8）‎ 设直线FC的解析式为,‎ 则有，解得.‎ ‎∴ 直线AC的解析式为 ‎∵AM与x轴平行，则点M的纵坐标为6.‎ 当y=6时，则有解得x=8.‎ ‎∴AM=8,MN=AM—MN=4‎ ‎∴AN=MN ‎∵FN⊥AM ‎∴∠ANF=∠MNF 又NF=NF ‎∴△ANF≌△MNF ‎∴∠CFE=∠AFE ‎（3）∵C的坐标为（7，），F坐标为（4，－8）‎ ‎∴‎ ‎∵又A的坐标为（0，6），则，‎ 又DF=6，‎ 若△AFP∽△DEF ‎∵EF∥AO，则有∠PAF=∠AFE，‎ 又由（2）可知∠DFC=∠AFE ‎∴∠PAF=∠DFC 若△AFP1∽△FCD 则,即,解得P1A=8.‎ ‎∴O P1=8－6=2‎ ‎∴P1的坐标为（0，－2）.‎ 若△AFP2∽△FDC 则,即,解得P2A=.‎ ‎∴O P2=－6=.‎ ‎∴P2的坐标为（0，－）.‎ 所以符合条件的点P的坐标不两个，分别是P1（0，－2），P2（0，－）.‎ ‎22. （2011湖南邵阳，24，12分）如图（十一）所示，在平面直角坐标系Oxy中，已知点A（，0），点C（0,3）点B是x轴上一点（位于点A右侧），以AB为直径的圆恰好经过点C。‎ ‎（1）求角ACB的度数；‎ ‎（2）已知抛物线y=ax2+bx+3经过A，B两点，求抛物线的解析式；‎ ‎（3）线段BC上是否存在点D，使△BOD为等腰三角形？若存在，则求出所有符合条件的点D的坐标；若不存在，请说明理由。‎ ‎【答案】解：（1）90°；‎ ‎（2）Rt△ABC中，∵OA×OB=OC 2，‎ ‎∴OB=4.‎ 抛物线为y=a（x-4）（x+）= ax2+bx+3，‎ 比较常数项得a=，抛物线的方程为y=（x-4）（x+）。‎ （1） 存在。‎ 直线BC的方程为3x+4y=12，设点D（x，y）。‎ ‎①若BD=OD，则点D在OB的中垂线上，点D横坐标为2，纵坐标为，即D1（2，）为所求。‎ ‎②若OB=BD=4，则，，‎ 得y=，x=，点D2（，）为所求。‎ ‎23. （2011江苏苏州，29,10分）已知二次函数y=a（x2-6x+8）（a>0）的图象与x轴分别交于点A、B，与y轴交于点C.点D是抛物线的顶点.‎ ‎（1）如图①，连接AC，将△OAC沿直线AC翻折，若点O的对应点O′恰好落在该抛物线的对称轴上，求实数a的值；‎ ‎（2）如图②，在正方形EFGH中，点E、F的坐标分别是（4,4）、（4,3），边HG位于边EF的右侧.小林同学经过探索后发现一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等（即这四条线段不能构成平行四边形）.”若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；‎ ‎（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标t是大于3‎ 的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等（即这四条线段能够成平行四边形）？请说明理由.‎ ‎【答案】解：（1）令y=0，由a（x2-6x+8）=0解得x1=2，x2=4；‎ 令x=0，解得y=8a.‎ ‎∴点A、B、C的坐标分别是（2,0）、（4,0）、（0,8a），‎ 该抛物线对称轴为直线x=3.‎ ‎∴OA=2，‎ 如图①，设抛物线对称轴与x轴的交点为M，则AM=1.‎ 由题意得O′A=OA=2.‎ ‎∴O′A=2AM，∴∠O′AM=60°.‎ ‎∴∠OAC=∠ O′AC=60°.‎ ‎∴OC=·AO=2，即8a=2，∴a=.‎ ‎（2）若点P是边EF或边FG上的任意一点，结果同样成立.‎ ‎（I）如图②，设P是边EF上的任意一点（不与点E重合），连接PM.‎ ‎∵点E（4,4）、F（4,3）与点B（4,0）在一直线上，点C在y轴上，‎ ‎∴PB＜4，PC≥4，∴PC＞PB.‎ 又PD＞PM＞PB，PA＞PM＞PB，‎ ‎∴PB≠PA，PB≠PC，PB≠PD，‎ ‎∴此时线段PA、PB、PC、PD不能构成平行四边形.‎ ‎（II）设P是边FG上的任意一点（不与点G重合），‎ 点F的坐标是（4,3）点G的坐标是（5,3）.‎ ‎∴FB=3，GB=，∴3≤PB＜，‎ ‎∵PC≥4，∴PC＞PB.‎ 又PD＞PM＞PB，PA＞PM＞PB，‎ ‎∴PB≠PA，PB≠PC，PB≠PD，‎ ‎∴此时线段PA、PB、PC、PD不能构成平行四边形.‎ ‎（3）存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等（即这四条线段能够成平行四边形）.‎ 如图③，∵点A、B是抛物线与x轴交点，点P在抛物线对称轴上，‎ ‎∴PA=PB.‎ ‎∴当PC=PD时，线段PA、PB、PC、PD能构成平行四边形.‎ ‎∵点C的坐标是（0,8a），点D的坐标为（3，-a），点P的坐标是（3，t），‎ ‎∴PC2=32+（t-8a）2，PD2=（t+a）2，‎ 由PC=PD得PC2=PD2，∴32+（t-8a）2=（t+a）2，‎ 整理得7a2-2ta+1=0，∴△=4t2-28.‎ ‎∵t是大于3的常数，∴△=4t2-28＞0，‎ ‎∴方程7a2-2ta+1=0有两个不相等的实数根a==，‎ 显然，a=＞0，满足题意.‎ ‎∴当t是一个大于3的常数时，存在一个正数a=，使得线段PA、PB、PC、PD 能构成平行四边形.‎ ‎24. （2011江苏宿迁,27,12分）如图，在边长为2的正方形ABCD中，P为AB的中点，Q为边CD上一动点，设DQ＝t（0≤t≤2），线段PQ的垂直平分线分别交边AD、BC于点M、N，过Q作QE⊥AB于点E，过M作MF⊥BC于点F．‎ ‎ （1）当t≠1时，求证：△PEQ≌△NFM；‎ ‎ （2）顺次连接P、M、Q、N，设四边形PMQN的面积为S，求出S与自变量t之间的函数关系式，并求S的最小值．‎ ‎（第27题）‎ ‎【答案】‎ 解：（1）∵四边形ABCD是正方形 ‎∴∠A＝∠B＝∠D＝90°，AD＝AB ‎∵QE⊥AB，MF⊥BC ‎∴∠AEQ＝∠MFB＝90°[来源:学。科。网]‎ ‎ ∴四边形ABFM、AEQD都是矩形 ‎ ∴MF＝AB，QE＝AD，MF⊥QE ‎ 又∵PQ⊥MN ‎∴∠EQP＝∠FMN 又∵∠QEP＝∠MFN＝90°‎ ‎∴△PEQ≌△NFM．‎ ‎ （2）∵点P是边AB的中点，AB＝2，DQ＝AE＝t ‎∴PA＝1，PE＝1－t，QE＝2‎ 由勾股定理，得PQ＝＝‎ ‎∵△PEQ≌△NFM ‎∴MN＝PQ＝‎ 又∵PQ⊥MN ‎∴S＝＝＝t2－t＋‎ ‎∵0≤t≤2‎ ‎∴当t＝1时，S最小值＝2．‎ 综上：S＝t2－t＋，S的最小值为2．‎ ‎25. （2011山东济宁，23，10分）如图，第一象限内半径为2的⊙C与y轴相切于点A，作直径AD，过点D作⊙C的切线l交x轴于点B，P为直线l上一动点，已知直线PA的解析式为：．‎ ‎(1)设点P的纵坐标为p，写出p随k变化的函数关系式；‎ ‎（2）设⊙C与PA交于点M，与AB交于点N，则不论动点P处于直线l上（除点B以外）的什么位置时，都有△AMN∽△ABP，请你对于点P处于图中位置时的两个三角形相似给予证明；‎ ‎（3）是否存在使△AMN的面积等于的k倍？若存在，请求出符合条件的k值；若不存在，请说明理由．‎ A B C D M P l N O 第23题 ‎[来源:学科网]‎ ‎【答案】解：（1）∵y轴和直线l都是⊙C的切线，‎ ‎∴OA⊥AD，BD⊥AD，又OA⊥OB，‎ ‎∴∠AOB=∠OAD=∠ADB= 90°，‎ ‎ ∴四边形OADB是矩形，‎ ‎ ∵⊙C的半径为2，∴AD=OB，‎ ‎ ∵点P在直线l上，∴点P的坐标为（4，p）‎ ‎ 又∵点P也在直线AP上，∴p=4k＋3．‎ ‎　　　(2)连接DN，∵AD是⊙C的直径，∴∠AND= 90°，‎ ‎ ∵∠ADN= 90°—∠DAN，∠ABD= 90°—∠DAN，‎ ‎ ∴∠ADN=∠ABD，‎ ‎∵∠ADN=∠AMN，∴∠AMN=∠ABD，‎ 又∵∠MAN=∠BAP，‎ ‎ ∴△AMN∽△ABP．‎ ‎(3)存在．‎ 理由：把x=0代入y=kx＋3得y=3，即OA=BD=3，‎ 在Rt△ABD中，由勾股定理得，‎ ‎∵S△ABD=，‎ ‎∴，‎ ‎∴，‎ ‎∵△AMN∽△ABP．‎ ‎∴，‎ 即，‎ 当点P在B点上方时，‎ ‎∵，或 ‎，‎ ‎∴．‎ 整理得，解得，，‎ 当点P在B点下方时，‎ ‎∵，‎ ‎，‎ ‎∴，‎ 化简，得，解得，‎ 综合以上所述得，当或时，△AMN的面积等于．‎ ‎26. （2011广东汕头，22，9分）如图，抛物线与y轴交于点A，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）.‎ ‎（1）求直线AB的函数关系式；‎ ‎（2）动点P在线段OC上，从原点O出发以每钞一个单位的速度向C移动，过点P作⊥x轴，交直线AB于点M，抛物线于点N，设点P移动的时间为t秒，MN的长为s个单位，求s与t的函数关系式，并写出t的取值范围；‎ ‎（3）设（2）的条件下（不考虑点P与点O，点G重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平等四边形？问对于所求的t的值，平行四边形BCMN是否为菱形？说明理由.‎ ‎[来源:学科网ZXXK]‎ ‎【解】（1）把x=0代入，得 把x=3代入，得，‎ ‎ ∴A、B两点的坐标分别（0，1）、（3，）‎ 设直线AB的解析式为，代入A、B的坐标，得 ‎，解得 所以，‎ ‎（2）把x=t分别代入到和 分别得到点M、N的纵坐标为和 ‎∴MN=-（）=‎ 即 ‎∵点P在线段OC上移动，‎ ‎∴0≤t≤3.‎ ‎(3)在四边形BCMN中，∵BC∥MN ‎∴当BC=MN时，四边形BCMN即为平行四边形 由，得 即当时，四边形BCMN为平行四边形 当时，PC=2，PM=，PN=4，由勾股定理求得CM=BN=,‎ 此时BC=CM=MN=BN，平行四边形BCMN为菱形；‎ 当时，PC=1，PM=2，由勾股定理求得CM=,‎ 此时BC≠CM，平行四边形BCMN不是菱形；‎ 所以，当时，平行四边形BCMN为菱形．‎ ‎27. （2011四川成都，28,12分）如图，在平面直角坐标系中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知，，△ABC的面积，抛物线 经过A、B、C三点．‎ ‎ (1)求此抛物线的函数表达式；‎ ‎ (2)设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；‎ ‎ (3)在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为？若存在，求出点M的坐标；若不存在，请说明理由．‎ ‎【答案】‎ 解：（1）设，则，‎ S△ABC=（）×===15，‎ ‎∴（负值不合题意，已经舍去），根据抛物线与坐标轴交点的位置，可知A、B、C三点的坐标分别是（-1，0）、（5，0）、（0，-5），代入抛物线，列方程组为：‎ ‎，解得：，，，∴抛物线的解析式为：．‎ ‎（2）如图所示：E是y轴右侧抛物线上异于点B的一个动点，设该点的横坐标是，抛物线的对称轴为，根据轴对称图形的性质可知，对应点F的横坐标是，EF=，若E在轴上面，则对应的函数值是正数，若E在轴下面，则对应的函数值是负数，若矩形EFGH为正方形时，则EF=GH=FG=EH，∴，当 时，解得：（其中不合题意，已经舍去），则EF==，正方形的边长为；当，解得：（其中不合题意，已经舍去），则EF==，正方形的边长为.[来源:学_科_网]‎ ‎（3）如图所示，根据已经容易求出BC=，若要使△MBC中BC边上的高为，必须使S△MBC==35.‎ 设点M的横坐标为，那么根据抛物线的解析式，可知M的坐标为，若点M在轴的上面，则，过M作MN⊥轴，垂足为N，那么S△MBC =S梯形MNOB+S△OBC-S△MNC ，∴，‎ 化简得：，解得或，所以若M在轴上面，满足题意的有两点，分别为（-2，7）、（7，16）；‎ 若M在轴下面，则，过M作MN⊥轴，那么垂足为N，那么S△MBC =S梯形MNOB-S△OBC-S△MNC ，∴，‎ 化简得：，△=，∴所以方程在实数范围无根，所以在轴下面没有满足题意的M点.‎ ‎28. （2011四川内江，加试7，12分）如图，抛物线与x轴交于A、B两点，与y轴交于点C（0，－1），且对釉轴x=1．‎ ‎ (1)求出抛物线的解析式及A、B两点的坐标；‎ ‎ (2)在x轴下方的抛物线上是否存在点D，使四边形ABDC的面积为3．若存在，求出点D的坐标；若不存在，说明理由(使用图1)；‎ ‎ (3)点Q在y轴上，点P在抛物线上，要使Q、P、A、B为顶点的四边形是平行四边形，请求出所有满足条件的点P的坐标(使用图2)．‎ x=1‎ A B O C x y x=1‎ A B O C x y 图1 图2‎ ‎【答案】（1）由得，又 所以抛物线的解析式为 由得x=－1或x=3‎ 所以A（－1，0），B（3，0）‎ ‎（2）假设存在符合条件的点D，设D（x，）‎ 作DE⊥x轴于点E，则OE=x，DE=，BE=3－x，得 化简得， 解得x=1或x=2‎ 故存在符合条件的点D，为D（1，）或D（2，－1）‎ x=1‎ A B O C x y x=1‎ A B O C x y D E P P Q ‎（3）当PQ平行等于AB时，PQ=4，当P在y轴右侧时，P的横坐标为4，当P在y轴左侧时，P的横坐标为－4‎ ‎ 当PQ与AB互相平分时，PQ过AB的中点（1，0），可得P的横坐标为2‎ ‎ 故P的坐标为（4，）或（－4，7）或（2，－1）‎ ‎29.（2011安徽芜湖，24，14分）平面直角坐标系中，如图放置，点A、C的坐标分别为、，将此平行四边形绕点O顺时针旋转，得到.‎ ‎（1）若抛物线过点,求此抛物线的解析式;‎ ‎（2）求和重叠部分的周长;‎ ‎（3）点M是第一象限内抛物线上的一动点，问：点M在何处时△的面积最大？最大面积是多少？并求出此时点的坐标. ‎ ‎【答案】‎ 解: （1）∵由旋转得到，且点A的坐标为，‎ ‎∴点的坐标为. ……………………………………1分 所以抛物线过点.设抛物线的解析式为 ‎，可得 解得 ……………………4分 ‎∴ 过点的抛物线的解析式为. ……………………5分 ‎（2）因为，所以.‎ 所以.又,‎ ‎, ∴△∽△. 又.………………7分 ‎∴. 又△的周长为，‎ 所以△的周长为.………………9分 ‎（3）［解法1］连接，设M点的坐标为，‎ 因为点M在抛物线上，所以，………10分 所以 ‎ ……………12分 因为，所以当时，. △的面积有最大值…………13分 所以当点M的坐标为时，△的面积有最大值，且最大值为…14分 ‎[解法2]设直线的解析式为，∵点的坐标分别为，∴ 解得 ∴.…10分 将直线向右平移，当直线与抛物线只有一个交点M时与y轴交于点P，此时最大，设平移后的直线的解析式为：，则有： 得，‎ 令，得. ‎ ‎∴.解得 ∴点坐标为,点P的坐标为.…12分 因为MP∥,所以△与△同底等高，它们面积相等.‎ 故.‎ 所以当点M的坐标为时，△的面积有最大值，且最大值为 ……14分 ‎30.（2011山东潍坊，24，12分）如图，y关于x的二次函数图象的顶点为M，图象交x轴于A、B两点，交y轴正半轴于D点.以AB为直径做圆，圆心为C，定点E的坐标为（－3,0），连接ED.（m＞0）‎ ‎（1）写出A、B、D三点的坐标；‎ ‎（2）当m为何值时M点在直线ED上？判定此时直线ED与圆的位置关系；‎ ‎（3）当m变化时，用m表示△AED的面积S，并在给出的直角坐标系中画出S关于m的函数图象的示意图.‎ ‎ ‎ ‎【解】（1），，.‎ ‎（2）设直线ED的解析式为，将、代入，得 解得 ‎∴直线ED的解析式为.[来源:学#科#网]‎ ‎∵，‎ ‎∴顶点M的坐标为.‎ 把代入，得.‎ ‎∵，∴.‎ ‎∴当时，点M在直线DE上.‎ 连接CD，C为AB中点，C点坐标为.‎ ‎∵，∴CD=2，点D在圆上.‎ 又∵OE=3，，，.‎ ‎∴.‎ ‎∴∠EDC=90°，‎ ‎∴直线ED与⊙C相切.‎ ‎（3）当时，，即.‎ 当时，，即.‎ 图象示意图如图中的实线部分.‎ ‎12. （2011广东中山，22,9分）如图，抛物线与y轴交于点A，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C（3，0）.‎ ‎（1）求直线AB的函数关系式；‎ ‎（2）动点P在线段OC上，从原点O出发以每钞一个单位的速度向C移动，过点P作⊥x轴，交直线AB于点M，抛物线于点N，设点P移动的时间为t秒，MN的长为s个单位，求s与t的函数关系式，并写出t的取值范围；‎ ‎（3）设（2）的条件下（不考虑点P与点O，点G重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平等四边形？问对于所求的t的值，平行四边形BCMN是否为菱形？说明理由.‎ ‎【解】（1）把x=0代入，得 把x=3代入，得，‎ ‎ ∴A、B两点的坐标分别（0，1）、（3，）‎ 设直线AB的解析式为，代入A、B的坐标，得 ‎，解得 所以，‎ ‎（2）把x=t分别代入到和 分别得到点M、N的纵坐标为和 ‎∴MN=-（）=‎ 即 ‎∵点P在线段OC上移动，‎ ‎∴0≤t≤3.‎ ‎(3)在四边形BCMN中，∵BC∥MN ‎∴当BC=MN时，四边形BCMN即为平行四边形 由，得 即当时，四边形BCMN为平行四边形 当时，PC=2，PM=，由勾股定理求得CM=,‎ 此时BC=CM，平行四边形BCMN为菱形；‎ 当时，PC=1，PM=2，由勾股定理求得CM=,‎ 此时BC≠CM，平行四边形BCMN不是菱形；‎ 所以，当时，平行四边形BCMN为菱形．‎ ‎3. （2011四川成都，20,10分） 如图，已知线段AB∥CD，AD与BC相交于点K，E是线段AD上一动点.‎ ‎ (1)若BK=KC，求的值；‎ ‎ (2)连接BE，若BE平分∠ABC，则当AE=AD时，猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明．再探究：当AE=AD ()，而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论，不必证明．‎ ‎【答案】解：（1）∵AB∥CD，BK=KC，∴==.‎ ‎（2）如图所示，分别过C、D作BE∥CF∥DG分别交于AB的延长线于F、G三点，‎ ‎∵BE∥DG，点E是AD的点，∴AB=BG；∵CD∥FG，CD∥AG，∴四边形CDGF是平行四边形，∴CD=FG；‎ ‎∵∠ABE=∠EBC ，BE∥CF，∴∠EBC=∠BCF，∠ABE=∠BFC，∴BC=BF，‎ ‎∴AB-CD=BG-FG=BF=BC，∴AB=BC+CD.‎ 当AE=AD ()时，（）AB=BC+CD.‎