中考数学实数复习

中考数学实数复习

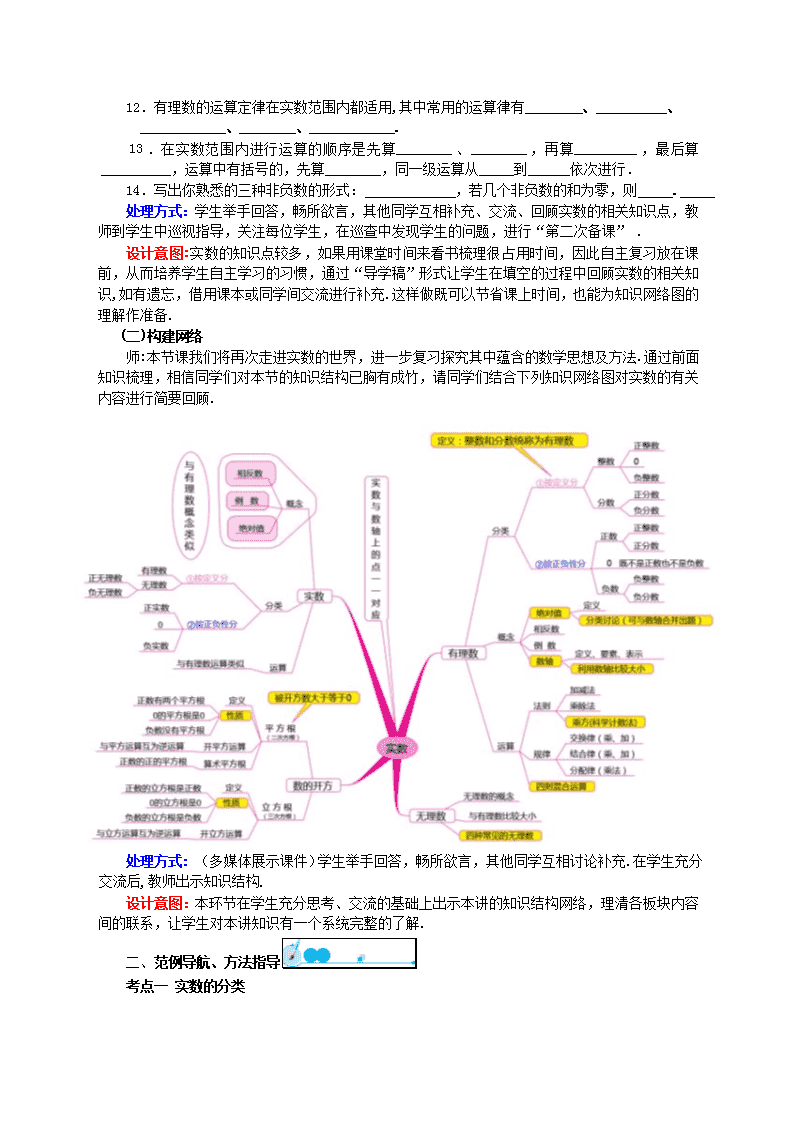
课题：第一讲 实数 ‎ 教学目标:‎ ‎1．了解有理数、无理数和实数的概念，知道实数与数轴上的点一一对应．‎ ‎2．借助数轴理解相反数和绝对值的意义，会求一个数的相反数、倒数与绝对值．‎ ‎3．了解平方根、算术平方根、立方根的概念，会用根号表示数的平方根、立方根．‎ ‎4．了解科学记数法、近似数与有效数字的概念，能按要求用四舍五入法求一个数的近似值，能正确识别一个数的有效数字的个数．在解决实际问题中，能用计算器进行近似计算，并按问题的要求对结果取近似值．‎ ‎5．熟练掌握实数的运算，会用各种方法比较两个实数的大小．‎ 教学重点与难点：‎ 重点：会运用运算规律，按照规定的运算法则进行实数的加、减、乘、除、乘方、开方混合运算.‎ 难点：掌握数学思想，熟练应用各个知识点解题．‎ 课前准备：教师制作多媒体课件．‎ 教学过程：‎ 一、 知识梳理，构建网络 ‎(一)知识梳理 师:课前请同学们翻阅课本并回忆实数的有关内容，熟记概念、性质等知识点，完成了知识梳理.下面我们比一比看看谁做得最好（导学稿，提前下发，学生在导学稿中填空.）‎ 处理方式：学生边口答边在导学稿中填空，师生共同回顾矫正．‎ 考点一 实数的分类 ‎1. 统称为实数，一般地实数有两种分类（如图）‎ ‎ ‎ 考点二 ‎ 实数的有关概念 ‎2．数轴：规定了 、 、 的直线叫数轴．数轴上的点与 是一一对应．‎ ‎3．相反数：到原点的距离相等且符号不同的两个数称为相反数,实数的相反数是 ,零的相反数是 ，与互为相反数，则 ；‎ ‎4．绝对值：在数轴上，表示一个数的点到原点的距离叫这个数的绝对值．‎ ‎5．倒数：若实数不为０，则的倒数为 ，若，则与互为 ．‎ 考点三 近似数、有效数字和科学计数法 ‎6．科学记数法：将一个数记作a×10n，其中（1≤|a|＜10，n是整数）的记数方法叫做科学记数法．当原数的绝对值≥10时，n为正整数，n等于原数的 ；当原数的绝对值＜1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．‎ ‎7．有效数字：一个数从左边第一个 的数字起，到右边精确到的数位止，所有的数字都叫这个数的有效数字．‎ ‎8． 精确度的形式有两种：（１） ；（２） ，一个近似数四舍五入到哪一位，就说这个近似数精确到哪一位，用科学记数法表示数的有效数字位数，只看乘号前的部分．‎ 考点四 平方根、算术平方根、立方根 ‎9．若，则叫做的 ，记做 ；正数的平方根有 个，它们互为 ，０的平方根是 ,负数没有平方根，正数的正的平方根叫做 ，记做，０的算术平方根是０．‎ ‎10．若，则叫做的 ，记做 ；正数的立方根有１个正的立方根，０的立方根是０，负数的立方根是负数．‎ 考点五 实数的大小比较 ‎11．比较实数大小的一般方法：‎ ‎ (1)数轴比较法：将两数表示在数轴上，右边的点表示的数总比左边的点表示的数 ．‎ ‎(2)性质比较法：正数大于 ；负数小于 ；正数 一切负数；两个负数，绝对值大的数 ．‎ ‎(3)差值比较法：设a，b是两个任意实数，则：a－b＞0则___，如－<0,则<，如－=0,则___．‎ ‎ (4)倒数比较法：若＞，a＞0，b＞0，则a b．‎ ‎(5)平方比较法：∵由a＞b＞0，可得 ，∴可以把与的大小问题转化成比较a和b的大小问题．‎ 考点六 实数的运算 ‎12．有理数的运算定律在实数范围内都适用,其中常用的运算律有________、__________、____________、________、____________.‎ ‎13．在实数范围内进行运算的顺序是先算________、________，再算_________，最后算__________，运算中有括号的，先算________，同一级运算从_____到______依次进行．‎ ‎14．写出你熟悉的三种非负数的形式： ，若几个非负数的和为零，则 . ‎ 处理方式：学生举手回答，畅所欲言，其他同学互相补充、交流、回顾实数的相关知识点，教师到学生中巡视指导，关注每位学生，在巡查中发现学生的问题，进行“第二次备课” .‎ 设计意图:实数的知识点较多，如果用课堂时间来看书梳理很占用时间，因此自主复习放在课前，从而培养学生自主学习的习惯，通过“导学稿”形式让学生在填空的过程中回顾实数的相关知识,如有遗忘，借用课本或同学间交流进行补充.这样做既可以节省课上时间，也能为知识网络图的理解作准备.‎ ‎(二)构建网络 ‎ 师:本节课我们将再次走进实数的世界，进一步复习探究其中蕴含的数学思想及方法.通过前面知识梳理，相信同学们对本节的知识结构已胸有成竹，请同学们结合下列知识网络图对实数的有关内容进行简要回顾.‎ 处理方式: （多媒体展示课件）学生举手回答，畅所欲言，其他同学互相讨论补充.在学生充分交流后,教师出示知识结构. ‎ 设计意图：本环节在学生充分思考、交流的基础上出示本讲的知识结构网络，理清各板块内容间的联系，让学生对本讲知识有一个系统完整的了解.‎ ‎ 二、范例导航、方法指导 考点一 实数的分类 例1　(2013安顺)下列各数：3.14159， ，0.131131113…，－π，， 无理数的个数有( )‎ A．1个 B．2个 C．3个 D．4个 解析：无理数是无限不循环的小数，其中的无理数有：0.131131113…，－π，故选B．‎ 方法总结：对数的判断不能从形式上判断是有理数还是无理数,应先把它们化简后从结果上作判断,再根据无理数的四种类型：①开方开不尽的数，②某些三角函数值，③含有π的数，(4)特殊结构数来判断即可．‎ 跟踪练习：‎ ‎1．(2014合肥)实数π，，0，－1中，无理数是( )‎ A．π　　　　B．　　　　C．0　　　　D．－1 ‎ ‎2．(2014安庆)下列各数中，为负数的是( )‎ A．0 B．－‎2 C．1 D． 考点二 实数的有关概念 例2 （1）（ 2014珠海）﹣的相反数是　　．‎ ‎（2）（ 2014广西玉林市）3的倒数是　 ．‎ ‎（3）（（2014四川成都）计算：|﹣|=　 ．‎ ‎（4）（2014呼和浩特）实数a，b，c在数轴上对应的点如图所示，则下列式子中正确的是（　　）‎ A．ac＞bc B．|a﹣b|=a﹣b C．﹣a＜﹣b＜c D．﹣a﹣c＞﹣b﹣c 解析：（1）根据相反数的定义，只有符号不同的两个数是互为相反数，﹣的相反数为．（2）根据倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．3的倒数是．（3）根据负数的绝对值等于它的相反数．解：|﹣|=．（4）先根据各点在数轴上的位置比较出其大小，再对各选项进行分析即可．‎ 解：∵由图可知，a＜b＜0＜c，∴A、ac＜bc，故本选项错误；B、∵a＜b，‎ ‎∴a﹣b＜0，∴|a﹣b|=b﹣a，故本选项错误；C、∵a＜b＜0，∴﹣a＞﹣b，故本选项错误；D、∵﹣a＞﹣b，c＞0，∴﹣a﹣c＞﹣b﹣c，故本选项正确．故选D．‎ 方法总结 ：解决本类题的关键是弄清实数中的有关的概念，关于绝对值除了了解几何意义，还应理解“正数的绝对值是它本身，零的绝对值是零，负数的绝对值是它的相反数”的内涵．实数与数轴问题，熟知数轴上各点与实数是一一对应关系是解答此类题的关键．‎ 跟踪练习：‎ ‎3．(2014年黑龙江绥化)－2014是2014的(　　)‎ A．相反数 B．倒数 C．绝对值 D．算术平方根 ‎4．（2014湖北荆门）若（　　）×（﹣2）=1，则括号内填一个实数应该是（　　）‎ ‎ A． B．‎2 C．﹣2 D．﹣‎ ‎5．(2014蚌埠)在如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数分别是和－1，则点C所对应的实数是( )‎ A．1＋ B．2＋ C．2－1 D．2＋1‎ 考点三 近似数、有效数字和科学计数法 例3　（2014湖南衡阳）环境空气质量问题已经成为人们日常生活所关心的重要问题，我国新修订的《环境空气质量标准》中增加了PM2.5检测指标，“PM‎2.5”‎是指大气中危害健康的直径小于或等于2.5微米的颗粒物，2.5微米即‎0.0000025米．用科学记数法表示0.0000025为（　　）‎ ‎　 A．2.5×10﹣5 B．2.5×‎105 ‎C 2.5×10﹣6 D． 2.5×106‎ 解析：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ 解：0.000 0025=2.5×10﹣6；故选：C．‎ 方法总结 ：科学记数法一般表示的数较大或很小，所以解题时一定要仔细，确定n的值时，把大数的总位数减1即为n的值，较小的数表示时就数第1个有效数字前所有“‎0”‎的个数(含小数点前的那个“‎0”‎)即为n的值．本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．‎ 跟踪练习：‎ ‎6．近似数2.5万精确到__ __位．‎ ‎7．（ 2014广西玉林市）将6.18×10﹣3化为小数的是（　　）‎ A．0.000618 B．‎0.00618 C．0.0618 D．0.618‎ ‎8．(2014芜湖)餐桌上的一蔬一饭，舌尖上的一饮一酌，实属来之不易，舌尖上的浪费让人触目惊心．据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为( )‎ A．5×1010千克 B．50×109千克 C．5×109千克 D．0.5×1011千克 考点四 平方根、算术平方根、立方根 例4 (1) （2014年江苏南京）8的平方根是（　　）‎ ‎　 A．4 B．±‎4 C． 2 D． ‎ ‎（2）（2014山东威海）若a3=8，则a的绝对值是 ．‎ 解析：（1）直接根据平方根的定义进行解答即可解决问题．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．‎ 解：∵，∴8的平方根是．故选D．‎ ‎（2）运用开立方的方法求解，关键是确定符号．解：∵a3=8，∴a=2． ‎ 方法总结 ：1．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．2．对于算术平方根，要注意：(1)一个正数只有一个算术平方根，它是一个正数；(2)0的算术平方根是0；(3)负数没有算术平方根；(4)算术平方根具有双重非负性：①被开方数a是非负数，即a≥0；②算术平方根本身是非负数，即≥0．3．()3＝a，＝a．‎ 跟踪练习：‎ ‎9．(2014陕西)4的算术平方根是（　　）‎ ‎　 A．﹣2 B． ‎2 C．±2 D． 16‎ 考点五 实数的大小比较 例5 （1）（2014益阳）四个实数﹣2，0，﹣，1中，最大的实数是（　　）‎ A．﹣2 B．‎0 C．﹣ D．1‎ ‎ (2)(2014河北)a，b是两个连续整数，若a＜＜b，则a，b分别是( )‎ A．2，3 B．3，‎2 C．3，4 D．6，8‎ 解析：（1）根据正数大于0，0大于负数，正数大于负数，比较即可．‎ 解：∵﹣2＜﹣＜0＜1，∴四个实数中，最大的实数是1．故选D．.‎ ‎（2），所以a=2，b=3‎ 方法总结：本题考查了实数大小比较，关键要熟记：正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小． 实数的各种比较方法，要明确应用条件及适用范围． ‎ 跟踪练习：‎ ‎10．（2014年江苏南京）下列无理数中，在﹣2与1之间的是（　　）‎ ‎　 A．﹣ B．﹣ C． D． ‎ ‎11．（2014新疆）规定用符号[x]表示一个实数的整数部分，例如[3.69]=3．[]=1，按此规定，[﹣1]=　 　．‎ 考点六 实数的运算 例6　（2014湖北黄石）计算：|﹣5|+2cos30°+（）﹣1+（9﹣）0+．‎ 解析：先分别算出每一项的值，然后根据实数的运算法则求得计算结果．‎ ‎ 解：原式==11．‎ 方法总结：实数运算的考查是中考的必考知识, 此类题中常常结合绝对值、零指数、负指数、特殊角的三角函数值、无理数的化简等概念，牢记这些概念是解决这类问题的关键．解题时还应注意运算顺序以及运算技巧． ‎ 跟踪练习：‎ ‎12．（2014浙江金华）计算：‎ ‎13．(2014东营)计算：(－1)2014＋(sin30°)－1＋()0－|3－|＋83×(－0.125)3.‎ 考点七 实数非负性质的应用 例7 （2014河北）若实数m，n 满足|m﹣2|+（n﹣2014）2=0，则m﹣1+n0=　 ．‎ 解析：根据绝对值与平方的和为0，可得绝对值与平方同时为0，根据负整指数幂、非0的0次幂，可得答案．‎ 解：|m﹣2|+（n﹣2014）2=0，m﹣2=0，n﹣2014=0，m=2，n=2014．‎ m﹣1+n0=2﹣1+20140=+1=，故答案为：．‎ 方法总结：中考中对于非负数考查也比较多,这就需要学生掌握非负数的性质及几4种形式.常见的非负数的形式有三种：|a|，(a≥0)，a2，若它们的和为零，则每一个式子都为0．‎ 跟踪练习：‎ ‎14．（2014四川泸州）已知实数x、y满足+|y+3|=0，则x+y的值为（　　）‎ A．-2 B．‎2 C．4 D．﹣4‎ 处理方式：以上例题及练习都是基础知识和基本技能的再现，学生自主完成练习，教师各小组巡视.完成后先由学生相互补充、交流、评价．教师适时进行有针对性的提问并指导学生总结归纳知识点和方法，反馈矫正，做到查缺补漏．例6让两名学生主动到黑板板演，其他学生在练习本上完成．教师巡视，适时点拨．学生完成后及时点评，借助多媒体展示学生出现的问题进行矫正．‎ 设计意图：本环节设计七个有代表性的关于实数的典型考题，让学生在练习的过程中体会每种类型题解题的关键. 同时学生通过练习，自查补漏，发现问题及时解决．在解决问题的过程中掌握方法、学会学习.‎ ‎ 三、回顾反思，提炼升华 通过本节课的复习，你有哪些收获？有何感想？学会了哪些方法？先想一想，再分享给大家．‎ 学生畅谈自己的收获！‎ 设计意图：课堂总结是知识沉淀的过程，使学生对本节课所学进行梳理，养成反思与总结的习惯，培养自我反馈，自主发展的意识．同时在与同学交流的过程中，增强与他人合作的意识.‎ 四、达标测试，反馈提高 ‎1．(2014年山东东营)的平方根是（　　）‎ ‎　 A．±3 B． ‎3 C．±9 D． 9‎ ‎2．（2014德州）下列计算正确的是（　　）‎ A．﹣（﹣3）2=9 B．=‎3 C．﹣（﹣2）0=1 D．|﹣3|=﹣3‎ ‎3．（2014山东潍坊）下列实数中是无理数的是( )‎ ‎ A． 　　　 B．2－‎2 ‎ 　　　C．　 　 D．sin450‎ ‎4．(2014年广东深圳)支付宝与“快的打车”联合推出优惠，“快的打车”一夜之间红遍大江南北．据统计，2014年“快的打车”账户流水总金额达到47.3亿元.47.3亿用科学记数法表示为(　　)‎ A．4.73×108 B．4.73×‎109 C．4.73×1010 D．4.73×1011‎ ‎5．（2014湖北宜昌）如图，M，N两点在数轴上表示的数分别是m，n，下列式子中成立的是（　　）‎ A．m+n＜0 B．﹣m＜﹣n C．|m|﹣|n|＞0 D．2+m＜2+n ‎ ‎6．（2014山东临沂）一般地，我们把研究对象统称为元素，把一些元素组成的总体称为集合．一个给定集合中的元素是互不相同的，也就是说，集合中的元素是不重复出现的．如一组数1，1，2，3，4就可以构成一个集合，记为A={1，2，3，4}．类比实数有加法运算，集合也可以“相加”．定义：集合A与集合B中的所有元素组成的集合称为集合A与集合B的和，记为A+B．若A={﹣2，0，1，5，7}，B={﹣3，0，1，3，5}，则A+B=　 ‎ ‎7．(2014年广东深圳)计算：－2tan60°＋(－1)0－－1 ‎ 处理方式：学生用6分钟独立完成，然后反馈矫正.对于出错较多的题目重点讲解. ‎ 设计意图：限时训练 ，一方面可以了解学生对本节课所复习内容的掌握情况， 同时也可以培养学生快速准确解决问题的能力.每一道小题都各有目的，从不同的侧面考查了这节的知识点，从而达到熟练应用知识的目的．‎ 五、布置作业，课堂延伸 必做题：完成复习指导丛书第4 页到7页内容．‎ 选做题：1．(2014年四川达州)《庄子·天下篇》中写道：“一尺之棰，日取其半，万世不竭”意思是：一根一尺的木棍，如果每天截取它的一半，永远也取不完，如图 由图易得：＋＋＋…＋＝________.‎ ‎2．（2014甘肃兰州）为了求1+2+22+23+…+2100的值，可令S=1+2+22+23+…+2100，则2S=2+22+23+24+…+2101，因此2S﹣S=2101﹣1，所以S=2101﹣1，即1+2+22+23+…+2100=2101﹣1，仿照以上推理计算1+3+32+33+…+32014的值是 ．‎ 板书设计：‎ 第一讲 实数 ‎1．知识梳理 ‎2．范例导航 考点一：实数的分类 考点二：实数的有关概念 考点三：科学记数法与近似数、有效数字 考点四：平方根、算术平方根、立方根 考点五：实数的大小比较 考点六：实数的运算 考点七：实数非负性质的应用 投 影 区 学 生 活 动 区