中考数学热点探索规律

中考数学热点探索规律

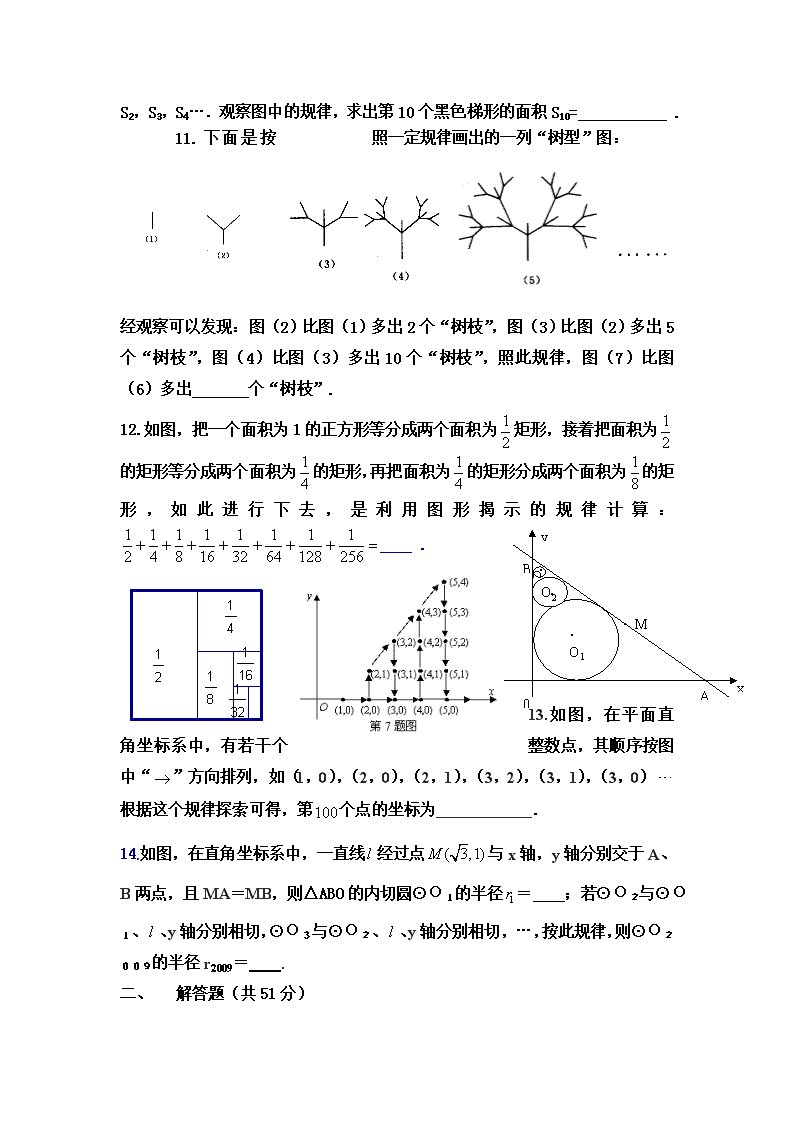
中考热点：探索规律专项训练 一、 选择题(每题3分，共21分)‎ ‎1.如图，是一个装饰物品连续旋转闪烁所成的三个图形，照此规律闪烁，下一个呈现出来的图形是（ ）.‎ ‎(第1题图)‎ A B C D ‎2.为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：‎ 按照上面的规律，摆个“金鱼”需用火柴棒的根数为（ ）A A． B． C． D．‎ ‎3.小王利用计算机设计了一个计算程序，输入和输出的数据如下表：‎ 输入 ‎…‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎…‎ 输出 ‎…‎ ‎…‎ ‎ 那么，当输入数据是8时，输出的数据是 （ ）‎ ‎ A. B. C. D. ‎ ‎4.图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成，按照这样的规律继续叠放下去，至第七个叠放的图形中，小正方体木块总数应是（ ）‎ A.25 B. ‎66 C . 91 D. 120‎‎（第18题）‎ A1‎ A2‎ A3‎ A4‎ ‎5．如图，将n个边长都为‎1cm的正方形按如图所示摆放，点A1、A2、…、An分别是正方形的中心，则n个这样的正方形重叠部分的面积和为（ ）‎ A．cm2 B．cm‎2 C．cm2 D． cm2‎ ‎6.如图，小明作出了边长为1的第1个正△A1B‎1C1，算出了正△A1B‎1C1的面积.然后分别取△A1B‎1C1的三边中点A2、B2、C2，作出了第2个正△A2B‎2C2，算出了正△A2B‎2C2的面积.用同样的方法，作出了第3个正△A3B‎3C3，算出了正△A3B‎3C3的面积……，由此可得，第10个正△A10B‎10C10的面积是（　） ‎ A． B． C． D．　　‎ ‎7．《九章算术》是我国东汉初年编订的一部数学经典著作．在它的图3－2‎ 图3－1‎ “方程”一章里，一次方程组是由算筹布置而成的．《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图3－1、图3－2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图3－1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是类似地，图3－2所示的算筹图我们可以表述为 ( )‎ A． B． C． D．‎ 二、填空题（每题4分，共28分）‎ ‎8.观察下面的单项式：a，‎-2a2，‎4a3，‎-8a4，…．根据你发现的规律，第n(n≥1的整数 个式子是____．‎ ‎9.观察下列各式：‎ 请你将发现的规律用含自然数n(n≥1)的等式表示出来 ． ‎ ‎10.如图4，∠AOB=45°，过OA上到点O的距离分别为1，3，5，7，9，11…的点作OA的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为S1‎ ‎，S2，S3，S4…．观察图中的规律，求出第10个黑色梯形的面积S10=　　　　　 .‎ ‎ 11.下面是按照一定规律画出的一列“树型”图：‎ ‎ 经观察可以发现：图（2）比图（1）多出2个“树枝”，图（3）比图（2）多出5个“树枝”，图（4）比图（3）多出10个“树枝”，照此规律，图（7）比图（6）多出 个“树枝”.‎ ‎0‎ x y A B M O1‎ O2‎ O3‎ ‎12.如图，把一个面积为1的正方形等分成两个面积为矩形，接着把面积为的矩形等分成两个面积为的矩形，再把面积为的矩形分成两个面积为的矩形，如此进行下去，是利用图形揭示的规律计算： .‎ ‎13.如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“”方向排列，如（1，0），（2，0），（2，1），（3，2），（3，1），（3，0）根据这个规律探索可得，第个点的坐标为____________． ‎ ‎14.如图，在直角坐标系中，一直线经过点与x轴，y轴分别交于A、B两点，且MA＝MB，则△ABO的内切圆⊙Ｏ１的半径＝ ；若⊙Ｏ２与⊙Ｏ１、、y轴分别相切，⊙Ｏ３与⊙Ｏ２、、y轴分别相切，…，按此规律，则⊙Ｏ２００９的半径r2009＝ .‎ 一、 解答题（共51分）‎ ‎15.（8分）.已知△ABC内接于⊙O，过点A作直线EF.‎ ‎（1）如图①，AB是直径，要使EF是⊙O的切线，还要添加的条件是（只需要写出三种情况）‎ ‎① ，或② ，或③ .‎ ‎（2）如图②，AB为非直径的弦，∠EAB=∠B,试证明EF是⊙O的切线.‎ ‎16.（10分）在如图12－1至图12－3中，△ABC的面积为a ．‎ ‎（1）如图12－1， 延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S1，则S1=________（用含a的代数式表示）；‎ A B C D E 图12－2‎ D E A B C F 图12－3‎ ‎（2）如图12－2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2，则S2=__________（用含a的代数式表示），并写出理由；‎ 图12－1‎ A B C D ‎   （3）在图12－2的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图12－3）．若阴影部分的面积为S3，则S3=__________（用含a的代数式表示）．‎ 图12－4‎ D E A B C F H M G 发现 像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF（如图12－3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的_______倍．‎ 应用 去年在面积为‎10m2‎的△ABC空地上栽种了某种花卉．今年准备扩大种植规模，把△ABC向外进行两次扩展，第一次由△ABC扩展成△DEF，第二次由△DEF扩展成△MGH（如图12－4）．求这两次扩展的区域（即阴影部分）面积共为多少m2？‎ ‎17.（10分）已知等边△OAB的边长为a，以AB边上的高OA1 为边，按逆时针方向作等边△OA1B1，A1B1与OB相交于点A2. ‎ ‎（1）求线段OA2的长；‎ ‎（2）若再以OA2为边按逆时针方向作等边△OA2B2，‎ A2B2与OB1相交于点A3，按此作法进行下去，得到 ‎△OA3B3，△OA4B4，┉，△OAnBn，（如图），‎ 求△OA6B6，的周长.‎ ‎18.（10分）、如图①、②、③中，点E、D分别是正△ABC、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点，且BE = CD，DB交AE于P点．‎ ‎⑴求图①中，∠APD的度数；‎ ‎⑵图②中，∠APD的度数为___________，图③中，∠APD的度数为___________；‎ ‎⑶根据前面探索，你能否将本题推广到一般的正n 边形情况．若能，写出推广问题和结论；若不能，请说明理由．‎ ‎19.（13分）、操作：如图①，△ABC是正三角形，△BDC是顶角∠BDC＝120°的等腰三角形，以D为顶点作一个60°角，角的两边分别交AB、AC边于M、N两点，连接MN．‎ 探究：(1)线段BM、MN、NC之间的关系，并加以证明．‎ ‎(2)若点M、N分别是射线AB、CA上的点，其它条件不变，再探线段BM、MN、NC之间的关系，在图④中画出图形，并说明理由．　　‎ ‎ ‎ 附答案：‎ ‎1.B 2.A 3.C 4.C 5.C 6.A 7.A 8. 9. ‎ ‎10.76 解析：阴影部分的面积=上+下 ，上=4n+1 ，下=4n+3 (n≥0的整数)‎ 当n=9时，上=37，下=39 ∴S10=37+39=76‎ ‎11．80．‎ 图（2）比图（1）多：2=21 ； 图（3）比图（2）多：22+1=22+2；‎ 图（4）比图（3）多：23+21； 图（5）比图（4）多：24+22；‎ 图（6）比图（5）多：25+23； 图（7）比图（6）多：26+24‎ ‎12． ‎ 解析：1-.‎ ‎13.（14，8）‎ 解析：从两方面考虑：①从每一列坐标个数分析： 第一列：1个；第二列2个；第三列3个；第四列5个；……，第十三列有13个.1至13列共有：.‎ ‎②横坐标是偶数时上升，横坐标是奇数时下降.第100个数横坐标是14，应上升，纵坐标应是第9个数，坐标应为（14，8）.‎ ‎14. ‎ 解析：如图13-1‎ tan∠MOA=, ∴∠MOA=300 ∴∠BAO=300‎ ‎∴OM=AM=2 ∴AB=4,OB=2 ,OA=‎ ‎∴ ∴‎ 如图13-2‎ 在Rt△O1O2M中， ∠O1O2M=300 ‎ ‎∴O1O2=2O‎1M ∴‎ ‎∴ 同理： ∴ …‎ ‎∴‎ ‎15.解析：（1）①∠CAE=∠B,②AB⊥EF,③∠BAC+∠CAE=900‎ ‎④∠C=∠FAB⑤∠EAB=∠FAB ‎(2)连结AO,并延长交⊙O于H，连结HC,‎ ‎∵AH是⊙O的直径，∴∠H+∠HAC=900.‎ ‎∵∠H=∠B,∠EAC=∠B,∴∠H=∠CAE ‎ ‎∴∠EAC+∠HAC=900,∴HA⊥EF ∴EF是⊙O的切线.‎ ‎16. 探索 ‎（1）a （2）‎2a ‎ 理由：∵CD=BC，AE=CA，BF=AB ‎ ‎∴由（2）得 S△ECD=‎2a，S△FAE=‎2a，S△DBF=‎2a，‎ ‎∴S3=‎6a． ‎ ‎（3）‎6a ； 7． ‎ ‎（72－7）×10=420（平方米）；或10=420（平方米）.‎ ‎ ‎ ‎17.‎ ‎ ‎ ‎18.解：（1）∵△ABC是等边三角形 ∴AB=BC，∠ABE=∠BCD=60°‎ ‎∵BE=CD ∴△ABE≌△BCD ∴∠BAE=∠CBD ‎ ‎∴∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60° ‎ ‎（2）90°，108° ‎ ‎（3）能．如图，点E、D分别是正n边形ABCM …中以C点为顶点的相邻两边上的点，且BE=CD，BD与AE交于点P，则∠APD的度数为 ‎19、解：BM＋CN＝MN ‎ 证明：如图，延长AC至M1，使CM1＝BM，连结DM1 ‎ ‎∵△ABC为等边三角形，∴∠ABC＝∠ACB＝60°，‎ ‎∵∠BDC=1200 BD=DC ∴∠DBC＝∠DCB＝30°‎ ‎∴∠ABD＝∠ACD＝90°∴∠DCM=900 ∵BD＝CD ‎ ‎△∴Rt△BDM≌Rt△CDM1 ‎ ‎∴∠MDB＝∠M1DC　　DM＝DM1 ‎ ‎∴∠MDM1＝（120°－∠MDB）＋∠M1DC＝120° ‎ ‎ 又∵∠MDN＝60°‎ ‎∴∠M1DN＝∠MDN＝60° ∴△MDN≌△M1DN ‎ ‎∴MN＝NM1＝NC＋CM1＝NC＋MB ‎ ‎（2） CN－BM＝MN 证明：如图，在CN上截取 CM1＝BM，连结DM1 ‎ ‎∵△ABC为等边三角形，∴∠ABC＝∠ACB＝60°，‎ ‎∵∠BDC=1200 BD=DC ‎∴∠DBC＝∠DCB＝30°‎ ‎∴∠DBM＝∠DCM1＝90°‎ ‎∵BD＝CD ‎∴Rt△BDM≌Rt△CDM1‎ ‎∴∠MDB＝∠M1DC　　DM＝DM1 ‎ ‎∵∠BDM＋∠BDN＝60°∴∠CDM1＋∠BDN＝60°‎ ‎∴∠NDM1＝∠BDC－（∠M1DC＋∠BDN）＝120°－60°＝60°‎ ‎∴∠M1DN＝∠MDN ∵ND＝ND ‎∴△MDN≌△M1DN ∴MN＝NM1＝NC－CM1＝NC－MB ‎ ‎ ‎ ‎.‎