2009年山东省东营市中等学校招生考试数学试题及答案

2009年山东省东营市中等学校招生考试数学试题及答案

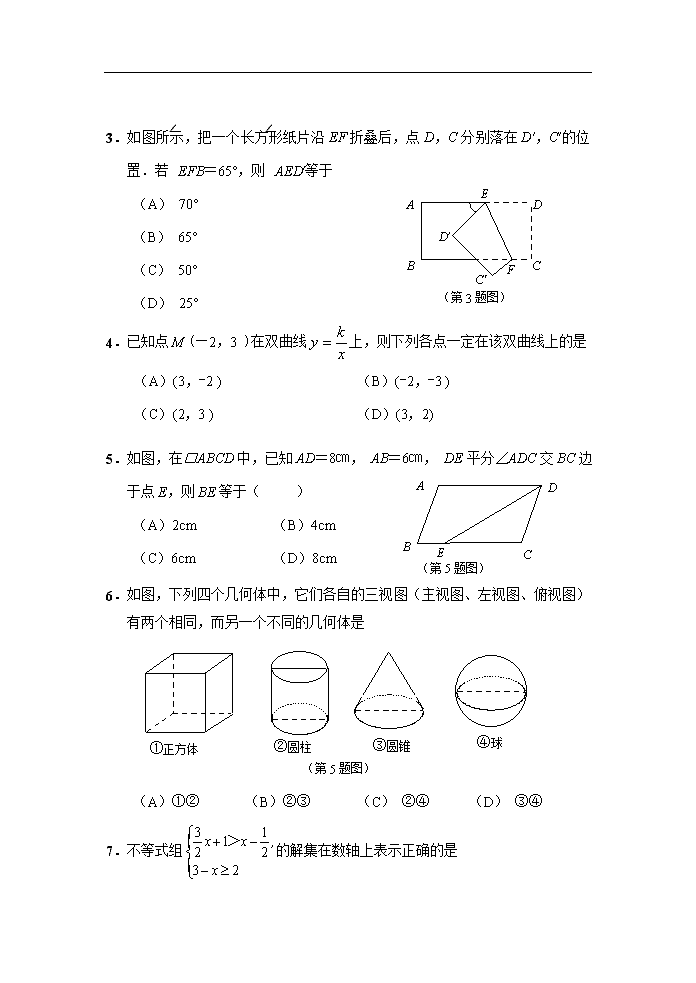
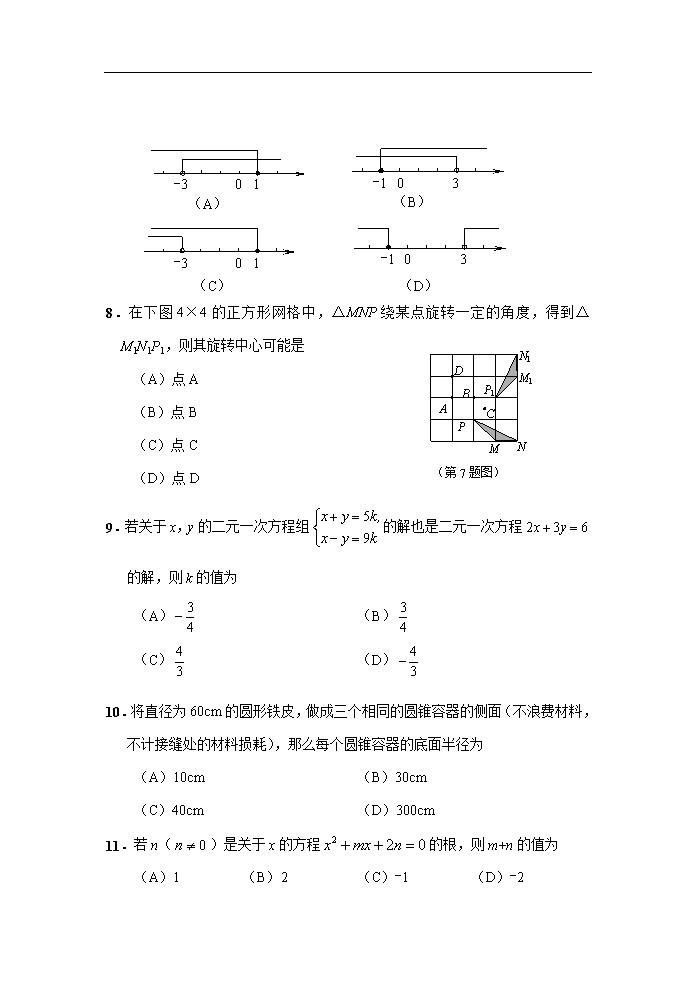
绝密★启用前 试卷类型:A ‎ 山东省东营市二○○九年中等学校招生考试 ‎ 数 学 试 题 ‎ 注意事项： ‎ ‎1．本试题分第Ⅰ卷和第Ⅱ卷两部分．第Ⅰ卷4页为选择题，36分；第Ⅱ卷8页为非选择题，84分；全卷共12页，满分120分，考试时间为120分钟．‎ ‎2．答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目涂写在答题卡上，考试结束，试题和答题卡一并收回． ‎ ‎3．第Ⅰ卷每题选出答案后，必须用2B铅笔把答题卡上对应题目的答案标号【ABCD】涂黑．如需改动，先用橡皮擦干净，再改涂其它答案． ‎ 第Ⅰ卷（选择题 共36分） ‎ 一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来．每小题选对得3分，选错、不选或选出的答案超过一个均记零分． ‎ ‎1．某市2009年元旦的最高气温为‎2℃‎，最低气温为－‎8℃‎，那么这天的最高气温比最低气温高 ‎ ‎（Ａ）‎-10℃‎ （Ｂ）-6℃ ‎ ‎（Ｃ）‎6℃‎ （Ｄ）‎10℃‎ ‎ ‎2．计算的结果是 ‎ ‎（Ａ） （B） ‎ ‎（C） 　 （D） ‎ E D B C′‎ F C D′‎ A ‎（第3题图）‎ ‎3．如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠EFB＝65°，则∠AED′等于 ‎ ‎（A） 70° ‎ ‎（B） 65° 　 ‎ ‎（C） 50° ‎ ‎（D） 25° ‎ ‎4．已知点M (－2，3 )在双曲线上，则下列各点一定在该双曲线上的是 ‎（A）(3，-2 ) （B）(-2，-3 ) ‎ ‎（C）(2，3 ) （D）(3，2) ‎ A B C D ‎（第5题图）‎ E ‎5．如图，在□ABCD中，已知AD＝8㎝， AB＝6㎝， DE平分∠ADC交BC边于点E，则BE等于（ ） ‎ ‎（A）‎2cm （B）‎4cm ‎ ‎（C）‎6cm （D）‎8cm ‎ ‎6．如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）有两个相同，而另一个不同的几何体是 ‎ ‎①正方体 ‎②圆柱 ‎③圆锥 ‎④球 ‎（第5题图）‎ ‎（A）①② （B）②③ （C） ②④ （D） ③④ ‎ ‎7．不等式组的解集在数轴上表示正确的是 ‎（A）‎ ‎-3‎ ‎1‎ ‎0‎ ‎（B）‎ ‎-1‎ ‎3‎ ‎0‎ ‎（C）‎ ‎-3‎ ‎1‎ ‎0‎ ‎（D）‎ ‎-1‎ ‎3‎ ‎0‎ A B C D M N P P1‎ M1‎ N1‎ ‎（第7题图）‎ ‎8．在下图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是 ‎ ‎（A）点A ‎ ‎（B）点B ‎ ‎（C）点C ‎ ‎（D）点D ‎ ‎9．若关于x，y的二元一次方程组的解也是二元一次方程 的解，则k的值为 ‎ ‎（A） （B） ‎ ‎（C） （D） ‎ ‎10．将直径为‎60cm的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为 ‎ ‎（A）‎10cm （B）‎30cm ‎ ‎（C）‎40cm （D）‎300cm ‎ ‎11．若n（）是关于x的方程的根，则m+n的值为 ‎ ‎（A）1 （B）2 （C）-1 （D）-2 ‎ y x O B A ‎（第12题图）‎ ‎12．如图，点A的坐标为(－1，0)，点B在直线y=x上运动，当线段AB最短时，点B的坐标为 ‎ ‎（A）（0，0） ‎ ‎（B）（，） ‎ ‎（C）（－，－） ‎ ‎（D）（－，－） ‎ 绝密★启用前 试卷类型:A ‎ 山东省东营市二○○九年中等学校招生考试 数 学 试 题 ‎ 第Ⅱ卷（非选择题 共84分）‎ 注意事项：‎ ‎　1．第Ⅱ卷共8页，用钢笔或圆珠笔直接写在试卷上．‎ ‎2．答卷前将密封线内的项目填写清楚．‎ 题号 二 三 总分 ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得分 得 分 评 卷 人 二、填空题：本大题共5小题，共20分，只要求填写最后结果，每小题填对得4分．‎ ‎13．‎2009年4月16日，国家统计局发布：一季度，城镇居民人均可支配收入为4834元，与去年同时期相比增长10.2%．4838元用科学记数法表示为 ． ‎ ‎14．甲、乙两位棉农种植的棉花，连续五年的单位面积产量（千克/亩）统计如下表，则产量较稳定的是棉农_________________． ‎ 棉农甲 ‎68‎ ‎70‎ ‎72‎ ‎69‎ ‎71‎ 棉农乙 ‎69‎ ‎71‎ ‎71‎ ‎69‎ ‎70‎ ‎15．如图，在四边形ABCD中，已知AB与CD不平行，∠ABD＝∠ACD ‎，请你添加一个条件： ，使得加上这个条件后能够推出AD∥BC且AB＝CD. ‎ B C D A O ‎（第15题图）‎ E ‎（第16题图）‎ A B′‎ C F B ‎16．将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，那么BF的长度是 ． ‎ y x O C1‎ B2‎ A2‎ C3‎ B1‎ A3‎ B3‎ A1‎ C2‎ ‎（第17题图）‎ ‎17．正方形A1B‎1C1O，A2B‎2C2C1，A3B‎3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分 别在直线(k＞0)和x轴 上，已知点B1(1，1)，B2(3，2)， ‎ 则Bn的坐标是______________．‎ 三、解答题：本大题共7小题，共64分．解答要写出必要的文字说明、证明过程或演算步骤． ‎ 得 分 评 卷 人 ‎18． (本题满分7分) ‎ 化简：． ‎ 得 分 评 卷 人 ‎19． (本题满分9分) ‎ 某中学对全校学生60秒跳绳的次数进行了统计，全校平均次数是100次．某班体育委员统计了全班50名学生60秒跳绳的成绩，列出的频数分布直方图如下（每个分组包括左端点，不包括右端点）：‎ 求：（1）该班60秒跳绳的平均次数至少是多少？是否超过全校平均次数？‎ ‎（2）该班一个学生说：“我的跳绳成绩在我班是中位数”，请你给出该生跳绳成绩的所在范围．‎ ‎（3）从该班中任选一人，其跳绳次数达到或超过校平均次数的概率是多少？‎ ‎（第19题图）‎ ‎60‎ ‎80‎ ‎100‎ ‎120‎ ‎140‎ ‎160‎ ‎180‎ 次数 ‎4‎ ‎2‎ ‎5‎ ‎7‎ ‎13‎ ‎19‎ 频数 O ‎ ‎ 得 分 评 卷 人 ‎20． (本题满分9分) ‎ A C D E B O ‎（第20题图）‎ l 如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点 E． ‎ ‎ (1) 求∠AEC的度数； ‎ ‎（2）求证：四边形OBEC是菱形． ‎ C A ‎ ‎ 得 分 评 卷 人 ‎21． (本题满分9分)‎ 为了贯彻落实国务院关于促进家电下乡的指示精神，有关部门自2007年12月底起进行了家电下乡试点，对彩电、冰箱（含冰柜）、手机三大类产品给予产品销售价格13%的财政资金直补．企业数据显示，截至2008年12月底,试点产品已销售350万台（部），销售额达50亿元，与上年同期相比，试点产品家电销售量增长了40%． ‎ ‎（1）求2007年同期试点产品类家电销售量为多少万台（部）？ ‎ ‎（2）如果销售家电的平均价格为：彩电每台1500元，冰箱每台2000元，手机每部800元，已知销售的冰箱（含冰柜）数量是彩电数量的倍，求彩电、冰箱、手机三大类产品分别销售多少万台（部），并计算获得的政府补贴分别为多少万元？ ‎ 得 分 评 卷 人 ‎22． (本题满分10分)‎ 如图，斜坡AC的坡度（坡比）为1:，AC＝‎10米．坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB＝‎14米．试求旗杆BC的高度． ‎ A B C ‎（第22题图）‎ D 得 分 评 卷 人 ‎23． (本题满分10分) ‎ 某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=‎2米，BC=‎1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN 是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆． ‎ ‎（1）当MN和AB之间的距离为‎0.5米时，求此时△EMN的面积； ‎ ‎（2）设MN与AB之间的距离为米，试将△EMN的面积S（平方米）表示成关于x的函数； ‎ E A B G N D M C ‎（第23题图）‎ ‎（3）请你探究△EMN的面积S（平方米）有无最大值，若有，请求出这个最大值；若没有，请说明理由． ‎ 得 分 评 卷 人 ‎24． (本题满分10分) ‎ 已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．‎ ‎（1）求证：EG=CG；‎ ‎（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由． ‎ F B A D C E G 第24题图①‎ ‎（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）‎ ‎ ‎ F B A D C E G 第24题图②‎ F B A C E 第24题图③‎ D 山东省东营市二○○九年中等学校招生考试 数学试题参考解答及评分意见 评卷说明：‎ ‎1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．本答案对每小题只给出一种或两种解法，对考生的其他解法，请参照评分意见进行评分．‎ ‎3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．‎ 一、选择题：(本大题共12小题，每小题3分，共36分)‎ 题号 1 2 3 4 5 6 7 8 9 10 11 12‎ 答案 D D C A A B A B B A D C 二、填空题：(本大题共5小题，每小题4分，共20分)‎ ‎13．4.834×103； 14．乙； ‎ ‎15．∠DAC＝∠ADB，∠BAD＝∠CDA，∠DBC＝∠ACB，∠ABC＝∠DCB，OB＝OC，OA＝OD；(任选其一) ‎ ‎16． 或2; 17． ． ‎ 三、解答题：(本大题共7小题, 共64分)‎ ‎18．(本小题满分6分) ‎ 解：原式= o ………………………1分 ‎ = o ………………………4分 ‎ = …………………………………………6分 ‎ = =1. ……………………………………………7分 ‎19．(本小题满分9分) ‎ 解：（1）该班60秒跳绳的平均次数至少是： ＝100.8．‎ 因为100.8>100，所以一定超过全校平均次数． …………………3分 ‎（2）这个学生的跳绳成绩在该班是中位数，由4+13+19=36，所以中位数一定在100～120范围内． …………………………………………6分 ‎（3）该班60秒跳绳成绩大于或等于100次的有：19+7+5+2=33（人），‎ ‎……………………………………………………………………………8分 ‎ ．所以，从该班任选一人，跳绳成绩达到或超过校平均次数的概率为0.66． ………………………………………………………… 9分 ‎20．(本题满分9分)‎ ‎（1）解：在△AOC中，AC=2，‎ ‎ ∵ AO＝OC＝2，‎ ‎∴ △AOC是等边三角形．………2分 ‎∴ ∠AOC＝60°， ‎ ‎∴∠AEC＝30°．…………………4分 ‎（2）证明：∵OC⊥l，BD⊥l． ‎ ‎∴ OC∥BD． ……………………5分 ‎∴ ∠ABD＝∠AOC＝60°．‎ ‎∵ AB为⊙O的直径，‎ ‎∴ △AEB为直角三角形，∠EAB＝30°． …………………………7分 ‎ ∴∠EAB＝∠AEC． ‎ ‎ ∴ 四边形OBEC 为平行四边形． …………………………………8分 ‎ 又∵ OB＝OC＝2． ‎ ‎ ∴ 四边形OBEC是菱形． …………………………………………9分 ‎21．(本题满分9分)‎ 解：（1）2007年销量为a万台，则a(1+40%)=350，a =250（万台）． ‎ ‎…………………………………………………………………………3分 ‎（2）设销售彩电x万台，则销售冰箱 x万台，销售手机(350- x)万台．由题意得：1500x+2000× +800(350 x)=500000． ……………6分 解得x＝88． ………………………………………………………7分 ‎∴ ， ． ‎ 所以，彩电、冰箱（含冰柜）、手机三大类产品分别销售88万台、132万台、130万部．………………………………………………………………8分 ‎∴ 88×1500×13%=17160（万元），132×2000×13%=34320（万元），‎ ‎130×800×13%=13520（万元）． ‎ 获得的政府补贴分别是17160万元、34320万元、13520万元． ……9分 ‎22．（本题满分10分）‎ 解：延长BC交AD于E点，则CE⊥AD．……1分 在Rt△AEC中，AC＝10， ‎ 由坡比为1: 可知：∠CAE＝30°，………2分 ‎∴ CE＝AC·sin30°＝10× ＝5，………3分 AE＝AC·cos30°＝10× ＝ ．……5分 在Rt△ABE中，‎ BE＝ ＝ =11．……………………………8分 ‎∵ BE＝BC＋CE，‎ ‎∴ BC＝BE－CE＝11-5＝6（米）． ‎ 答：旗杆的高度为6米． …………………………………………10分 ‎23．（本题满分10分）‎ 解：（1）由题意，当MN和AB之间的距离为0.5米时，MN应位于DC下方，且此时△EMN中MN边上的高为0.5米.‎ 所以，S△EMN= =0.5（平方米）.‎ 即△EMN的面积为0.5平方米. …………2分 ‎（2）①如图1所示，当MN在矩形区域滑动，‎ 即0＜x≤1时， ‎ ‎△EMN的面积S= = ；……3分 ‎②如图2所示，当MN在三角形区域滑动，‎ 即1＜x＜ 时，‎ 如图，连接EG，交CD于点F，交MN于点H，‎ ‎∵ E为AB中点，‎ ‎∴ F为CD中点，GF⊥CD,且FG＝ .‎ 又∵ MN∥CD，‎ ‎∴ △MNG∽△DCG．‎ ‎∴ ，即 ．……4分 故△EMN的面积S＝ ‎ ‎＝ ； …………………5分 综合可得： ‎ ‎ ……………………………6分 ‎（3）①当MN在矩形区域滑动时， ，所以有 ；………7分 ‎②当MN在三角形区域滑动时，S= .‎ 因而，当 （米）时,S得到最大值，‎ 最大值S= = = （平方米）. ……………9分 ‎∵ ，‎ ‎∴ S有最大值，最大值为 平方米. ……………………………10分 ‎24．（本题满分10分）‎ 解：（1）证明：在Rt△FCD中， ‎ ‎∵G为DF的中点，‎ ‎∴ CG= FD．………………1分 同理，在Rt△DEF中， ‎ EG= FD． ………………2分 ‎∴ CG=EG．…………………3分 ‎（2）（1）中结论仍然成立，即EG=CG．…………………………4分 证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．‎ 在△DAG与△DCG中，‎ ‎∵ AD=CD，∠ADG=∠CDG，DG=DG，‎ ‎∴ △DAG≌△DCG．‎ ‎∴ AG=CG．………………………5分 在△DMG与△FNG中，‎ ‎∵ ∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，‎ ‎∴ △DMG≌△FNG．‎ ‎∴ MG=NG ‎ 在矩形AENM中，AM=EN． ……………6分 在Rt△AMG 与Rt△ENG中，‎ ‎∵ AM=EN， MG=NG，‎ ‎∴ △AMG≌△ENG．‎ ‎∴ AG=EG．‎ ‎∴ EG=CG． ……………………………8分 证法二：延长CG至M,使MG=CG，‎ 连接MF，ME，EC， ……………………4分 在△DCG 与△FMG中，‎ ‎∵FG=DG，∠MGF=∠CGD，MG=CG，‎ ‎∴△DCG ≌△FMG．‎ ‎∴MF=CD，∠FMG＝∠DCG． ‎ ‎∴MF∥CD∥AB．………………………5分 ‎∴ ．‎ 在Rt△MFE 与Rt△CBE中，‎ ‎∵ MF=CB，EF=BE，‎ ‎∴△MFE ≌△CBE．‎ ‎∴ ．…………………………………………………6分 ‎∴∠MEC＝∠MEF＋∠FEC＝∠CEB＋∠CEF＝90°． …………7分 ‎∴ △MEC为直角三角形．‎ ‎∵ MG = CG，‎ ‎∴ EG= MC．‎ ‎∴ ．………………………………8分 ‎（3）（1）中的结论仍然成立，‎ 即EG=CG．其他的结论还有:EG⊥CG．……10分