荆州市年016年中数学卷

荆州市年016年中数学卷

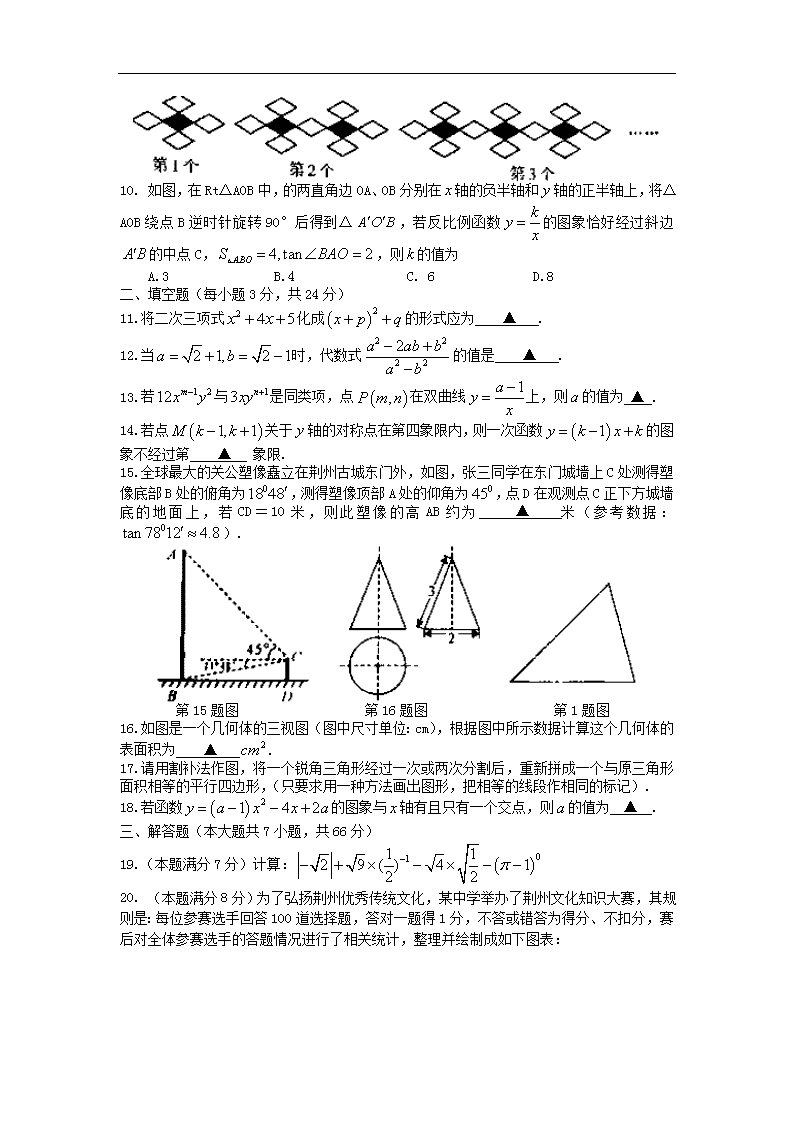
荆州市2016年初中升学考试数学试题 一、选择题（每小题3分，共30分）‎ ‎1. 比0小1的有理数是 A.－1 B.1 C. 0 D.2‎ ‎2.下列运算正确的是 A. B. C. D.‎ ‎3.如图，AB∥CD，射线AE交CD于点F，若∠1＝，则∠2的度数是 A. B. C. D. ‎ ‎ 第3题图 第6题图 第7题图 ‎4.我市气象部门测得某周内七天的日温差数据如下：4，6，6，5，7，6，8（单位：℃），这组数据的平均数和众数分别是 A.7，6 B. 6，5 C. 5，6 D. 6，6‎ ‎5.互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为 A.120元 B.100元 C. 80元 D.60元 ‎6.如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是优弧上不与点A、点C重合的一个动点，连接AD、CD，若∠APB＝80°，则∠ADC的度数是 A.15° B.20° C. 25° D.30°‎ ‎7.如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中∠ABC的余弦值是 A. B. C. D. ‎ ‎8.如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E，若BC＝3，则DE的长为 A.1 B.2 C. 3 D.4‎ ‎ ‎ ‎ 第8题图 第10题图 ‎9.如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n个图案中有2017个白色纸片，则n的值为 A.671 B.672 C. 673 D.674‎ ‎10. 如图，在Rt△AOB中，的两直角边OA、OB分别在轴的负半轴和轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△，若反比例函数的图象恰好经过斜边的中点C，，则的值为 A.3 B.4 C. 6 D.8‎ 二、填空题（每小题3分，共24分）‎ ‎11.将二次三项式化成的形式应为 ▲ .‎ ‎12.当时，代数式的值是 ▲ .‎ ‎13.若与是同类项，点在双曲线上，则的值为 ▲ .‎ ‎14.若点关于轴的对称点在第四象限内，则一次函数的图象不经过第 ▲ 象限.‎ ‎15.全球最大的关公塑像矗立在荆州古城东门外，如图，张三同学在东门城墙上C处测得塑像底部B处的俯角为，测得塑像顶部A处的仰角为，点D在观测点C正下方城墙底的地面上，若CD＝10米，则此塑像的高AB约为 ▲ 米（参考数据：）.‎ ‎ 第15题图 第16题图 第1题图 ‎16.如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据计算这个几何体的表面积为 ▲ .‎ ‎17.请用割补法作图，将一个锐角三角形经过一次或两次分割后，重新拼成一个与原三角形面积相等的平行四边形，（只要求用一种方法画出图形，把相等的线段作相同的标记）.‎ ‎18.若函数的图象与轴有且只有一个交点，则的值为 ▲ .‎ 三、解答题（本大题共7小题，共66分）‎ ‎19.（本题满分7分）计算：‎ ‎20. （本题满分8分）为了弘扬荆州优秀传统文化，某中学举办了荆州文化知识大赛，其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答为得分、不扣分，赛后对全体参赛选手的答题情况进行了相关统计，整理并绘制成如下图表：‎ 组别 分数段 频数（人）‎ 频率 ‎1‎ ‎50≤﹤60‎ ‎30‎ ‎0.1‎ ‎2‎ ‎60≤﹤70‎ ‎45‎ ‎0.15‎ ‎3‎ ‎70≤﹤80‎ ‎60‎ ‎4‎ ‎80≤﹤90‎ ‎0.4‎ ‎5‎ ‎90≤﹤100‎ ‎45‎ ‎0.15‎ 请根据以上图表信息，解答下列问题：‎ ‎（1）表中 ▲ ， ▲ ；‎ ‎（2）补全频数分布直方图；‎ ‎（3）全体参赛选手成绩的中位数落在第几组；‎ ‎（4）若得分在80分以上（含80分）的选手可获奖，记者从所有参赛选手中随机采访1人，求这名选手恰好是获奖者的概率.‎ ‎21.（本题满分8分）如图，将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开，得到△ACD，再将△ACD沿DB方向平移到△的位置，若平移开始后点未到达点B时，交CD于E，交CB于点F，连接EF，当四边形为菱形时，试探究△的形状，并判断△与△是否全等？请说明理由.‎ A ‎22.（本题满分9分）为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用（元）与购买数量（棵）之间存在如图所示的函数关系.‎ ‎（1）求与的函数关系式；‎ ‎（2）若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用.‎ ‎23.（本题满分10分）如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB＝15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H.‎ ‎（1）求证：CD是半圆O的切线；‎ ‎（2）若DH＝，求EF和半径OA的长.‎ ‎24.（本题满分12分）已知在关于的分式方程①和一元二次方程②中，、、均为实数，方程①的根为非负数.‎ ‎（1）求的取值范围；‎ ‎（2）当方程②有两个整数根、，为整数，且时，求方程②的整数根；‎ ‎（3）当方程②有两个实数根、，满足，且为负整数时，试判断≤2是否成立？请说明理由.‎ ‎25.（本题满分12分）阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”.例如，点M（1，3）的特征线有：‎ ‎.‎ 问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在轴和轴上，抛物线经过B、C两点，顶点D在正方形内部.‎ ‎（1）直接写出点D所有的特征线；‎ ‎（2）若点D有一条特征线是，求此抛物线的解析式；‎ ‎（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点的位置，当点在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？‎ ‎ ‎ ‎ 第25题图 第25题备用图 ‎