2008湖北恩施自治州中考数学试题

2008湖北恩施自治州中考数学试题

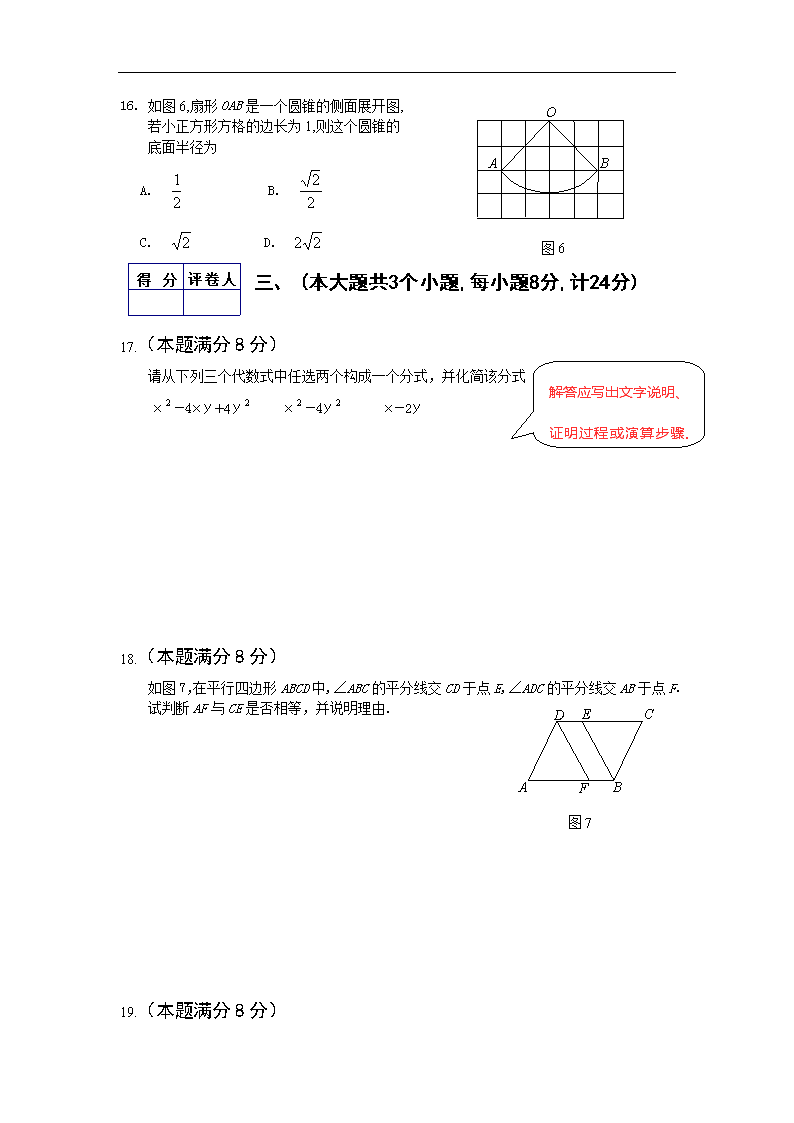
认 真 填一填评卷人得 分 二○○八年恩施自治州初中毕业生学业考试 数 学 试 题 题号 一 二 三 四 五 六 总分 总分人 得分 温馨提示： 亲爱的同学，你好！今天是展示你才能的时候了，只要你仔细审题、认真答题，把平 常的水平发挥出来，就一定会有出色的表现，放松一点，相信自己的实力！ 1．试卷满分 120 分，答卷时间 120 分钟； 2. 允许使用科学计算器. 一、填空题：（请将答案填写在题中的横线上．本大题 共8个小题，每小题3分，计24分） 1. －2的倒数是 . 2. 计算(－a ) = . 3. 2008 年北京奥运会开幕式将于 8 月 8 日在被喻为“鸟巢”（如图 1）的国家体育场举行. 国家体育场建筑面积为 25.8 万㎡,这个数用科学记数法表示为 ㎡. 4. 如图 2，该图形经过折叠可以围成一个正方体形,折好以后,与“静”字相对的字 是 . 5. 如图 3,在 Rｔ△ABC 中,∠ACB=90°，CD⊥AB，D 为垂足.在不添加辅助线的情况下,请写 出图中一对相等的锐角: .(只需写出一对即可) 6. 一家商店将某种服装按成本价提高 40%后标价,又 以 8 折优惠卖出,结果每件仍获利 15 元,这种服装 每件的成本为 元. 7. 已知菱形的两对角线长分别为 6㎝和 8㎝,则菱形 的面积为 ㎝2. 8. 将杨辉三角中的每一个数都换成分数 ，得到一个 如图 4 所示的分数三角形，称莱布尼茨三角形.若 用有序实数对(ｍ，ｎ)表示第ｍ行,从左到右第ｎ 个数,如(4,3)表示分数 .那么(9,2)表示的分数 是 . 3 2 12 1 图 1 考 应静冷着 沉 图 2 6 1 2 1 3 1 2 1 3 1 4 1 12 1 12 1 4 1 1 1 … … 图 4 第 1 行 第 2 行 第 3 行 第 4 行 21 D C BA 图 3 仔 细 选 一选哟！ 评卷人得 分 二、选择题：（下列各小题都给出了四个选项，其中只有一项是 符合题目要求的，请将符合要求的选项前面的字母代号填写在下面的 答题栏内. 本大题共8个小题，每小题3分，计24分） 9. 9 的算术平方根是 A. ±3 B. 3 C. －3 D. 10. 为了让州城居民有更多休闲和娱乐的地方，政府又新建了几处广场，工人师傅在铺设地 面时，准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖，其中不能进 行平面镶嵌的是 A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形 11. 如果ａ＜ｂ＜0,下列不等式中错误的是 A. ab＞0 B. ａ＋ｂ＜0 C. ＜1 D. ａ－ｂ＜0 12. 在 Rt△ABC 中,∠C=90°,若 AC=2BC,则 tanA 的值是 A. B. 2 C. D. 13. 将一张边长为 30㎝的正方形纸片的四角分别剪去一个边长为ｘ㎝的小正方形,然后折叠 成一个无盖的长方体.当ｘ取下面哪个数值时,长方体的体积最大 A. 7 B. 6 C. 5 D. 4 14. 甲、乙、丙、丁四个小朋友在院里玩球，忽听“砰”的一声，球击中了李大爷家的窗户. 李大爷跑出来查看，发现一块窗户玻璃被打裂了.李大爷问:“是谁闯的祸?” 甲说:“是乙不小心闯的祸.” 乙说:“是丙闯的祸.” 丙说:“乙说的不是实话.” 丁说:“反正不是我闯的祸.” 如果这四个小朋友中只有一个人说了实话,请你帮李大爷判断一下,究竟是谁闯的祸 A.甲 B. 乙 C.丙 D.丁 15. 如图 5,一次函数ｙ =ｘ－1 与反比例函数ｙ = 的图 像交于点 A(2,1),B(－1,－2),则使ｙ ＞ｙ 的ｘ的取 值范围是 A. ｘ＞2 B. ｘ＞2 或－1＜ｘ＜0 C. －1＜ｘ＜2 D. ｘ＞2 或ｘ＜－1 题 号 9 10 11 12 13 14 15 16 答 案 3 b a 2 1 5 5 2 5 1 2 x 2 1 2 O B ｙ ｘ A A A 图 5 评卷人得 分 16. 如图 6,扇形 OAB 是一个圆锥的侧面展开图, 若小正方形方格的边长为 1,则这个圆锥的 底面半径为 A. B. C. D. 三、 (本大题共3个小题,每小题8分,计24分) 17.（本题满分 8 分） 请从下列三个代数式中任选两个构成一个分式，并化简该分式 ｘ －4ｘｙ＋4ｙ ｘ －4ｙ ｘ－2ｙ 18.（本题满分 8 分） 如图 7，在平行四边形 ABCD 中,∠ABC 的平分线交 CD 于点 E,∠ADC 的平分线交 AB 于点 F. 试判断 AF 与 CE 是否相等，并说明理由. 19.（本题满分 8 分） 2 1 2 2 2 22 2 2 2 2 BA O 图 6 F ED C BA 图 7 解答应写出文字说明、 证明过程或演算步骤. 请你一定要注意噢！ 评卷人得 分 手牵着手,心连着心.2008年5月12日发生在四川汶川的特大地震灾害,牵动着全中国人 民的心.某校团支部发出为灾区捐款的倡议后,全校师生奉献爱心,踊跃捐款,已知全校 师生共捐款 4万5千元,其中学生捐款数比老师捐款数的2倍少9千元,该校老师和学生各 捐款多少元? 四、( 本大题共2 个小题, 其中第20 题8 分, 第21 题9 分,计17分) 20. （本题满分 8 分） 如图 8,C 为线段 BD 上一动点,分别过点 B、D 作 AB⊥BD,ED⊥BD,连接 AC、EC.已知 AB=5,DE=1,BD=8,设 CD=x. (1)用含 x 的代数式表示 AC＋CE 的长； (2)请问点 C 满足什么条件时,AC＋CE 的值最小? (3)根据(2)中的规律和结论,请构图求出代数式 的最小值. 21.（本题满分 9 分） 国家教育部规定“中小学生每天在校体育活动时间不低于 1 小时”.为此,我州今年初中 9)12(4 22 +−++ xx 后 面 还 有 哦 ， 请 继 续 努 力 E D CB A 图 8 评卷人得 分 毕业生学业考试体育学科分值提高到 40 分,成绩记入考试总分.某中学为了了解学生体 育活动情况,随机调查了 720 名毕业班学生,调查内容是:“每天锻炼是否超过 1 小时及 未超过 1 小时的原因”,所得的数据制成了如图 9 的扇形统计图和频数分布直方图. 根据图示,解答下列问题: (1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼超 过 1 小时”的学生的概率是多少？ (2)“没时间”的人数是多少？并补全频数分布直方图； (3)2008 年恩施州初中毕业生约为 4.3 万人,按此调查,可以估计 2008 年全州初中毕业 生中每天锻炼未超过 1 小时的学生约有多少万人？ (4)请根据以上结论谈谈你的看法. 锻炼未超过1小时人数频数分布直方图 原因 人数 不喜欢 没时间 其它 图 9 五、(本大题共 2 个小题,其中第 22 题 9 分,第 23 题 10 分,计 19 分) 22.（本题满分 9 分） 如图，AB 是⊙O 的直径，BD 是⊙O 的弦，延长 BD 到点 C，使 DC=BD，连结 AC，过点 D 作 DE⊥AC，垂足为 E. （1）求证：AB=AC； （2）求证：DE 为⊙O 的切线； （3）若⊙O 的半径为 5,∠BAC=60°,求 DE 的长. 23.（本题满分 10 分） E O DC B A 图 10 评卷人得 分 为了落实国务院副总理李克强同志到恩施考察时的指示精神,最近，州委州政府又出台 了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已 知这种产品的成本价为 20 元/千克.市场调查发现,该产品每天的销售量ｗ(千克)与销 售价ｘ(元/千克)有如下关系:ｗ=－2ｘ＋80.设这种产品每天的销售利润为ｙ(元). (1)求ｙ与ｘ之间的函数关系式. (2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少? (3)如果物价部门规定这种产品的销售价不得高于 28 元/千克,该农户想要每天获得 150 元的销售利润,销售价应定为多少元? 六、(本大题满分 12 分) 24.如图 11，在同一平面内,将两个全等的等腰直角三角形 ABC 和 AFG 摆放在一起，A 为公 共顶点，∠BAC=∠AGF=90°，它们的斜边长为 2，若∆ABC 固定不动，∆AFG 绕点 A 旋 转，AF、AG 与边 BC 的交点分别为 D、E(点 D 不与点 B 重合,点 E 不与点 C 重合),设 BE=m，CD=n. （1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明. （2）求 m 与 n 的函数关系式，直接写出自变量 n 的取值范围. （3）以∆ABC 的斜边 BC 所在的直线为 x 轴，BC 边上的高所在的直线为 y 轴，建立平面 直角坐标系(如图 12).在边 BC 上找一点 D，使 BD=CE，求出 D 点的坐标，并通过计算 验证 BD2＋CE =DE . （4）在旋转过程中,(3)中的等量关系 BD ＋CE =DE 是否始终成立,若成立,请证明,若不 成立,请说明理由. 恭喜你顺利完成答题，别忘了认真检查！ 二○○八年恩施自治州初中毕业生学业考试数学试题 2 2 2 2 2 G y x 图 12 O F ED CB A G 图 11 F ED CB A 参考答案及评分说明 一、填空题（本大题共 8 个小题，每小题 3 分，计 24 分） 1. － 2. a 3. 2.58×10 4. 着 5. ∠A=∠2 或 ∠1=∠B 6. 125 7. 24 8. 二、选择题(本大题共 8 个小题,每小题 3 分,计 24 分) 题 号 9 10 11 12 13 14 15 16 答 案 B C C A C D B B 三、(本大题共 3 个小题,每小题 8 分,计 24 分) 17. 解: 4 分 = 6 分 = . 8 分 18. 解:AF=CE 2 分 ∵四边形 ABCD 是平行四边形 ∴AD=CB, ∠A=∠C, ∠ADC=∠ABC 4 分 又∵∠ADF= ∠ADC, ∠CBE= ∠ABC ∴∠ADF=∠CBE 6 分 ∴∆ADF≌∆CBE ∴AF=CE 8 分 19. 解:设老师捐款 x 元,学生捐款 y 元.则有 1 分 4 分 解得 7 分 答:该校老师捐款 18000 元,学生捐款 27000 元. 8 分 2 1 6 5 72 1 22 22 4 44 yx yxyx − +− )2)(2( )2( 2 yxyx yx −+ − yx yx 2 2 + − 2 1 2 1    =+ −= 45000 90002 yx xy    = = 27000 18000 y x 四、(本大题共 2 个小题,其中第 20 题 8 分,第 21 题 9 分,计 17 分) 20. 解: (1) 2 分 (2)当 A、C、E 三点共线时,AC+CE 的值最小 4 分 (3)如下图所示,作 BD=12,过点 B 作 AB⊥BD,过点 D 作 ED⊥BD,使 AB=2,ED=3,连结 AE 交 BD 于点 C.AE 的长即为代数式 的最小值. 6 分 过点 A 作 AF∥BD 交 ED 的延长线于点 F,得矩形 ABDF, 则 AB=DF=2,AF=BD=8. 所以 AE= =13 即 的最小值为 13. 8 分 21. 解:(1) ∴选出的恰好是“每天锻炼超过 1 小时”的学生的概率是 . 2 分 (2)720×(1- )-120-20=400(人) ∴“没时间”的人数是 400 人. 4 分 补全频数分布直方图略. 5 分 (3)4.3×(1- )=3.225(万人) ∴2008 年全州初中毕业生每天锻炼未超过 1 小时约有 3.225 万人. 7 分 (4)说明:内容健康,能符合题意即可. 9 分 五、(本大题共 2 个小题,其中第 22 题 9 分,第 23 题 10 分,计 19 分) 22. 解：(1)证明:连接 AD ∵AB 是⊙O 的直径 ∴∠ADB=90° 又 BD=CD 125)8( 22 +++− xx 9)12(4 22 +−++ xx 22 )23(12 ++ 9)12(4 22 +−++ xx 4 1 360 90 = 4 1 4 1 4 1 F E DCB A ∴AD 是 BC 的垂直平分线 ∴AB=AC 3 分 (2)连接 OD ∵点 O、D 分别是 AB、BC 的中点 ∴OD∥AC 又 DE⊥AC ∴OD⊥DE ∴DE 为⊙O 的切线 6 分 (3)由 AB=AC, ∠BAC=60°知∆ABC 是等边三角形 ∵⊙O 的半径为 5 ∴AB=BC=10, CD= BC=5 又∠C=60° ∴DE=CD·sin60°= 9 分 23. 解:⑴ y＝(x－20)∙ w ＝(x－20)(－2x＋80) ＝－2x2＋120x－1600， ∴y 与 x 的函数关系式为：y＝－2x2＋120x－1600． 3 分 ⑵ y＝－2x2＋120x－1600 ＝－2 (x－30) 2＋200， ∴当 x＝30 时，y 有最大值 200． ∴当销售价定为 30 元/千克时,每天可获最大销售利润 200 元. 6 分 ⑶ 当 y＝150 时，可得方程　－2 (x－30 )2 ＋200＝150． 解这个方程，得 x1＝25，x2＝35． 8 分 根据题意，x2＝35 不合题意,应舍去． ∴当销售价定为 25 元/千克时，该农户每天可获得销售利润 150 元． 10 分 六、(本大题满分 12 分) 24. 解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA 1 分 ∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45° ∴∠BAE=∠CDA 又∠B=∠C=45° ∴∆ABE∽∆DCA 3 分 (2)∵∆ABE∽∆DCA ∴ 由依题意可知 CA=BA= ∴ 2 1 2 35 CD BA CA BE = 2 n m 2 2 = ∴m= 5 分 自变量 n 的取值范围为 1

查看更多