2008大连市中考数学考试

2008大连市中考数学考试

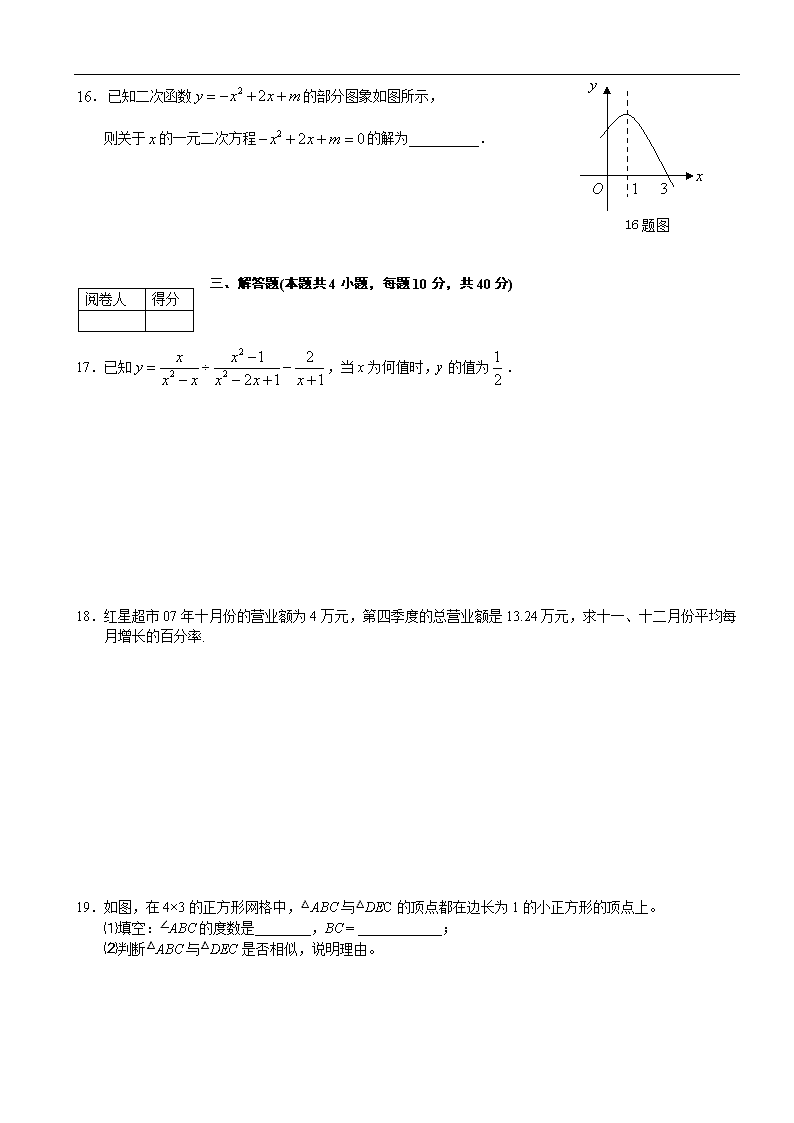
‎2008年大连市䌜毕业升学统一考试旅顺口区试测(一)‎ 数 学 题号 一 二 三 四 五 附加题 总分 分数 本试卷1～8页，共150分，考试时间120分钟。‎ 阅卷人 得分 请考生准备好圆规，直尺、三角板、计算器等答题工具，祝愿所有考生都能发挥最佳水平。‎ ‎ 一、选择题(本题8小题，每小题3分，共24分)‎ ‎ 说明:将下列各题唯一正确的答案代号A、B、C、D填到题后 的括号内。‎ ‎1．如图，小明用手盖住的点的坐标可能为 ( )‎ A．(2，3) B．(2，－3) C．(－2，3) D．(－2，－3)‎ ‎2．下图为各届夏季奥运会的会徽图案，其中是轴对称图形的是（ ）‎ ‎2008年北京 ‎1992年巴塞罗那 ‎1980年莫斯科 ‎1972年慕尼黑 ‎　　　‎ ‎ A． B． C． D．‎ ‎3．下列运算中，正确的是( )‎ A． B． C． D．‎ ‎4．如图所示是某校九年级学生到校方式的条形统计图，‎ 根据图形可得出步行人数占总人数的( )‎ A．60％ B．50％ C．30％ D．20％‎ ‎5．已知⊙O1的半径为5cm，⊙O2的半径为3cm，圆心距O1O2＝2，那么⊙O1与⊙O2的位置关系是（ ）‎ A．相离　 　B．外切　 　C．相交　 　D．内切 ‎6．测得某人的一根头发直径约为0.000 072 85米，用科学记数法表示为( )‎ A．7285×10－8 米 B．7.285×10－5 米 C．0.7285×14－4 米 D．0.7285×10－5米 ‎7．均匀地向一个如图所示的容器中注水，最后把容器注满，在注水过程中水面高度随时间变化的函数图象大致是（ ）.‎ ‎8．下列图形中，一定能够能得出结论的是 （ ）‎ ‎ Ａ． Ｂ． Ｃ． Ｄ． ‎ 阅卷人 得分 ‎ 二、填空题(本题共8小题，每小题3分，共24分)‎ ‎ 说明：将答案直接填在题后的横线上。‎ ‎9．如果某天中午气温是2°C，到了傍晚气温下降了5°C，那么傍晚的气温是__________C°．‎ ‎10．大连电视台2008年5月某日发布的当天的天气预报，我市11个地区当天最高气温（℃）统计如下表：‎ 气温（℃）‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎17‎ 频数 ‎1‎ ‎1‎ ‎1‎ ‎3‎ ‎2‎ ‎2‎ ‎1‎ 那么这些城市当天的最高气温的中位数和众数分别是________，_________．‎ ‎11．不等式组的解集是________________．‎ ‎12．小明的身高是1.7m，他的影长是2m，同一时刻学校旗杆的影长是10m，‎ 则旗杆的高是_________m．‎ ‎13题图 ‎13．如图，P为正方形ABCD内的一点，△ABP绕点B顺时针旋转得到△CBE，‎ 则△BPE是 三角形．‎ ‎15题图 ‎14．矩形的面积为2，一条边长为x，另一条边长为y，则y与x的函数关 系式为(不必写出自变量取值范围)____________________．‎ ‎15．如图，△ABC后的图形是△A′B′C′，其中C与C′是对应点，‎ 请画出平移后的三角形△A′B′C′．‎ ‎16题图 ‎16．已知二次函数的部分图象如图所示，‎ 则关于的一元二次方程的解为 ． ‎ 阅卷人 得分 三、解答题(本题共4小题，每题10分，共40分) ‎ ‎ ‎ ‎17．已知，当x为何值时，y的值为．‎ ‎18．红星超市07年十月份的营业额为4万元，第四季度的总营业额是13.24万元，求十一、十二月份平均每月增长的百分率.‎ ‎19．如图，在4×3的正方形网格中，△ABC与△DEC的顶点都在边长为1的小正方形的顶点上。‎ ‎⑴填空：∠ABC的度数是________，BC = ____________；‎ ‎⑵判断△ABC与△DEC是否相似，说明理由。‎ ‎20．小明和小芳设计了这样一个游戏，规则是：把三个完全一样的小球分别标上数字1、2、3后，放在一个不透明的口袋里，小明先随意摸出一个球，记住球上标注的数字，然后让小芳同学抛掷一个质地均匀的、各面分别标有数字1、2、3、4、5、6的正方体骰子，又得到另一个数字，再把两个数字相加．若两人的数字之和小于7，则小明获胜；否则，小芳获胜．‎ ‎⑴请你用画树状图或列表法把两人所得的数字之和的所有结果都列举出来；‎ ‎⑵这个游戏公平吗？如果公平，请说明理由；如果不公平，请你加以改进，使游戏变得公平．‎ 阅卷人 得分 四、解答题(本题共3小题，其中21题 9分，22、23题各10分，共28分)‎ ‎21．在某张航海图上，标明了三个观测点的坐标为O（0，0），B（12，0），C（12，16），由三个观测点确定的圆形区域是海洋生物保护区，如图所示．‎ ‎⑴求圆形区域的面积（π取3.14）；‎ ‎⑵某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°方向上，同时在观测点B测得A位于北偏东30°方向上，请作图确定A点的位置，并求观测点B到渔船A的距离（结果保留三个有效数字）；‎ ‎⑶请直接判断并写出如果渔船A继续向西航行，能否闯入保护区．‎ ‎22．某街道建起一座天然气供应站,气站根据实际情况,每天从零点开始至凌晨4点,只打开进气阀,在以后的16小时(4∶00—20∶00),同时打开进气阀和供气阀, 20∶00—24∶00只打开供气阀，已知气站每小时进气量和供气量是一定的，下图反映了某天储气量y(米)与x(小时)之间的关系，如图下图所示： ‎ ‎⑴求0∶00—20∶00之间气站每小时增加的储气量；‎ ‎⑵求20∶00—24∶00时，y与x的函数关系式，并画出函数图象；‎ ‎⑶照此规律运行，从这天零点起三昼夜内，经过多少小时气站储气量 达到最大？并求出最大值．‎ ‎23．⑴操作：如图23－1，O是边长为a的正方形ABCD的中心，将一块半径足够长、圆心角为直角的扇形纸板的圆心放在O点处，并将纸板绕O点旋转．‎ ‎ 求证：正方形ABCD的边被纸板覆盖部分的总长度为定值a．‎ ‎ ⑵思考：如图23－2，将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或边长为a的正五边形的中心O点处，并将纸板绕O点旋转．当扇形纸板的圆心角为__________时，正三角形的边被纸板覆盖部分的总长度为定值a；如图23－3，当扇形纸板的圆心角为_________时，正五边形的边被纸板覆盖部分的总长度为定值a.(直接填空)‎ ‎ ⑶探究：一般地，将一块半径足够长的扇形纸板的圆心放在边长为a的正n边形的中心O 点处，并将纸板绕O点旋转，当扇形纸板的圆心角为________度时，正n边形的边被纸板覆盖部分的总长度为定值a；‎ 这时正n边形被纸板覆盖部分的面积是否也为定值？若为定值，写出它与正n边形面积S之间的关系(不需证明)；若不是定值，请说明理由。‎ 阅卷人 得分 ‎ 五、解答题和附加题(本题共3小题，24题 10分，25题14分，26题10分，共34分，‎ 附加题5分，全卷累积不超过150分，建议考生最后答附加题)‎ ‎24．如图24－1，P1、P2、P3、……、Pn分别是抛物线与直线、、、……、 的交点，连结P1P2、P2P3，……，Pk－1Pk．‎ ‎⑴求△OP1P2的面积，并直接写出△OP2P3 的面积；‎ ‎⑵如图24－2，猜想△OPk－1Pk的面积，并说明理由；‎ ‎⑶若将抛物线改为抛物线，其它条件不变，猜想△OPk－1Pk的面积(直接写出答案)．‎ 图24－1‎ ‎．‎ 图24－2‎ ‎25．两个全等的三角形如下图所示放置，点B、A、D在同一直线上．‎ 操作：在图25中，在CB边上截取CM = AB，连结DM，交AC于N．‎ 请探究∠AND的大小，并证明你的结论．‎ ‎26．已知抛物线M：y = -x2+2mx+n（m，n为常数，且m> 0，n>0）的顶点为A，与y轴交于点C；抛物线N与抛物线M关于y轴对称，其顶点为B，连结AC，BC，AB．‎ 问抛物线M上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．‎ 说明：⑴如果你反复探索,没有解决问题, 请写出探索过程(要求至少写3步)；‎ ‎⑵在你完成⑴之后,可以从①、②中选取一个条件，完成解答（选取①得7分；选取②得10分）．‎ ‎①；②．‎ 附加题: 若将26题中“抛物线M：y= -x2+2mx+n（m，n为常数，且m> 0，n>0） ”改为“抛物线M：y= ax2+2mx+n（m，n为常数，且m≠ 0,a≠0, n>0） ”，其他条件不变, 探究 26题中问题．‎ 参考答案：(解答题答案及赋分仅供参考，评分时可根据学生答题情况酌情处理)‎ 一、 选择题 ‎1．B 2．C 3．A 4．B 5．D 6．B 7．A 8．D 二、填空题 ‎9．－3‎ ‎10．13C°，13C°‎ ‎11．‎ ‎12．8.5‎ ‎13．等腰直角 ‎14．‎ ‎15．图略 ‎16．－1和3‎ 三、解答题 ‎17．‎ ‎∴当y的值为时，…………………………7′‎ 解得x = －3………………………………………………；9′‎ 经检验x = －3是这个方程的解，且原式有意义，所以当x = －3时，y的值为…………………10′‎ ‎18．解：设第十一、十二月份平均每月增长的百分率为x，……………………………………1′‎ 由题意得，…………………………………………………………5′‎ 解得x 1= 0.1，x2 = －3.1(舍去)‎ 所以x = 0.1 = 10%……………………………………………………………………9′‎ 答：第十一、十二月份平均每月增长的百分率为10％………………10′‎ ‎19．⑴135°，………………………………………………………2′‎ ‎⑵相似……………………………………………………………………3′‎ ‎∵BC = ，EC = ……………………………………………5′‎ ‎∴，‎ ‎∴……………………………………………………………………………8′‎ 又由∠ABC = ∠CED = 135°……………………………………………………………9′‎ ‎∴△ABC∽△DEC．…………………………………………………………………10′‎ ‎20．⑴画树状图图或列表正确6分；‎ ‎⑵根据树状图或表格说明理由和设计游戏4分．‎ 四、解答题 ‎21．⑴连结BC、OA，则∠OBC = 90°，BC = 16………………1′‎ ‎∴OC是直径，OC = ‎ ‎∴圆的半径为10……………………………………………………2′‎ ‎∴圆的面积为………………………………3′‎ ‎⑵作图正确 …………………………………………………………4′‎ 如图，作AD⊥x轴于D，‎ 在Rt△ABD中，由，得AD = BD…………5′‎ ‎△AOD是等腰直角三角形，得OD = AD =BD……………………6′‎ 所以BD－BD = 12，得BD = ………………………7′‎ 所以AB = 2BD = 12≈32.8………………………………8′‎ ‎22．.解:⑴由图象可知：在0∶00— 4∶00之间气站储气量从30米增加到230米 那么0∶00—4∶00之间气站每小时增加的储气量为(米)……………………1′‎ 同理可求4∶00—20∶00之间气站每小时增加的储气量为 (米)……………2′‎ ‎ ⑵由⑴可知：气站每小时供气量为 (米)…………………………………………3′‎ ‎∴24时储气量为 (米)………………………………………………………4′‎ ‎∴点(20,238)和点(24,40)满足与的函数关系式，设所求函数关系式为： ‎ 则有： 解得：………………6′‎ ‎∴与的函数关系式为： (20≤≤24) ‎ 图象如图所示……………………………………………………8′ ‎ ‎⑶ 由⑵可知：24时气站储气量是40米，‎ ‎∴每天储气量增加40－30 = 10 (米)‎ 由图象可知每天20∶00时气站储气量达到最大值，‎ 所以三昼夜内，第三天的20∶00时，即经过了小时，‎ 气站的储气量达到最大；…………………………………………………………………………9′‎ 最大值为(米)………………………………………………………………10′‎ ‎23．⑴在正方形ABCD中，设扇形两半径交AB、AD分别于E、F 作连结OA、OD．…………………………………………………1′‎ ‎∵O是正方形ABCD的中心，‎ ‎∴OA = OD，∠OAD =∠ODA = 45°，‎ ‎∴∠AOD = 90°…………………………………………………2′‎ ‎∵扇形的圆心角∠EOF = 90°‎ ‎∴∠AOE＋∠AOF = ∠DOF + ∠AOF ‎∴∠AOE =∠DOF………………………………………………3′‎ ‎∴△AOE≌△DOF(ASA)………………………………………5′‎ ‎∴AE = DF………………………………………………………6′‎ 所以被纸板覆盖部分的总长度为AF + EF = AF + DF = AD = a为定值．…………………………7′‎ ‎⑵120°，72°……………………………………………………9′‎ ‎⑶……………………………………………………………10′‎ 是定值，被纸板覆盖部分的面积是．………………………12′‎ 五、解答题 ‎24．⑴∵P1是抛物线与直线交点，‎ 由，解得x1 = 1，x2 = 0(舍去)‎ 代入，，解得y = 1‎ 所以P1点坐标为(1，1)…………………………1′‎ 同理，可求出P2点坐标为(2，4)………………2′‎ 过P2作x轴的垂线交直线y = x于M，‎ 过P1作P2Q⊥P2M于N ‎∵M在直线y = x上，‎ ‎∴M点坐标为(2，2)，…………………………3′‎ ‎∴P2M = 4－2 = 2‎ PN = 2－1 = 1……………………………………4′‎ ‎∴…………5′．‎ ‎△OP2P3的面积是3………………………………………6′．‎ ‎⑵△OPk－1Pk的面积是………………………7′‎ 方法同⑴， 求得Pk点坐标为(，)，Pk－1坐标为(，)，M坐标为(k，)‎ PKM = ‎ ‎……………………10′‎ ‎⑶△OPk－1Pk的面积是………………………………12′‎ ‎25．作图基本正确，确定M，连结DM，确定交点N……………………1′‎ ‎ 猜测∠AND = 45°………………………………………………………2′‎ 证明：∵Rt△ABC≌Rt△DEA ‎∴AE =AC，∠EAD =∠ACB，AB = DE……………………………3′‎ 延长ED至点F，使DE=DF，连结AF、CF，‎ ‎∵EF⊥AD ‎∴AF=AE，∴∠FAD=∠EAD ‎∴AF=AC，∠FAD =∠ACB…………………………5′‎ ‎∵在Rt△ABC中，∠B=90°，‎ ‎∴∠BAC＋∠ACB＝90°‎ ‎∴∠BAC＋∠FAD＝90°‎ ‎∴∠FAC＝90°………………………………………7′‎ ‎∴△FAC是等腰直角三角形，‎ ‎∴∠ACF＝45°………………………………………8′‎ ‎∵BC⊥AD，EF⊥A D ‎∴BC∥EF………………………………………………9′‎ ‎∵CM = AB = DE = DF = DF ‎∴四边形FDMC为平行四边形……………………10′‎ ‎∴CF∥DM………………………………………………11′‎ ‎∴∠AND＝∠ACF＝45°……………………………12′‎ ‎26．解：假设抛物线M上存在点P，使得四边形ABCP为菱形，连结CP，作AD⊥x轴于D，交CP于E，‎ 则AD为抛物线M的对称轴，且PC = AB = BC…………………………………………………1′‎ 由抛物线的对称性可得AC=BC， ∴AC = BC = AC．‎ 从而△ABC为等边三角形………………………………………2′‎ P ‎∴∠ACG =∠BCG =30°…………………………………………3′‎ ‎∵四边形ABCP为菱形，且点P在抛物线M上，‎ ‎∴点P与点C关于AD对称 ‎∴∠ACE=90°－ 30° = 60°……………………………………………4′‎ ‎∵由抛物线M配方得，‎ ‎ ……………………5′‎ 点A、C的坐标分别为A(m, m2 +n)、C(0, n)，…………………6′‎ ‎∴AE= m2+n－n= m2, CE = m．…………………………………7′‎ 在Rt△ACE中，…………………8′‎ ‎∴ ∵m> 0 ‎ ‎∴……………………………………………………9′‎ ‎∴抛物线M上存在点P，使得四边形ABCP为菱形，此时……………………10′‎ 附加题: 与⑴类似 点A、C的坐标分别为A(,)、C(0, n)，‎ ‎∴AE= = , CE =‎ a> 0， AE =，CE =，．‎ a<0 AE =， CE =，．‎ ‎∴，．…………………………………………………………5′‎