中考复习矩形菱形正方形含答案

中考复习矩形菱形正方形含答案

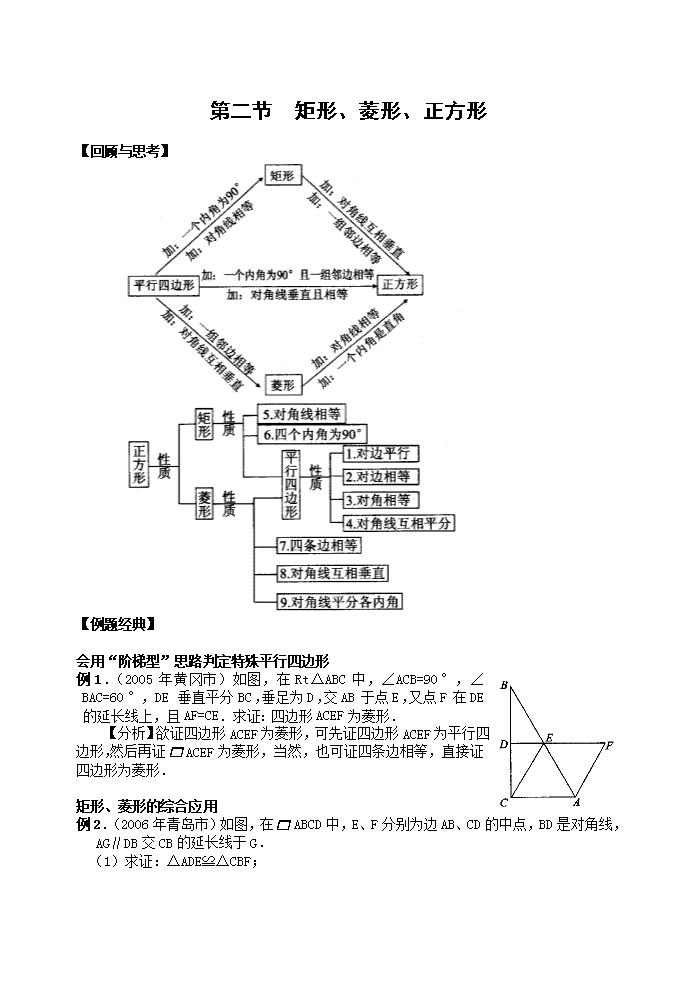
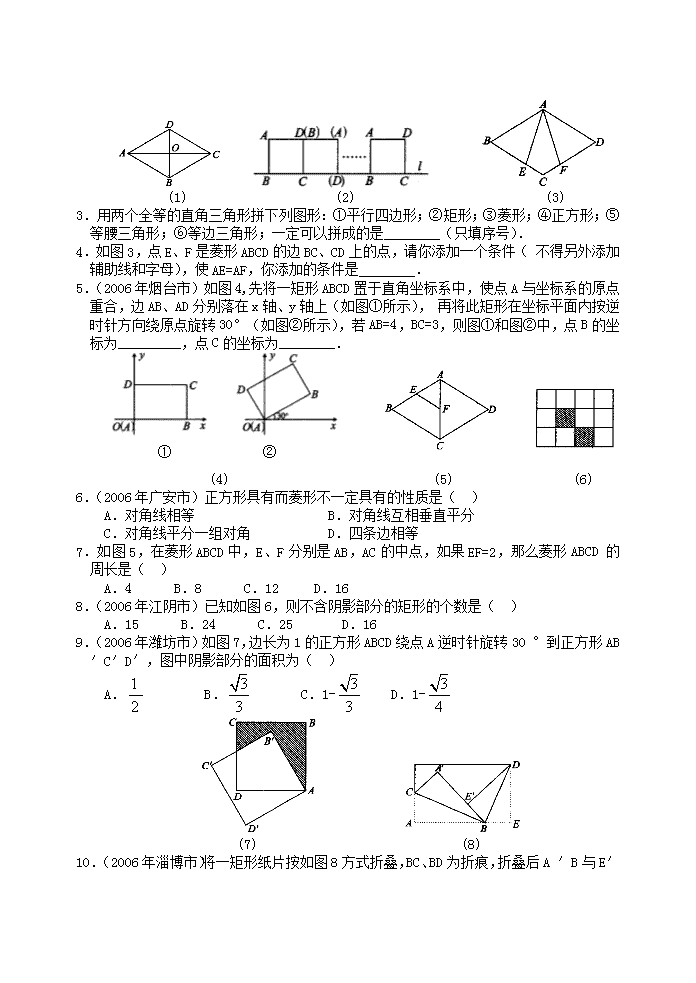
第二节 矩形、菱形、正方形 ‎【回顾与思考】‎ ‎【例题经典】‎ 会用“阶梯型”思路判定特殊平行四边形 例1．（2005年黄冈市）如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°，DE垂直平分BC，垂足为D，交AB于点E，又点F在DE的延长线上，且AF=CE．求证：四边形ACEF为菱形．‎ ‎ 【分析】欲证四边形ACEF为菱形，可先证四边形ACEF为平行四边形，然后再证ACEF为菱形，当然，也可证四条边相等，直接证四边形为菱形．‎ 矩形、菱形的综合应用 例2．（2006年青岛市）如图，在ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．‎ ‎（1）求证：△ADE≌△CBF；‎ ‎（2）若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．‎ ‎ 【解析】（1）∵四边形ABCD是平行四边形 ‎ ∴∠1=∠C，AD=CB，AB=CD．‎ ‎ ∵点E、F分别是AB、CD的中点，‎ ‎ ∴AE=AB，CF=CD．‎ ‎ ∴AE=CF．‎ ‎ ∴△ADE≌△CBF．‎ ‎ （2）当四边形BEDF是菱形时，四边形AGBD是矩形．‎ ‎ ∵四边形ABCD是平行四边形，‎ ‎ ∴AD∥BC．‎ ‎ ∵AG∥BD，‎ ‎ ∴四边形AGBD是平行四边形．‎ ‎ ∵四边形BEDF是菱形，‎ ‎ ∴DE=BE．‎ ‎ ∵AE=BE，‎ ‎ ∴AE=BE=DE．‎ ‎ ∴∠1=∠2，∠3=∠4．‎ ‎ ∵∠1+∠2+∠3+∠4=180°，‎ ‎ ∴2∠2+2∠3=180°．‎ ‎ ∴∠2+∠3=90°．‎ ‎ 即∠ADB=90°，‎ ‎ ∴四边形AGBD是矩形．‎ 会解决与特殊平行四边形有关的动手操作问题 例3．（2005年吉林省）如图，在矩形纸片ABCD中，AB=3，BC=6，沿EF折叠后，点C落在AB边上的点P处，点D落在点Q处，AD与PQ相交于点H，∠BPE=30°．‎ ‎ （1）求BE、QF的长．（2）求四边形PEFH的面积．‎ ‎ 【分析】折叠型试题是近年中考试题的热点，要想解好此类题，考生必须有想像力，抓住折叠的角与边不发生变化，必要时需要考生剪一个四边形实际折叠一下帮助理解．‎ ‎【考点精练】‎ 一、基础训练 ‎1．如图1，在菱形ABCD中，已知AB=10，AC=16，那么菱形ABCD的面积为________．‎ ‎2．（2006年黄冈市）如图2,将边长为‎8cm的正方形ABCD的四边沿直线L向右滚动（不滑动），当正方形滚动两周时，正方形的顶点A所经过的路线的长是________cm．‎ ‎ ‎ ‎ (1) (2) (3)‎ ‎3．用两个全等的直角三角形拼下列图形：①平行四边形；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形；一定可以拼成的是________（只填序号）．‎ ‎4．如图3，点E、F是菱形ABCD的边BC、CD上的点，请你添加一个条件（不得另外添加辅助线和字母），使AE=AF，你添加的条件是________．‎ ‎5．（2006年烟台市）如图4,先将一矩形ABCD置于直角坐标系中，使点A与坐标系的原点重合，边AB、AD分别落在x轴、y轴上（如图①所示），再将此矩形在坐标平面内按逆时针方向绕原点旋转30°（如图②所示），若AB=4，BC=3，则图①和图②中，点B的坐标为_________，点C的坐标为________．‎ ‎① ②‎ ‎ ‎ ‎ (4) ‎ ‎ (4) (5) (6)‎ ‎6．（2006年广安市）正方形具有而菱形不一定具有的性质是（ ）‎ ‎ A．对角线相等 　　　　B．对角线互相垂直平分 ‎ C．对角线平分一组对角 　　　　D．四条边相等 ‎7．如图5，在菱形ABCD中，E、F分别是AB，AC的中点，如果EF=2，那么菱形ABCD的周长是（ ）‎ ‎ A．4 B．‎8 C．12 D．16‎ ‎8．（2006年江阴市）已知如图6，则不含阴影部分的矩形的个数是（ ）‎ ‎ A．15 B．‎24 C．25 D．16‎ ‎9．（2006年潍坊市）如图7，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，图中阴影部分的面积为（ ）‎ A． B． C．1- D．1-‎ ‎ ‎ ‎ (7) (8)‎ ‎10．（2006年淄博市）将一矩形纸片按如图8方式折叠，BC、BD为折痕，折叠后A′‎ B与E′B在同一条直线上，则∠CBD的度数（ ）‎ ‎ A．大于90° B．等于90° C．小于90° D．不能确定 二、能力提升 ‎11．如图，矩形ABCD中，M是AD的中点．‎ ‎ （1）求证：△ABM≌△DCM；‎ ‎（2）请你探索，当矩形ABCD的一组邻边满足何种数量关系时，有BM⊥CM成立，说明你的理由．‎ ‎12．（2006年泉州市）如图，在矩形ABCD中，E、F分别是BC、AD上的点，且BE=DF．‎ 求证：△ABE≌△CDF．‎ ‎13．（2006年沪州市）如图，在矩形ABCD中，点E是BC上一点，AE=AD，DF⊥AE，垂足为F．线段DF与图中哪一条线段相等？先将你的猜想出的结论填写在下面的横线上，然后再加以证明．‎ 即DF=________．（写出一线段即可）‎ ‎14．已知：如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于E、F，求证：四边形AFCE是菱形．‎ 三、应用与探究 ‎15．（2006年河南省）如图，在△ABC中，∠ACB=90°，AC=2，BC=3．D是BC边上一点，直线DE⊥BC于D，交AB于E，CF∥AB交直线DF于F．设CD=x．‎ ‎ （1）当x取何值时，四边形EACF是菱形？请说明理由；‎ ‎ （2）当x取何值时，四边形EACD的面积等于2？‎ 答案：‎ 例题经典 ‎ 例3．（1）BE=2，QF=1 （2）7‎ 考点精练 ‎ ‎1．96 2．16+16 3．①②⑤ ‎ ‎4．∠BAE=∠DAF（答案不唯一） ‎ ‎5．B（4，0），（2，2），C（4，3），（） ‎ ‎6．A 7．D 8．C 9．C 10．B ‎ ‎11．（1）略 （2）AB=AD时，BM⊥CM ‎ ‎12．根据SAS证△ABE≌△CDF ‎ ‎13．DF=DC．证略 ‎ ‎14．证△AOE≌△COF．即得AEFC．四边形AFCE是平行四边形．‎ 又AC⊥EF，∴四边形AFCE是菱形 ‎ ‎15．解：（1）∵∠ACB=90°，‎ ‎∴AC⊥BC．又∵DE⊥BC，∴EF∥AC．‎ 又∵AE∥CF，∴四边形EACF是平行四边形．‎ 当CF=AC时，四边形ACFE是菱形．‎ 此时，CF=AC=2，BD=3-x，tan∠B=，ED=BD·tan∠B=（3-x），‎ ‎∴DF=EF-ED=2-（3-x）=x．‎ 在Rt△CDF中，CD2+DF2=CF2，‎ ‎∴x2+（x）2=22，∴x=±（负值不合题意，舍去），‎ 即当x=时，四边形ACFE是菱形 ‎ ‎（2）由已知得，四边形EACD是直角梯形，S梯形EACD=×（4-x）·x=-x2+2x．‎ 依题意，得-x2+2x=2，整理得，x2-6x+6=0．解之，得x1=3-，x2=3+．‎ ‎∵x=3+>BC=3，‎ ‎∴x=3+舍去，‎ ‎∴当x=3-时，梯形EACD的面积等于2．‎