深圳实验中学中考数学复习指导
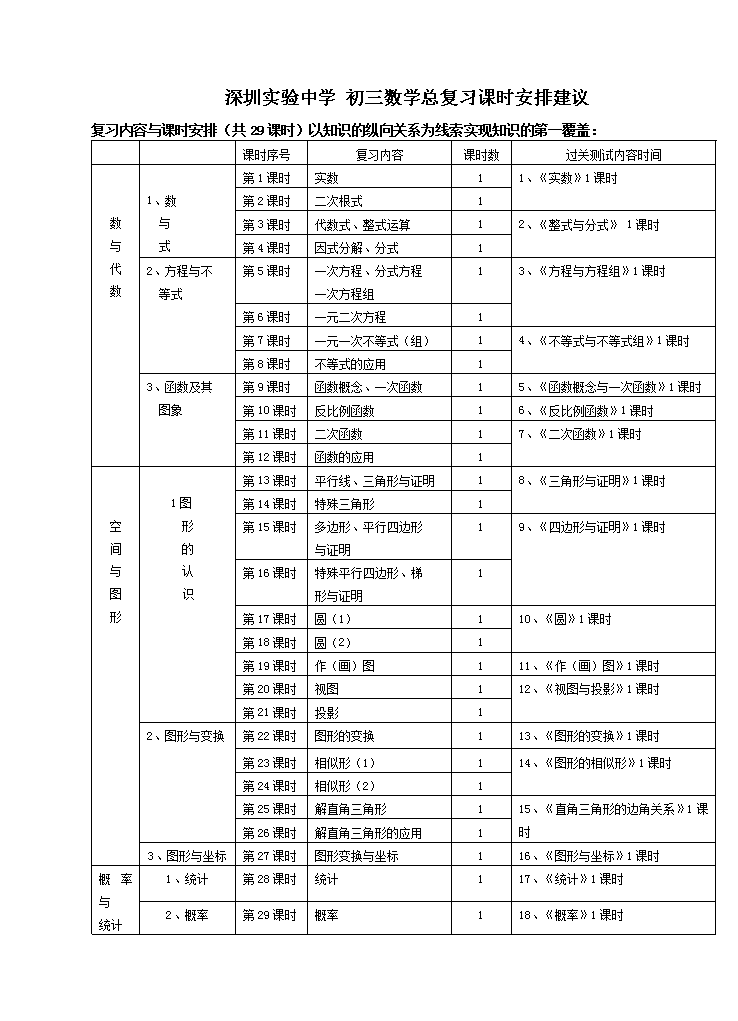
深圳实验中学 初三数学总复习课时安排建议
复习内容与课时安排(共 29 课时)以知识的纵向关系为线索实现知识的第一覆盖:
课时序号 复习内容 课时数 过关测试内容时间
数
与
代
数
1、数
与
式
第 1 课时 实数 1 1、《实数》1 课时
第 2 课时 二次根式 1
第 3 课时 代数式、整式运算 1 2、《整式与分式》 1 课时
第 4 课时 因式分解、分式 1
2、方程与不
等式
第 5 课时 一次方程、分式方程
一次方程组
1 3、《方程与方程组》1 课时
第 6 课时 一元二次方程 1
第 7 课时 一元一次不等式(组) 1 4、《不等式与不等式组》1 课时
第 8 课时 不等式的应用 1
3、函数及其
图象
第 9 课时 函数概念、一次函数 1 5、《函数概念与一次函数》1 课时
第 10 课时 反比例函数 1 6、《反比例函数》1 课时
第 11 课时 二次函数 1 7、《二次函数》1 课时
第 12 课时 函数的应用 1
空
间
与
图
形
1 图
形
的
认
识
第 13 课时 平行线、三角形与证明 1 8、《三角形与证明》1 课时
第 14 课时 特殊三角形 1
第 15 课时 多边形、平行四边形
与证明
1 9、《四边形与证明》1 课时
第 16 课时 特殊平行四边形、梯
形与证明
1
第 17 课时 圆(1) 1 10、《圆》1 课时
第 18 课时 圆(2) 1
第 19 课时 作(画)图 1 11、《作(画)图》1 课时
第 20 课时 视图 1 12、《视图与投影》1 课时
第 21 课时 投影 1
2、图形与变换 第 22 课时 图形的变换 1 13、《图形的变换》1 课时
第 23 课时 相似形(1) 1 14、《图形的相似形》1 课时
第 24 课时 相似形(2) 1
第 25 课时 解直角三角形 1 15、《直角三角形的边角关系》1 课
时第 26 课时 解直角三角形的应用 1
3、图形与坐标 第 27 课时 图形变换与坐标 1 16、《图形与坐标》1 课时
概 率
与
统计
1、统计 第 28 课时 统计 1 17、《统计》1 课时
2、概率 第 29 课时 概率 1 18、《概率》1 课时
第 1 课 实数
姜龙海
复习教学目标:
1、理解现实世界中具有相反意义的量的含义,会借助数轴理解实数的相反数和绝对值的意
义,会求实数的相反数和绝对值,并会比较实数的大小。
2、了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根和立方根。
3、了解无理数与实数的概念,知道实数与数轴上的点的一一对应的关系,会用一个有理数
估计一个无理数的大致范围,了解近似数与有效数字的概念,会用计算器进行近似计算。
4、结合具体问题渗透化归思想,分类讨论的数学思想方法。
复习教学过程设计:
Ⅰ [唤醒]
一、填空:
1、-1.5 的相反数是 、倒数是 、绝对值是 、1- 2 的绝对值是 。
2、倒数等于本身的数是 ,绝对值等于本身的数是 。算术平方根等于本身
的数是 ,立方根等于本身的数是 。
3、2-1= ,-2-2= ,(-1
2 )-2= ,(3.14-∏ )0=
4、在22
7 ,∏,- 8 ,3 (-64) ,sin600,tan450 中,无理数共有 个。
5、用科学记数法表示:-3700000= ,0.000312=
用科学记数法表示的数 3.4×105 中有 个有效数字,它精确到 位。
6、点 A 在数轴上表示实数 2,在数轴上到 A 点的距离是 3 的点表示的数是 。
7、3 260 精确到 0.1 的近似值为 ,误差小于 1 的近似值为 。
8、比较下列各位数的大小:-2
3 -3
4 ,0 -1, tan300 sin600
二、判断:
1、不带根号的数都是有理数。( ) 2、无理数都是无限小数。( )
3、
2 3
2
是分数,也是有理数。( )4、3-2 没有平方根。( )
5、若3 x =x ,则 x 的值是 0 和 1。( )6、a2 的算术平方根是 a。( )
三、选择:
1、和数轴上的点一一对应的数是( )
A、整数 B、有理数 C、无理数 D、实数
2、已知:xy< 0,且|x|=3 ,|y|=1,则 x+y 的值等于( )
A、2 或-2 B、4 或-4 C、4 或 2 D、4 或-4 或 2 或-2
3、如果一个数的平方根与立方根相同,这个数为( )
A、0 B、1 C、0 或 1 D、0 或+1 或-1
Ⅱ[尝试]
例 1 , 已 知 下 列 各 数 : ∏ , -2.6 ,
22
7 ,0,0.4,-(-3),3 (-27) ,(-1
2 )-2,cos300,2 3.6 ,-10,0.21221222122221……(按此规律,从左至右,
在每相邻的两个 1 之间,每段在原有 2 的基础上再增加一个 2)。把以上各数分别填入相应
的集合。
无理数集合:( …) 有理数集合:( …)整数结集合:
( …)
分数集合:( …) 正数集合:( …)
(解略)提炼:实数的分类思想方法。
例 2,计算下列各题:
1、 20-(-1
2 )2+2-2-3 (-64) 2、(3
8 - 7
24 +11
18 -5
9 )×(-72) 3、(1
2 )-2-23×0.125- 4 +|-1|
2、 解略(答案:1:5;2:-11;3:2
例 3,已知实数 a、b 在数轴上的位置如图所示:
(1)你会比较实数 a、b 的大小吗?
(2)你会比较|a|与|b|的大小吗?相信你能!
(3)在什么条件下b
a
>0? b
a
<0? b
a =0?并说明此时坐标原点的大致位置。
解:(1)a<b,这是因为在数轴上表示的两个数,右边的总比左边的大。
分析:解决问题的关键是数轴的原点的位置,你想按怎样的顺序去变化呢?(可自左向右,
也可自右向左)
(2)当原点在点 a 的左边时,|a|<|b| 当原点在点 a,b 的中点偏左时,|a|<|b|
当原点在点 a,b 的中点时,|a|=|b| 当原点在点 a,b 的中点偏右时,|a|>|b|
当原点在点 b 的右边时,|a|>|b|
(3)当 a,b 同号时(且 a≠0,b≠0),b
a
>0 此时坐标原点在 a 的左侧或 b 的右侧
当 a,b 异号时(且 a≠0,b≠0)b
a
<0 此时坐标原点在 a,b 两点之间
当 a≠0,b=0 时,b
a =0,此时坐标原点在 b 点
提炼:运用绝对值的意义,解决数形结合问题中的动点问题,渗透化归和分类讨论的
数学思想方法,训练学生逆向思维。
Ⅲ[小结]
整数
有理数
1、实数的分类
分数
无理数
什么叫无理数
a b
相反数:
2、实数 a 的 绝对值:
倒数: (当 时)
3、实数的运算和科学记数法
4、运用绝对值的意义,解决数形结合问题中的动点问题,渗透化归和分类讨论的数学思想
方法,注意逆向思维的运用。
Ⅳ[实践]
1、 教师自行设计作业
复习指导用书 P3-4 1,2,3○1 -○3 ○6 ,6 P17 1○1 -○5
第 2 课 二次根式
戴国琴
复习教学目标:
1、 知道平方根,算术平方根,立方根的含义,能说出二次根式的两条运算法则。
2、 会用根号表示并会求数的平方根,算术平方根,立方根,会进行简单的二次根式的四则
运算,会对简单的二次根式进行化简,能估算一个无理数的大致范围并能比较大小。
3、 在解题过程中体会数形结合思想,由特殊到一般的数学思想,并能用它们解决问题。
复习教学过程设计
Ⅰ【唤醒】
一、填空:
定义:平方根,算术平方根,立方根
a · b= ab (a≥0,b≥0) 化简
知识结构(阅读): 运算法则
a
b
= a
b
(a≥0,b>0) 四则运算
1.4 的平方根是 , 64 的算术平方根是 , 立方根是
2.化简: 50 = , 3
8
= , ( 5 )2= , 18 × 8 =
3.比较大小: 15 3.85, -2 7 -3 3 , 3 7-4
8
1
2
4.估算: 44 = (误差小于 0. 1),
3
90 = (误差小于 1)
5.根式 1
2-1
分母有理化的结果是
二、判断:
1.1
9
的平方根是1
3
( ) 2.任何数都有算术平方根 ( )
3.任何数都有立方根 ( ) 4. -4 × -3 = 12 =2 3 ( )
5. 4 9
16
= 4 × 9
16
=2 × 3
4
= 3
2
( ) 6. 5 3 +2 2 =7 5 ( )
三、选择题:
1.下列说法中正确的是 ( )
A、1 没有算术平方根 B、1 的平方根是 1
C、0 的平方根是 0 D、-1 的平方根是-1
2.下列各式中正确的是 ( )
A 、 25 =+ 5 B、 (-3)2 =-3 C、 + 36 = +6 D、 -100 =-10
3.下列语句正确的个数为 ( )
(1)+4 是 64 的立方根,(2)
3
x3 = x,(3) 64 的立方根是 4,,(4)
3
(+8)2 = +4
A、 1 个 B、 2 个 C、 3 个 D、4 个
4.化简 (x-1)2 (x<1)正确的是 ( )
A、 x-1 B、(x-1) 2 C、 1-x D、 无法确定
Ⅱ【尝试】 :
例 1、 计算:(1) 1
5
- 20 + 5
4
- 9
80
(2) 24- 30
2
- 3 × (3- 5 )
(3) (3 2 - 2 6) (5 6 +4 2 ) – ( 3 –1)2
解 (略) (答案:- 29
20
5 , - 3 , 16 3 - 40 )
提炼:(1)对于带根号的无理数的运算,可运用公式 a · b = ab (a≥0,b≥0),
a
b
= a
b
(a≥0,b>0)且这两个公式可以顺向和逆向两个方面运用。
(2)适当运用乘法公式可使运算简化。
(3)计算结果必须简化。
例 2 、 是否存在这样的数,它的平方为 35?如果不存在,请说明理由,如果存在,请写出
来并用作图的方法在数轴上找出表示这个数的实数点。
分析:首先求出符合条件的数+ 35 ,再在数轴上作一个直角三角形,找到表示+ 35 的线段
即可
解 (略)
提炼:(1)在数轴上作这样的点时,常常通过作直角三角形来解决。
(2)本题有两解,防止漏解现象,解题时,应仔细审题,全面考虑,注意数形结合
的思想。
例 3、(1)判断下列各式是否成立,你认为成立的请在括号内打“√”,不成立的打“×”
2+2
3
=2 2
3
( ) 3+3
8
=3 3
8
( )
4+ 4
15
=4 4
15
( ) 5+ 5
24
=5 5
24
( )
(2)判断完以上各题后,你发现了什么规律?请用含有 n 的式子将规律表示出来,并
注明 n 的取值范围。
(3)请用数学知识说明你所写式子的正确性。
分析:先按运算公式计算化简后,再判断找规律。
解:(1)均正确。
(2) n+ n
n 2-1
= n n
n 2-1
( n 为大于 1 的自然数)
(3) n+ n
n 2-1
= n3
n2-1
= n 2 n
n2-1
= n n
n2-1
提炼:本题是一道探索题,由特殊进行观察,归纳,建立猜想,用符号表示并给出证明,体
现了数学中常用的由特殊到一般的思想方法。
Ⅲ【小结】: 1、知识结构见上表
2、基本数学方法:数形结合思想,特殊到一般思想,分类思想等
3、解题注意点:(1)解题时应弄清基本概念,法则
(2) 注意解题的严密性,充分考虑各种情况,防止漏解现象。
Ⅳ【实践】: 1、教师自行设计
2、复习指导用书 p3 练习一 3 、(4) (5) p17 复习题 3 、4。
第 3 课 代数式 整式运算
彭淑霞
复习教学目标:
1. 了解字母表示数的意义,了解单项式、多项式、整式以及单项式的系数与次数、多
项式的项与次数、同类项的概念,并能说出单项式的系数和次数、多项式的项和次
数。知道正整数幂的运算性质,能说出去括号、添括号法则,了解两个乘法公式的
几何背景。
2. 会用代数式表示简单问题中的数量关系,会求代数式的值,会把一个多项式按某个
字母升(降)幂排列,会判断同类项,并能熟练地合并同类项,会准确地进行去括
号与添括号,会推导乘法公式,能运用整式的运算性质、公式以及混合运算顺序进
行简单的整式的加、减、乘、除运算。
3. 通过运用幂的运算性质、整式的运算法则和公式进一步发展观察、归纳、类比、概
括等能力,
会运用类比思想,一般到特殊、再由特殊到一般的数学思想和数形结合思想解决问
题。
复习教学过程设计:
Ⅰ.【唤醒】
知识结构(阅读):
现实世界、其他学科、数学中的问题情境
整式的加减
同底数幂的乘法、幂的乘方、积的乘方
幂
同底数幂的除法、零指数和负整数指数幂
单项式乘单项式
整式的乘法 单项式乘多项式
多项式乘多项式、平方差公式、完全平方公式
单项式除以单项式
整式的除法
多项式除以单项式
一、填空:
1.___ __ 和 _____ __ 统称为整式。
2.
_____( _____(
( ) _____( ( ) _____(
n n
n m
a a m n a a m n
a m n ab m
m m
m
、 都是正整数) 、 都是正整数,且m>n)
、 都是正整数) 是正整数)
0 ____( 0)a a , ____( 0,pa a p 是正整数) ( ) ______m a b c ,
( )( ) __________m n a b
( ) _________am bm cm m ( )( ) __________a b a b
2( ) _________a b 2( ) _________a b
3.整式的混合运算顺序:先________、后________、再________、有括号先____________.
二、判断:
1. 2 213
4
a b ab和 是同类项 。 ( ) 2.
24 4 , 3
3 3
x y 单项式 的系数是 次数是 。( )
3 . 35 2 3x xy 多项式 的次数是五次三项式 。 ( ) 4. 3 3a b c a b c
( )
5 . 2 2 3 3 3 3 2 22 4 5 5 2 4x y xy x y x x y x y xy 多项式 按 的降幂排列为 。
( )
三、选择:
1.某商场实行 7.5 折优惠销售,现售价为 y 元的商品的原价为 ( )
A. 75 y 元 B. (1 75 y 元 C .
75
y
元 D.
1 75
y
元
2 . 4 1 2 31 3 ,
2
m na b a b m n 若 与 是同类项 则 和 的值为
( )
A. 4 和 3 B. 2 和 3 C . 4 和 2 D. 无法确定
3 . 下 列 各 式 计 算 过 程 正 确 的 是
解决问题
整式及其运算
( )
A. 3 2 3 2 5x x x x B. 3 2 3 2 6x x x x C. 6 2 6 2 3x x x x D.
32 2 3 5x x x x
4 . 下 列 各 式 中 , 不 能 用 平 方 差 公 式 计 算 的 是
( )
A. 3 2 2 3a b b a B. 2 24 3 4 3a bc a bc C. 2 3 2 3a b b a D.
3 5 5 3m m
5. 2 216 ,x kxy y k 是完全平方式 则 的值为
( )
A. 4 B. 8 C. 4 或-4 D. 8 或-8
Ⅱ. 【尝试】
例 1.先化简,再求值: 2 22 3 , 2, 1x x y x y x y 其中 。 (答案:11)
例 2.计算: 32 2 7 422 3
3
a b ab a b
分析:按整式混合运算的顺序:先乘方,同级运算从左往右依次进行。(答案:36b)
提炼:在熟练掌握整式的运算法则和幂的运算性质基础上必须严格按照混合运算顺序逐步运
算。
例 3.计算:(1) 222 3 2 3 4 2 3 5x y x y x y x y ;(2) 4 3 2 4 3 2a b c a b c
分析:第(1)题根据混合运算法则先合理使用乘法公式,后进行整式的加减运算。
第(2)题先将原式转化为 4 3 2 4 3 2a b c a b c 的形式,后运用平方差公式
将其化为 2216 3 2a b c 的形式,最后利用完全平方公式计算即可。(答案见复习指
导用书第 11 页)
提炼:根据乘法公式的特点将原题中的代数式变形为符合公式特点的形式是解此类题的关
键。
例 4. 见《复习指导用书》第 6 页例 2
分析:解决本题时学生往往着眼于分析表格中的数据的变化,应指导学生结合具体的图形观
察图形的形成规律,着重在摆成的平行四边形的两组对边与菱形和等腰梯形的边长之
间的关系。
提炼:本例是一道探索题,首先给出了几个特殊的图形,然后根据这些特殊的图形的周长,
进行探索、归纳、猜想,得到一般图形的周长,体现了数学中常见的由一般到特殊、
再由一般到特殊的思想方法以及数形结合思想。
Ⅲ. 【小结】
1. 本单元的知识结构(见填空)。
2. 本节课运用的数学思想方法:类比思想,一般到特殊、再由特殊到一般的思想方法和数形结
合思想等。
Ⅳ. 【实践】
1. 教师自行设计作业。
2. 复习指导用书第 9 页第 3、7、8 题和第 12 页第 3 题。
第 4 课时 因式分解 分式
王爱军
复习教学目标
1、 知道因式分解、分式的概念;能说出分式的基本性质。
2、 会灵活应用四种方法进行因式分解;会利用分式基本性质进行约分和通分;会进行简单
的分式加、减、乘、除运算。
3、会逆用乘法公式、乘法法则验证因式分解;会用类比的方法得出分式的性质和运算法则;
会用作差法比较两个代数式值的大小。
复习教学过程设计
一、【唤醒】
1、填空题
(1)
(2)因式分解中的公式有 , ,
(3)分式的乘(除)法法则是 ,
分式的加(减)法法则是 ,
2、判断题
( 1 ) 等 式 4)2(3463 222 xxxx 从 左 到 右 的 变 形 是 分 解 因 式
( × )
( 2 ) 只 要 分 式 的 分 子 为 零 , 则 分 式 的 值 就 为 零
( × )
( 3 ) 分 式
1
1
2
2
a
a 有 意 义 , 则 a ≠ ± 1
( × )
3、选择题
( 1 ) 若 7, 10,a b ab 则 22 abba 的 值 应 是
( C )
A.7 B.10 C.70 D.17
因式分解
因式分解的概念
分组分解法
十字相乘法
因式分解的方法
(因式分解方法的选择:一提、二用、三叉、四分组)
分式
分式的运算
分式的概念
分式的基本性质
( 2 ) 下 列 各 式 分 解 不 正 确 的 是
( C )
A、 2 ( )x xy xz x x y z B、 23 2 26 9 3a a b ab a a b
C 、 24 16 2 4 2 4a a a D 、
2 2 2 2 2 22 2x y yz z x y yz z x y z x y z
( 3 ) 分 解 因 式 : 2 4 12x x 的 结 果 是
( C )
A、 3 4x x B、 3 4x x C、 2 6x x D、
2 6x x
( 4 ) 下 列 等 式 成 立 的 是
( D )
A baba
ba
22 B )0(
aam
an
m
n C 2
2
y y
x y x y
D
)0( ama
na
m
n
( 5 ) 化 简 1xx y x
等 于
( C )A 1 B xy C
x
y D
y
x
二、【尝试】
例 1 有这样的一道题:“计算:
2
2 2
2 1 1
1
x x x xx x x
的值,其中 x=2006。”甲
同学把
“ 2006x ”错抄成“ 2060x ”,但他的计算结果也是正确的。你说这是怎么
回事?
解 原式=0 因为化简结果不含 x,所以无论他抄什么值,结果都是正确的。
提炼:如果把 x 的值抄错,而不影响计算结果,这一类题的化简结果一定是一个常数,与 x
的取值无关;
如果把 x 的值抄成它的相反数,而不影响计算结果,这一类题的化简结果一定是一个
常数或者是
关于 x 偶次幂的代数式,与 x 的符号无关。
例 2 化 简
( 1)
2 21 2 1 1
2 2 1
x x x
x x x
( 2) (
22 x
x
x
x ) 4
2
x
x
解 (1)原式=
2
x
x
(2)原式= 1
2x
提炼:(1) 解题时要注意分式的运算顺序,先乘除,再加减,有括号优先,其次能分解的
多项式要分解因式,便于约分,结果一定要是最简分式。
(2)对于 a b c 分配律仍适用,但 c a b 不能用分配律。
例 3 已知:
3 4
1 2 1 2
x A B
x x x x
,求整式 A、B。
分析:由于要求 A、B,等式的左边是已知,右边是未知,可以从未知化到已知。故把等式
作恒等变形,得到等式左右两边分母相同,所以分子也相同,转化为关于 A、B 的一
个二元一次方程组,再求解。
解 A=1 B=2
提炼:本例是分式运算的逆向运用,两个代数式恒等,首先是化结构相同,其次是利用相同
项的系数也相同求未知量。
例 4 甲、乙两人进行百米赛跑,甲前半程的速度为 m 米/秒,后半程的速度为 n 米/秒;乙前
半时的速度为 m 米/秒,后半时的速度为 n 米/秒。问:谁先到达终点?
分析:本题首先要用 m、n 的代数式表示甲、乙两人到达终点的时间 t1、t2,比较 t1、t2 的大
小,可以转化为 t1-t2 与 0 比较
解 见复习指导用书第 16 页
提炼:(1)比较两个代数式 A、B 的值的大小,通常可用作差的方法,当 A-B﹥0,则 A﹥
B;当 A-B=0,则 A=B;当 A-B﹤0,则 A﹤B。
(2)由于本例中没有指明 m、n 的大小,所以要分 m=n 与 m≠n 两种情况讨论。
三、【小结】
1、 带领学生回顾尝试中的填空题。
2、 这节课复习因式分解的应用,化简分式。在化简分式时,注意的运算顺序和符号,防止
出错。其次比较两个代数式值的大小可以用作差法。
四、【实践】
(1)教师自行设计作业 (2)复习指导:14 页第 3 题单数、17 页 3、4
第 5 课时 一次方程 分式方程 一次方程组
居群芳
复习教学目标
1、了解一次方程、分式方程、二元一次方程组的概念。知道方程组的解的含义。理解分式
方程产生增根的原因。理解二元一次方程与一次函数的关系。说出解整式方程和分式方程
的异同,
2、会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程。
3、运用化归思想,引导学生分析出解二元一次方程组的本质是消元。运用方程或方程组解
决实际问题
复习教学过程设计
一、【唤醒】
1、 填空:
2、判断:
(1)
3
1
2
1
x
1 是一元一次方程 ( ) (2)∵ 23 x ∴
2
3x
( )
( 3 ) ∵
1
1
y
x 是 方 程 yx 2 =3 的 解 ∴ 方 程 yx 2 =3 的 解 是
1
1
y
x
( )
(4)方 程组
12
33
yx
yx 的解 是一次函 数 xy 33 与 12 xy 的图 象的交点 坐标
( )
3、选择:
( 1 ) 关 于 的 方 程 012)1( mxm 是 一 元 一 次 方 程 , 则 m 为
( )
A、 1m B、 1m C、 1m D、 1m
( 2 ) 二 元 一 次 方 程 组
5
22
yx
yx 的 解 是
( )
A、
6
1
y
x B、
4
1
y
x C、
2
3
y
x D、
2
3
y
x
( 3 ) 已 知 是 2x 方 程 042 mx 的 一 个 根 , 则 m 的 值 是
方程(组)的应用
分式方程
整式方程
一元二次方程
一元一次方程 解题步骤
二元一次方程组 解法
图像法
方程
解题方法:
是
( )
A、 8 B、—8 C、0 D、2
( 4 ) 已 知 方 程 组
5
4
aybx
byax 的 解 是
1
2
y
x , 则 ba 的 值 为
( )
A、3 B、0 C、 1 D、1
二、【尝试】:
例 1:解方程:
(1) 14
32
3
1 xx (2) 1
1
4
1
1
2
xx
x
解: 略 答案:(1) 5.12x (2) 1x 是增根,原方程无解
提炼:解分式方程与整式方程的方法相似,容易出现错误的地方一是去分母时漏乘整式项及
分子是多项式忘记添括号,二是忘记检验求得的整式方程的解是不是分式方程的根;
例 2: 解方程组
(1)
1323
42
yx
yx (2) 312523 xyyx
解 略 答案(1)
2
3
y
x (2)
3
1
y
x
提炼:解二元一次方程组应先观察方程中相同未知数的系数的特征,如果一个未知数的系数
绝对值为 1,一般选用代入法,若相同未知数系数绝对值相等,一般用加减法。
例 3: 在一次慈善捐款活动中,某同学对甲、乙两班捐款情况进行统计,得到如下三条信
息:信息一:甲班共捐款 300 元,乙班共捐款 232 元;信息二:乙班平均每人捐款钱数
是甲班平均每人捐款钱数的 4
5
倍;信息三:甲班比乙班多 2 人.请你根据以上三条信息,
求出甲班平均每人捐款多少元?
解 略 答案 5 元
提炼:列方程解应用题的步骤是一“审”二“设”三“列”四“解”五“答”。在审题过程
中,要找出等
量关系,设元的方法有两种(直接设元法和间接设元法),列是根据等量关系列出相
应的方程(组),
在解方程时,还要考虑方程的解是否要检验、是否符合实际意义,最后写上答案
例 4:(1)、阅读下列表格,求出表中关于 x 的方程的解。
方 程 方程的解
ccxx 11
cxcx 1, 21
ccxx 11
cxcx 1, 21
(2)、通过阅读上述表格,你能解关于 x 的
方程
1
2
1
2
ccxx 吗?
分析:仔细阅读表格,比较以后不难发现方
程的相似之处。方程左右两边形式完全相
同,只是把其中的未知数换成了某个常数,
那么这样的方程可直接得解,因此我们只要
把
1
2
1
2
ccxx 换成这种形式即可。
解:∵
1
211
21
ccxx
11 cx 或
1
21
cx
1
1, 21
c
cxcx
经检验
1
1, 21
c
cxcx 是原方程的解。
提炼:观察、比较、归纳、猜测是解数学题的重要能力,仔细观察方程结构,将要解的方程
化为材料中的方程的形式,体会类比思想。
三、【小结】
1、知识结构:见填空。2、基本数学思想:化归思想、类比思想、数形结合思想。
四、【实践】
1、教师自行设计作业。2、复习指导用书:第 21 页 3、24 页 15、31 页 9、10、12 题。
第 6 课时 一元二次方程
王爱军
复习教学目标
1、 知道一元二次方程及其相关概念;了解求方程近似解的方法;能说出列方程解应用题的
步骤。
2、 会灵活应用方程解法解简单的一元二次方程。
3、 会利用一元二次方程知识解决有关实际问题,能根据具体问题的实际意义检验结果的合
理性及分类思想。通过复习方程解法,进一步体会转化思想。
复习教学过程设计
一、【唤醒】
1、填空题
2、判断题
( 1 ) 关 于 x 的 方 程 2 21 5 0k x kx 是 一 元 二 次 方 程 , 则 1 0k 且k
ccxx 22
cxcx 2, 21
ccxx 33
cxcx 3, 21
ccxx 44 ____, 21 xx
( 0)m mx c mx c
____, 21 xx
一元二次方程
应用(注意验证解的合理性)
近似解 直接开方法
精确解
( × )
( 2 ) 把 一 元 二 次 方 程 73)12( 2 xx 化 成 一 般 形 式 是 073)12( 2 xx
( × )
( 3 ) 方 程 2 6 5 0x x 的 左 边 配 成 完 全 平 方 后 所 得 方 程 为 23 4x
( × )
3、选择题
( 1 ) 方 程 2 5 7x x 根 的 情 况 是
( B )
A、有两个相等实根 B、有两个不等实根 C、没有实根 D、无法确定
( 2 ) 若 一 元 二 次 方 程 2 1 02x x 两 个 实 数 根 x1 、 x2 , 则
1 2
1 1
x x
的 值 是
( A )
A、 2 B、
2
1 C、
2
1 D、2
(3)关于 x 的一元二次方程 2 7 0x kx 的一个根为 1 1x ,另一根为 2x ,则有
( A )
A 、 26, 7k x B 、 26, 7k x C 、 26, 7k x D 、
26, 7k x
( 4 ) 已 知
2
2
3 2 01
x x
x
, 则 x 的 值 为
( C )
A、1 B、1 或 2 C、2 D、5
二、【尝试】
例 1 用适当方法解下列方程:
(1) 21 2 1 8 02 x (2) 2 29 3 4 2 0x x
(3) 2 12 3 2y y (4) 2 2 2 4 0x x
分析: 结合方程特点,四道题的解法依次是直接开方法、分解因式法、公式法、配方法。
解 略 答案见复习指导用书第 26 页
提炼: 形如 02 cax 的方程,选择用直接开方法;形如 02 cbxx 的方程,左边可
以因式分解,选择用因式分解法;形如 02 cbxx 的方程,如果一次项系数是偶
数,可以选择用配方法;否则用公式法。
例 2 去年,我国政府为减轻农民负担,决定在 5 年内免去农业税.某乡镇去年人均上缴农
业税 25 元,预计明年人均上缴农业税为 16 元,假设这两年降低的百分率相同.
(1)求降低的百分率;(2)若小红家有 4 人,今年小红家减少多少农业税?
(3)小红所在的乡约有 16000 农民,问该乡农民今年减少多少农业税.
分析:例题第(1)小题跨度 3 年,去年、今年、明年,用列表法分析,设降低的百分率是 x ,
去年是 25 元,用 x 表示今年是 25 1 x ,明年是 225 1 x ,然后根据等量关系列
出方程,解出 x 的值;第(2)、(3)题已知 x 的值,分别求代数式 25 4 25 16000x x
的值;
解 略 答案(1)20% (2) 20 元 (3)80000 元
提炼: 运用数学知识解决社会热点问题和实际生活中的问题,关键是理解题意,将实际问
题转化为数学问题。其次本例中的百分率是一个小于 1 的正数。
例 3 有一根长为 68cm 的铝丝,把它剪成 32cm 和 36cm 的两段,用 32cm 的一段弯成一个矩
形,36cm 的一段弯成一个有一条边是 10cm 等腰三角形。请问:能否使弯成的矩形与等
腰三角形的面积相等?若不能,请说明原因;若能,请求出矩形的边长。
解 略 解法参照复习指导用书第 35 页
提炼:(1)例题是一道几何背景面积相等的应用题,包含的知识点有矩形、三角形的周长、
面积,等腰三角形的三线合一、勾股定理以及方程的解法。
(2)三角形一边长是 5cm,这一边是腰还是底边不清楚,所以必须分类讨论。
例 4 阅读下列材料,并回答问题:
解方程 4 26 5 0x x ,这是一个一元四次方程,根据该方程特点,它的通常解法是:
设 2x y ,
则原方程变为 2 6 5 0y y ①,解这个方程,得 1 21, 5y y 。当 1 1y 时, 1x ;
当 2 5y 时, 5x 。所以原方程有四个根 1 2 3 41, 1, 5, 5x x x x
(1)在由原方程到方程①的过程中,利用了 达到了 的目的。
(2)利用上述方法解方程: 22 24 12 0x x x x
分析:阅读材料,体会换元法解高次方程的方法,设辅助未知量,把方程降次,再解一元二
次方程。
解 (1)换元法 降次 (2)设 2x x y ,则原方程变为 2 4 12 0y y ,解这
个方程,得 1 26, 2y y 。当 1 6y 时,即 2 6 0x x 解得 1 23, 2x x ;当
2 2y 时,即 2 2x x , 2 4 7b ac <0 ∴此方程无解。所以原方程有两个
根 1 23, 2x x
提炼:阅读材料,理解解高次方程的一般思路:换元降次,化高次方程为低次方程,体会化
归思想。
三、【小结】
3、 带领学生回顾尝试中的填空题。
4、 本课运用的数学方法有分类思想、化归思想。
四、【实践】
(1)教师自行设计作业 (2)复习指导:28 页 11、14,38 页 20
第 7 课 一元一次不等式(组)
彭淑霞
复习教学目标:
1、 能根据具体问题中的大小关系了解不等式的意义,能说出不等式的基本性质,知道不等
式(组)的解及解集的含义。
2、 会解简单的一元一次不等式,并能在数轴上表示一元一次不等式的解集;会解一元一次
不等式(组),并能在数轴上确定其解集。
3、 能运用类比思想比较一元一次不等式和一元一次方程在解法上的异同点,初步体会数形
结合思想,并能运用数形结合的方法解决与不等式(组)的解集相关的问题。
复习教学过程设计:
Ⅰ.【唤醒】
一、填空:
不等式 不等式的基本性质 解不等式
知识结构(阅读):实际背景 一元一次不等式 解法
一元一次不等式组 解法
1.不等式基本性质:(1)_________________ (2)______________ (3)_______________
2.不等式的解集在数轴上的表示方法:大于向____画,小于向____画,有等号画____,无等
号画______.
3. 解一元一次不等式的一般步骤:(1)______(2)______(3)_____(4)____(5)_____.
4.由两个一元一次不等式组成的不等式组的解集一般有四种类型:
(1) ( )x a a bx b
其解集为_____ ,简记为“同大取______”.
(2) ( )x a a bx b
其解集为______ ,简记为“同小取______”.
(3) ( )x a a bx b
其解集为______, 简记为“大小小大取_____”.
(4) ( )x a a bx b
其解集为_______, 简记为“大大小小_____”.
二、判断:
1 . 由 2 3a 得 a 3
2
( ) 2. 由 2 0a 得 2 a
( )
解集
数轴表示
解集
数轴表示
解集
数轴表示
3. 由 a b 得 a m b m ( ) 4. 1 12 得 1
2 a a
( )
5. 2x 是不等式3 6x 的一个解 ( ) 6. 满足不等式 3 5x 的整数解有 7
个. ( )
三、选择:
1 . 已 知 a b , 则 下 列 变 形 中 错 误 的 是
( )
A. 2 2a b B. 3 3a b C.
2 2
a b D. 1 1a b
2. 不 等 式 33
1 x 的 解 集 是
( )
A. 9x B. 9x C. 1x D. 1x
3. 不 等 式 19 3 4x 的 非 负 整 数 解 的 个 数 为
( )
A. 4 个 B. 5 个 C. 6 个 D. 无数个
4 . 不 等 式 2 3a x 的 解 集 为
2
3
ax , 则 a 的 取 值 范 围 为
( )
A. 2a B. 2a C. 2a D. 2a
Ⅱ. 【尝试】
例 2. 解不等式 6 3
4
3 2
x x
,并把它的解集在数轴上表示出来。
解略。(答案: 3x )
例 3. 解不等式组
2 4
1 2
1
4
x x
x
x
,并求出其整数解。
分析:解一元一次不等式组既不能用代入法也不能用加减法,而是分别求出不等式组中的每
个不等式的解集,然后利用数轴找出它们解集的公共部分,即不等式组的解集,熟练
以后也可以利用口诀“同大取大,同小取小,大小小大取中间,大大小小无解”简捷
地确定不等式组的解集。最后结合数轴用列举法确定符合条件的特殊解。
解略。(答案: 3
1
2
x ,整数解为 1)
提炼:用数形结合的思想方法,根据不等式组的解集的概念结合数轴正确确定不等式组的解
集及特殊解。
例 4. 若不等式组 8 4 1x x
x m
的解集为 3x ,求 m 的取值范围。
分析:首先将不等式组化为 3x
x m
,再利用数轴或依据不等式“同大取大”的方法可知 3m 。
提炼:利用不等式组的解集来确定字母的取值范围,往往需要逆用不等式组的解集,有时需
借助数轴或讨论等手段来解决问题。
例 5. 阅读第(1)题的解法,解答第(2)题。
(1) 解不等式 2 3x
解:① 当 2 0x 即 2x 时, 2 3x ,所以 5x 。
② 当 2 0x 即 2x 时, 2 3x ,所以 1x 。
综上所述,原不等式的解集为 5x 或 1x 。
(2) 根据以上解法和不等式的性质“若 2 2a b ,则 a b ”解不等式 2( 1) 4 0x 。
分析:阅读第(1)题理解其解题方法:根据绝对值的概念先化简绝对值,再解一元一次
不等式。
解略(答案: 3x 或 1x )
提炼:运用绝对值的概念化简绝对值,将含绝对值的不等式转化为一元一次不等式,体
会分类思想。
Ⅲ.【小结】:
1.本单元知识结构(见填空第 1 题)
2.本节课运用的数学思想方法:类比思想、数形结合思想、分类思想等。
Ⅳ.【实践】
1.教师自行设计作业。
2.复习指导用书第 34 页第 1、3 题。
第 8 课时 不等式(组)的应用
彭淑霞
复习教学目标:
1. 初步认识一元一次不等式(组)的应用价值,知道在一定条件下的实际问题可以抽象为
不等式(组)的问题,并认识到实际问题对不等式(组)的解集的影响,知道一元一次
不等式与一次函数有密切的关系。
2. 能根据具体问题中的数量关系列出一元一次不等式(组),通过解一元一次不等式(组)
解决简单的实际问题,并能根据具体问题检查结果是否合理,能通过解一元一次不等式
解决简单的一次函数问题。
3. 类比列方程(组)解应用题的方法经历列一元一次不等式(组)解实际问题的建模过程,
体会转化思想,通过解一元一次不等式解决函数问题体会数形结合思想和分类思想。
复习教学过程:
Ⅰ.【唤醒】
一、填空:
列一元一次不等式(组)解决实际问题的一般步骤类似于列方程组解应用题的一般步骤,
可分为
( 1 ) _________ ( 2 ) 根 据 不 等 关 系 列 不 等 式 ( 组 ) ( 3 )
____________(4)__________(5)___________.
二、判断:
1. 一个两位数,十位数字与个位数字的和为 6,若这两个两位数不大于 42,若设此两位数
的 个 位 数 字 为 x , 则 不 等 式 可 列 为 ( 6- x ) + x ≤ 42 。
( )
2. 某商店将一个进价 80 元,标价为 120 元的商品打折销售,要使得利润率不低于 5%,最
多 可 打 几 折 ? 若 设 可 打 x 折 , 则 不 等 式 可 列 为 120 x -80 ≥ 80 × 5 % .
( )
三、选择:
1 . 使 代 数 式 3
4
2
x 的 值 不 大 于 3 5x 的 值 的 x 的 最 大 整 数 值 为
( )
A. 7 B. 6 C. 4 D. 不存在
2.长度为 3cm、7cm、 x cm 的三条线段要能围成一个三角形,则 x 的取值范围为
( )
A. x <10 B. x >4 C. 4< x <10 D. 无法
确定
3.小新准备用 20 元钱买钢笔和笔记本,钢笔每支 3 元,笔记本每本 2 元,他买了 3 本笔记
本 , 则 他 最 多 还 可 以 买 钢 笔
( )
A. 6 支 B. 5 支 C. 4 支 D. 3 支
Ⅱ.【尝试】
例 1.某校校长暑期将带领该校市级三好学生去北京旅游,甲旅行社说:“如果校长买全票
一张,则其
余学生可享受半价优惠。”乙 旅行社说:“包括校长在内全部按全票价的 6 折优惠(即
按全票价的
60%收费)。”若全票价为 240 元。
(1)设学生数为x 名,甲旅行社收费为 1y 元,乙旅行社的收费为 2y 元,分别计算两家旅行社的收费
(建立表达式)。
(2)当学生数是多少时,两家旅行社的收费一样?
(3)就学生数 x 讨论哪家旅行社更优惠。
分析:根据两家旅行社的收费情况构建出一次函数的模型,再根据题意列出不等式求解。也
可以画出两个一次函数的图象,通过观察图象比较哪家旅行社更优惠。
解答过程见复习指导用书第 33 页。
提炼:在讨论哪家旅行社更优惠时,不能只选特殊的数据代入选择,而要分类讨论。本题主
要反映了函数和不等式的关系。本题运用的数学思想方法有分类思想、数形结合思想
等等。
例 2.幼儿园将若干件玩具分给小朋友,如果每人分 3 件,那么还余 59 件;如果每人分 5
件,那么最后一人还少几件,该幼儿园有多少件玩具?有多少个小朋友?
分析:设幼儿园有 x 个小朋友,由每人分 3 件,那么还余 59 件可知:共有玩具数(3 x +59)
件。
由每人分 5 件,则最后一人还少几件可知:
(1) x 个小朋友每人分 5 件时玩具数不够,即需要的玩具数>现有的玩具数。
则不等式可列为 3 x +59>5( x -1)。
(2)( x -1)个小朋友每人分 5 件时玩具数有剩余,即需要的玩具数<现有的玩具数。
则不等式可列为 3 x +59<5 x 。(解答过程见复习指导用书第 33 页。)
提炼:列不等式组解应用题的步骤与列方程组解应用题的步骤类似,不同的是后者寻求的是
等量关系,列出的是等式;前者寻求的是不等关系,列出的是不等式,并且解不等式
组所得的结果通常是一解集,需要从解集中找出符合题意的答案。
例 3.某厂用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素 C 含量及购买这两
种原料的价格如下表:
原料
维生素及价格 甲种原料 乙种原料
维生素 C/(单位/千克) 600 100
原料价格/(元/千克) 8 4
现配制这种饮料 10 千克。
⑴ 如果要求饮料至少含有 4200 单位的维生素 C,试写出所需甲种原料 x (千克)应满
足的不等式。
⑵ 在⑴的条件下,如果还要求购买甲、乙两种原料的费用低于 72 元,那么应在什么范围内购
买甲种原料?
分析:① 由“用甲、乙两种原料配制成某种饮料,现配制这种饮料 10 千克。”可知:现所需甲
种原料为 x 千克,则所需乙种原料为(10- x )千克。 x 千克甲种原料中维生素 C 的含量
为 600 x 千克,(10- x )千克乙种原料中维生素 C 的含量为 100(10- x )千克,由题意
得:可得:600 x +100(10- x )≥4200。
② x 千克甲种原料的价格为 8 x 元,(10- x )千克乙种原料的价格为 4(10- x )元,
则购买甲、乙两种原料的费用为:8 x +4(10- x )元,由题意得:8 x +4(10- x )<72.
从而建立不等式组 600x+100(10-x) 4200
8x+4(10-x)<72
。此不等式组的解集为 6.4≤ x <8.
提炼:本题为调配问题。
例 4.认真阅读对话:
小明:“阿姨,我买一盒饼干和一袋牛奶。”(递上 10 元钱)
售货员:“小朋友,本来你用 10 元钱买一盒饼干是多的,但要再买一袋牛奶就不够了。
今天是儿童节,我给你的饼干打 9 折,两样东西请拿好,还有找你的 8 角钱。”
请你根据对话的内容,试求出饼干和牛奶的标价是多少元(注:饼干的标价是整数元)?
分析:设饼干的标价为 x 元。由“本来你用 10 元买一盒饼干是多的”可建立不等式 x <10;由
“我给你的饼干打 9 折,两样东西请拿好,还有找你的 8 角钱”可知牛奶的标价为
(10-0.8-90% x )元,由“本来你用 10 元钱买一盒饼干是多的,但再买一袋牛奶就不够
了”建立不等式: x +(10-0.8-90% x )>10,
从而列出不等式组,再由“饼干的标价是整数元”在不等式组的解集中找出整数解。
解略。(答案:饼干的标价为 9 元,牛奶的标价为 1.1 元)
提炼:列不等式(组)解应用题的关键是寻找不等关系,再由不等关系列出不等式(组),
因此要善于挖掘题中隐含的不等关系。
Ⅲ. 【小结】
1. 列不等式(组)解实际问题的一般步骤(见填空)
2. 本节课运用的数学思想方法有数形结合思想、类比思想、转化思想、分类思想等。
Ⅳ. 【实践】
1. 教师自行设计作业。
复习指导用书第 34 页第 18、19、20 题。
第 9 课时 函数概念、一次函数
陈淑峰
复习教学目标
1、能根据具体问题中的数量关系和变化规律了解函数、一次函数的意义。能说出函数的三
种表示方法、一次函数的基本性质,知道函数图象的画法。
2、能画简单的一次函数图象,并根据已知条件确定一次函数的表达式。
3、能运用类比思想比较函数、一次函数和正比例函数的异同点,初步体会数形结合思想,
并能运用数形结合的方法解决有关实际问题,并尝试用函数的方法描述有关实际问题,对变
量的变化规律进行初步预测。
复习教学过程设计
1、【唤醒】
一、填空
(1 ) 写 出下 列 函 数 中 自变 量 x 的 取 值范 围 。
2
1
xy , 2 xy ,
2
1
x
y 。
(2)已知 1y 与 x 成正比例,且 2x 时, 4y ,那么 y 与 x 之间的函数关系式为
_________________。
(3)直线 12
1 xy 与 x 轴的交点坐标为(_______),与 y 轴的交点坐标为(_______)。
(4)根据下列一次函数 y=kx+b(k≠0)的草图回答出各图中 k、b 的符号:
二、选择
(1)下列函数中,表示一次函数的是
( )
A、 23 2 xy B、 )0(2
kx
ky C、
5
32 xy D、
12
3
x
xy
(2)已知一次函数 y=kx+b,y 随着 x 的增大而减小,且 kb<0,则在直角坐标系内它的大致图
象是( )
2、【尝试】
例 1、已知一次函数的图象经过点 )6,1(A 、 )2,1(B ,(1)求函数解析式;(2)画出函数
图象;(3)函数的图象经过那些象限?(4)当 x 增大时, y 的值如何?
解略(答案: 42 xy ,图略,图象经过一、二、四象限, y 随 x 增大而减小)
例 2、已知一次函数 )3()2( nxmy
(1)当 m、n 取何值时,y 随 x 的增大而增大?
(2)当 m、n 取何值时,直线与 y 轴的交点在 y 轴的下半轴?
(3)当 m、n 取何值时,直线经过一、二、四象限?
分析:(1)一次函数 )0( kbkxy 的性质:当 0k 时, y 随 x 的增大而增大;(2)直
线 )0( kbkxy 与 y 轴的交点坐标为 ),0( b ;(3)当 0k 且 0b 一次函数的图象经过
一、二、四象限。
解略(答案:(1) 2m ,n 为一切实数;(2) 32 nm 且 ;(3) 32 nm 且 )
提炼:利用逆向思维的方法,根据一次函数的性质,体会逆向思维和定向思维的异同。
例 3、已知:函数 y=(m+1)x+2m﹣6
(1)若函数图象过(﹣1,2),求此函数的解析式。
(2)若函数图象与直线 y=2x+5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与此同时 y=﹣3x+1 的交点并求这两条直线与 y 轴所围成的
三角形面积。
分析:(1)利用函数的表达式与点的坐标的关系;(2)一次函数图象平行,表达式之间的
关系;(3)利用点的坐标求线段的长,确定三角形的底和高求三角形的面积。
解:(1)由题意:2=﹣(m+1)+2m﹣6
解得 m=9 ∴ y=10x+12
(2) 由题意,m+1=2 解得 m=1 ∴ y =2x﹣4
(3) 由题意得解得: x=1,y=﹣2 ∴ 这两直线的交点是(1,﹣2)
13
42
xy
xy
y=2x﹣4 与 y 轴交于(0,-4) y=﹣3x+1 与 y 轴交于(0,1)
∴S△=
2
5 提炼:利用数形结合的思想方法,根据函数的性质结合图形确定函数的解析式及三
角形的面积。
例 4、如图,l 甲、l 乙两条直线分别表示甲走路与乙骑车(在同一条路上)
行走的路程 S 与时间 t 的关系,根据此图,回答下列问题:1)乙出发时,与
甲相距 10km;2)行走一段时间后,乙的自行车发生故障停下来修理,修车时
间为 1h;
3)乙从出发起,经过 2.5h 与甲相遇;4)甲的速度为 5km/h,乙的速度为 15km/h;
5)甲行走的路程 s(千米)与时间 t(小时)之间的函数关系式是 s=5t+10(t≥0);
6)在 0h
2.5h 甲走在乙的后面;
7)如果乙的自行车不出故障,则乙出发后经过 1h 与甲相遇,相遇后离乙的出发点 15km;在
0h1h 范围内甲走在乙的后面;并在图中标出其相遇点。
(相遇点为 A)
提炼:运用函数的图象及性质解决实际问题,并对某些实际问题进行比较、预测,体会生活
中的数学。
3、【小结】
(1)本单元知识结构(见唤醒阅读)
(2)本节课运用的数学思想方法:类比思想、数形结合思想、猜想。
4、【实践】
(1)教师自行设计作业。(2)复习指导用书第 48 页第 11 题,第 53 页第 12、13 题。
第 10 课时 反比例函数
陈 波
复习教学目标:
1. 结合具体情景体会反比例函数的意义,能根据已知条件确定反比例函数的表达
式.
2. 会画反比例函数的图象,并能根据图象探索并理解反比例函数的性质,进一步提
高从函数图象中获取信息的能力.
3. 会用反比例函数解决某些实际问题,逐步形成用函数观点处理问题的意识,体验
数形结合的思想方法.
复习教学过程设计:
Ⅰ【唤醒】
一、填空
1、在式子(1) 13 xy (2) 13 xy (3)
3
1
xy (4) 13 xy (5)
xy 2
3 中
哪些是反比例函数
2、反比例函数
x
ky (k 不为 0)的图象既是 对称图形,又是 对
称图形
3、函数
xy 1 其图象位于第 象限,在其图象所在象限内,y 随着 x 的增大
而 ,当 0x 时,y 0
4、函数
xy 100
7 的图象位于第 象限,在其图象所在象限内,y 随着 x 的增
大而 当 x<0 时,y 0
5、反比例函数的图象经过点(2,3),则点(-2,-3) 该函数图象上(填“在” 或
“不在”)
二、选择
1、如果反比例函数
x
ky 的图象经过点 P(-3,2),那么 k 的值是( )
A、6 B 、
2
3 C、
3
2 D、-6
2、已知 P(-6,3)在函数 的图象上,那么下列的点不在该函数的图象上的是 ( )
A、(-3,6) B、(
3
1 ,-54) C、(3,-54) D、(-4 ,
2
14 )
3、若函数
x
ky 3 的图象位于第一,三象限内,则 k 的取值范围( )
A、k>3 B、k <3 C、k>0 D、k<0
4、点(-2,y1) 、(-1,y2)、 (1,y3)都在反比例函数
xy 1 的图象上,则下列关
系式成立的是( )
A、y1>y2>y3 B、y1<y2<y3 C、y3 >y1> y2 D、 y1> y3> y2
5、如图
xy 2 的图象上有三点 A、B、C,过三点分别作坐标轴的
垂线,分别得到矩形 A1AA2O,矩形 B1BB2O ,矩形 C1CC2O,设这三个矩形
的面积分别为 S1、 S2、S3 则三者的大小关系( )
A、S1>S2 > S3 B、S1<S2 <S3
C、S1 = S2=S3 D、不能确定
Ⅱ【尝试】
例题 1、已知反比例函数的图象过(1,2),求这个函数的解析式,并
画出函数的图象。
解略 (答案:
xy 2 )
例题 2、一蓄水池的排水管每小时排水 10M3,6h 可将满池的水全部排空,如果将排水管每小
时的排水量改为 Qm3,排空水池的水所需要的时间为 t h。
(1) 写出 t 与 Q 间的函数关系式,并画出草图。
(2) 若要将满池的水在 4 小时内排空,那么每小时的排水量 Q 至少为多少?
(3) 如果每小时的排水量为 4m3,那么将满池水排空需要多长的时间?
解略 (答案 (1)
tQ 60 图象位于第一象限 (2) Q 至少要 15 m3 (3)t=15h)
提炼:把实际问题抽象成数学知识,分析变量之间的关系,
建立反比例函数模型,解决问题。注意实际问题中变量的取值要符合
实际。
例题 3,反比例函数
xy 8
1 与一次函数 22 xy 的图象交于 A,B
两点,
(1)求 A,B 两点的坐标,
(2)求 三角形 AOB 的面积
(3) 当 x 取何值时,y1>y2
分析:将问题转化成求 0822 xx 的解,即求出点的横坐标。 利
用分割法求三角形的面积。(答案 A(-2,4) B(4,-2) 三角形 AOB 的面积为 6
当 02 x 或 4x 时, y1>y2 )
提炼:利用数形结合的思想,体会图象的交点坐标与一元二次方程的解的关系。
例题 4、已知反比例函数
x
ky 的图象过(-1,2),直线 bxy 经过第一,三,四象限,
若直线 bxy 与反比例函数
x
ky 的图象只有一个公共点,求 b 的值。
分析:把点的坐标代入函数表达式求 k 的值,把问题转化成一元二次方程 022 bxx
求有两个相同根的情况,并结合一次函数图象特点求 b 的值。(答案: 22b )
提炼:利用数形结合思想,体会函数图象的交点个数与一元二次方程根的个数的关系。
Ⅲ【小结】
1、 本单元知识结构
反比例函数 图象和性质 反比例函数的应用
2、 本节课运用的数学思想方法:数形结合思想
Ⅳ【实践】
1、 教师自行设计作业
复习指导用书 P58 19 、20
第 11 课 二次函数
史栋新
复习教学目标
1. 根据具体情境分析和建立两个变量之间的二次函数关系,能用表格、表达式、图象
表示变量之间的二次函数关系,并能根据具体问题,选取适当的方法表示变量之间的二次函
数关系。
2. 能根据二次函数的表达式确定二次函数的开口方向,对称轴和顶点坐标;会作二次
函数的图象,并能根据图象对二次函数的性质进行分析,逐步积累研究函数性质的经验。
3. 理解一元二次方程与二次函数的关系,并能利用二次函数的图象求一元二次方程的
近似根,并能利用二次函数的相关知识解决实际问题。
复习教学过程设计
Ⅰ.【唤醒】
一、 填空
二次函数的知识结构(阅读)
一元二次方程的近似根利用二次函数的图象求
数的关系一元二次方程和二次函数一元二次方程和二次函
点坐标公式二次函数的对称轴和顶
二次函数的图象
用多种方式表示
二次函数的定义
实际问题情境
二次函数所描述的关系
二次函数
cbxaxykhxay
caxyaxy
xyxy
2,2)(
2,2
2,2
1.函数 22
)2( mxmy ,当 m_____时,该函数是二次函数;当 m_____时,该函数是一
次函数。
2.抛物线 y=2x2+1 的顶点坐标是______,对称轴是 ,当 x= 时,函
数取得最 ___值为 ;二次函数 y=2x2-8x+1 的顶点坐标是______,对称轴是
___________,它的图象是由函数 y=2x2+1 沿着____轴向____平移______个单位,然后再沿
着____轴向____平移______个单位得到。
二、 判断下列函数表达式中哪能些是二次函数(是二次函数打“√”若不是则打“×”)。
(1)y=3x-2 ( ) (2)y=2x2-3x3 ( )
(3)y=1-2x2 ( ) (4) y= 22 x ( )
(5)y= 31
2
x
( ) (6) cbxaxy 2 ( )
三、 选择
1.二次函数 y=ax2,当 a<0 时,y 的值恒小于 0,则自变量 x 的取值范围( )。
A. x 可取一切实数 B. x>0
C. x<0 D. x≠0
2.抛物线 y=2x2+x-3 与 x 轴两个交点间的距离为( )。
A. 2.5 B. -0.5 C. 0.5 D. -2.5
3.有一个二次函数,它的图象经过(1,0);图象的对称轴是 x=2;并且它的顶点与
x 轴的距离是 4,则该函数的表达式是( )
A . 4)2(4 2 xy B. 4)2(4 2 xy C. 4)2(4 2 xy D.
4)2(44)2(4 22 xyxy 或
Ⅱ. 【尝试】
例 1.已知二次函数 y=x2+bx+c 的图象经过(1,0)与(2,5)两点
(1) 求这个二次函数的解析式
(2) 作出该函数的图象,并根据图象回答下列问题:
1 函数的对称轴、顶点坐标、与 x 轴的交点坐标
2 当 x 取何值时,y>0,当 x 取何值时,y 随 x 的增大而减小?
解略 (答案: y=x2+2x-3)
提炼:用待定系数法求二次函数解析式,用描点法作出图象,根据图象解决二次函数的
一些基本性质。
例 2.函数 y=ax2-ax+3x+1 的图象与 x 轴有且只有一个交点,求 a 的值和交点坐标,
求 a 的值和交点坐标。
1. 解略 (答案: 0,(-
3
1 ,0);1,(-1,0);9,(
3
1 ,0) )
提炼:解决函数问题时,先要注意对函数中首项系数 a 的讨论,然后若有二次函数与
x 轴交点的关系,则需利用到二次函数与一元二次方程的关系,利用一元二次方程的根的判
别式来解决。
例 3.阅读下面的文字后,解答问题:
有这样一道题目:“已知二次函数 y=ax2+bx+c 的图象经过点 A(0,a),B(1,
-2), 。求证:这个二次函数图象的对称轴是直线 x=2。”题目中的矩形部分是
一段被墨水污染了无法辨认的文字。
(1)根据现有的信息,你能否求出题目中二次函数的表达式?若能,写出求解过程;
若不能,说明理由。
(2)请你根据已有的信息,在原题中的矩形框内,填加一个适当的条件,把原题补充
完整,并把你所补充的条件填写在原题中的矩形框内。
解略 (答案:(1)y=x2-4x+1, (2)答案不惟一,如填“C(0,1)”或“顶
点纵坐标为“-3”等)
提炼:学生自己编题,有助于学生加深对题意的理解。另外,解决此类问题,是从题
目中的结论到已知条件,有利于训练学生的逆向思维。
例 4.阅读如下材料,运用材料中的知识解决问题
材料:一元二次方程,ax2+bx+c=0(a≠0)有两个实数根 x1、x2,根与系数有如下关
系:
x1+x2=-
a
b ,x1、x2=
a
c ,这个关系称为韦达定理。
问题:二次函数 y=-x2-(m-3)x+2(m-1)的图象与 x 轴交于 A,B 两点(点 A 在原
点 O 的左侧,点 B 在 O 的右侧),且 x1 〈 x2,也 y 轴交于点 c,线 OA 与 OB 的长的乘积等
于 8,求抛物线的顶点 P 及点 C 的坐标。
解略 (答案: P(-1,9), C(0,8) )
提炼:应用韦达定理解决二次函数问题,可以将二次函数的问题转化为一元二次方程
来解决,体会方程与函数的关系。
Ⅲ. 【小结】
1. 本单元知识结构(见填空第 1 题)。
2. 本节课运用的数学思想方法:类比思想、数形结合思想、分类思想等。
Ⅳ. 【实践】
1、 师自行设计作业。2、复习指导用书 P61—63。
第 13 课时 平行线、三角形与证明
朱淑芳
复习教学目标:
1、 知道补角、余角、对顶角、同位角、内错角、同旁内角的概念,能根据图形或数量关系
判断两个角之间的关系,知道三角形三边之间的关系、三角形的内角和定理及三角形的
内角、外角、中线、高、角平分线等概念;知道平行线的概念及性质及两直线平行的条
件;知道全等三角形的概念、性质及三角形全等的条件;知道角平分线、线段垂直平分
线的概念及性质。
2、 会求一个角的补角、余角,并能利用补角、余角的性质计算或证明;会根据三角形的有
关概念计算或证明;会利用平行线的性质计算或证明;会利用全等三角形的概念性质及
两个全等三角形全等的条件等解决问题,会利用角平分线及线段垂直平分线的概念、性
质解决问题。
3、 能综合应用所学知识解决问题.
复习教学过程设计:
一、【唤醒】
1、 填空:
(1)如图,AB∥CD,∠1=38°,则∠2= ∠3=
∠4=
(2)△ABC 中,AB=3 BC=5,则 AC 的取值范围是
(3)△ABC 中,∠A=30° ∠B-∠C=20°,则∠B= ∠C=
(4)添加条件,使线段满足题意:
①、 ,AD 为△ABC 的中线
②、 ,BE 为△ABC 的高
③、 ,CF 为△ABC 的角平分线
(5)已知,OP 平分∠AOB,D 为 OP 上一点,DE⊥OA 于 E,
DF⊥OB 于 F,OD=5,DE=3,则 DF= OF=
若连接 EF,则 OD 与 EF 的关系是
2、判断
(1)若∠A 与∠B 是同旁内角,则∠A+∠B=180° ( )
(2)若∠α与∠β是互为余角,则∠α+∠β=180° ( )
(3)若∠1=∠2,则∠1 与∠2 是对顶角 ( )
(4)若两个三角形有两条边及一个角对应相等,则这两个三角形全等 ( )
3、选择
(1) 如图,AB∥DE,∠E=65°,则∠B+∠C 的度数是( )
(A)135° (B)115° (C)65° (D)35°
(2) 如图,D、E 分别为△ABC 的中点,BC=8 ∠A=41°,
∠B=48°则下列结论正确的是( )
(A)DE=4,∠AED=41°(B)DE=4,∠AED =81°
(C)DE=4,∠AED=48°(D)DE=4,∠ADE=48°
(3)一个角的补角与它的余角的和比这个角的 2 倍少 30°,则这个角等于( )
(A)30° (B)45° (C)60° (D)75°
二、【尝试】
例 1.已知:直线 a∥b,A、B 为直线 a 上两点(点 A 在 B 的左边),C、D 为直线 b
上两点(点 C 在点 D 的左边),AB=CD,画出图形,并连接 AD、BC,设交点为 O,写出
图中所有的全等三角形,并选一对加以证明。
分析:首先按题意画出符合要求的图形,由 a‖b、AB=CD 得到四边形 ABCD 为平行四边形,
然后根据平行线的性质得到相等的角,再根据三角形全等的条件得到答案。
解略 (答案:△ABD≌△DCA △ABC≌△DCB △AOB≌△DOC △AOC≌△
DOB)
提炼:本题考查平行线的性质及三角形全等的条件,并且涉及读句画图等知识。
例 2.例 1 中,若其他条件不变,把“AB=CD”该为“AC=BD”,则上述所得结论都
还一定成立吗?写出仍能成立的,若有不能成立的,画图说明。
分析: 先按题意画出符合要求的图形,并考虑情况的多样性,进一步应用三角形全等的条
件。
解略 (答案:△ABD≌△DCA 、△ABC≌△DCB 、△AOC≌△DOB,其中△AOB≌△
DOC 不一定成立)
提炼:本题主要说明“SSA”不能说明三角形全等,同时考虑情况的多样性。
例 3.如图,△ABC,△EDC 都是等腰直角三角形,且点 C 在 AD 上,AE 的延长线与
P
BD 交于点 F,请在图中找出一对全等三角形,并写出证明全等的过程。
分析:由等腰直角三角形的定义可得 AC=BC,DC=EC,再由∠ACB=∠DCE 可得△ACE≌
△BCD
证明略
提炼:本题考查等腰三角形的定义及三角形全等的条件,也考查学生在复杂问题中
寻找所需图形的能力
例 4.如图,AB=AE,∠ABC=∠AED,BC=ED,点 F 是 CD 的中点。
(1)求证:AF⊥CD
(2)在你结论证明完毕后,还能得出什么新结论,请写出三个(不要证明)
分析:连接 AC、AD,AB=AE,∠ABC=∠ADE BC=ED 得△ABC≌△AED,得
AC=AD , 又 F 是 CD 的中点 , 所以 AF⊥CD。
证明略
提炼:本题考查学生由已知条件构造三角形,用三角形全等的条件得全等三角形,并考查等
腰三角形的性质。
三、【小结】:本节课主要复习了角与角在大小和位置上的关系,并复习了平行线的性质和
条件,同时也复习了三角形全等的条件和性质,并能综合应用。
四、【实践】:1.教师自行设计 2.复习指导 P77 、 12 P79、6、8、10、13
第 14 课时 特殊三角形
彭云
复习教学目标:
1、 知道等腰三角形和等边三角形的性质和判定;了解直角三角形的概念;知道直角三角形
的性质和判定直角三角形的条件;能说出线段中垂线的性质.
2、 会用等腰三角形的性质和判定进行有关的计算和证明;会用直角三角形的性质进行简单
计算;能写出一个命题的逆命题;会用勾股定理解决简单计算,并会用它的逆定理判定
直角三角形;会用“HL”定理判定直角三角形全等。
3、 能用分类讨论的思想解决等腰三角形中的有关计算、用转化的思想将不规则图形转化为
规则图形.
复习教学过程设计
Ⅰ、【唤醒】
一、填空
性质:两腰相等、等边对等角、
等腰三角形 判定
+ 等边三角形 性质
特殊三角形 判定
性质
直角三角形 判定
含 30 角的直角三角形的性质:
等腰直角三角形
直角三角形全等的特殊判定方法是: 线段垂直平分线的性质:
二、 判断:
1、两底角相等的三角形是等腰三角形.( )
2、等腰三角形一定不是钝角三角形.( )
3、等腰三角形中,有一个角是 50°,那么它的底角必是 65°.( )
4、等腰直角三角形底边上的高等于底边的一半.( )
5、如果原命题是假命题,那么它的逆命题一定是假命题.( )
6、有两边对应相等的直角三角形是全等三角形.( )
三、选择:
1、等腰三角形的一边长是 10cm,另一边长是 6 cm,则它的周长是 ( )
A、26 cm B、22 cm C、16 cm D、22 cm 或 26 cm
2、已知一个直角三角形的两边长分别是 3 和 4,则第三边的长是( )
A、4 B、5 C、 7 D、5 或 7
3、如图,在 Rt△ABC 中,斜边 AB 的垂直平分线分别交 AB、AC 于点 E、D,∠A=15°,若 AD=4,
则 BC= ( )
A、4 B、2 C、1 D、 2
4、等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为 ( )
A、75°或 15° B、30°或 60° C、75° D、30°
5、直角三角形斜边上的中线和面积分别是 5 cm ,20 cm2,则它的斜边上的高是 ( )
A、3 cm B、4 cm C、5 cm D、2
Ⅱ、【尝试】
例 1:已知,在△ABC 中,AB=AC,点 M,N 在 BC 上,且 AM=AN,请你用最简便的方法说明 BM=CN 。
分析:作底边上的高,灵活运用“三线合一”性质
证明:略
提炼:究竟作角平分线还是作高或中线,要依具体问题。
例 2、已知:如图,在△ABC 中,D 是 BC 边上的中点,DE⊥AB,DF⊥AC,垂足分别为 E,F,且 DE=DF,
求证:AB=AC
(提示:先用“HL”证△BDE≌△DFC,然后运用“等角对等边”得证)
证明:略
提炼:在直角三角形中会灵活运用“HL”定理
例 3:如图,已知在△ABC 中,AD、CE 是高,且 AE=3,BE=2,CE=4,在不添加任何辅助线和
字母的条件下,你能得到哪些正确结论?(分别从边、角、三角形相似三
个角度去思考)
分析:首先从高和一些线段的长的角度去思考,由直角三角形中的边联想
到运 用勾股定理求出 AC、AD、BC、DE,然后利用等腰三角形、直角三角形,三角形
相似等有关知识逐步得到结论。
解:①AB=AC,②BD=CD=DE,③AD=BC,④∠ABC=∠ACB=∠BED,⑤∠BDE∠=BAC, ⑥
∠BAD=∠CAD=∠BCE=∠CED,⑦∠ACE=∠ADE,⑧∠ACD+∠ AED=180°, ∠BAC+∠CDE=180°,
⑨△BAD≌△CAD,⑩△BAD∽△BCE,⑾△CAD∽△BCE,⑿△BDE∽△BAC
提炼:注意仔细分析已知条件,思考哪些已知条件组合在一起可以产生新的结论及可能产生
的新的结论。
例 4:如图,在四边形 ABCD 中,AB=AD=4,∠A=60°,∠D=150°,CB⊥AB,
已知四边形 ABCD 的周长为 16,求 S 四边形 ABCD
分析:不规则图形往往转化为规则图形,若连接 BD 后,由 AB=AD=4,
∠A=60°容
易判断△BAD 是等边三角形,并且得到△BDC 是含 30°角的直角三角形,
那么 S 四边形 ABCD=S △ABD+S△CBD,根据已知条件可算到 CD+BC=8,然后根据 2CD=BC 可求出 CD,BC。
解: 连接 BD,则△BAD 为等边三角形,∴AD= BD=4,∠ADB=60°,CD+BC=8
又∠ADC=150°,∴∠BDC=90°,∠DBC=30°
在 Rt△BDC 中可求得 CD=
3
8 ,BC=
3
16 ,BD=BC*cos30°=
3
8 3
∴S 四边形 ABCD= S △ABD+S△CBD=
2
1 ×4×2 3 +
2
1 ×4×
3
8 3 =4 3 +
3
16 3 =
3
28 3
提炼:运用“转化”的数学思想将不规则图形转化为规则图形,注意在等边三角形和直角三
角形中运用其性质灵活求解三角形的边长。
变式: 在四边形 ABCD 中,AB=AD=4,∠A=60°,∠D=150°,四边形 ABCD 的周长为 16,又该
如何求
S 四边形 ABCD?
分析:注意在直角三角形中常用勾股定理建立方程求边长。
如:设 CD=x,则 BC=16-4-4-x=8-x
在 BDC 中,有 BC2=BD2+DC2,即(8-x)2=x2+42,解得 x=3。∴CD=3,BC=5.(略)
Ⅲ、【小结】
1、 本节课主要内容:见唤醒中的“知识结构图”。
2、 分类讨论的思想、(如:在等腰三角形中,若已知一个角求另外两个角或已知一边求另
外两边,通常要分类讨论)、数形结合的思想,转化的思想等。
Ⅳ、【实践】
(1) 教师自行设计作业;
(2) 复习指导用书第 83--86 页第 1、3、4、9、13、14、19、22、25、26 题。
第 15 课时 多边形、平行四边形和证明
彭云
复习教学目标:
4、 能说出多边形的内角和定理和外角和定理;知道平行四边形的性质和判断;
5、 会求多边形的内角和,并能判定一个多边形是几边形;会进行有关平行四边形的边角的
简单计算;能运用性质和判定进行相关的证明;能识别中心对称图形。
3、能用数形结合的思想解决平行四边形中的计算和证明。
复习教学过程设计
Ⅰ、【唤醒】
一、填空 内角和定理:n 边形的内角和等于
1、 多边形的有关性质 外角和定理:n 边形的外角和等于
对角线 :n 边形的对角线共有 条
多边形 ① 两组对边分别平行---_____
2、 四边形
② 一组对边平行且相等----略
3、其它多边形
二、判断:
1、四边形具有平行四边形所有的性质. ( )
2、平行四边形的对角线互相平分且相等. ( )
3、平行四边形既是轴对称图形又是中心对称图形.( )
4、一组对边平行,另一组对边相等的四边形是平行四边形.( )
5、一组对边平行,一组对角相等的四边形是平行四边形.( )
6、平行四边形的两条对角线把平行四边形分成四个面积相等的小三角形.( )
7、正八边形和正方形的组合能够进行密铺. ( )
三、选择:
1、 ABCD 的四个内角的度数的比∠A:∠B:∠C:∠D 可能是 ( )
A、2:5:2:5 B、3:4:4:3 C、4:4:3:2 D、2:3:5:6
2、下列图形是中心对称图形的是 ( )
A B 、 C、 D、
3、若一个多边形的每一个内角都等于 120°,则它是 ( )
A、正方形 B、正五边形 C、正六边形 D、正八边形
4、 如图,在 ABCD 中,AE 平分∠DAB,∠B=100°,则∠DEA=
( )
A、100° B、80°
C、60° D、40°
5、下列图形中,不能进行密铺的是 ( )
A、正三角形 B、正方形 C、正六边形 D、正五边形
6 、 如图,在 ABCD 中,EF 过对角线的交点 O,交 AD 于 E,
交 BC 于 F,已知 AB=4,BC=5,OE=1.5,则四边形 EFCD 的周长
是 ( )
A、14 B、12 C、16 D、10
Ⅱ 、 【尝试】
性质:包括边、角、对角线、对称性等
判定
例 1: 如图, ABCD 的对角线 AC,BD 相交于点 O,由此你能得出哪些结论?试尽可能多的写
出一些来.
分析:分别从平行四边形的边、角、对角线方面去考虑,然后思考
从这些结论出发得出的新的结论。
解:AB=CD ,AD=BC,DO=BO,AO=CO,
∠ADC=∠ABC,∠DAB=∠DCB,∠ADB=∠DBC,∠BDC=∠ABD,∠DCA=
∠CAB, ∠ACB=∠DAC
△ADO≌△CBO,△DOC≌△BOA,△ADC≌△CBA,△ADB≌△CBD,
S△DOC=S△AOD=S△AOB=S△BOC 等。
提炼:对于这种结论开放的题目,要注意思维发散,灵活运用平行四边形的性质,从不同的
角度去考虑。
例 2:图, 已知一个多边形的内角和是它的外角和的 5 倍,求这个多边形的边数。
分析:注意多边形的外角和始终是 360°
解: 设这个多边形是 n 边形,则
(n-2)×180°=5×360°,得 n=12
答:这个多边形是十二边形。
提炼:多边形的内角和与外角和既有区别,又有联系。多边形的内角和随边数的变化
而变化,而外角和是一个定值。已知内角和与外角和的关系,可以运用方程思
想解决。
例 3:如图:在 △ABC 中,D、E 分别是 AB、AC 的中点,F 是 DE 延长线上的点,且 EF=DE,则
图中的平行四边形有哪些?说说你的理由。
分析:已知条件中 AE=EC,DE=FE,不难得到四边形 ADCF 是平行四边形,
然后推出 AD∥CF,又可证到 AD=CF,所以四边形 DBCF 也是平行四边形。
解: ADCF, DBCF
理由:∵D、E 分别是 AB、AC 的中点
∴AE=EC,AD=DB,
又∵EF=DE,∴四边形 ADCF 是平行四边形(对角线互相平分的四边形是平行四边形)
∴AB∥CF,AD=CF,∴BD=CF,∴四边形 DBCF 也是平行四边形(一组对边平行且相等的四
边形是平行四边形)
提炼:运用数形结合的思想,灵活运用平行四边形的判定方法,关注由结论又可以推出新的
结论。
例 4:如图,已知 ABCD 的周长为 40,高 AE=6,高 AF=9,试根据条件设计一个问题,并进行解
答.
分析: 答案不唯一,如:已知 ABCD 的周长和边上的高,
会想到平行四边形的面积,而平行四边形的面积要涉及底和
高,所以可以设计求平行四边形的边长。
解:设计的问题可以是:求 AB、BC 的长。
因为 ABCD 的面积 S=BC*AE=CD*AF
所以 6BC=9CD,因此 BC=
2
3 CD,
又因为 ABCD 的周长为 40,所以 BC+CD=20,可解得
AB=8,BC=12
提炼:运用数形结合的思想,将已知条件和图形结合起来考虑。
Ⅲ、【小结】
3、 本节课主要内容:见唤醒中的“知识结构图”。
4、 运用数形结合的思想、方程的思想解决平行四边形中的计算和证明。
Ⅳ、【实践】
(1) 教师自行设计作业;
(2) 复习指导用书第 88--90 页第 1、4、5、7、8、10、11、13、15、16、17 题。
第 16 课时 特殊平行四边形、梯形与证明
钱惠琴
复习教学目标:
1、 能说出矩形、菱形、正方形、梯形的概念和性质,以及四边形是矩形、菱形、正方形、
等腰梯形的条件,了解它们之间的关系。知道直角三角形斜边上的中线等于斜边的一半。
2、 会根据矩形、菱形、正方形、梯形的性质和判定进行运算和推理,理解顺次连接一个四
边形的中点所构造的四边形是特殊的四边形。
3、 能运用转化思想将梯形转化为平行四边形和三角形问题解决,并能运用类比、逆向联想
及运动的思维方法来研究问题。
复习教学过程设计:
Ⅰ.【唤醒】
一、 填空:
1、 请同学们仿照图中已填写的部分将它们补充完整:
2、 对角线_____________的平行四边形是菱形。
3、 对角线_____________的四边形是矩形。
4、 直角三角形斜边上的中线等于_____________。
5、 正方形具有而矩形不具有的性质是________________ 。
6、 请写出等腰梯形 ABCD(AB∥CD)具有而一般梯形不具有的三个特征:
__________________,__________________,______________________。
7、 顺次连接矩形的四边中点所得的四边形是_____________形。
二、 判断:
1、 角线互相垂直的四边形是菱形 ( )4、腰梯形的两个底角相等 ( )
2、 个角都相等的四边形是矩形 ( )5、组对边平行的四边形是梯形 ( )
3、 角线互相垂直且相等的四边形是正方形( )
三、 选择:
1、 菱形的一个内角是 120º,一边长是 8,那么它较短的对角线长是( )
A.3 B.4 C.8 D.8
2、梯形的上底长为 6cm,过上底一个顶点引一腰的平行线,交下底所得的三角形的周长是
19 cm,那么这个梯形的周长为( )
A.31 cm B.25 cm C.19 cm D.28cm
3、若矩形一内角的平分线分长边为两部分的长分别为 2 和 3,则该矩形的面积为( )
A.6 B.10 C.15 D.10 或 15
4、如图,四边形 ABCD 是正方形,四边形 AEFC 是菱形,则∠FAB 等于( )
A.45º B.30º C.75º D.22.5º
5、下列各组图形中,既是轴对称图形,又是中心对称图形的是( )
A. 平行四边形、菱形、正方形 B.等腰梯形、矩形、正方形
C.等边三角形、矩形、圆 D.菱形、正方形、圆
Ⅱ. 【尝试】
例 1、如图,把一张矩形纸片 ABCD 沿 BD 对折,使点 C 落在 E 处,BE 与 AD 相交于 O,写出
一 组 相 等 的 线 段 ______________________________( 不 包 括
AB=CD,AD=BC)
分析:本题是开放性问题,答案不唯一,可采用两种方法:
(1) 从条件入手,根椐对称性质、全等性质、矩形的性质等,
逐步深入分析,发现需要的结论;
(2) 通过观察、比较找出可能相等的线段,再论证。
解:BE=BC 或 CD=ED 或 AB=ED 或 OB=OD 或 OA=OE 。
提炼:折叠的问题实质就是对称的问题,在折叠的问题中折痕所在的直线就是对称轴。在折
痕两侧互相重合的部分是全等的图形,从而可以得到许多相等的边、角。
例 2、 如图, ABCD 的对角线 AC 的垂直平分线与 AD、BC 分别交于 E、F,
求证:四边形 AFCE 是菱形
分析: 由于四边形 AFCE 的对角线互相垂直,那么只需证明对角线互相平
分即可,故只需证 OE=OF,而这可由证明△AOE≌△COF 得到。
证:(略)
提炼:解决此题的关键是要准确理解题意,EF 是线段 AC 的垂直平分线。另一种方法证完后
还可问学生,还有其他方法吗?注重一题多解,激活学生的思维。
例 3、如图,两个四边形中,∠ADB=∠ACB=90º,E、F 分别是 DC、AB 的中点。
(1) 观察两个图形,你发现了什么?在下面横线上简要写出你的发现
(2) 试猜想 EF 与 DC 在位置上有无特殊关系?如有,请证明;如没有,请说明理由。
分析:(1)认真审题,注意图形位置的变化;(2)由直角三角形斜边上的中线等于斜边的
一半可知,连结 FC、FD,可得 FC=1/2AB=FD,又已知 CE=DE,根据等腰三角形的三线合一可
得 EF 垂直 CD。
略解:(1)图(2)中 Rt△ACB 由图(1)中 Rt△ACB 沿 AB 翻折 180º而得到。
(2)EF 是 CD 的中垂线。理由略。
提炼:要能体会知识之间的内在联系,合理添加辅助线,化难为易。
例 4、 已知直角梯形 ABCD 中,AD∥BC,AB⊥BC,AB=6,
AD=8,∠C=45º,有一点 P 从 D 向 A 以每秒 1 个单位的
速度行动,有一点 Q 从 B 向 C 以每秒 1.5 个单位的速度
行动。问:在运动过程中四边形 PQCD 能成为特殊的四边
形吗?什么时候成为怎样特殊的四边形?
分析:由于 AD∥BC,四边形 PQCD 能否成为特殊的四边形,只需看点 P、点 Q 在运动过程中
四边形 PQCD 的对边或邻边能否相等,因此需分情况讨论并计算。
解略(当 t= 5.6 秒 时,四边形 PQCD 为平行四边形;当 t=0.8 秒时,四边形 PQCD 为等腰梯
形;当 t=3.2 秒 时,四边形 PQCD 为直角梯形。)
提炼:要注意数形结合和分类思想,同时考虑问题要全面,防止遗漏。
Ⅲ、【小结】:
1、 单元知识结构(见填空),并重点从边、角、对角线理解特殊平行四边形、梯形的
性质和判定。
2、 本课运用的数学思想方法:转化思想、类比思想、分类思想等。
Ⅳ、【实践】
1、 教师自行设计作业。
2、 复习指导用书第 92——94 页练习五、第 96——97 页练习六。
第 17 课时 圆(1)
张云娟
复习教学目标:
1、 知道圆、弧、弦、圆心角、圆周角等基本概念;认识圆的对称性;了解圆锥的侧面展
开图是扇形。
2、 能用垂径定理,圆心角、弧、弦之间关系定理,圆周角定理及推论,弧长公式等进
行简单的运算和推理;会通过作图的方法理解确定圆的条件。
3、 会用折叠、旋转、圆的对称性及分类讨论的思想方法探索图形的有关性质,能将有
关弦长、半径的实际计算问题转化成解直角三角形问题解决。
复习过程设计
一、【唤醒】
1、填空
基本概念: 弧、弦、圆心角、圆周角
确定圆的条件:
对称性:
垂径定理及逆定理
圆 基本性质: 圆心角、弧、弦的关系定理:
圆周角定理:同弧或等弧所对的圆心角是它所对的圆周角的
推论:(1)同弧或等弧所的圆周角
(2)90°的圆周角所对弦是 ,
与圆有关的计算公式 : (1) ;
(2) ;
(3) ;
(4 ) ;
2、判断:(1)圆是轴对称图形,其对称轴是任意一条直径; ( )
(2)平分弦的直径垂直于弦,并且平分弦所对的弧; ( )
(3)过任意三点可确定一个圆; ( )
(4)任何三角形只有一个外接圆,一个圆也只有一个内接三角形;( )
(5)一条弦所对的圆心角是它所对的圆周角的 2 倍。 ( )
3、选择题:
(1)⊙O 的直径为 10,圆心 O 到弦 AB 的中点 M 的长为 3,则弦 AB 的长是( )
(A)4; (B)6; (C)7; (D)8
(2)△ABC 内接于⊙O,AB=AC,∠A=50°,D 是⊙O 上一点,则∠ADB 的度数
为( )
(A)50° ; (B)65° ;(C)65°或 50° ; (D)115°
或 65°
(3)如图所示,⊙A、⊙B、⊙C、⊙D、⊙E 相互外离,它们的半径都是 1,顺次连
接五个圆心,得到五边形 ABCDE,则图中五个扇形(阴影部分)的面积之和
是( )
(A)∏; (B)1.5∏ ; (C)2∏ ; (D)2.5∏
(4)如果圆锥的侧面展开图的面积是 15∏cm 2, 母线长是 5cm,那么圆锥的底面半径
为( )
(A)3cm; (B)1.5cm; (C)6 cm; (D)4 cm
(5)已知△ABC 是半径为 2 的圆内接三角形,若 BC=2 3 ,则∠A 的度数为( )
(A)30°; (B)60°; (C)120°; (D)60°或 120°
(6)图中的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从
A 点到 B 点甲虫沿弧 ADA1、弧 A1EA2、弧 A2FA3、弧 A3GB 的路线爬行,乙虫沿
弧 ACB 的路线爬行,则下列结论正确的是( )
(A)甲虫先到 B 点; (B)乙虫先到 B 点;
(C)甲虫、乙虫同时到达 B 点;(D)无法确定。
二、【尝试】
例 1、如图,在△ABC 中, ∠BAC 的平分线 AD 交△ABC 的外接圆⊙O
于点 D,交 BC 于点 G,若 AG=6,DG=2,求 CD 的长。
分析:连接 DC,用相似三角形解决。
解略。(DC=4)
例 2、 ABC 中,AB=AC=10,BC=12,求△ABC 外接圆的半径。
分析:利用三角形外心的特殊位位置和垂径定理构造直角三角形解决。
解略。( △ABC 外接圆的半径为 6.25 )。
提炼:善于用数学转化的思想方法,将不同情境下的数学问题转化为比
较熟悉的直角三角形问题解决。
例 3、 1)如图,小军学完垂径定理,逆向思考得出一个结论:“弦的垂直平
分线一定经过圆心,并且平分弦所对的两条弧”,你认为小军的猜测
正确吗?为什么?
(2)你能用上面的结论,帮助考古学家用尺规作图的方法确定古圆盘
的半径吗?
分析:(1)根据圆上的点到圆心的距离相等进行说理
(2)圆心可有两条不同的直径相交确定,因此要确定圆心,只要确
定出两条不同的直径就可,由两条不同的弦,作其垂直平分线,
则 交点就是圆心。
解:(1)∵圆心 O 到 A 和 B 的距离相等,
∴点 O 一定在 AB 中垂线上。
即 AB 的中垂线过圆心。
(2)略
提炼:能将学圆性质时的探究方法灵活运用到探索新的有关结论,并能应用。
例 4、 ※如图:把直角三角形 ABC 的斜边 AB 放在直线 l 上,按顺时针方向在
l 上转动两次,使它转到△A2B2C2 的位置,设 BC=1,AC= 3 ,则点 A
运动到点 A2 的位置时,点 A 经过的路线长是多少?点 A 经过的路线与
直线 l 所围成的面积是多少?
分析:点 A 经过的路线长就是以 B 为圆心,以 AB
为半径的圆弧和以 C2 为圆心,以 AC 为半径的圆
弧的长度。面积就是两个扇形面积与一个直角三角
形的面积和。
解:点 A 经过的路线长为
6
338 π; 点 A 经过的路线与直线 l 所围成的面积
是
12
25 π+
2
3
提炼:在理解旋转性质的基础上将问题转化为所学的有关圆的计算公式解决。
三、【小结】1、知识结构:见上表
2、基本数学思想方法:转化的思想;分类讨论的思想;数形结合的思想等。
3、解题注意点:(1)在解决问题的过程中,注意归纳总结出解决问题的一些基本规律,
提高学习效率;(2)注意解决问题的严密性,充分考虑各种情况。
四、【实践】教师自行设计作业;复习指导用书第 107~109 页第 1、2、5、6、9、12、
21 题。
第 18 课时 圆(2)
张云娟
复习教学目标:
4、知道圆与点、圆与直线、圆与圆的不同位置关系;知道切线的概念。
5、会用圆心到点的距离大小判断圆与点的位置情况,圆心到直线的距离大小判断圆与点直
线的位置情况;圆心到圆心的距离大小判断圆与圆的位置情况;会用圆的切线的判定定理
和性质定理及两圆相切的性质与判定进行简单的推理与计算;会作三角形的外接圆、内切
圆,会过圆上点作圆的切线。
6、能从运动的观点与分类讨论的思想方法探索图形之间的关系和有关性质。
复习过程设计
一、【唤醒】
1、 填空 (1)点在圆外 点到圆心的距离 d > r
圆与点的位置关系: (2) 点到圆心的距离 d r
(3) 点到圆心的距离 d r
(1)相离 圆心到直线的距离 d > r
圆与直线的位置关系 (2) 圆心到直线的距离 d r
圆
(3) 圆心到直线的距离 d
r
(1)相离
圆与圆的位置关系:
(2)相交
(3)相切
2、判断:(1)若圆经过 A、B 两点,则圆心一定可能是线段 AB 的中点; ( )
(2)若直线与圆有公共点,则直线与圆相交; ( )
(3)圆的切线垂直于圆的直径; ( )
(4)垂直于直径的直线是圆的切线; ( )
(5)垂直于圆的切线的直线一定过切点; ( )
(6)若两圆无公共点,则这两圆外离; ( )
(7)直线 l 上一点 P 到圆心 O 的距离等于半径 R,则直线 l 与圆 O 相切。( )
3、选择题:
(1)A、B 两点到点 O 的距离等于 4cm ,则点 A、B 在( )
(A)⊙O 上; (B)⊙O 内; (C)⊙O 外; (D)无法确定。
(2)如图所示:已知等边△ABC 的边长为 2 3 cm,下列以 A 为圆心的各圆中,半径是
3cm 的圆是( )
(A) ;(B) ; (C) ;(D)
(3)点 P 到△ABC 各边的距离相等,则点 P 是△ABC 的( )
(A)内心; (B)1.外心 ; (C)中心 ; (D)垂心。
(4) 已知△ABC 的三边分别是 6、8、10,则此三角形外接圆的半径为( )
(A)10; (B)6; (C)4; (D)5
(5)两个同心圆,大圆的弦 AB 与小圆相交于点 C、D 两点,若 AB=6,CD=2,则两圆组成
的圆环面积是( )
(A)32π (B)16π (C)8π; (D)无法确定
二、【尝试】
例 1、已知 Rt△ABC 的斜边 AB=13,AC=5,CD 是 AB 边上的高。(1)以 C 为圆
心,当半径为多少时,AB 与 ⊙C 相切?(2)此时⊙C 与点 A、B、C、D 之间是怎
样的位置关系?
分析:判断点与圆的位置关系关键是利用圆心到点的距离与半径的大小关系;判断直线
与圆的位置关系关键是利用圆心到直线的距离与半径的大小关系,而不是直线上任意一点
到圆心的距离。
解略。(答案:R=60/13;点 A、B 在圆外,点 D 在圆上,点 C 在圆内。)
提炼:让学生通过具体问题的解决进一步体会分类思想是研究图形的一种。 重要的数学
方法。
例 2、已知,如图 AB=8,AC=6,以 AC 和 BC 为直径作半圆,过 AB 的延长线上一点 D 作
直线,分别与⊙O1 和⊙O2 相切于点 M、N,求 BD 的长。
分析:正确理解圆的切线的性质定理,由切线想
过切点作半径,可得到垂线段,然后利用三
角形相似求得线段 BD 的长。
解略。(答案:BD=1)
提炼:能利用方程的思想,根据切线的性质结合
相似三角形的知识,通过设未知数列方程
加以计算。
例 3、读句画图:⊙O 和任意一点 P,连接 OP,以 OP 为直径作⊙Q。
(1)、在所画的图形中,⊙O 与⊙Q 有怎样的位置关系?
(2)、当⊙O 与⊙Q 相交时,交点为 A、B,分别作直线 PA 与 PB,则 PA、PB 与⊙O 是
什么位置关系?并说明理由。
(3)、在题(2)下,连接 AB、OA、OB,请根据所画图形尽可能多地写出你认为正确的
结论。
分析:①画图时要能想到点 P 与⊙O 的不同位置,从而⊙O 与⊙Q 也就有不同的位置情况。
②利用切线的判别定理说明直线与圆的位置关系。③正确画图的基础上,寻找线段之间、三
角形之间的数量与位置关系。
解:①两圆有内切、相交、内含这三种位置关系;②直线 PA 与 PB 是⊙O 的切线;③在
一般情况下,线段 OQ 垂直平分 AB,在特殊情况下,除了具有一般情况下的结论,线段
OQ 与 AB 互相垂直平分。
提炼:在画图时通常需要分类讨论,并且用特殊到一般的思想方法解决具体问题
三、【小结】
1、知识结构:见上表
2、基本数学思想方法:转化的思想;分类讨论的思想;由特殊到一般的思想等。
3、解题注意点:在解决问题的过程中,注意解决问题的严密性,充分考虑各种情况。
四、【实践】(1)教师自行设计作业;(2)复习指导用书第 107~109 页第 3、4、16、
18、22 题。
第 19 课时 作(画)图
朱淑芳
复习教学目标:
1、 能用三角板或量角器过一点画已知直线的垂线, 能用三角板、直尺过直线外一点作已知
直线的平行线;能用直尺和圆规作一条线段等于已知线段、作一个角等于已知角;作角
的平分线;作线段的垂直平分线。了解尺规作图的步骤,对于尺规作图题会写已知、求
作和作法(不写证明);
2、 会用三角板作三角形的高,会用直尺和圆规利用已知条件作一个三角形;会过一点、两
点和不在一条直线上的三点作圆;
3、 把一些较复杂的作图问题转化为基本作图问题来解决。
复习教学过程设计:
一、【唤醒】
1、 填空:
(1)尺规作图的基本工具是 和 。
作一条线段等于已知线段
作一个角等于已知角
(2)(阅读)基本作图 : 作一个角的角平分线
作一条线段的垂直平分线
已知三边作三角形
已知两边及夹角作三角形
(3)(阅读)利用基本作图作图 已知两角及其夹边作三角形
已知底边及底边上的高作等腰三角形
过一点、两点和不在一条直线上的三点作圆。
2、 判断:
(1)画一条直线 a,使 a=10cm。 ( )
(2)过点 A 作线段 BC 的中垂线。 ( )
(3)过三点 A、B、C 一定能画一个圆。 ( )
(4)过一点一定能作一条已知直线的垂线。 ( )
3、 选择:
(1)三角形的外心是 ( )
A、 三条高的交点 B、三条中线的交点
C、三条角平分线的交点 D、三边垂直平分线的交点
(2)到 B、C 两点的距离相等的点有 ( )
A、一个 B、两个 C、无限个 D、有限个
(3)下列所给条件不能确定一个圆的是 ( )
A、圆心及圆经过的一点 B、圆心及半径 C、圆经过的两点 D、一段圆弧
二、【尝试】
例 1 利用尺规,按下列要求作图,不写作法,保留作图痕迹。
(1) 作出 AB 的中点 M;
(2) 作∠BCD 的平分线;
(3) 延长 CD 到 P,使 DP=2CD。
分析:本题考查学生用尺规进行基本作图
解:(略)
提炼:本题同时考查了尺规作垂直平分线、作角平分线、作一条线段等于已知线段等知
识。
例 2 小明的爸爸上街配一块三角形的玻璃,到街上后发现把所量的三边长度弄丢了,打电
话问小明,小明却回答他:两边长为 30cm 和 50cm,这两边的夹角为 45 。请问:按
照这三个数据,他爸爸能配到符合要求的玻璃吗?若能,请按 1:10 的比例画出这个
三角形;若不能,请说明理由。
分析:根据“两边及夹角对应相等的三角形全等”,所以能配到符合要求的玻璃。
解:(略)
提炼:这题一方面考查了三角形全等的判定,另一方面帮学生复习 1:10 作图的含义。
例 3 已知 Rt△ABC 中,∠C= 090 ,用直尺和圆规作图,把它分成两个直角三
角形,且要求其中至少一个三角形为等腰三角形(至少两种方法)
分析:本题关键是根据等腰三角形的定义想办法得到相等的线段
解:(略)
提炼:本
题是开放题,考查基本作图方法及一些知识的综合运用。
例 4 两条公路 a、b 相交于点 O,A、B 为两个收购站,请在这块地上找一个仓库 P,使仓库
到两个收购站的距离相等。
分析:到两点 A、B 的距离相等的点在线段 AB 的垂直平分线上,到两边
的距离相等的点在交角的平分线上,所以求交点即可。
解:(略)
提炼:本题通过分析题意,运用作垂直平分线和作角平分线找交点,体现数学与生活的联系。
三、【小结】
前面填空部分,并能用所学综合知识解决实际问题。
四、【实践】
1、 教师自行设计;
2、 复习指导:P112:3、5、6
第 20 课时 视 图
王 飞 浦春萍
复习教学目标:
1、 认识点、线、面,会说出它们之间的关系;认识圆柱、圆锥、棱柱、球,会结合点线面
说出它们的特征;知道圆柱、圆锥的侧面展开图、正方体的侧面展开图,认识正方体、
圆柱、圆锥的截面形状,知道物体的三种视图;认识多边形。
2、 会识别简单物体的三视图,会根据三种视图描述基本几何体或实物原型;会画立方体极
其简单组合体、圆柱、圆锥、球、直三棱柱、直四棱柱的三种视图。
3、 能由实物形状想象出几何图形,由几何图形想象出实物形状,进行几何体与其三视图、
展开图之间的相互转化。
复习教学过程设计: (阅读)生活中的立体图形
一、【唤醒】
1、填空:
(1)
*在画视图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线。
(2)点动成 ,线动成 ,面动成 。
(3)四棱柱(或 n 棱柱)有 棱, 个顶点, 个面,这些面的形状都是 。
(4)圆柱的侧面展开图是 ,截面可能是 ;
圆锥的侧面展开图是 ,截面可能是 。
(5) 写出三视图中有一个是三角形的两个几何体: 。
2、判断:
(1)如图,正三棱柱的主视图、左视图、俯视图分别是: ( )
( 2 ) 一 空 间 几 何 体 的 三 视 图 如 图 所 示 , 则 这 个 几 何 体 是 圆 柱 。
( )
( 3 ) 如 图 , 截 一 个 正 方 体 得 到 的 截 面 形 状 是 平 行 四 边 形 。
( )
3、选择:
( 1 ) 图 中 几 何 体 的 左 视 图 是
( )
( 2 ) 在 下 图 中 , 平 面 图 形 经 过 折 叠 不 能 围 成 正 方 体 的 是
( )
(3)如果从一个多边形的某个顶点出发,与其余不相邻的各个顶点连接,能得到
2002 个 三 角 形 , 那 么 这 个 多 边 形 的 边 数 为
( )
A、2001 B、2002 C、2003 D、2004
( 4 ) 俯 视 图 是 的 几 何 体 是
( )
(5)将下图所示放置的 Rt△ABC(∠C=90)绕斜边 AB 旋转一周所得到的几何体
的 主 视 图 是 下 面 四 个 图 形 中 的
( )
(6)如图所示的玩具是由两个正方体用胶水黏合而成的,它们的棱长分别为 1 分
米和 2 分米。为了美观,现在其表面喷涂油漆,已知喷涂 1 平方分米需用油漆
5 克 , 那 么 喷 涂 这 个 玩 具 共 需 油 漆
( )
A、120 克 B、130 克 C、140 克 D、150 克
(7)小丽制作了一个如图所示的正方体礼品盒,那么这个正方体的平面展开图可能是
( )
(8)图示是由一些相同的小正方体构成的立体图形的三视图,构成这个立体图形的小
正 方 体 的 个 数 是
( )
A、5 B、6 C、7 D、8
二、【尝试】
例 1 画出下列几何体的三种视图。
答案:
例 2 如图的几何体是在正方体的中心挖去一个圆柱得到的,试画出该几何体的三视图。
分析:这是一个正方体和圆柱的简单结合体,可先分别考虑它们的三视图,
而后结合该几何体的特征思考它三视图中实线、虚线的画法。
答案:
例 3 下图的四边形是一个四棱柱的俯视图,尝试画出它的主视图和左视图。
分析:根据棱柱的定义,该几何体的侧面形状都是长方形,可以由其俯视图
想象出几何体形状,再思考其三视图的画法,并注意画三视图的相关
要求。
答案:
提炼:以上三题都考查了学生对几何体与其三视图之间的相互转化能力。
例 4 用若干个小立方块搭成一个几何体,它的主视图和俯视图如图所示:
(1)俯视图上标注 A、B 的各由几个小立方块搭成?
(2)搭成符合上述要求的几何体,至少需要多少个立方块?最多需要多少个立方块?
(3)这样的几何体共有几种?画出两种不同的左视图。
分析:由主视图易知,A、B 上各由 3 个、1 个小立方块搭成,关键分析中间一列的小立方
块数,每个位置上最多 2 个,最少 1 个立方块且至少有一个位置上有 2 个小立方块,
分情况讨论后,这样的几何体共计有 4 种。
答案:(1)3 个,1 个; ① ② ③ ④
(2)至少 8 个,至多 10 个;
(3)4 种。左视图:
提炼:该题实现了“视图—几何体—视图”的转化过程,可列举各种情况后再得到各种左视
图。
三、【小结】
1、见前面知识结构图;
2、由实物形状想象出几何图形,由几何图形想象出实物形状,进行几何体与其三视图、展
开图之间的相互转化。
四、【实践】1、教师自行设计作业;2、复习指导用书第 122 页第 1~5、7、8、10、11 题。
第 21 课时 投影
钱惠琴
复习教学目标:
1、通过实例了解平行投影和中心投影的含义,了解视点、视线和盲区的含义。
2、会确定物体在太阳光和灯光下的影子,初步进行平行投影和中心投影条件下物体与其投
影之间的相互转化。能体会视点、视线和盲区在生活中的应用,并能在简单的平面图和立体
图中表示。
3、能根据在太阳光下同一时刻物体与影长成正比或相似三角形来帮助我们解决一些实际问
题,会用“数学的眼光”看世界,体会数学与现实生活的联系。
复习教学过程设计:
Ⅰ.【唤醒】
一、填空
1、物体在光线的照射下,会在地面或墙壁上留下它的 ,这就是投影现象。
2、太阳光线可以看成 光线,像这样的光线所形成的投影称为 ;探照灯、
手电筒、路灯等的光线可以看成是从 点发出的,像这样的光线所形成的投影称
为 。
3 、 请 你 各 举 一 个 平 行 投 影 和 中 心 投 影 的 实
例: 。
4、当人观察物体时,眼睛的位置称为 ,由视点发出的线称为 ,看不到的地方
称为 。
5、从远处走近一个物体,我们会感觉这个物体越来越大,这是因为 。
二、判断:
1、你见过的皮影或自己用手势做的手影都是在太阳光照射下形成的中心投影。 ( )
2、两人在太阳光下行走,同一时刻他们的身高与其影长的比相等。 ( )
3、如果一根木杆在太阳光下的影长等于木杆的长,那么这根木杆与地面平行。 ( )
4、较大的会场都成阶梯形状是为了缩小各座位的盲区。 ( )
5、物体的主视图实际上就是该物体在某一时刻某一光线下的投影。 ( )
三、选择:
1、在同一时刻,物高与影长成正比例,如果高为 1.5 米的测竿的影长为 2.5 米,那么影长为
30 米的旗杆的高是 ( )
A.20 米 B.18 米 C .16 米 D.15 米
2、已知下面的四幅图是小红某天四个时刻看到的一根木棒及其影子的情况,那么她看到的
先后顺序是 ( )
(1) (2) (3) (4)
A.(1)(2)(3)(4) B.(2)(1)(3)(4) C.(4)(3)(1)(2) D.(4)
(1)(3)(2)
3、如图,晚上小亮在路灯下散步,小亮由 A 处走到
B 处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
4、兄弟两人在家中向窗外观察,图中虚线表示视线,则( ) (
A.哥哥的盲区大 B.弟弟的盲区大
C.两人的盲区一样大 D.盲区大小不确定
5、乘车沿着平坦大道向前行驶时发现前方高一些的建筑物“沉”到位于它们前面的矮一些
建筑物后面,这是由于( )
A.汽车一定在上坡 B. 汽车一定在下坡 C. 矮建筑物的盲区越来越大 D. 矮建筑物越
来越大
Ⅱ. 【尝试】
例 1、 如图(1)是两根垂直于地面的旗杆,粗线段表示旗杆甲在太阳光照射下的影子,请
你再画出: (1)太阳光线;(2)旗杆乙的影子;
如图(2)是树和旗杆及它们在灯光下的影子,试确定路灯的位置及小明在路灯下的影子。
(2)
分析:(1)已知旗杆甲和影子,可确定一条光线,即为太阳能光线,根据同一时刻太阳光
线是平行的,便可画出旗杆乙的影子;(2)根据旗杆和影子,树和影子可确定两条光线,
它们的交点就是灯的位置。
画图(略)
提炼:确定一条光线,需要两个点;确定光源的位置,需要两条光线。
例 2、 如图,小灵要到不熟悉地形的某市的新华书店去购书。
当他走到大街 A 处的位置,就断定新华书店不在附近。
你说小灵的判断正确吗?为什么?
分析:根据盲区的含义画出图形加以判断。
解:不正确。新华书店在小灵的盲区内,再往十字路口方向前走若
干米即可见。
提炼:会利用盲区的含义用“数学的眼光”看世界,体会数学与现实生活的联系。
例 3、 赵亮同学想利用影长测量学校旗杆的高度。如图,他
在某一时刻立 1 米长的标杆,测得其影长为 1.2 米,同时旗杆的
投影一部分在地面上,另一部分在某一建筑物的墙上,分别测得
其长度为 9.6 米和 2 米,求旗杆的高度。
分析: 本题难点在于影子落在了两个面上,解决此问题关键是理解当投影面与物体平行时,
影长等于其高度。然后再利用在同一时刻影长与物高成比例,或三角形相似来解。
解:延长光线 AB,与地面交于 C,墙上的投影可以看成是竖起的标杆。由已知,得 BD:
CD=1:1.2,求得 CD=2.4,CE=9.6+2.4=12。又由 AE:CE=1:1.2,解得 AE=10 米。
提炼:利用在同一时刻影子长度与物体的高度成比例解题,关键是如何理解投影在墙上的影
子,不能简单的用地面影子加上墙上影子作为旗杆的投影。
例 4、已知:CD 为一幢 3 米高的温室,其南面窗户的底框 G 距地面 1 米,CD 在地面上留
下的最大影长 CF 为 2 米,现欲在距 C 点 5 米的正南方 A 点处建一幢 9 米高的楼房 AB(设
A、C、F 在同一水平线上)
(1) 按比例较精确地作出高楼 AB 及它的最大影长 AE;
(2) 问:若大楼 AB 建成后是否影响 CD 的采光,试说明理由。
分析:由 CD=3 米,按比例易作出 9 米高的楼房 AB;根据物体都
取最大影长时太阳光线平行,作出楼房 AB 的最大影长,并利用
太阳光下同一时刻物高与影长成比例,及当物体与投影平面平行时
物高与影长相等,求出 AB-CG 的影长并与 AC 比较大小即可。
解(1)画图略;
(2)大楼 AB 建成后影响 CD 的采光。理由略。
提炼:会利用太阳光下同一时刻物高与影长成比例,及当物体与投影平面平行时物高与影长
相等来解决问题。
Ⅲ、【小结】:
1、 本单元知识结构(见填空)
2、 解题注意点:在太阳光下同一时刻物高与影长成比例,但灯光下不一定成比例。
Ⅳ、【实践】教师自行设计作业;复习指导用书第 123—124 页练习二第 6、9、12、13、14
题。
第 22 课时 图形的变换
张旗
复习教学目标:
1、了解轴对称、平移、旋转这三种图形变化的主要特征和基本性质。
2、会判断常见图形的对称性,探索图形之间的变换关系。
3、会利用轴对称、平移、旋转的组合进行图案设计。
复习教学过程设计
一、【唤醒】
1、 填空:
(1)
变换类型 要求 性质 研究变换图形的关键
翻折 沿一条直线翻折______
翻折后所得图形与原图形关于
这条直线成 对称。对应点
所连的线段被对称轴________。
找对应点
找对应边
找对应角
找对应图形
平移 需要知道原来的位置及平
移的 和
平移不改变图形的 和 ____
对应点的连线____且____。
旋转
需要知道原来的位置和旋
转中心外,还要知道旋转的
方向及旋转角度。
对应点到旋转中心距离 对应
点的旋转中心的连线所成的角
彼此 。
(2)如图所示,∠AOB=∠COD=60°,OA=OB,OC=OD,把△AOC 绕着点 O 旋转 60°,点 A
将落在点_____上,点 C 将落在点_____上,因此,△AOC 与△BOD 可以通过______变换完
全重合。
B C (1) (2) (3)
A O D
第(2)题 第(3)题
(3)如图,由小正方形组成的 L 形图中,请你用三种方法分别在上图中添画一个小正方形
使它成为轴对称图形。
2、 判断:
(1) 旋 转 变 换 前 后 的 图 形 中 , 对 应 线 段 平 行 且 相 等 , 对 应 角 相 等 。
( )
(2) 关 于 某 直 线 对 称 的 两 个 图 形 , 对 应 角 相 等 , 对 应 点 连 线 平 行 且 相 等 。
( )
(3) 平 移 后 的 图 形 与 原 来 的 图 形 的 对 应 线 段 平 行 且 相 等 。
( )
3、 选择题:
(1)如果△ABC 和△A1B1C1 成中心对称,△A1B1C1 和△A2B2C2 成轴对称,则△ABC 和△
A2B2C2 有( )
A.全等关系 B.无全等关系 C.可能有全等关系 D.以上都不对
( 2 ) 矩 形 ABCD 和 A1B1C1D1 于 点 A 成 中 心 对 称 , 则 四 边 形 BDB1D1 是
( )
A.矩形 B.菱形 C.正方形 D.梯形
(3)如图,有一块直角三角形纸片,两直角边 AC=6cm,BC=8cm,现将
直角边 AC 沿直线 AD 折叠,使它落在斜边 AB 上,且与 AE 重合,则 CD
等于( )
A.2cm B.3cm C.4cm D.5cm
A
E
C D B
二、【尝试】
例 1、 在下面的网格中按要求画出图形,要求:先画出△ABC 向下平移 5 格后的△A1B1C1,
再画出
△ABC 以点 O 为旋转中心,沿顺时针方向旋转 90°后的△
A2B2C2。
例 2 图
例 2、 已知:如图: ABCD
(1)画出 A1B1C1D1,使 A1B1C1D1 与 ABCD 关于直线 MN 对称;
(2)画出 A2B2C2D2,使与 ABCD 关于点 O 中心对称;
(3) A1B1C1D1 与 A2B2C2D2 是对称图形吗?若是,请在图上画出对称轴或对称中心。
提炼:由例 1 和例 2 可知,画变换图形应抓住对应点,先画点,再连线。
例 3、如图:线段 AB 绕点 O 旋转了一个角度后成为线段 CD,由于不小心点
O 被擦掉,你能找到点 O 的位置吗?
分析:由于对应点到旋转中心的距离相等,即 AO=CO,BO=DO,因此
点 O 既在线段 AC 的垂直平分线上,又在线段 BD 的垂直平分线上,帮点 O
在两垂直平分线的交点上。解答见《复习指导》P116。
提炼:对应点连线的中垂线过旋转中心。
例 4,(1)操作与证明:如图,O 是边长为 a 的正方形 ABCD 的中心,将一块半径足够长,
圆心角为直角的扇形纸板的圆心放在 O 点处,并将纸板绕 O 点旋转。求证:正方形 ABCD
的边被纸板覆盖部分的总长度为定值 a。
(2)尝试与思考:如图,将一块半径足够长的扇形纸板的圆心放在边长为 a 的正三角形或
边长为 a 的正五边形的中心 O 点处,并将纸板绕 O 点旋转。当扇形纸板的圆心角为 时,
正三角形的边被纸板覆盖部分的总长度为定值 a;当扇形纸板的圆心角为 时,正五边
形的边被纸板覆盖部分的总长度也为定值 a。(正多边形的中心即正多边形各边垂直平分线的
交点.)
分析:本题为实验型探究题,解题的关键在于理解题意,按
题意动手操作,在动手操作中获得知识,接着把正方形推广到正三角
A
C
B
O
例 1 图
OO
A D
CB
N
A
CB
O
B
A
E
DC
O
A
B
C
D
A
D
C
B
M
N
O
形和正五边形。进而引申到任意正多边形中去,体现了从特殊到一般
研究数学问题的方法,有效地考查了学生动手、观察、猜想、归纳、
探究的能力。
解:(1)略 (2)120°, 72°
提炼:旋转图形时应抓住旋转角,同时引导学生观察猜想。
三、【小结】
1、 知识点见前表
2、 在翻折、平移、旋转图形的思考中,应抓住对应的点,对应的角和对应的线段研究问题。
四、【实践】
(1) 教师自行设计作业
(2) 《复习指导用书》第 116-120 页第 1、2、4、5、7、9、10、11、17。
第 23 课时 相似形(1)
芮和保
复习教学目标:
1、 知道线段的比、比例线段、黄金分割、相似、位似等概念,了解比例的性质。
2、 会利用比例的性质进行比例变形,会用相似多边形的性质解决实际问题,能够利用位似
将一个图形放大或缩小。
3、体会利用从特殊到一般解决问题的方法和分类的数学思想
复习教学过程设计:
一、【唤醒】
1、填空:
(1)比例线段
(2)比例性质
(3) 黄金分割:若点 C 是线段 AB 的黄金分割点(AC>BC),则 AC:AB=_____
(4) 位似图形的性质:位似图形 上任意一对对应点到位似中心的距离等于
__________
2、判断:
( 1 ) 、 由 a ∶ b=7 ∶ 9 得 7a=9b
( )
( 2 ) 、 有 一 个 角 对 应 相 等 的 菱 形 相 似
( )
(3)、如果四边形 ABCD 和四边形 A1B1C1D1 是位似图形,且位似比为 k,那么
1 1 1
S ACD
S A C D
= 2
1
k
( )
( 4 ) 、 位 似 图 形 一 定 是 相 似 图 形 , 相 似 图 形 也 一 定 是 位 似 图 形
( )
3、选择:
1、______________________________
2、______________________________
3、______________________________
⑴、A、B 两地实际距离 AB=250m,画在图上的距离 A/ B/=5cm,则这幅图的比例尺是----------
( )
A、1∶50 B、50∶1 C、1∶5000 D、1∶500
⑵、已知 a、b、c、d 是成比例线段,且 a=4,b=3,c=8,则 d 等于------------------------( )
A、 3 2
3
B、 3
2 C、5 D、6
⑶ 、已知 a c
b d
,下列变形错误的是--------------------------------------------------------------------
( )
A、 a c c
b d d
(b+d≠0) B、 ( 0)ax c xbx d
C、 a b c d
b d
D、 1 1a c
b d
⑷、已知 2 ( 0)3
m p n qn q
,则 m p
n q
----------------------------------------------------------
( )
A、 4
3 B、 2
3 C、 1
3 D、2
⑸、两个相似多边形的相似比为 2∶3,周长之和为 65cm,则较大的多边形周长为--------
( )
A、39cm B、45cm C、 130
3
cm D、 260
9
cm
⑹、若点 C、D 是线段 AB 的黄金分割点,且 AB=1,则 CD=-----------------------------------------
( )
A、 5 1
2
B、 5 1
2
C、 5 2 D、 5 3
二、【尝试】:
例 1、已知三条线段长度分别为 4、8、5,试写出另一条线段,使这四条线段为成比例线段。
分析:这是一道开放题,目的在于考查学生对比例线段概念的理解,题中没有明确告诉具体
的比例式,所以本题包含着多种情况。
解略,答案: 32
5
、 5
2
、10
提炼:认真审题,正确应用分类思想,防止漏解。
例 2、一木框的内外是两个矩形 ABCD 和 EFGH,按图中尺寸,在什么条件下两个矩形相似?
分析:这是一道结合比例性质和多边形相似判定的题目,解答本题时,要根据多边形的定义,
看题中还缺少判定四边形相似的什么条件,从要找的条件入手列出比例式,再根据比例的性
质进行变形。
解:由题意得:要使两个矩形相似,还须 2
2
m m b
n n a
由比例的基本性质得: 2 ( 2 )
2 ( 2 )
m m b m m b b
n n a n n a a
n
m
b b
a
aE H
GF
C
D
B
A
即当 m b
n a 时,两个矩形相似。
提炼:当 a=b 时两个矩形相似,但这只是其中的一种特殊情况。本题属于条件探索题,解题
时不要把条件和结论用错了。
例 3、 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
探究:(1)如图甲,已知△ABC 中∠C=900,你能把△ABC 分割成 4 个与它自己相似
的小直角
三角形吗?若能,请在图甲中画出分割线,并说明理由.
(2)一般地,“任意三角形都是自相似图形”,只要顺次连结三角形各边中点,则可
将原三角形分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各
边中点所进行的分割,称为 1 阶分割(如图 1);把 1 阶分割得出的 4 个三角形再分别顺次
连结它的各边中点所进行的分割,称为 2 阶分割(如图 2)…依次规则操作下去.n 阶分割后
得到的每一个小三角形都是全等三角形(n 为正整数),设此时小三角形的面积为 SN,若△
DEF 的面积为 10000,利用计算器探索当 n 为何值时,2= 750) {
docEl.style.fontSize = '100px';
} else {
docEl.style.fontSize = 100 * (clientWidth / 750) + 'px';
}
};
if (!doc.addEventListener) {
return;
}
win.addEventListener(resizeEvt, recalc, false);
doc.addEventListener('DOMContentLoaded', recalc, false);
})(document, window);
var detail_sidebar = {
init: function(){
var that = this;
that.top();
that.next();
},
top: function(){
var $top = $('#sidebar ul.list li.top');
$(window).scroll(function() {
clearInterval(d);
var d = setTimeout(function(){
if($(window).scrollTop() >= 100){
$top.fadeIn(300);
}else{
$top.fadeOut(300);
}
},300)
});
$top.find('a').on('click',function(){
$('html,body').animate({
scrollTop: '0px'
}, 1000);
});
},
next: function(){
$('#sidebar ul.list li.next a').on('click',function(){
operate_next.init();
});
}
};
detail_sidebar.init();
var previewMoreCon = {
encodeHasLeftView: true, //转码-是否还有剩余预览未显示
encodePage: 0, //转码-剩余预览页码
encodeLeftImgList: [], //转码-待加载图片列表
encodeSuffix: '', //转码-预览图片前缀
encodeMoreBtn: '#encodeMoreBtn', //转码-预览更多图片触发按钮
encodeMoreCon: '#encodeMoreCon', //转码-图片容器
noEncodeHeight: 800, //未转码-超出高度
noEncodeCon: '#noEncodeCon', //未转码-文本容器
noEncodeMroeBtn: '#noEncodeMoreBtn', //未转码-预览更多图片触发按钮
isEncode: true, //是否转码
init: function(moreCallback, noMoreCallback){
var _this = this;
var encodeMoreBtn = this.encodeMoreBtn.slice(1);
if (document.getElementById(encodeMoreBtn) && $(this.encodeMoreBtn).is(':visible')) {
this.isEncode = true;
this.getImgList();
$(this.encodeMoreBtn).click(function () {
_this.loadMoreImg($(this),moreCallback, noMoreCallback)
})
} else {
this.isEncode = false;
//未转码页面显示更多
if ($(this.noEncodeCon + ' .detail-con-more-txt').outerHeight(true) > this.noEncodeHeight) {
$(this.noEncodeMroeBtn).show();
} else {
$(this.noEncodeMroeBtn).hide();
}
$(this.noEncodeMroeBtn).click(function () {
//如果未登录则弹出登录框
// if (!LOGIN_STATUS || LOGIN_STATUS === '') {
// messageAlert.bsError('获取登录状态中,请稍后重试');
// return;
// } else if (!LOGIN_STATUS || LOGIN_STATUS !== '1') {
// $('#loginModal').modal('show');
// return;
// }
$(this).prop('disabled', true).addClass('text-primary').text('全部内容已经预览完成,下载至电脑可进行编辑');
$(_this.noEncodeCon).removeClass('detail-con-more')
});
}
},
getImgList: function() {
var _this = this;
var imgListItemSrcArr = $(this.encodeMoreCon + ' img:last').attr('src').split('/');
var imgListItemSrcNum = parseInt(imgListItemSrcArr[imgListItemSrcArr.length - 1].split('.')[0]);
var imgListItemSrcSuffix = '.' + imgListItemSrcArr[imgListItemSrcArr.length - 1].split('.')[1];
var leftImgNum = $(this.encodeMoreBtn + ' b').text();
leftImgNum = leftImgNum ? parseInt(leftImgNum) : 0;
imgListItemSrcArr.pop();
var imgListItemUrl = imgListItemSrcArr.join('/');
for (var i = 0; i < leftImgNum; i++) {
var imgUrl = imgListItemUrl + '/' + (imgListItemSrcNum + i + 1) + imgListItemSrcSuffix;
_this.encodeLeftImgList.push(imgUrl);
}
},
loadMoreImg: function(btn, moreCallback, noMroeCallback){
var _this = this;
//如果未登录则弹出登录框
// if (!LOGIN_STATUS || LOGIN_STATUS === '') {
// messageAlert.bsError('获取登录状态中,请稍后重试');
// return;
// } else if (!LOGIN_STATUS || LOGIN_STATUS !== '1') {
// $('#loginModal').modal('show');
// return;
// }
//如果没有剩余预览未显示
if (!this.encodeHasLeftView) {
return;
}
this.encodePage++;
var minNum = (this.encodePage - 1) * 5 - 1;
var maxNum = this.encodePage * 5;
$(this.encodeLeftImgList).each(function (index, item) {
if (index > minNum && index < maxNum) {
var img = document.createElement('img');
img.src = item;
$(_this.encodeMoreCon).append(img);
$(_this.encodeMoreCon).append($(_this.encodeMoreCon + ' .bg-light:first').clone())
} else if (index >= maxNum) {
return false;
}
});
if (this.encodeLeftImgList.length <= maxNum) {
btn.html('预览已结束,查看全部内容需要购买此文档');
btn.prop('disabled', true);
this.encodeHasLeftView = false;
if (noMroeCallback) {
noMroeCallback()
}
} else {
btn.html('还剩 ' + (this.encodeLeftImgList.length - maxNum) + ' 页未读,点击继续阅读');
if (moreCallback) {
moreCallback()
}
}
}
};
previewMoreCon.init();
$('.show-more-content').click(function () {
$('.describe .content').removeClass('more-content');
$(this).hide();
});
if ($('#contentContainer').outerHeight(true) > 145) {
$('.show-more-content').show();
}