中考几何压轴题

中考几何压轴题

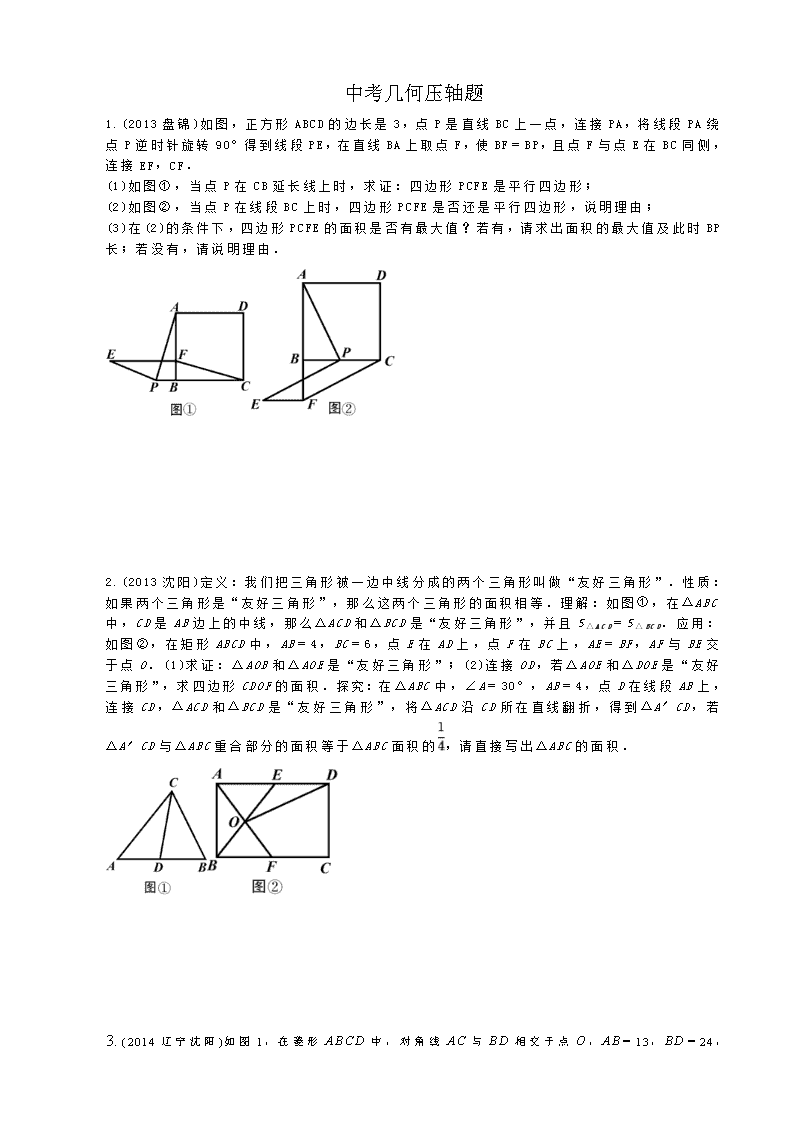
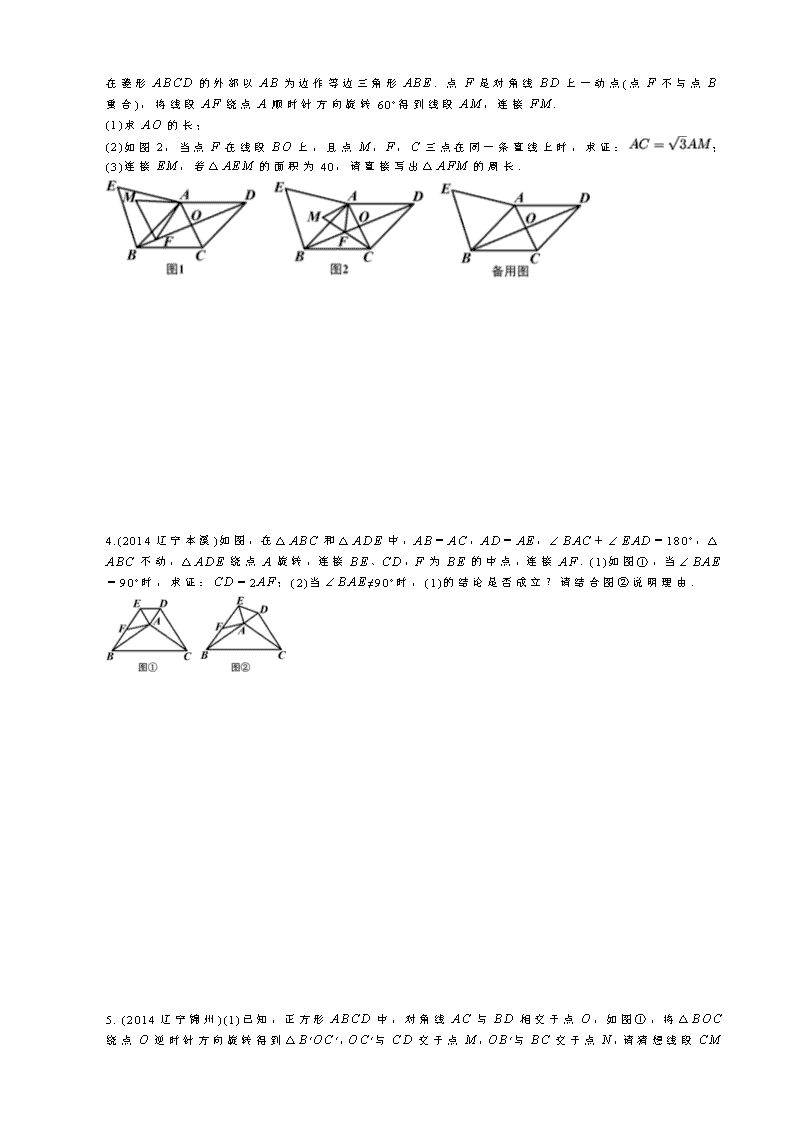
中考几何压轴题 ‎1.(2013盘锦)如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF＝BP，且点F与点E在BC同侧，连接EF，CF． (1)如图①，当点P在CB延长线上时，求证：四边形PCFE是平行四边形； (2)如图②，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由； (3)在(2)的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由． ‎ ‎2.(2013沈阳)定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD＝S△BCD．应用：如图②，在矩形ABCD中，AB＝4，BC＝6，点E在AD上，点F在BC上，AE＝BF，AF与BE交于点O．(1)求证：△AOB和△AOE是“友好三角形”；(2)连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．探究：在△ABC中，∠A＝30°，AB＝4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积． ‎ ‎3. (2014辽宁沈阳)如图1，在菱形ABCD中，对角线AC与BD相交于点O，AB＝13，BD ‎＝24，在菱形ABCD的外部以AB为边作等边三角形ABE．点F是对角线BD上一动点(点F不与点B重合)，将线段AF绕点A顺时针方向旋转60°得到线段AM，连接FM． (1)求AO的长； (2)如图2，当点F在线段BO上，且点M，F，C三点在同一条直线上时，求证：； (3)连接EM，若△AEM的面积为40，请直接写出△AFM的周长． ‎ ‎4.(2014辽宁本溪)如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＋∠EAD＝180°，△ABC不动，△ADE绕点A旋转，连接BE、CD，F为BE的中点，连接AF．(1)如图①，当∠BAE＝90°时，求证：CD＝2AF；(2)当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．‎ ‎5. (2014辽宁锦州)(1)已知，正方形ABCD中，对角线AC与BD相交于点O，如图①，将△BOC绕点O逆时针方向旋转得到△B′OC′，OC′与CD交于点M，OB′与BC交于点N，请猜想线段CM 与BN的数量关系，并证明你的猜想． (2)如图②，将(1)中的△BOC绕点B逆时针旋转得到△BO′C′，连接AO′、DC′，请猜想线段AO′与DC′的数量关系，并证明你的猜想． (3)如图③，已知矩形ABCD和直角△AEF有公共项点A，且∠AEF＝90°，∠EAF＝∠DAC＝α，连接DE、CF，请求出的值(用α的三角函数表示)． ‎ ‎6.(2014辽宁营口)四边形ABCD是正方形，AC与BD相交于点O，点E、F是直线AD上两动点，且AE＝DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H． (1)如图①，当点E、F在线段AD上时，①求证：∠DAG＝∠DCG；②猜想AG与BE的位置关系，并加以证明； (2)如图②，在(1)条件下，连接HO，试说明HO平分∠BHG； (3)当点E、F运动到如图③所示的位置时，其它条件不变，请将图形补充完整，并直接写出∠BHO的度数．‎ ‎ ‎ ‎7. (2014辽宁大连)如图1，△ABC中，AB＝AC，点D在BA的延长线上，点E在BC上，DE＝DC，点F是DE与AC的交点，且DF＝FE． (1)图1中是否存在与∠BDE 相等的角？若存在，请找出，并加以证明，若不存在，说明理由； (2)求证：BE＝EC； (3)若将“点D在BA的延长线上，点E在BC上”和“点F是DE与AC的交点，且DF＝FE”分别改为“点D在AB上，点E在CB的延长线上”和“点F是ED的延长线与AC的交点，且DF＝kFE”，其他条件不变(如图2)．当AB＝1，∠ABC＝a时，求BE的长(用含k、a的式子表示)．‎ ‎8. (2014辽宁丹东)在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ(0°＜θ＜90°)，连接AC1、BD1，AC1与BD1交于点P． (1)如图1，若四边形ABCD是正方形．①求证：△AOC1≌△BOD1．②请直接写出AC1与BD1的位置关系． (2)如图2，若四边形ABCD是菱形，AC＝5，BD＝7，设AC1＝kBD1．判断AC1与BD1的位置关系，说明理由，并求出k的值． (3)如图3，若四边形ABCD是平行四边形，AC＝5，BD＝10，连接DD1，设AC1＝kBD1．请直接写出k的值和AC12＋(kDD1)2的值． ‎ ‎9. (2014辽宁抚顺)已知：Rt△A′BC′≌Rt△ABC，∠A′C′B＝∠ACB＝90°，∠A′BC′＝∠ABC＝60°，Rt△A′BC′可绕点B旋转，设旋转过程中直线CC′和AA′相交于点D． (1)如图1所示，当点C′在AB边上时，判断线段AD和线段A′D之间的数量关系，并证明你的结论；(2)将Rt△A′BC ‎′由图1的位置旋转到图2的位置时，(1)中的结论是否成立？若成立，请证明；若不成立，请说明理由； (3)将Rt△A′BC′由图1的位置按顺时针方向旋转α角(0°≤α≤120°)，当A、C′、A′三点在一条直线上时，请直接写出旋转角的度数．‎ ‎10. (2014辽宁盘锦)已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上(P、G不与正方形顶点重合，且在CD的同侧)，PD＝PG，DF⊥PG于点H，交直线AB于点F，将线段PG绕点P逆时针旋转90°得到线段PE，连结EF． (1)如图1，当点P与点G分别在线段BC与线段AD上时． ①求证：DG＝2PC； ②求证：四边形PEFD是菱形； (2)如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD是怎样的特殊四边形，并证明你的猜想．‎ ‎11. (2014辽宁阜新)已知，在矩形ABCD中，连接对角线AC，将△ABC绕点B顺时针旋转90°得到△EFG，并将它沿直线AB向左平移，直线EG与BC交于点H，连接AH，CG． (1)如图①，当AB＝BC，点F平移到线段BA上时，线段AH，CG有怎样的数量关系和位置关系？直接写出你的猜想； (2)如图②，当AB＝BC，点F平移到线段BA 的延长线上时，(1)中的结论是否成立，请说明理由； (3)如图③，当AB＝nBC(n≠1)时，对矩形ABCD进行如已知同样的变换操作，线段AH，CG有怎样的数量关系和位置关系？直接写出你的猜想．‎ ‎12. (辽宁沈阳)如图，在□ABCD中，AB＝6，BC＝4，∠B＝60°，点E是边AB上一点，点F是边CD上一点，将□ABCD沿EF折叠，得到四边形EFGH，点A的对应点为点H，点D的对应点为点G． (1)当点H与点C重合时． ①填空：点E到CD的距离是________； ②求证：△BCE≌△GCF； ③求△CEF的面积； (2)当点H落在射线BC上，且CH＝1时，直线EH与直线CD交于点M，请直接写出△MEF的面积．‎ ‎13. (2015大连)如图，在△ABC中，点D、E、F分别在AB、BC、AC上，且∠ADF+∠DEC=180°，∠AFE=∠BDE.‎ 如图1，当DE=DF时，图1中是否存在与AB相等的线段？若存在，请找出并加以证明。若不存在说明理由。(2)如图2，当DE=kDF(其中0

查看更多