- 2021-05-10 发布 |
- 37.5 KB |
- 30页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年贵州省贵阳市中考数学试卷
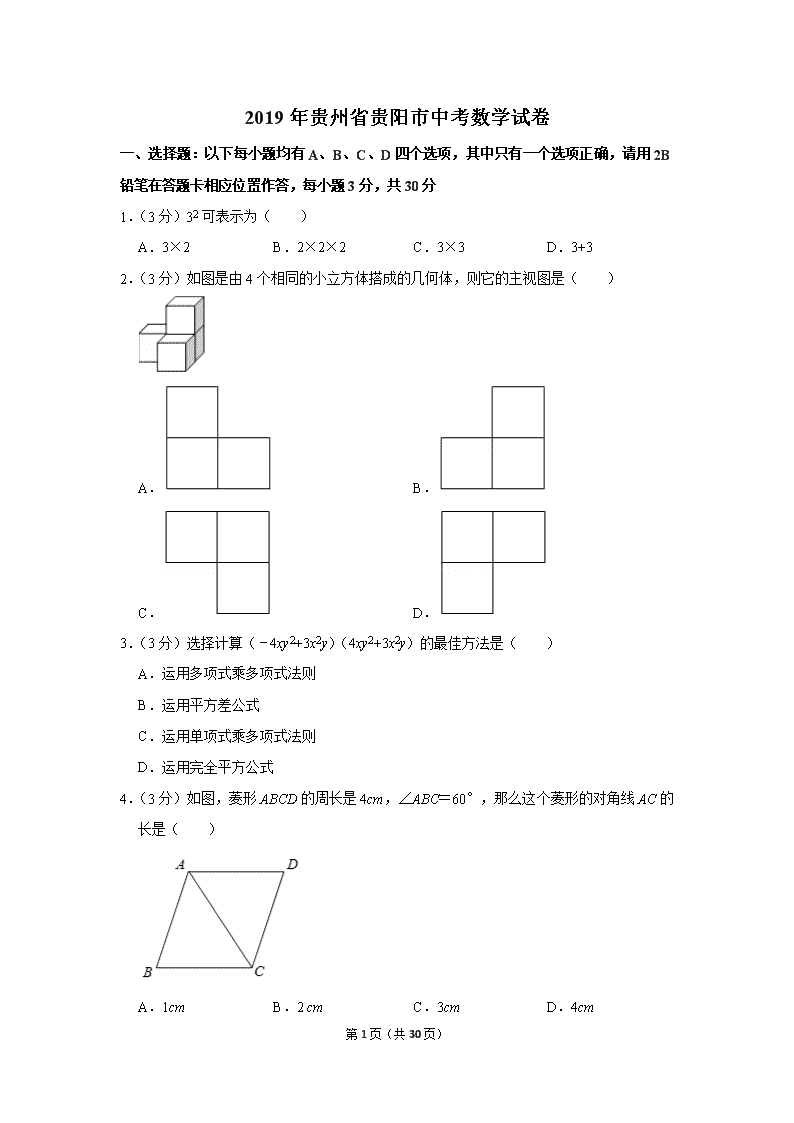
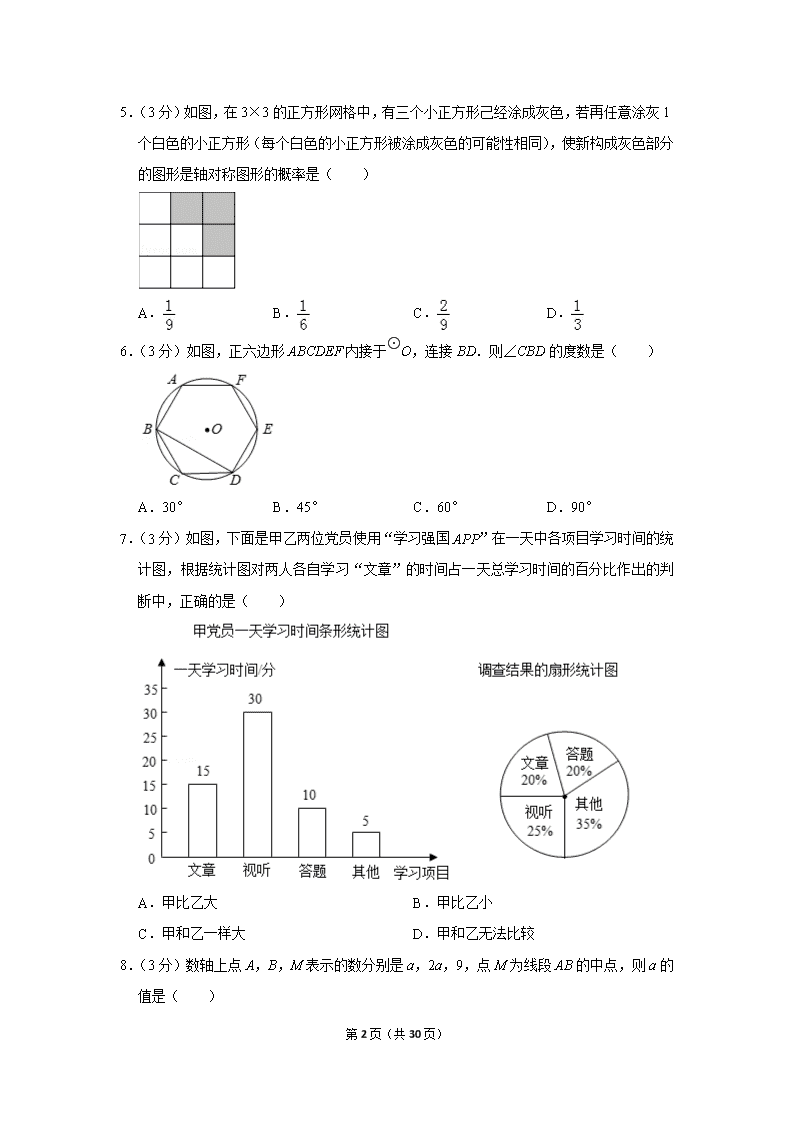
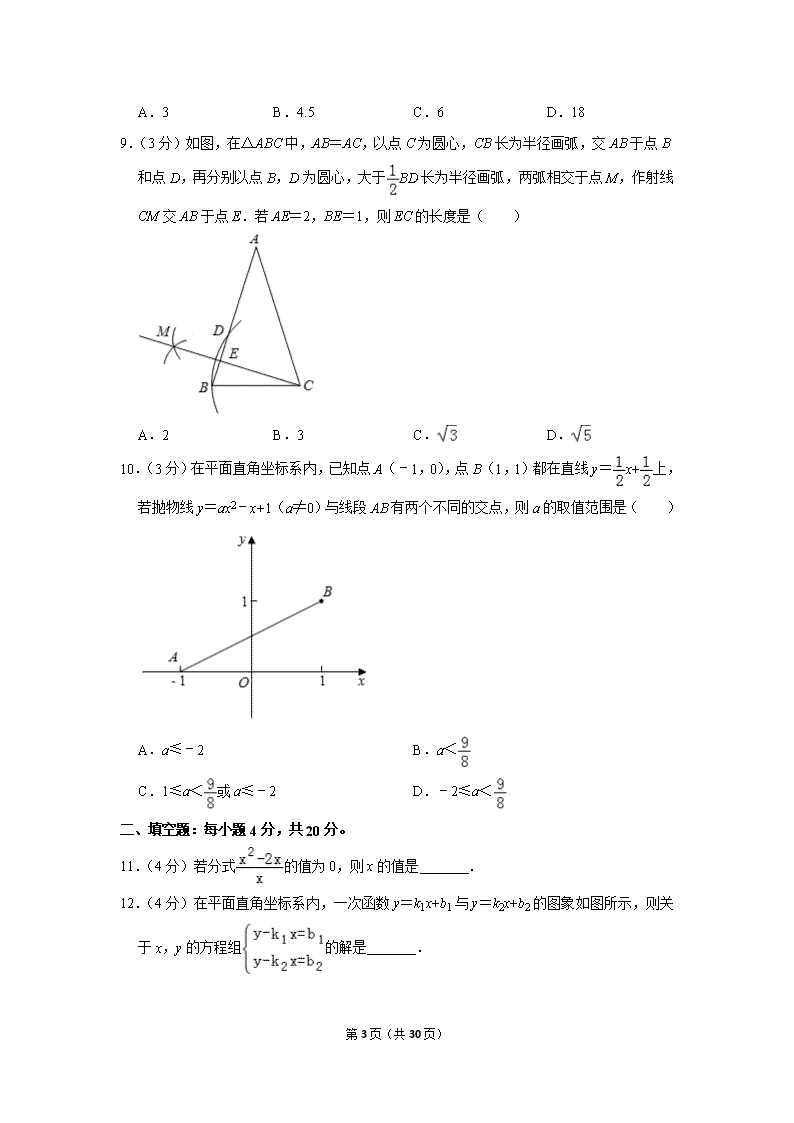
2019年贵州省贵阳市中考数学试卷 一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共30分 1.(3分)32可表示为( ) A.3×2 B.2×2×2 C.3×3 D.3+3 2.(3分)如图是由4个相同的小立方体搭成的几何体,则它的主视图是( ) A. B. C. D. 3.(3分)选择计算(﹣4xy2+3x2y)(4xy2+3x2y)的最佳方法是( ) A.运用多项式乘多项式法则 B.运用平方差公式 C.运用单项式乘多项式法则 D.运用完全平方公式 4.(3分)如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是( ) A.1cm B.2 cm C.3cm D.4cm 第30页(共30页) 5.(3分)如图,在3×3的正方形网格中,有三个小正方形己经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( ) A. B. C. D. 6.(3分)如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( ) A.30° B.45° C.60° D.90° 7.(3分)如图,下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图,根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中,正确的是( ) A.甲比乙大 B.甲比乙小 C.甲和乙一样大 D.甲和乙无法比较 8.(3分)数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( ) 第30页(共30页) A.3 B.4.5 C.6 D.18 9.(3分)如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( ) A.2 B.3 C. D. 10.(3分)在平面直角坐标系内,已知点A(﹣1,0),点B(1,1)都在直线y=x+上,若抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( ) A.a≤﹣2 B.a< C.1≤a<或a≤﹣2 D.﹣2≤a< 二、填空题:每小题4分,共20分。 11.(4分)若分式的值为0,则x的值是 . 12.(4分)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 . 第30页(共30页) 13.(4分)一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出一个球,摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是 . 14.(4分)如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若OA=2,则四叶幸运草的周长是 . 15.(4分)如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是 . 三、解答题:本大题10小题,共100分. 16.(8分)如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形. (1)用含字母a,b的代数式表示矩形中空白部分的面积; (2)当a=3,b=2时,求矩形中空白部分的面积. 第30页(共30页) 17.(10分)为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下: 收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88 (1)根据上述数据,将下列表格补充完整. 整理、描述数据: 成绩/分 88 89 90 91 95 96 97 98 99 学生人数 2 1 3 2 1 2 1 数据分析:样本数据的平均数、众数和中位数如下表 平均数 众数 中位数 93 91 得出结论: (2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为 分. 数据应用: (3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由. 18.(10分)如图,四边形ABCD是平行四边形,延长AD至点E,使DE=AD,连接BD. (1)求证:四边形BCED是平行四边形; (2)若DA=DB=2,cosA=,求点B到点E的距离. 第30页(共30页) 19.(10分)为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等 (1)若从中只录用一人,恰好选到思政专业毕业生的概率是 : (2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率. 20.(10分)某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元. (1)求A,B两款毕业纪念册的销售单价; (2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册. 21.(8分)如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB. (1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围; (2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位) (=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41) 22.(10分)如图,已知一次函数y=﹣2x+8的图象与坐标轴交于A,B两点,并与反比例函数y=的图象相切于点C. (1)切点C的坐标是 ; (2)若点M为线段BC的中点,将一次函数y=﹣2x+8的图象向左平移m(m 第30页(共30页) >0)个单位后,点C和点M平移后的对应点同时落在另一个反比例函数y=的图象上时,求k的值. 23.(10分)如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上. (1)求证:OP∥BC; (2)过点C作⊙O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求⊙O的直径. 24.(12分)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(﹣1,0). (1)求二次函数的表达式; (2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度; (3)当a≤x≤a+1时,二次函数y=x2+bx+c的最小值为2a,求a的值. 25.(12分)(1)数学理解:如图①,△ABC是等腰直角三角形,过斜边AB的中点D 第30页(共30页) 作正方形DECF,分别交BC,AC于点E,F,求AB,BE,AF之间的数量关系; (2)问题解决:如图②,在任意直角△ABC内,找一点D,过点D作正方形DECF,分别交BC,AC于点E,F,若AB=BE+AF,求∠ADB的度数; (3)联系拓广:如图③,在(2)的条件下,分别延长ED,FD,交AB于点M,N,求MN,AM,BN的数量关系. 第30页(共30页) 2019年贵州省贵阳市中考数学试卷 参考答案与试题解析 一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共30分 1.(3分)32可表示为( ) A.3×2 B.2×2×2 C.3×3 D.3+3 【分析】直接利用有理数乘方的意义分析得出答案. 【解答】解:32可表示为:3×3. 故选:C. 【点评】此题主要考查了有理数的乘方,正确把握有理数的乘方定义是解题关键. 2.(3分)如图是由4个相同的小立方体搭成的几何体,则它的主视图是( ) A. B. C. D. 【分析】主视图有2列,每列小正方形数目分别为1,2. 【解答】解:如图所示:它的主视图是:. 故选:B. 【点评】此题主要考查了简单几何体的三视图,正确把握观察角度是解题关键. 3.(3分)选择计算(﹣4xy2+3x2y)(4xy2+3x2y)的最佳方法是( ) 第30页(共30页) A.运用多项式乘多项式法则 B.运用平方差公式 C.运用单项式乘多项式法则 D.运用完全平方公式 【分析】直接利用平方差公式计算得出答案. 【解答】解:选择计算(﹣4xy2+3x2y)(4xy2+3x2y)的最佳方法是:运用平方差公式. 故选:B. 【点评】此题主要考查了多项式乘法,正确应用公式是解题关键. 4.(3分)如图,菱形ABCD的周长是4cm,∠ABC=60°,那么这个菱形的对角线AC的长是( ) A.1cm B.2 cm C.3cm D.4cm 【分析】由于四边形ABCD是菱形,AC是对角线,根据∠ABC=60°,而AB=BC,易证△BAC是等边三角形,从而可求AC的长. 【解答】解:∵四边形ABCD是菱形,AC是对角线, ∴AB=BC=CD=AD, ∵∠ABC=60°, ∴△ABC是等边三角形, ∴AB=BC=AC, ∵菱形ABCD的周长是4cm, ∴AB=BC=AC=1cm. 故选:A. 【点评】本题考查了菱形的性质、等边三角形的判定和性质.菱形的对角线平分对角,解题的关键是证明△ABC是等边三角形. 5.(3分)如图,在3× 第30页(共30页) 3的正方形网格中,有三个小正方形己经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( ) A. B. C. D. 【分析】直接利用轴对称图形的性质分析得出答案. 【解答】解:如图所示:当1,2两个分别涂成灰色,新构成灰色部分的图形是轴对称图形, 故新构成灰色部分的图形是轴对称图形的概率是:=. 故选:D. 【点评】此题主要考查了利用轴对称设计图案,正确掌握轴对称图形的性质是解题关键. 6.(3分)如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( ) A.30° B.45° C.60° D.90° 【分析】根据正六边形的内角和求得∠BCD,然后根据等腰三角形的性质即可得到结论. 【解答】解:∵在正六边形ABCDEF中,∠BCD==120°,BC=CD, ∴∠CBD=(180°﹣120°)=30°, 故选:A. 【点评】本题考查的是正多边形和圆、等腰三角形的性质,三角形的内角和,熟记多边形的内角和是解题的关键. 第30页(共30页) 7.(3分)如图,下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图,根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中,正确的是( ) A.甲比乙大 B.甲比乙小 C.甲和乙一样大 D.甲和乙无法比较 【分析】由扇形统计图可知,乙党员学习文章时间的百分比是20%,再由条形统计图求出甲党员学习文章的百分比,进行比较即可. 【解答】解:由扇形统计图可知,乙党员学习文章时间的百分比是20%, 由条形统计图求出甲党员学习文章的百分比是15÷(15+30+10+5)=25%, 所以甲党员的百分比比乙党员的百分比大. 故选:A. 【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小. 8.(3分)数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点,则a的值是( ) A.3 B.4.5 C.6 D.18 【分析】根据题意列方程即可得到结论. 【解答】解:∵数轴上点A,B,M表示的数分别是a,2a,9,点M为线段AB的中点, ∴9﹣a=2a﹣9, 解得:a=6, 第30页(共30页) 故选:C. 【点评】本题考查了两点间的距离:两点间的连线段长叫这两点间的距离.也考查了数轴. 9.(3分)如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是( ) A.2 B.3 C. D. 【分析】利用基本作图得到CE⊥AB,再根据等腰三角形的性质得到AC=3,然后利用勾股定理计算CE的长. 【解答】解:由作法得CE⊥AB,则∠AEC=90°, AC=AB=BE+AE=2+1=3, 在Rt△ACE中,CE==. 故选:D. 【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线). 10.(3分)在平面直角坐标系内,已知点A(﹣1,0),点B(1,1)都在直线y=x+上,若抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点,则a的取值范围是( ) 第30页(共30页) A.a≤﹣2 B.a< C.1≤a<或a≤﹣2 D.﹣2≤a< 【分析】分a>0,a<0两种情况讨论,根据题意列出不等式组,可求a的取值范围. 【解答】解:∵抛物线y=ax2﹣x+1(a≠0)与线段AB有两个不同的交点, ∴令x+=ax2﹣x+1,则2ax2﹣3x+1=0 ∴△=9﹣8a>0 ∴a< ①当a<0时, 解得:a≤﹣2 ∴a≤﹣2 ②当a>0时, 解得:a≥1 ∴1≤a< 综上所述:1≤a<或a≤﹣2 故选:C. 【点评】本题考查二次函数图象与系数的关系,一次函数图象上点的坐标特征,二次函数图象点的坐标特征,利用分类讨论思想解决问题是本题的关键. 二、填空题:每小题4分,共20分。 11.(4分)若分式的值为0,则x的值是 2 . 【分析】直接利用分式为零的条件分析得出答案. 第30页(共30页) 【解答】解:∵分式的值为0, ∴x2﹣2x=0,且x≠0, 解得:x=2. 故答案为:2. 【点评】此题主要考查了分式的值为零的条件,正确把握定义是解题关键. 12.(4分)在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是 . 【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标求解. 【解答】解:∵一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标为(2,1), ∴关于x,y的方程组的解是. 故答案为. 【点评】本题考查了一次函数与二元一次方程(组):方程组的解就是两个相应的一次函数图象的交点坐标. 13.(4分)一个袋中装有m个红球,10个黄球,n个白球,每个球除颜色外都相同,任意摸出一个球,摸到黄球的概率与不是黄球的概率相同,那么m与n的关系是 m+n=10 . 【分析】直接利用概率相同的频数相同进而得出答案. 【解答】解:∵一个袋中装有m个红球,10个黄球,n个白球,摸到黄球的概率与不是黄球的概率相同, ∴m与n的关系是:m+n=10. 故答案为:m+n=10. 第30页(共30页) 【点评】此题主要考查了概率公式,正确理解概率求法是解题关键. 14.(4分)如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若OA=2,则四叶幸运草的周长是 8π . 【分析】由题意得出:四叶幸运草的周长为4个半圆的弧长=2个圆的周长,由圆的周长公式即可得出结果. 【解答】解:由题意得:四叶幸运草的周长为4个半圆的弧长=2个圆的周长, ∴四叶幸运草的周长=2×2π×2=8π; 故答案为:8π. 【点评】本题考查了正多边形和圆、正方形的性质以及圆周长公式;由题意得出四叶幸运草的周长=2个圆的周长是解题的关键. 15.(4分)如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是 . 【分析】当F与A点重合时和F与C重合时,根据E的位置,可知E的运动路径是EE'的长;由已知条件可以推导出△DEE'是直角三角形,且∠DEE'=30°,在Rt△ADE'中,求出DE'=即可求解. 【解答】解:E的运动路径是EE'的长; ∵AB=4,∠DCA=30°, ∴BC=, 当F与A点重合时, 在Rt△ADE'中,AD=,∠DAE'=30°,∠ADE'=60°, 第30页(共30页) ∴DE'=,∠CDE'=30°, 当F与C重合时,∠EDC=60°, ∴∠EDE'=90°,∠DEE'=30°, 在Rt△DEE'中,EE'=; 故答案为. 【点评】本题考查点的轨迹;能够根据E点的运动情况,分析出E点的运动轨迹是线段,在30度角的直角三角形中求解是关键. 三、解答题:本大题10小题,共100分. 16.(8分)如图是一个长为a,宽为b的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形. (1)用含字母a,b的代数式表示矩形中空白部分的面积; (2)当a=3,b=2时,求矩形中空白部分的面积. 【分析】(1)空白区域面积=矩形面积﹣两个阴影平行四边形面积+中间重叠平行四边形面积; (2)将a=3,b=2代入(1)中即可; 【解答】解:(1)S=ab﹣a﹣b+1; 第30页(共30页) (2)当a=3,b=2时,S=6﹣3﹣2+1=2; 【点评】本题考查阴影部分面积,平行四边形面积,代数式求值;能够准确求出阴影部分面积是解题的关键. 17.(10分)为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩,数据如下: 收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88 (1)根据上述数据,将下列表格补充完整. 整理、描述数据: 成绩/分 88 89 90 91 95 96 97 98 99 学生人数 2 1 5 3 2 1 3 2 1 数据分析:样本数据的平均数、众数和中位数如下表 平均数 众数 中位数 93 90 91 得出结论: (2)根据所给数据,如果该校想确定七年级前50%的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为 91 分. 数据应用: (3)根据数据分析,该校决定在七年级授予测评成绩前30%的学生“禁毒小卫士”荣誉称号,请估计评选该荣誉称号的最低分数,并说明理由. 【分析】(1)由题意即可得出结果; (2)由20×50%=10,结合题意即可得出结论; (3)由20×30%=6,即可得出结论. 【解答】解:(1)由题意得:90分的有5个;97分的有3个; 出现次数最多的是90分, ∴众数是90分; 故答案为:5;3;90; 第30页(共30页) (2)20×50%=10, 如果该校想确定七年级前50%的学生为“良好”等次,则“良好”等次的测评成绩至少定为91分; 故答案为:91; (3)估计评选该荣誉称号的最低分数为97分;理由如下: ∵20×30%=6, ∴估计评选该荣誉称号的最低分数为97分. 【点评】本题考查了众数、中位数、用样本估计总体等知识;熟练掌握众数、中位数、用样本估计总体是解题的关键. 18.(10分)如图,四边形ABCD是平行四边形,延长AD至点E,使DE=AD,连接BD. (1)求证:四边形BCED是平行四边形; (2)若DA=DB=2,cosA=,求点B到点E的距离. 【分析】(1)根据平行四边形的性质得到AD=BC,AD∥BC,等量代换得到DE=BC,DE∥BC,于是得到四边形BCED是平行四边形; (2)连接BE,根据已知条件得到AD=BD=DE=2,根据直角三角形的判定定理得到∠ABE=90°,AE=4,解直角三角形即可得到结论. 【解答】(1)证明:∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC, ∵DE=AD, ∴DE=BC,DE∥BC, ∴四边形BCED是平行四边形; (2)解:连接BE, ∵DA=DB=2,DE=AD, ∴AD=BD=DE=2, ∴∠ABE=90°,AE=4, 第30页(共30页) ∵cosA=, ∴AB=1, ∴BE==. 【点评】本题考查了平行四边形的判定和性质,直角三角形的判定和性质,三角函数的定义,证得∠ABE=90°是解题的关键. 19.(10分)为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等 (1)若从中只录用一人,恰好选到思政专业毕业生的概率是 : (2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率. 【分析】(1)由概率公式即可得出结果; (2)设思政专业的一名研究生为A、一名本科生为B,历史专业的一名研究生为C、一名本科生为D,画树状图可知:共有12个等可能的结果,恰好选到的是一名思政研究生和一名历史本科生的结果有2个,即可得出结果. 【解答】解:(1)若从中只录用一人,恰好选到思政专业毕业生的概率是=; 故答案为:; (2)设思政专业的一名研究生为A、一名本科生为B,历史专业的一名研究生为C、一名本科生为D, 画树状图如图: 共有12个等可能的结果,恰好选到的是一名思政研究生和一名历史本科生的结果有2个, ∴恰好选到的是一名思政研究生和一名历史本科生的概率为=. 第30页(共30页) 【点评】本题考查了列表法与树状图法以及概率公式;根据题意画出树状图是解题的关键. 20.(10分)某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元. (1)求A,B两款毕业纪念册的销售单价; (2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册. 【分析】(1)直接利用第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元,分别得出方程求出答案; (2)利用不超过529元购买这两种款式的毕业纪念册共60本,得出不等式求出答案. 【解答】解:(1)设A款毕业纪念册的销售为x元,B款毕业纪念册的销售为y元,根据题意可得: , 解得:, 答:A款毕业纪念册的销售为10元,B款毕业纪念册的销售为8元; (2)设能够买a本A款毕业纪念册,则购买B款毕业纪念册(60﹣a)本,根据题意可得: 10a+8(60﹣a)≤529, 解得:a≤24.5, 则最多能够买24本A款毕业纪念册. 【点评】此题主要考查了一元一次不等式的应用以及二元一次方程组的应用,正确得出等量关系是解题关键. 21.(8分)如图所示是我国古代城市用以滞洪或分洪系统的局部截面原理图,图中OP为下水管道口直径,OB为可绕转轴O自由转动的阀门.平时阀门被管道中排出的水冲开,可排出城市污水;当河水上涨时,阀门会因河水压迫而关闭,以防河水倒灌入城中.若阀门的直径OB=OP=100cm,OA为检修时阀门开启的位置,且OA=OB. 第30页(共30页) (1)直接写出阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围; (2)为了观测水位,当下水道的水冲开阀门到达OB位置时,在点A处测得俯角∠CAB=67.5°,若此时点B恰好与下水道的水平面齐平,求此时下水道内水的深度.(结果保留小数点后一位) (=1.41,sin67.5°=0.92,cos67.5°=0.38,tan67.5°=2.41,sin22.5°=0.38,cos22.5°=0.92,tan22.5°=0.41) 【分析】(1)根据题意即可得到结论; (2)根据余角的定义得到∠BAO=22.5°,根据等腰三角形的性质得到∠BAO=∠ABO=22.5°,由三角形的外角的性质得到∠BOP=45°,解直角三角形即可得到结论. 【解答】解:(1)阀门被下水道的水冲开与被河水关闭过程中∠POB的取值范围为:90°≤∠POB≤0°; (2)如图,∵∠CAB=67.5°, ∴∠BAO=22.5°, ∵OA=OB, ∴∠BAO=∠ABO=22.5°, ∴∠BOP=45°, ∵OB=100, ∴OE=OB=50, ∴PE=OP﹣OE=100﹣50≈29.5cm, 答:此时下水道内水的深度约为29.5cm. 第30页(共30页) 【点评】此题考查了考查俯角的定义,要求学生能借助俯角构造直角三角形并解直角三角形.注意方程思想与数形结合思想的应用. 22.(10分)如图,已知一次函数y=﹣2x+8的图象与坐标轴交于A,B两点,并与反比例函数y=的图象相切于点C. (1)切点C的坐标是 (2,4) ; (2)若点M为线段BC的中点,将一次函数y=﹣2x+8的图象向左平移m(m>0)个单位后,点C和点M平移后的对应点同时落在另一个反比例函数y=的图象上时,求k的值. 【分析】(1)将一次函数解析式与反比例函数解析式组成方程组,求解即可; (2)先求出点M坐标,再求出点C和点M平移后的对应点的坐标,列出方程可求m和k的值. 【解答】解:(1)∵一次函数y=﹣2x+8的图象与反比例函数y=的图象相切于点C ∴﹣2x+8= ∴x=2, ∴点C坐标为(2,4) 故答案为:(2,4); (2)∵一次函数y=﹣2x+8的图象与坐标轴交于A,B两点, 第30页(共30页) ∴点B(4,0) ∵点M为线段BC的中点, ∴点M(3,2) ∴点C和点M平移后的对应点坐标分别为(2﹣m,4),(3﹣m,2) ∴k=4(2﹣m)=2(3﹣m) ∴m=1 ∴k=4 【点评】本题是反比例函数与一次函数的综合题,一次函数的性质和反比例函数的性质,由点的坐标在函数图象上列等式可解决问题. 23.(10分)如图,已知AB是⊙O的直径,点P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上. (1)求证:OP∥BC; (2)过点C作⊙O的切线CD,交AP的延长线于点D.如果∠D=90°,DP=1,求⊙O的直径. 【分析】(1)由题意可知=,根据同弧所对的圆心角相等得到∠AOP=∠POC=∠AOC,再根据同弧所对的圆心角和圆周角的关系得出∠ABC=∠AOC,利用同位角相等两直线平行,可得出PO与BC平行; (2)由CD为圆O的切线,利用切线的性质得到OC垂直于CD,又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行,根据两直线平行内错角相等得到∠APO=∠COP,由∠AOP=∠COP,等量代换可得出∠APO=∠AOP,再由OA=OP,利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形,根据等边三角形的内角为60°得到∠AOP为60°,由OP平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°,再由OB=OC,得到三角形OBC为等边三角形,可得出∠COB为60°,利用平角的定义得到∠POC 第30页(共30页) 也为60°,再加上OP=OC,可得出三角形POC为等边三角形,得到内角∠OCP为60°,可求出∠PCD为30°,在直角三角形PCD中,利用30°所对的直角边等于斜边的一半可得出PD为PC的一半,而PC等于圆的半径OP等于直径AB的一半,可得出PD为AB的四分之一,即AB=4PD=4. 【解答】(1)证明:∵A关于OP的对称点C恰好落在⊙O上. ∴= ∴∠AOP=∠COP, ∴∠AOP=∠AOC, 又∵∠ABC=∠AOC, ∴∠AOP=∠ABC, ∴PO∥BC; (2)解:连接PC, ∵CD为圆O的切线, ∴OC⊥CD,又AD⊥CD, ∴OC∥AD, ∴∠APO=∠COP, ∵∠AOP=∠COP, ∴∠APO=∠AOP, ∴OA=AP, ∵OA=OP, ∴△APO为等边三角形, ∴∠AOP=60°, 又∵OP∥BC, ∴∠OBC=∠AOP=60°,又OC=OB, ∴△BCO为等边三角形, ∴∠COB=60°, ∴∠POC=180°﹣(∠AOP+∠COB)=60°,又OP=OC, ∴△POC也为等边三角形, 第30页(共30页) ∴∠PCO=60°,PC=OP=OC, 又∵∠OCD=90°, ∴∠PCD=30°, 在Rt△PCD中,PD=PC, 又∵PC=OP=AB, ∴PD=AB, ∴AB=4PD=4. 【点评】此题考查了切线的性质,等边三角形的判定与性质,含30°直角三角形的性质,轴对称的性质,圆周角定理,以及平行线的判定与性质,熟练掌握性质及判定是解本题的关键. 24.(12分)如图,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,且关于直线x=1对称,点A的坐标为(﹣1,0). (1)求二次函数的表达式; (2)连接BC,若点P在y轴上时,BP和BC的夹角为15°,求线段CP的长度; (3)当a≤x≤a+1时,二次函数y=x2+bx+c的最小值为2a,求a的值. 【分析】(1)先根据题意得出点B的坐标,再利用待定系数法求解可得; (2)分点P在点C上方和下方两种情况,先求出∠OBP的度数,再利用三角函数求出OP 第30页(共30页) 的长,从而得出答案; (3)分对称轴x=1在a到a+1范围的右侧、中间和左侧三种情况,结合二次函数的性质求解可得. 【解答】解:(1)∵点A(﹣1,0)与点B关于直线x=1对称, ∴点B的坐标为(3,0), 代入y=x2+bx+c,得: , 解得, 所以二次函数的表达式为y=x2﹣2x﹣3; (2)如图所示: 由抛物线解析式知C(0,﹣3), 则OB=OC=3, ∴∠OBC=45°, 若点P在点C上方,则∠OBP=∠OBC﹣∠PBC=30°, ∴OP=OBtan∠OBP=3×=, ∴CP=3﹣; 若点P在点C下方,则∠OBP′=∠OBC+∠P′BC=60°, ∴OP′=OBtan∠OBP′=3×=3, ∴CP=3﹣3; 综上,CP的长为3﹣或3﹣3; 第30页(共30页) (3)若a+1<1,即a<0, 则函数的最小值为(a+1)2﹣2(a+1)﹣3=2a, 解得a=1﹣(正值舍去); 若a<1<a+1,即0<a<1, 则函数的最小值为1﹣2﹣3=2a, 解得:a=﹣2(舍去); 若a>1, 则函数的最小值为a2﹣2a﹣3=2a, 解得a=2+(负值舍去); 综上,a的值为1﹣或2+. 【点评】本题是二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、三角函数的运用、二次函数的图象与性质及分类讨论思想的运用. 25.(12分)(1)数学理解:如图①,△ABC是等腰直角三角形,过斜边AB的中点D作正方形DECF,分别交BC,AC于点E,F,求AB,BE,AF之间的数量关系; (2)问题解决:如图②,在任意直角△ABC内,找一点D,过点D作正方形DECF,分别交BC,AC于点E,F,若AB=BE+AF,求∠ADB的度数; (3)联系拓广:如图③,在(2)的条件下,分别延长ED,FD,交AB于点M,N,求MN,AM,BN的数量关系. 【分析】数学理解: (1)由等腰直角三角形的性质可得AC=BC,∠A=∠B=45°,AB=AC,由正方形的性质可得DE=DF=CE,∠DFC=∠DEC=90°,可求AF=DF=CE,即可得AB=(AF+BE); 问题解决: (2)延长AC,使FM=BE,通过证明△DFM≌△DEB,可得DM=DB,通过△ADM≌△ADB,可得∠DAC=∠DAB=∠CAB,∠ABD=∠CBD=∠ABC 第30页(共30页) ,由三角形内角和定理可求∠ADB的度数; 联系拓广: (3)由正方形的性质可得DE∥AC,DF∥BC,由平行线的性质可得∠DAB=∠ADM,∠NDB=∠ABD,可得AM=MD,DN=NB,即可求MN,AM,BN的数量关系. 【解答】解: 数学理解: (1)AB=(AF+BE) 理由如下:∵△ABC是等腰直角三角形 ∴AC=BC,∠A=∠B=45°,AB=AC6 ∵四边形DECF是正方形 ∴DE=DF=CE=CF,∠DFC=∠DEC=90° ∴∠A=∠ADF=45° ∴AF=DF=CE ∴AF+BE=BC=AC ∴AB=(AF+BE) 问题解决: (2)如图,延长AC,使FM=BE,连接DM, ∵四边形DECF是正方形 ∴DF=DE,∠DFC=∠DEC=90° ∵BE=FM,∠DFC=∠DEB=90°,DF=ED ∴△DFM≌△DEB(SAS) ∴DM=DB 第30页(共30页) ∵AB=AF+BE,AM=AF+FM,FM=BE, ∴AM=AB,且DM=DB,AD=AD ∴△ADM≌△ADB(SSS) ∴∠DAC=∠DAB=∠CAB 同理可得:∠ABD=∠CBD=∠ABC ∵∠ACB=90°, ∴∠CAB+∠CBA=90° ∴∠DAB+∠ABD=(∠CAB+∠CBA)=45° ∴∠ADB=180°﹣(∠DAB+∠ABD)=135° 联系拓广: (3)∵四边形DECF是正方形 ∴DE∥AC,DF∥BC ∴∠CAD=∠ADM,∠CBD=∠NDB,∠MDN=∠AFD=90° ∵∠DAC=∠DAB,∠ABD=∠CBD ∴∠DAB=∠ADM,∠NDB=∠ABD ∴AM=MD,DN=NB 在Rt∠DMN中,MN2=MD2+DN2, ∴MN2=AM2+NB2, 【点评】本题是四边形综合题,考查了正方形的性质,等腰三角形的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造全等三角形是本题的关键. 声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布 日期:2019/7/7 17:38:50;用户:柯瑞;邮箱:ainixiaoke00@163.com;学号:500557 第30页(共30页)查看更多