2017中考复习 三角形综合题

2017中考复习 三角形综合题

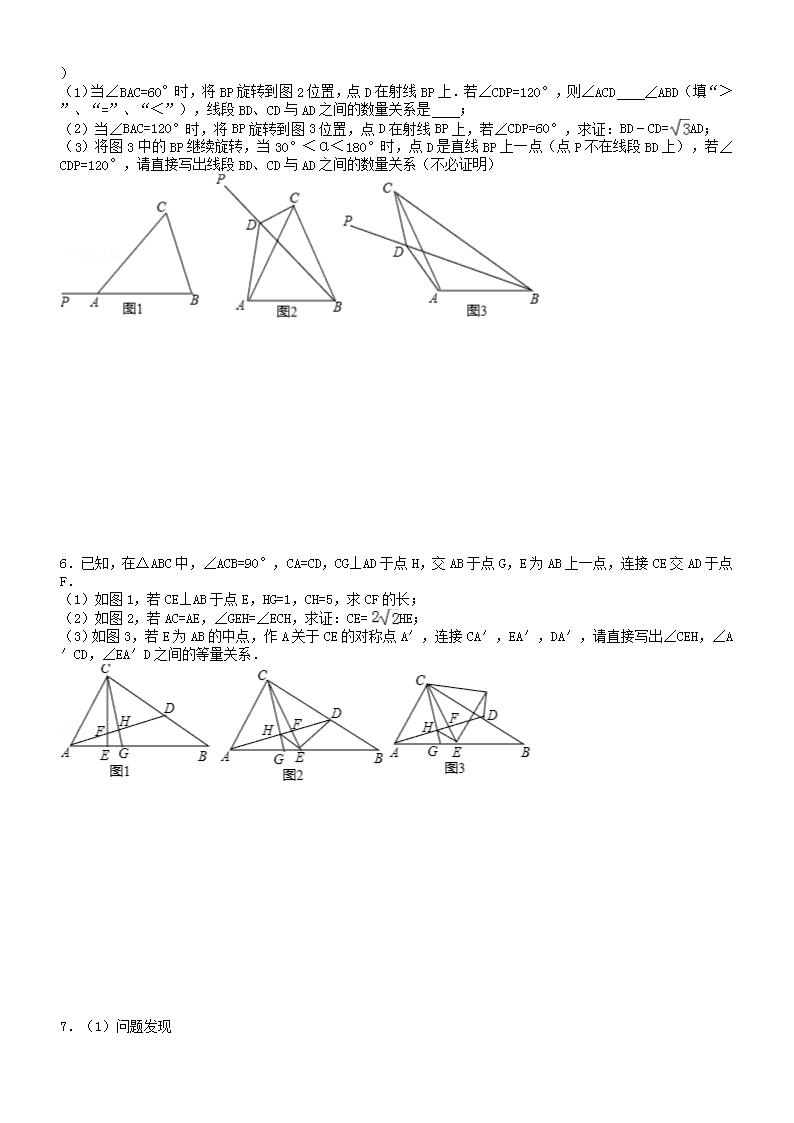
三角形综合题 ‎1．已知，如图，Rt△ABC中，∠ACB=90°，BC=8，cot∠BAC=，点D在边BC上（不与点B、C重合），点E在边BC的延长线上，∠DAE=∠BAC，点F在线段AE上，∠ACF=∠B．设BD=x．‎ ‎（1）若点F恰好是AE的中点，求线段BD的长；‎ ‎（2）若y=，求y关于x的函数关系式，并写出它的定义域；‎ ‎（3）当△ADE是以AD为腰的等腰三角形时，求线段BD的长．‎ ‎2．如图，△ABC边AB上点D、E（不与点A、B重合），满足∠DCE=∠ABC，∠ACB=90°，AC=3，BC=4；‎ ‎（1）当CD⊥AB时，求线段BE的长；‎ ‎（2）当△CDE是等腰三角形时，求线段AD的长；‎ ‎（3）设AD=x，BE=y，求y关于x的函数解析式，并写出定义域．‎ ‎3．如图，已知△ABC中，AB=AC=3，BC=2，点D是边AB上的动点，过点D作DE∥BC，交边AC于点E，点Q是线段DE上的点，且QE=2DQ，连接BQ并延长，交边AC于点P．设BD=x，AP=y．‎ ‎（1）求y关于x的函数解析式及定义域；‎ ‎（2）当△PQE是等腰三角形时，求BD的长；‎ ‎（3）连接CQ，当∠CQB和∠CBD互补时，求x的值．‎ ‎4．如图，在Rt△ABC中，∠ACB=90°，=，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．‎ ‎（1）探究发现：‎ 如图1，若m=n，点E在线段AC上，则=　　；‎ ‎（2）数学思考：‎ ‎①如图2，若点E在线段AC上，则=　　（用含m，n的代数式表示）；‎ ‎②当点E在直线AC上运动时，①中的结论是否任然成立？请仅就图3的情形给出证明；‎ ‎（3）拓展应用：若AC=，BC=2，DF=4，请直接写出CE的长．‎ ‎5．如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°‎ ‎）‎ ‎（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD　　∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是　　；‎ ‎（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=AD；‎ ‎（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）‎ ‎6．已知，在△ABC中，∠ACB=90°，CA=CD，CG⊥AD于点H，交AB于点G，E为AB上一点，连接CE交AD于点F．‎ ‎（1）如图1，若CE⊥AB于点E，HG=1，CH=5，求CF的长；‎ ‎（2）如图2，若AC=AE，∠GEH=∠ECH，求证：CE=HE；‎ ‎（3）如图3，若E为AB的中点，作A关于CE的对称点A′，连接CA′，EA′，DA′，请直接写出∠CEH，∠A′CD，∠EA′D之间的等量关系．‎ ‎7．（1）问题发现 如图1，在Rt△ABC中，∠A=90°，=1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD．‎ 填空：①=　　；②∠ACD的度数为　　．‎ ‎（2）拓展探究 如图2，在Rt△ABC中，∠A=90°，=k．点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B的数量关系以及PB与CD之间的数量关系，并说明理由．‎ ‎（3）解决问题 如图3，在△ABC中，∠B=45°，AB=4，BC=12，P是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD．若PA=5，请直接写出CD的长．‎ ‎8．Rt△ABC与Rt△DEF的位置如图所示，其中AC=2，BC=6，DE=3，∠D=30°，其中，Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动，射线DE、DF与射线AB分别交于N、M两点，运动时间为t，当点E运动到与点B重合时停止运动．‎ ‎（1）当Rt△DEF在起始时，求∠AMF的度数；‎ ‎（2）设BC的中点的为P，当△PBM为等腰三角形时，求t的值；‎ ‎（3）若两个三角形重叠部分的面积为S，写出S与t的函数关系式和相应的自变量的取值范围．‎ ‎9．如图，已知等腰△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD的中点，连接FE、ED，BF的延长线交ED的延长线于点G，连接GC．‎ ‎（1）求证：EF∥CG；‎ ‎（2）若AC=AB，求证：AC=CG；‎ ‎（3）如图2，若CG=EG，则=　　．‎ ‎10．在Rt△ABC中，∠CAB=90°，AC=AB=6，D，E分别是AB，AC的中点，若等腰Rt△ADE绕点A逆时针旋转，得到Rt△AD1E1，设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．‎ ‎（1）如图1，当α=90°时，线段BD1的长等于　　，线段CE1的长等于　　；‎ ‎（2）如图2，当α=135°时，设直线BD1与CA的交点为F，求证：BD1=CE1，且BD1⊥CE1；‎ ‎（3）点P到AB所在直线的距离的最大值是　　．‎ ‎11．如图，在Rt△ABC中，∠ACB=90°，点D为边BC上任意一点，以直线AD为对称轴，作Rt△ABC的轴对称图形Rt△AEF，点M、点N、点P、点Q分别为AB、BC、EF、EA的中点．‎ ‎（1）求证：MN=PQ；‎ ‎（2）如图2，当BD=时，判断点M、点N、点P、点Q围成的四边形的形状，并说明理由；‎ ‎（3）若BC=6，请你直接写出当①BD=3；②BD=6时，点M、点N、点P、点Q围成图形的形状．‎ ‎12．在Rt△ABC中，∠ACB=90°，点D在AB边上，AD=BD，过点D作射线DH，交BC边于点M．‎ ‎（1）如图1，若∠B=30°，求证：△ACD是等边三角形；‎ ‎（2）如图2，若AC=10，AD=13，∠CDH=∠A．‎ ‎①求线段DM的长；‎ ‎②点P是射线DH上一点，连接AP交CD于点N，当△DMN是等腰三角形时，求线段MP的长．‎ ‎13．等腰三角形ABC中，AB=CB，BO⊥AC，点P为射线BC上的动点（不与点B重合），在射线CA上截取CD=CB，作PF⊥BD，分别交射线BO，BD于点E，F．设∠ABC=α．‎ ‎（1）令∠ABC=90°．‎ ‎①如图1，当点P与点C重合时，求证：△BOD≌△POE；‎ ‎②如图2，当点P在点C的左边时，求的值；‎ ‎③猜想：当点P在点C的右边时，的值又是多少？‎ 请直接写出．‎ ‎（2）设点P在点C的右边，请在图3（∠ABC＞90°）或图4（∠ABC＜90°）中继续探究的值（用含α的式子表示），并说明理由．‎ ‎14．如图1，△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E在AC边上，连接BE．‎ ‎（1）若AF是△ABE的中线，且AF=5，AE=6，连接DF，求DF的长；‎ ‎（2）若AF是△ABE的高，延长AF交BC于点G．‎ ‎①如图2，若点E是AC的中点，连接EG，求证：AG+EG=BE；‎ ‎②如图3，若点E是AC边上的动点，连接DF．当点E在AC边上（不含端点）运动时，∠DFG的大小是否改变，如果不变，请求出∠DFG的度数；如果要变，请说明理由．‎ ‎15．在△ABC中，AD、AE分别是△ABC的内、外角平分线．‎ ‎（1）如图①，CG⊥AD于G，BG的延长线交AE于H，求证：AH=EH；‎ ‎（2）如图①，在（1）的条件下，若AE=2AD，BE=5BC，则tan∠AHB=　　；‎ ‎（3）如图②，点M是DE的中点，BE=5BC=10，求MD的长．‎ ‎16．如图，△ABC是等边三角形，AB=2，D是边BC的中点，点P从点A出发，沿AB﹣‎ BD以每秒1个单位长度的速度向终点D运动．同时点Q从点C出发，沿CA﹣AC以每秒1个单位长度的速度运动．当点P停止运动时，点Q也随之停止运动，设点P的运动时间为t（秒），△PQD的面积为S．‎ ‎（1）求线段PB的长（用含t的代数式）．‎ ‎（2）当△PQD是等边三角形时，求t的值．‎ ‎（3）当S＞0时，求S与t的函数关系式．‎ ‎（4）若点D关于直线PQ的对称点为点D′，且S＞0，直接写出点D′落在△ABC的边上时t的值．‎ ‎17．在Rt△AOB中，OA=3，sinB=，P、M、分别是BA、BO边上的两个动点．点M从点B出发，沿BO以1单位/秒的速度向点O运动；点P从点B出发，沿BA以a单位/秒的速度向点A运动；P、M两点同时出发，任意一点先到达终点时，两点停止运动．设运动的时间为t．‎ ‎（1）线段AP的长度为　　（用含a、t的代数式表示）；‎ ‎（2）如图①，连结PO、PM，若a=1，△PMO的面积为S，试求S的最大值；‎ ‎（3）如图②，连结PM、AM，试探究：在点P、M运动的过程中，是否存在某个时刻，使得△PMB为直角三角形且△PMA是等腰三角形？若存在，求出此时a和t的取值，若不存在，请说明理由．‎ ‎18．在直角△ABC中，∠ACB=90°，点E在AC边上，连结BE，作∠ACF=∠‎ CBE交AB于点F，同时点D在BE上，且CD⊥AB．‎ ‎（1）已知：如图，，．‎ ‎①求证：△ACF≌△BCD．‎ ‎②求的值．‎ ‎（2）若，，则的值是多少（直接写出结果）‎ ‎19．已知，AB=5，tan∠ABM=，点C、D、E为动点，其中点C、D在射线BM上（点C在点D的左侧），点E和点D分别在射线BA的两侧，且AC=AD，AB=AE，∠CAD=∠BAE．‎ ‎（1）当点C与点B重合时（如图1），联结ED，求ED的长；‎ ‎（2）当EA∥BM时（如图2），求四边形AEBD的面积；‎ ‎（3）联结CE，当△ACE是等腰三角形时，求点B、C间的距离．‎ ‎20．在△ABC中，D、E、F分别为BC、AB、AC上的点．‎ ‎（1）如图1，若EF∥BC、DF∥AB，连CE、AD分别交DF、EF于N、M，且E为AB的中点，求证：EM=MF；‎ ‎（2）如图2，在（1）中，若E不是AB的中点，请写出与MN平行的直线，并证明；‎ ‎（3）若BD=DC，∠B=90°，且AE：AB：BC=1：3：2，AD与CE相交于点Q，直接写出tan∠CQD的值．‎ ‎21．我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P．像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．‎ 特例探索 ‎（1）①如图1，当∠ABE=45°，时，a=　　，b=　　；‎ ‎②如图2，当∠ABE=30°，c=4时，求a和b的值 归纳证明 ‎（2）请你观察（1）中的计算结果，猜想三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．‎ ‎22．如图，一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动，移动过程中始终有AB⊥ON于点B，AC⊥OM于点A，∠MON的平分线OP分别交AB，AC于点D、E．‎ ‎（1）点A在移动的过程中，线段AD和AE有怎样的数量关系？（不必证明）‎ ‎（2）点A在移动的过程中，若射线ON上始终存在一点F与点A关于OP所在的直线对称，判断并证明以A、D、F、E为顶点的四边形是什么特殊四边形？‎ ‎（3）若∠MON=45°，猜想线段AC、AD、OC之间有怎样的数量关系？请证明你的猜想．‎ ‎23．如图①，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与点A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM，射线AE于点F、D．‎ ‎（1）问题发现：直接写出∠NDE=　　度；‎ ‎（2）拓展探究：试判断，如图②当∠EAC为钝角时，其他条件不变，∠NDE的大小有无变化？请给出证明．‎ ‎（3）如图③，若∠EAC=15°，BD=，直线CM与AB交于点G，其他条件不变，请直接写出AC的长．‎ ‎24．在△ABC中，∠ABC=2∠ACB，延长AB至点D，使BD=BC，点E是直线BC上一点，点F是直线AC上一点，连接DE．连接EF，且∠DEF=∠DBC．‎ ‎（1）如图1，若∠D=∠EFC=15°，AB=，求AC的长．‎ ‎（2）如图2，当∠BAC=45°，点E为线段BC的延长线上，点F在线段AC的延长线上时，求证：CF=BE．‎ ‎（3）如图3，当∠BAC=90°，点E为线段CB的延长线上，点F在线段CA的延长线上时，猜想线段CF与线段BE的数量关系，并证明猜想的结论．‎ ‎25．中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形！‎ ‎（1）如图1，若点D为等腰直角三角形ABC斜边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°，连接AD、EF，当BC=5，FC=2时，求EF的长度；‎ ‎（2）如图2，若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°；M为EF的中点，连接CM，当DF∥AB时，证明：3ED=2MC；‎ ‎（3）如图3，若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°；当BE=6，CF=0.8时，直接写出EF的长度．‎ ‎26．已知，△ABC为直角三角形，∠ACB=90°，点P是射线CB上一点（点P不与点B、C重合），线段AP绕点A顺时针旋转90°得到线段AQ，连接QB交射线AC于点M．‎ ‎（1）如图①，当AC=BC，点P在线段CB上时，线段PB、CM的数量关系是　　；‎ ‎（2）如图②，当AC=BC，点P在线段CB的延长线时，（1）中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由．‎ ‎（3）如图③，若，点P在线段CB的延长线上，CM=2，AP=13，求△ABP的面积．‎ ‎27．在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．‎ ‎（1）如图1，若点F与点A重合，求证：AC=BC；‎ ‎（2）若∠DAF=∠DBA，‎ ‎①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；‎ ‎②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．‎ ‎28．如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．‎ ‎（1）求证：DE⊥AG；‎ ‎（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．‎ ‎①在旋转过程中，当∠OAG′是直角时，求α的度数；‎ ‎②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．‎ ‎29．在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E．DF与线段AC（或AC的延长线）相交于点F．‎ ‎（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；‎ ‎（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=AB；‎ ‎（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线相交于点F，作DN⊥AC于点N，若DN⊥AC于点N，若DN=FN，求证：BE+CF=（BE﹣CF）．‎ ‎30．如图1所示，在菱形ABCD和菱形AEFG中，点A，B，E在同一条直线上，P是线段CF的中点，连接PD，PG．‎ ‎（1）若∠BAD=∠AEF=120°，请直接写出∠DPG的度数及的值．‎ ‎（2）若∠BAD=∠AEF=120°，将菱形ABCD绕点A顺时针旋转，使菱形ABCD的对角线AC恰好与菱形AEFG的边AE在同一直线上，如图2，此时，（1）中的两个结论是否发生改变？写出你的猜想并加以说明．‎ ‎（3）若∠BAD=∠AEF=180°﹣2α（0°＜α＜90°），将菱形ABCD绕点A顺时针旋转到图3的位置，求出的值．‎ ‎　‎ 三角形综合题答案 ‎1．已知，如图，Rt△ABC中，∠ACB=90°，BC=8，cot∠BAC=，点D在边BC上（不与点B、C重合），点E在边BC的延长线上，∠DAE=∠BAC，点F在线段AE上，∠ACF=∠B．设BD=x．‎ ‎（1）若点F恰好是AE的中点，求线段BD的长；‎ ‎（2）若y=，求y关于x的函数关系式，并写出它的定义域；‎ ‎（3）当△ADE是以AD为腰的等腰三角形时，求线段BD的长．‎ 解：（1）在Rt△ABC中，∠ACB=90°，BC=8，‎ ‎ cot∠BAC=，‎ ‎ ∴AC=6，AB=10，‎ ‎∵∠DAE=∠BAC，‎ ‎∴∠FAC=∠DAB，‎ ‎∵∠ACF=∠B，‎ ‎∴△ABD∽△ACF，‎ ‎∴，‎ 在Rt△ABC中，点F恰好是AE的中点，‎ ‎∴CF=AE=AF，‎ ‎∴AD=BD，‎ 在Rt△ACD中，AC=6，CD=BC﹣BD=BC﹣AD=8﹣AD，‎ 根据勾股定理得，AC2+CD2=AD2，‎ ‎∴36+（8﹣AD）2=AD2，‎ ‎∴AD=，‎ ‎∴BD=AD=，‎ ‎（2）如图1，过点F作FM⊥AC于M，‎ 由（1）知，∴=，‎ ‎∴CF==×x=x，‎ 由（1）△ABD∽△ACF，‎ ‎∴∠B=∠ACF，‎ ‎∴tan∠ACF=tanB===，‎ ‎∴MC=x，‎ ‎∴y===（0＜x＜8）‎ ‎（3）∵△ADE是以AD为腰的等腰三角形，‎ ‎∴①当AD=AE时，‎ ‎∴∠AED=∠ADE，‎ ‎∵∠ACD=90°，‎ ‎∴∠EAC=∠DAC=∠DAB，‎ ‎∴AD是∠BAC的平分线，‎ ‎∴，‎ ‎∵AC=6，AB=10，CD=8﹣BD，‎ ‎∴，‎ ‎∴BD=5，‎ 当AD=DE时，‎ ‎∴∠DAE=∠DEA=∠BAC，‎ ‎∴∠ADE=2∠B，‎ ‎∴∠B=∠DAB，‎ ‎∴AD=BD=（是（1）的那种情况）．‎ 即：BD=5或BD=时，△ADE是以AD为腰的等腰三角形．‎ ‎2．如图，△ABC边AB上点D、E（不与点A、B重合），满足∠DCE=∠ABC，∠ACB=90°，AC=3，BC=4；‎ ‎（1）当CD⊥AB时，求线段BE的长；‎ ‎（2）当△CDE是等腰三角形时，求线段AD的长；‎ ‎（3）设AD=x，BE=y，求y关于x的函数解析式，并写出定义域．‎ ‎（1）‎ 在△ABC中，∠ACB=90°，AC=3，BC=4，‎ ‎∴AB=5，sinA=，tanB=，‎ 如图，当CD⊥AB时，△ACD为直角三角形，‎ ‎∴CD=AC•sinA=，‎ ‎∴AD==，‎ 又∵∠DCE=∠ABC，‎ ‎∴在Rt△CDE中，DE=CD•tan∠DCE=×=，‎ ‎∴BE=AB﹣AD﹣DE=5﹣﹣=；‎ ‎（2）当△CDE时等腰三角形时，可知∠CDE＞∠A＞∠B=∠DCE，∠CED＞∠B=∠DCE，‎ ‎∴唯有∠CED=∠CDE，‎ 又∵∠B=∠DCE，∠CDE=∠BDC，‎ ‎∴∠BCD=∠CED=∠CDE=∠BDC，‎ ‎∴BD=BC=4，‎ ‎∴AD=5﹣4=1；‎ ‎（3）如图所示，作CH⊥AB于H，‎ ‎∵×BC×AC=AB×CH，‎ ‎∴CH=，‎ ‎∴Rt△ACH中，AH==，‎ ‎∴在Rt△CDH中，CD2=CH2+DH2=（）2+（﹣x）2=x2﹣x+9，‎ 又∵∠CDE=∠BDC，∠DCE=∠B，‎ ‎∴△BDC∽△CDE，‎ ‎∴CD2=DE•DB，‎ 即x2﹣x+9=（5﹣x﹣y）（5﹣x），‎ 解得．‎ 3． 如图，已知△ABC中，AB=AC=3，BC=2，点D是边AB上的动点，过点D作DE∥BC，交边AC于点E，点Q是线段DE上的点，且QE=2DQ，连接BQ并延长，交边AC于点P．设BD=x，AP=y．‎ ‎（1）求y关于x的函数解析式及定义域；‎ ‎（2）当△PQE是等腰三角形时，求BD的长；‎ ‎（3）连接CQ，当∠CQB和∠CBD互补时，求x的值．‎ 解：（1）如图所示，过点D作DF∥AC，交BP于F，则 根据QE=2DQ，可得 ‎==，‎ 又∵DE∥BC，‎ ‎∴==1，‎ ‎∴EC=BD=x，PE=3﹣x﹣y，DF=，‎ ‎∵DF∥AC，‎ ‎∴=，即=，‎ ‎∴y=，定义域为：0＜x＜3；‎ ‎（2）‎ ‎∵DE∥BC，‎ ‎∴△PEQ∽△PBC，‎ ‎∴当△PEQ为等腰三角形时，△PBC也为等腰三角形，‎ ‎①当PB=BC时，△ABC∽△BPC，‎ ‎∴BC2=CP•AC，即4=3（3﹣y），‎ 解得y=，‎ ‎∴=，‎ 解得x==BD；‎ ‎②当PC=BC=2时，AP=y=1，‎ ‎∴=1，‎ 解得x==BD；‎ ‎③当PC=PB时，点P与点A重合，不合题意；‎ ‎（3）∵DE∥BC，‎ ‎∴∠BDQ+∠CBD=180°，‎ 又∵∠CQB和∠CBD互补，‎ ‎∴∠CQB+∠CBD=180°，‎ ‎∴∠CQB=∠BDQ，‎ ‎∵BD=CE，‎ ‎∴四边形BCED是等腰梯形，‎ ‎∴∠BDE=∠CED，‎ ‎∴∠CQB=∠CED，‎ 又∵∠DQB+∠CQB=∠ECQ+∠CED，‎ ‎∴∠DQB=∠ECQ，‎ ‎∴△BDQ∽△QEC，‎ ‎∴=，即2DQ2=x2，‎ ‎∴DQ=，DE=，‎ ‎∵DE∥BC，‎ ‎∴=，即=，‎ 解得x=．‎ ‎4．如图，在Rt△ABC中，∠ACB=90°，=，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F．‎ ‎（1）探究发现：‎ 如图1，若m=n，点E在线段AC上，则=　1　；‎ ‎（2）数学思考：‎ ‎①如图2，若点E在线段AC上，则=　　（用含m，n的代数式表示）；‎ ‎②当点E在直线AC上运动时，①中的结论是否任然成立？请仅就图3的情形给出证明；‎ ‎（3）拓展应用：若AC=，BC=2，DF=4，请直接写出CE的长．‎ 解：（1）当m=n时，即：BC=AC，‎ ‎∵∠ACB=90°，‎ ‎∴∠A+∠ABC=90°，‎ ‎∵CD⊥AB，‎ ‎∴∠DCB+∠ABC=90°，‎ ‎∴∠A=∠DCB，‎ ‎∵∠FDE=∠ADC=90°，‎ ‎∴∠FDE﹣∠CDE=∠ADC﹣∠CDE，‎ 即∠ADE=∠CDF，‎ ‎∴△ADE∽△CDF，‎ ‎∴，‎ ‎∵∠A=∠DCB，∠ADC=∠BDC=90°，‎ ‎∴△ADC∽△CDB，‎ ‎∴=1，‎ ‎∴=1‎ ‎（2）①∵∠ACB=90°，‎ ‎∴∠A+∠ABC=90°，‎ ‎∵CD⊥AB，‎ ‎∴∠DCB+∠ABC=90°，‎ ‎∴∠A=∠DCB，‎ ‎∵∠FDE=∠ADC=90°，‎ ‎∴∠FDE﹣∠CDE=∠ADC﹣∠CDE，‎ 即∠ADE=∠CDF，‎ ‎∴△ADE∽△CDF，‎ ‎∴，‎ ‎∵∠A=∠DCB，∠ADC=∠BDC=90°，‎ ‎∴△ADC∽△CDB，‎ ‎∴，‎ ‎∴‎ ‎②成立．如图，‎ ‎∵∠ACB=90°，‎ ‎∴∠A+∠ABC=90°，‎ 又∵CD⊥AB，‎ ‎∴∠DCB+∠ABC=90°，‎ ‎∴∠A=∠DCB，‎ ‎∵∠FDE=∠ADC=90°，‎ ‎∴∠FDE+∠CDE=∠ADC+∠CDE，‎ 即∠ADE=∠CDF，‎ ‎∴△ADE∽△CDF，‎ ‎∴，‎ ‎∵∠A=∠DCB，∠ADC=∠BDC=90°，‎ ‎∴△ADC∽△CDB，‎ ‎∴，‎ ‎∴．‎ ‎（3）由（2）有，△ADE∽△CDF，‎ ‎∵=，‎ ‎∴=，‎ ‎∴CF=2AE，‎ 在RtDEF中，DE=2，DF=4，‎ ‎∴EF=2，‎ ‎①在Rt△CEF中，CF=2AE=2（AC﹣CE）=2（﹣CE），EF=2，‎ 根据勾股定理得，CE2+CF2=EF2，‎ ‎∴CE2+[2（﹣CE）]2=40‎ ‎∴CE=2，或CE=﹣（舍）‎ ‎②在Rt△CEF中，CF=2AE=2（AC+CE）=2（+CE），EF=2，‎ 根据勾股定理得，CE2+CF2=EF2，‎ ‎∴CE2+[2（+CE）]2=40，‎ ‎∴CE=，或CE=﹣2（舍），‎ 即：CE=2或CE=．‎ ‎5．如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）‎ ‎（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD　=　∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是　BD=CD+AD　；‎ ‎（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=AD；‎ ‎（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）‎ 解：（1）如图2，‎ ‎∵∠CDP=120°，‎ ‎∴∠CDB=60°，‎ ‎∵∠BAC=60°，‎ ‎∴∠CDB=∠BAC=60°，‎ ‎∴A、B、C、D四点共圆，‎ ‎∴∠ACD=∠ABD．‎ 在BP上截取BE=CD，连接AE．‎ 在△DCA与△EBA中，‎ ‎，‎ ‎∴△DCA≌△EBA（SAS），‎ ‎∴AD=AE，∠DAC=∠EAB，‎ ‎∵∠CAB=∠CAE+∠EAB=60°，‎ ‎∴∠DAE=60°，‎ ‎∴△ADE是等边三角形，‎ ‎∴DE=AD．‎ ‎∵BD=BE+DE，‎ ‎∴BD=CD+AD．‎ 故答案为=，BD=CD+AD；‎ ‎（2）如图3，设AC与BD相交于点O，在BP上截取BE=CD，连接AE，过A作AF⊥BD于F．‎ ‎∵∠CDP=60°，‎ ‎∴∠CDB=120°．‎ ‎∵∠CAB=120°，‎ ‎∴∠CDB=∠CAB，‎ ‎∵∠DOC=∠AOB，‎ ‎∴△DOC∽△AOB，‎ ‎∴∠DCA=∠EBA．‎ 在△DCA与△EBA中，‎ ‎，‎ ‎∴△DCA≌△EBA（SAS），‎ ‎∴AD=AE，∠DAC=∠EAB．‎ ‎∵∠CAB=∠CAE+∠EAB=120°，‎ ‎∴∠DAE=120°，‎ ‎∴∠ADE=∠AED==30°．‎ ‎∵在Rt△ADF中，∠ADF=30°，‎ ‎∴DF=AD，‎ ‎∴DE=2DF=AD，‎ ‎∴BD=DE+BE=AD+CD，‎ ‎∴BD﹣CD=AD；‎ ‎（3）线段BD、CD与AD之间的数量关系为BD+CD=AD或CD﹣BD=AD．‎ ‎6．已知，在△ABC中，∠ACB=90°，CA=CD，CG⊥AD于点H，交AB于点G，E为AB上一点，连接CE交AD于点F．‎ ‎（1）如图1，若CE⊥AB于点E，HG=1，CH=5，求CF的长；‎ ‎（2）如图2，若AC=AE，∠GEH=∠ECH，求证：CE=HE；‎ ‎（3）如图3，若E为AB的中点，作A关于CE的对称点A′，连接CA′，EA′，DA′，请直接写出∠CEH，∠A′CD，∠EA′D之间的等量关系．‎ 解：（1）∵∠ACB=90°，CA=CD，‎ ‎∴△ACD是等腰直角三角形，‎ ‎∴∠CAD=∠CDA=45°，‎ ‎∵CG⊥AD，‎ ‎∴∠CHF=∠AHG=90°，∠ACH=∠DCH=∠ACB=×90°=45°，AH=DH=CH=5，‎ ‎∴∠GAH+∠AGC=90°，‎ ‎∵CE⊥AB，‎ ‎∴∠CEG=90°，‎ ‎∴∠GCE+∠AGC=90°，‎ ‎∴∠GCE=∠GAH，‎ 在△CHF与△AHG中，，‎ ‎∴△CHF≌△AHG，‎ ‎∴HF=HG=1，‎ ‎∴CF===；‎ ‎（2）如图2，过H作MH⊥EH，交CE于M，连接AM，‎ ‎∵AC=AE，‎ ‎∴∠AEC=∠ACE，‎ ‎∵∠GEH=∠ECG，‎ ‎∵MH⊥EH，‎ ‎∴△EHM为等腰直角三角形，∠EHM=90°，‎ ‎∴EH=MH，EM=HE，‎ ‎∴∠AHM=∠AHC+∠CHM=90°+∠CHM=∠EHM+∠CHM=∠CHE，‎ 在△AHM与△CHE中，，‎ ‎∴△AHM≌△CHE，‎ ‎∴∠MAF=∠ECH，‎ ‎∴∠MAF+∠AFC=∠ECH+∠AFC=180°，‎ ‎∴∠CHD=180°﹣90°，‎ ‎∴AM⊥CE，‎ ‎∵AC=AE，‎ ‎∴△ACE是等腰三角形，‎ ‎∴CM=EM=HE，‎ ‎∴CE=2EM=2HE；‎ ‎（3）∵H为AD的中点，E我AB的中点，‎ ‎∴EH是△ABD的中位线，‎ ‎∴EH∥BC，‎ ‎∴∠CEH=∠BCE，‎ ‎∴∠ACE=∠ACB﹣∠BCE=90°﹣∠BCE=90°﹣∠CEH，‎ ‎∵EC=AE，‎ ‎∴∠CAE=∠ACE=90°﹣∠CEH，‎ ‎∴∠CAE=∠ACE=90°﹣∠CEH，‎ ‎∵A关于CE的对称点A′，‎ ‎∴∠CA′E=∠CAE=90°﹣∠CEH，CA=CA′，‎ ‎∵CA=CD，‎ ‎∴CA′=CD，‎ ‎∴∠CDA′=∠CA′D=∠CA′E+∠EA′D=90°﹣∠CEH+∠EA′D，‎ ‎∵∠A′CD+∠CDA′+∠CA′D=180°，‎ ‎∴∠A′CD+90°﹣∠CEH+∠EA′D+90°﹣∠CEH+∠EA′D=180°，‎ 化简得：∠A′CD+2∠EA′D=2∠CEH，‎ ‎7．（1）问题发现 如图1，在Rt△ABC中，∠A=90°，=1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD．‎ 填空：①=　1　；②∠ACD的度数为　45°　．‎ ‎（2）拓展探究 如图2，在Rt△ABC中，∠A=90°，=k．点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B的数量关系以及PB与CD之间的数量关系，并说明理由．‎ ‎（3）解决问题 如图3，在△ABC中，∠B=45°，AB=4，BC=12，P是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD．若PA=5，请直接写出CD的长．‎ 解：（1）∵∠A=90°，=1，‎ ‎∴AB=AC，‎ ‎∴∠B=45°，‎ ‎∵∠PAD=90°，∠APD=∠B=45°，‎ ‎∴AP=AD，‎ ‎∴∠BAP=∠CAD，‎ 在△ABP与△ACD中，，‎ ‎∴△ABP≌△ACD，‎ ‎∴PB=CD，∠ACD=∠B=45°，‎ ‎∴=1，‎ 故答案为：1，45°；‎ ‎（2）∠ACD=∠B，==k；‎ ‎∵∠BAC=∠PAD=90°，∠B=∠APD，‎ ‎∴△ABC∽△APD，‎ ‎∴=k，‎ ‎∵∠BAP+∠PAC=∠PAC+∠CAD=90°，‎ ‎∴∠BAP=∠CAD，‎ ‎∴△ABP∽△CAD，‎ ‎∴∠ACD=∠B，==k；‎ ‎（3）过A作AH⊥BC于H，‎ ‎∵∠B=45°，‎ ‎∴△ABH是等腰直角三角形，‎ ‎∵AB=4，‎ ‎∴AH=BH=4，‎ ‎∵BC=12，‎ ‎∴CH=8，‎ ‎∴AC==4，‎ ‎∴PH==3，‎ ‎∴PB=1，‎ ‎∵∠BAC=∠PAD=，∠B=∠APD，‎ ‎∴△ABC∽△APD，‎ ‎∴，‎ ‎∵∠BAP+∠PAC=∠PAC+∠CAD，‎ ‎∴∠BAP=∠CAD，‎ ‎∴△ABP∽△CAD，‎ ‎∴=，即，‎ ‎∴CD=．‎ ‎8．Rt△ABC与Rt△DEF的位置如图所示，其中AC=2，BC=6，DE=3，∠D=30°，其中，Rt△DEF沿射线CB以每秒1个单位长度的速度向右运动，射线DE、DF与射线AB分别交于N、M两点，运动时间为t，当点E运动到与点B重合时停止运动．‎ ‎（1）当Rt△DEF在起始时，求∠AMF的度数；‎ ‎（2）设BC的中点的为P，当△PBM为等腰三角形时，求t的值；‎ ‎（3）若两个三角形重叠部分的面积为S，写出S与t的函数关系式和相应的自变量的取值范围．‎ 解：（1）‎ 在Rt△ABC中，tan∠B===，‎ ‎∴∠B=30°，‎ 在Rt△DEF中，∠D=30°，‎ ‎∴∠DFC=60°，‎ ‎∴∠FMB=∠DFC﹣∠B=30°，‎ ‎∴∠AMF=180°﹣∠FMB=150°；‎ ‎（2）∵BC=6，点P为线段BC的中点，‎ ‎∴BP=3，‎ ‎（ⅰ）若点M在线段AB上，‎ ‎①当PB=PM时，PB=PM=3，‎ ‎∵DE=3，∠D=30°，‎ ‎∴EF=DE•tan30°=3，‎ ‎∴此时t=0；‎ ‎②如右图（1）所示 当BP=BM时，BP=BM=3，‎ ‎∵∠B=30°，∠DFE=60°，‎ ‎∴∠FMB=30°，‎ ‎∴△BMF为等腰三角形．‎ 过点F作FH⊥MB于H，则BH=BM=，‎ ‎ 在Rt△BHF中，∠B=30°，‎ ‎∴BF=，‎ ‎∴t=3﹣；‎ ‎③如右图（2）所示，‎ 当MP=MB时，∠MPB=∠B=30‎ ‎∵∠MFP=60°，‎ ‎∴PM⊥MF，∠BMF=30°‎ ‎∴FB=FM，‎ 设FB=x，则FM=x，PF=2x．‎ ‎∴3x=3，x=1‎ ‎∴t=2；‎ ‎（ⅱ）若点M在射线AB上，‎ 如右图（3）所示，‎ ‎∵∠PBM=150°‎ ‎∴当△PBM为等腰三角形时，有BP=BM=3‎ ‎∵△BFM为等腰三角形，‎ ‎∴过点F作FH⊥BM于H，则BH=BM=，‎ 在Rt△BHF中，∠FBH=30°‎ ‎∴BF=，‎ ‎∴t=3+，‎ 综上所述，t的值为0，3﹣，2，3+．‎ ‎（3）当0＜t≤3时，BE=6﹣t，NE=（6﹣t），‎ ‎∴=，‎ 过点F作FH⊥MB于H，如右图（1）所示，‎ ‎∵FB=3﹣t ‎∴HF=（3﹣t），HB=（3﹣t），MB=（3﹣t），‎ ‎∴=，‎ ‎∴S=S△BEN﹣S△BMF==，‎ 当3＜t≤6时，BE=6﹣t，NE=（6﹣t），如右图（4）所示，‎ ‎∴S==，‎ 由上可得，当0＜t≤3时，S=，‎ 当3＜t≤6时，S=，‎ 即S=．‎ ‎9．如图，已知等腰△ABC中，AC=BC，点D、E、F分别是线段AC、BC、AD的中点，连接FE、ED，BF的延长线交ED的延长线于点G，连接GC．‎ ‎（1）求证：EF∥CG；‎ ‎（2）若AC=AB，求证：AC=CG；‎ ‎（3）如图2，若CG=EG，则=　　．‎ ‎（1）证明：∵点D、E分别是线段AC、BC的中点，‎ ‎∴DE为△ABC的中位线，‎ ‎∴DE∥AB，‎ ‎∴∠CDE=∠A．‎ ‎∵∠CDE=FDG，‎ ‎∴∠FDG=∠A．‎ ‎∵点F为线段AD的中点，‎ ‎∴AF=DF．‎ 在△ABF和△DGF中，，‎ ‎∴△ABF≌△DGF（ASA），‎ ‎∴BF=GF，‎ ‎∴点F为线段BG的中点，‎ ‎∵点E为线段BC的中点，‎ ‎∴EF为△BCG的中位线，‎ ‎∴EF∥CG．‎ ‎（2）证明：在图1中，过点C作CM⊥AB于点M．‎ ‎∵AC=BC，‎ ‎∴AM=BM=AB．‎ ‎∵AC=AB，‎ ‎∴==．‎ ‎∵AF=AD=AC=AB，‎ ‎∴==，‎ ‎∴△BAF∽△CAM，‎ ‎∴∠AFB=∠AMC=90°，‎ ‎∴CF⊥BG．‎ ‎∵点F为线段BG的中点，‎ ‎∴BC=CG，‎ 又∵AC=BC，‎ ‎∴AC=CG．‎ （3） 解：‎ ‎∵DE为△ABC的中位线，‎ ‎∴DE=AB，CE=BC=AC，‎ ‎∵DG=AB，EG=DE+DG，‎ ‎∴EG=AB．‎ ‎∵DE∥AB，‎ ‎∴∠GEC=∠CBA，‎ ‎∵AC=BC，CG=EG，‎ ‎∴△GEC∽△CBA，‎ ‎∴，既，‎ ‎∴=，‎ 故答案为：．‎ ‎10．在Rt△ABC中，∠CAB=90°，AC=AB=6，D，E分别是AB，AC的中点，若等腰Rt△ADE绕点A逆时针旋转，得到Rt△AD1E1，设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．‎ ‎（1）如图1，当α=90°时，线段BD1的长等于　3　，线段CE1的长等于　3　；‎ ‎（2）如图2，当α=135°时，设直线BD1与CA的交点为F，求证：BD1=CE1，且BD1⊥CE1；‎ ‎（3）点P到AB所在直线的距离的最大值是　　．‎ 解：‎ ‎（1）∵∠CAB=90°，AC=AB=6，D，E分别是边AB，AC的中点，‎ ‎∴AE=AD=3，‎ ‎∵等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0＜α≤180°），‎ ‎∴当α=90°时，AE1=3，∠E1AE=90°，‎ ‎∴BD1==3，E1C==3；‎ 故答案为：3，3；‎ ‎（2）证明：当α=135°时，如图2，连接CE1，‎ ‎∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到，‎ ‎∴AD1=AE1，∠D1AB=∠E1AC=135°，‎ 在△D1AB和△E1AC中 ‎，‎ ‎∴△D1AB≌△E1AC（SAS），‎ ‎∴BD1=CE1，且∠D1BA=∠E1CA，‎ 记直线BD1与AC交于点F，‎ ‎∴∠BFA=∠CFP，‎ ‎∴∠CPF=∠FAB=90°，‎ ‎∴BD1⊥CE1；‎ ‎（3）解：如图3，作PG⊥AB，交AB所在直线于点G，‎ ‎∵D1，E1在以A为圆心，AD为半径的圆上，‎ ‎∴当BD1所在直线与⊙A相切时，直线BD1与CE1的交点P到直线AB的距离最大，‎ 此时四边形AD1PE1是正方形，PD1=3，则BD1==3，‎ 故∠ABP=30°，‎ 则PB=3+3，‎ 故点P到AB所在直线的距离的最大值为：PG=，‎ 故答案为：．‎ ‎11．如图，在Rt△ABC中，∠ACB=90°，点D为边BC上任意一点，以直线AD为对称轴，作Rt△ABC的轴对称图形Rt△AEF，点M、点N、点P、点Q分别为AB、BC、EF、EA的中点．‎ ‎（1）求证：MN=PQ；‎ ‎（2）如图2，当BD=时，判断点M、点N、点P、点Q围成的四边形的形状，并说明理由；‎ ‎（3）若BC=6，请你直接写出当①BD=3；②BD=6时，点M、点N、点P、点Q围成图形的形状．‎ 解：（1）∵△ABC与△AEF关于直线AD对称，如图1，‎ ‎∴△ABC≌△AEF，‎ ‎∴AC=AF，‎ ‎∵点M、N、P、Q分别是AB、BC、EF、EA的中点，‎ ‎∴MN、PQ分别是△ABC和△AEF的中位线，‎ ‎∴MN=AC，PQ=AF，‎ ‎∴MN=PQ；‎ ‎（2）当BD=BC时，点M、点N、点P、点Q围成的四边形是矩形．‎ 连结BE、MN、PQ，如图2，‎ ‎∵点M、点Q是AB、AE的中点．‎ ‎∴MQ∥BE且MQ=BE，‎ ‎∵点N是BC中点，‎ ‎∴BN=BC，‎ 又∵BD=BC，‎ ‎∴DN=BN﹣BD=BC﹣BC=BC，‎ ‎∴‎ ‎∵点B与点E关于直线AD对称，‎ ‎∴BE⊥AD，‎ 同理PN⊥AD，‎ ‎∴BE∥PN，‎ ‎∴△PDN∽△EDB，‎ ‎∴‎ ‎∴PN∥BE，PN=BE，‎ ‎∴MQ∥PN且MQ=PN，‎ ‎∴四边形MQNP是平行四边形，‎ ‎∵MN=PQ，‎ ‎∴四边形MQNP是矩形．‎ ‎（3）当BD=3时，围成等腰三角形；‎ 当BD=6时，围成矩形．‎ ‎12．在Rt△ABC中，∠ACB=90°，点D在AB边上，AD=BD，过点D作射线DH，交BC边于点M．‎ ‎（1）如图1，若∠B=30°，求证：△ACD是等边三角形；‎ ‎（2）如图2，若AC=10，AD=13，∠CDH=∠A．‎ ‎①求线段DM的长；‎ ‎②点P是射线DH上一点，连接AP交CD于点N，当△DMN是等腰三角形时，求线段MP的长．‎ ‎（1）证明：∵∠B=30°，∠ACB=90°，‎ ‎∴∠A=60°，‎ 由题意可得D是直角三角形斜边A边上的中点，‎ ‎∴CD=AD，‎ ‎∴∠ACD=∠A=60°，‎ ‎∴∠ADC=60°，‎ ‎∴△ACD为等边三角形；‎ ‎（2）解：①∵点D是直角三角形斜边AB上的中点，‎ ‎∴AC=CD=AD，‎ ‎∴∠ACD=∠A，‎ ‎∵∠CDH=∠A，‎ ‎∴∠ACD=∠CDH，‎ ‎∴DH∥AC，‎ ‎∴DM为△ABC的中位线，‎ ‎∴DM=AC=5；‎ ‎②分三种情况考虑：‎ ‎（i）当MN=DN时，如图1所示，‎ 由①得：AD=CD，∠A=∠ACD=∠CDH，DM=5，‎ ‎∵MN=DN，‎ ‎∴∠CDN=∠DMN=∠A=∠ACD，‎ ‎∴△ADC∽△DNM，‎ ‎∴=，即=，‎ 解得：DN==CD，‎ ‎∴CN=DN，‎ ‎∵DH∥AC，‎ ‎∴△ACN≌△PDN，‎ ‎∴PD=AC=10，‎ ‎∴MP=PD﹣DM=10﹣5=5；‎ ‎（ii）当MN=DM=5时，如图2所示，则有∠MND=∠MDN=∠ACD=∠A，‎ ‎∴△ADC∽△MDN，‎ ‎∴=，即=，‎ 解得：DN=，‎ ‎∴CN=13﹣=，‎ ‎∵△ACN∽△PDN，‎ ‎∴=，即=，‎ 解得：PD=，‎ 则MP=DM﹣PD=5﹣=；‎ ‎（iii）当DN=DM时，如图2所示，则有DN=5，CN=13﹣5=8，‎ ‎∵△ACN∽△PDN，‎ ‎∴=，即=，‎ 解得：PD=，‎ 则MP=PD﹣DM=．‎ ‎13．等腰三角形ABC中，AB=CB，BO⊥AC，点P为射线BC上的动点（不与点B重合），在射线CA上截取CD=CB，作PF⊥BD，分别交射线BO，BD于点E，F．设∠ABC=α．‎ ‎（1）令∠ABC=90°．‎ ‎①如图1，当点P与点C重合时，求证：△BOD≌△POE；‎ ‎②如图2，当点P在点C的左边时，求的值；‎ ‎③猜想：当点P在点C的右边时，的值又是多少？‎ 请直接写出．‎ ‎（2）设点P在点C的右边，请在图3（∠ABC＞90°）或图4（∠ABC＜90°）中继续探究的值（用含α的式子表示），并说明理由．‎ 解：（1）①如图1中，‎ ‎∵AB=BC，∠ABC=90°，BO⊥AC，‎ ‎∴OA=OC=OB，∠BOC=90°，‎ ‎∵CF⊥BD，‎ ‎∴∠CFD=90°，‎ ‎∵∠CDF+∠DCF=90°，∠DCF+∠CEO=90°，‎ ‎∴∠CEO=∠BDO，‎ 在△BOD和△COE中，‎ ‎，‎ ‎∴△BOD≌△COE，（即△BOD≌△POE）．‎ ‎②如图2中，作PM⊥OB于M，交BD于N．‎ ‎∵PM⊥OB，AC⊥OB，‎ ‎∴PN∥AC，‎ ‎∴∠PNB=∠CDB，∠NPB=∠C=45°，‎ ‎∵CB=DC，‎ ‎∴∠CBD=∠CDB=∠PNB，‎ ‎∴PB=PN，∵PF⊥BN，‎ ‎∴BF=FN，‎ ‎∵∠MPB=∠MBP=45°，‎ ‎∴BM=PM，‎ ‎∵∠FEB=∠MEP，∠EFB=∠PME=90°，‎ ‎∴∠EBF=∠EPM，‎ 在△BMN和△PME中，‎ ‎，‎ ‎∴△BMN≌△PME，‎ ‎∴BN=PE，‎ ‎∵BF=FN，‎ ‎∴=．‎ ‎③如图3中，当点P在点C的右边时，的值为．‎ 理由：作PM⊥OB于M，交BD于N．‎ ‎∵PM⊥OB，AC⊥OB，‎ ‎∴PN∥AC，‎ ‎∴∠PNB=∠CDB，∠NPB=∠ACB=45°，‎ ‎∵CB=DC，‎ ‎∴∠CBD=∠CDB=∠PNB，‎ ‎∴PB=PN，∵PF⊥BN，‎ ‎∴BF=FN，‎ ‎∵∠MPB=∠MBP=45°，‎ ‎∴BM=PM，‎ ‎∵∠FEB=∠MEP，∠EFB=∠PME=90°，‎ ‎∴∠EBF=∠EPM，‎ 在△BMN和△PME中，‎ ‎，‎ ‎∴△BMN≌△PME，‎ ‎∴BN=PE，‎ ‎∵BF=FN，‎ ‎∴=．‎ ‎（2）如图4中，=．‎ 理由：作PM⊥BO于M，交BD于N．‎ ‎∵PM⊥OB，AC⊥OB，‎ ‎∴PN∥AC，‎ ‎∴∠PNB=∠CDB，∠NPB=∠ACB=，‎ ‎∵CB=DC，‎ ‎∴∠CBD=∠CDB=∠PNB，‎ ‎∴PB=PN，∵PF⊥BN，‎ ‎∴BF=FN，‎ ‎∵∠FEB=∠MEP，∠EFB=∠PME=90°，‎ ‎∴∠EBF=∠EPM，‎ ‎∴△BMN∽△PME，‎ ‎∴==tan∠BPM，‎ ‎∴BPM，‎ ‎∴=．‎ 如图5中，=．‎ 理由：理由：作PM⊥BO于M，交BD于N．‎ ‎∵PM⊥OB，AC⊥OB，‎ ‎∴PN∥AC，‎ ‎∴∠PNB=∠CDB，∠NPB=∠ACB=，‎ ‎∵CB=DC，‎ ‎∴∠CBD=∠CDB=∠PNB，‎ ‎∴PB=PN，∵PF⊥BN，‎ ‎∴BF=FN，‎ ‎∵∠FEB=∠MEP，∠EFB=∠PME=90°，‎ ‎∴∠EBF=∠EPM，‎ ‎∴△BMN∽△PME，‎ ‎∴==tan∠BPM，‎ ‎∴BPM，‎ ‎∴=．‎ ‎14．如图1，△ABC中，∠BAC=90°，AB=AC，AD⊥BC于点D，点E在AC边上，连接BE．‎ ‎（1）若AF是△ABE的中线，且AF=5，AE=6，连接DF，求DF的长；‎ ‎（2）若AF是△ABE的高，延长AF交BC于点G．‎ ‎①如图2，若点E是AC的中点，连接EG，求证：AG+EG=BE；‎ ‎②如图3，若点E是AC边上的动点，连接DF．当点E在AC边上（不含端点）运动时，∠DFG的大小是否改变，如果不变，请求出∠DFG的度数；如果要变，请说明理由．‎ 解：（1）在Rt△ABE中，AF是中线，‎ ‎∴AF=BE，‎ ‎∵AF=5，‎ ‎∴BE=10，‎ 在Rt△ABE中，AE=6，BE=10，可求得AB=8，‎ 又∵AB=AC，∴AC=8，‎ ‎∴CE=AC﹣AE=2，‎ ‎∵AB=AC，AD⊥BC，‎ ‎∴BD=DC，‎ 又∵点F是BE的中点，‎ ‎∴DF=CE=1；‎ ‎（2）如图1，过点C作CM⊥AC，交AG的延长线于点M，则∠ACM=90°，‎ 又∵∠BAC=90°，‎ ‎∴∠BAC=∠ACM，‎ ‎∵AF是△ABE的高，‎ ‎∴∠AFB=90°，‎ ‎∴∠1+∠BAF=90°，‎ ‎∵∠BAC=90°，‎ ‎∴∠2+∠BAF=90°，‎ ‎∴∠1=∠2，‎ 在△ABE和△CAM中 ‎∴△ABE≌△CAM（ASA），‎ ‎∴AE=CM，BE=AM，‎ 又点E是AC边的中点，‎ ‎∴CE=AE=CM，‎ ‎∵AB=AC，∠BAC=90°，‎ ‎∴∠ABC=∠ACB=45°，‎ 又∵∠ACM=90°，‎ ‎∴∠MCG=45°=∠ACB，‎ 在△CEG和△CMG中 ‎∴△CEG≌△CMG（SAS），‎ ‎∴EG=GM，‎ 又BE=AM，‎ ‎∴AG+EG=AG+GM=AM=BE；‎ ‎（3）如图2，过点D作DN⊥DF，交AG的延长线于点N，则∠NDF=90°，‎ ‎∵AD⊥BC，‎ ‎∴∠ADB=90°=∠NDF，‎ ‎∴∠ADB+∠ADF=∠NDF+∠ADF，即∠BDF=∠ADN，‎ ‎∵∠ADB=∠AFB=90°，∠5=∠6，‎ ‎∴∠3=∠4，‎ 在Rt△ABC中，BD=DC，‎ ‎∴AD=BC=BD，‎ 在△BDF和△ADN中 ‎，‎ ‎∴△BDF≌△ADN（ASA），‎ ‎∴DF=DN，‎ 又∠NDF=90°，‎ ‎∴∠DFN=∠DNF=45°，‎ 即∠DFG=45°．‎ ‎15．在△ABC中，AD、AE分别是△ABC的内、外角平分线．‎ ‎（1）如图①，CG⊥AD于G，BG的延长线交AE于H，求证：AH=EH；‎ ‎（2）如图①，在（1）的条件下，若AE=2AD，BE=5BC，则tan∠AHB=　　；‎ ‎（3）如图②，点M是DE的中点，BE=5BC=10，求MD的长．‎ 证明：（1）如图1，延长CG交AB于M，‎ ‎∵AD平分∠BAC，CG⊥AD，‎ ‎∴CG=MG．‎ ‎∵AD、AE分别是△ABC的内、外角平分线，‎ ‎∴∠HAG=90°，‎ ‎∴AE∥CG，‎ ‎∵==，‎ ‎∴AH=EH．‎ ‎（2）由角平分线定理得=．‎ ‎∵AC=AM，‎ ‎∴=．‎ 又=，BE=5BC，‎ ‎∴==，‎ ‎∴=．‎ 设CD=4，DB=5，‎ 则EC=36，‎ ‎∴==，‎ ‎∵AH=EH，AE=2AD，‎ ‎∴AH=AD，‎ ‎∴tan∠AHB==；‎ 故答案是：；‎ ‎（3）由（2）可知：BE=45a=10，a=．‎ ‎∴MD=20a=．‎ ‎16．如图，△ABC是等边三角形，AB=2，D是边BC的中点，点P从点A出发，沿AB﹣BD以每秒1个单位长度的速度向终点D运动．同时点Q从点C出发，沿CA﹣AC以每秒1个单位长度的速度运动．当点P停止运动时，点Q也随之停止运动，设点P的运动时间为t（秒），△PQD的面积为S．‎ ‎（1）求线段PB的长（用含t的代数式）．‎ ‎（2）当△PQD是等边三角形时，求t的值．‎ ‎（3）当S＞0时，求S与t的函数关系式．‎ ‎（4）若点D关于直线PQ的对称点为点D′，且S＞0，直接写出点D′落在△ABC的边上时t的值．‎ 解：（1）∵△ABC是等边三角形，AB=2，‎ ‎∴当0≤t≤2时，BP=2﹣t；‎ 当2≤t≤3时，BP=t﹣2；‎ ‎（2）如图1，∵△PQD是等边三角形，‎ ‎∴∠PDQ=60°，‎ ‎∴∠PDB+∠CDQ=120°，‎ ‎∵△ABC是等边三角形，‎ ‎∴∠B=∠C=60°，‎ ‎∴∠PDB+∠BPD=120°，‎ ‎∴∠BPD=∠CDQ，‎ ‎∵BD=CD，‎ 在△BPD与△CDQ中，‎ ‎，‎ ‎∴△BPD≌△CDQ（AAS），‎ ‎∴BP=CQ，‎ ‎∴2﹣t=t，‎ ‎∴t=1，‎ ‎（3）当0≤t≤2时，如图2，连接AD，‎ ‎∵△ABC是等边三角形，D是边BC的中点，‎ ‎∴∠ADB=90°，‎ ‎∴AD=AB•sin60°=，‎ 分别过点P，Q作PE⊥BC，QF⊥BC，垂足分别为点E，F，‎ 在Rt△BPE中，∠BEP=90°，PE=PB•sin60°=，‎ 在Rt△QCF中，∠QFC=90°，QF=CQ•sin60°=，‎ 过点Q作QG⊥AB于点G，‎ 在Rt△AGQ中，∠AGQ=90°，QG=AQ•sin60°=，‎ ‎∴S△PQD=S△ABC﹣S△BPD﹣S△QCD﹣S△APQ，‎ ‎∴‎ ‎∴，‎ 当2＜t＜3时，如图3‎ 过点Q作QH⊥BC于点H，‎ 在Rt△CQH中，∠CHQ=90°，‎ QH=CQ•sin60°=，‎ ‎∴‎ ‎∴．‎ ‎（4）点D′落在△ABC的边上，如图4，此时t=1；‎ 点D′落在△ABC的边上，如图5，此时t=2.5．‎ ‎17．在Rt△AOB中，OA=3，sinB=，P、M、分别是BA、BO边上的两个动点．点M从点B出发，沿BO以1单位/秒的速度向点O运动；点P从点B出发，沿BA以a单位/秒的速度向点A运动；P、M两点同时出发，任意一点先到达终点时，两点停止运动．设运动的时间为t．‎ ‎（1）线段AP的长度为　5﹣at　（用含a、t的代数式表示）；‎ ‎（2）如图①，连结PO、PM，若a=1，△PMO的面积为S，试求S的最大值；‎ ‎（3）如图②，连结PM、AM，试探究：在点P、M运动的过程中，是否存在某个时刻，使得△PMB为直角三角形且△PMA是等腰三角形？若存在，求出此时a和t的取值，若不存在，请说明理由．‎ 解：（1）∵Rt△AOB中，OA=3，sinB=，‎ ‎∴AB=5，‎ ‎∵设运动的时间为t，点P从点B出发，沿BA以a单位/秒的速度向点A运动，‎ ‎∴AP=5﹣at，‎ 故答案为：5﹣at；‎ ‎（2）如图①：‎ 过点P作PD⊥OB，在Rt△PDB中，PB=t，sinB=，‎ ‎∴PD=，OM=4﹣t，‎ ‎∴，‎ ‎∵0≤t≤4，‎ ‎∴当t=2时，；‎ ‎（3）假设存在，‎ ‎①若∠PMB=90°，如图②：‎ ‎∵PA=PM，‎ 在Rt△PMB中，PB=at，sinB=，‎ ‎∴PM=at，MB=at，‎ 根据题意可得：，‎ 解得：，符合题意；‎ ‎②若∠MPB=90°，如图③，则∠APM=90°，‎ ‎∴PA=PM，‎ 在Rt△PMB中，PB=at，sinB=，‎ ‎∴，‎ 根据题意可得：，‎ 解得：，符合题意，‎ ‎∴存在某时刻，使得△PMB为直角三角形且△PMA是等腰三角形，此时．‎ ‎18．在直角△ABC中，∠ACB=90°，点E在AC边上，连结BE，作∠ACF=∠CBE交AB于点F，同时点D在BE上，且CD⊥AB．‎ ‎（1）已知：如图，，．‎ ‎①求证：△ACF≌△BCD．‎ ‎②求的值．‎ ‎（2）若，，则的值是多少（直接写出结果）‎ 证明：（1）①∵∠ACB=90°，，CG⊥AB，‎ 由等腰三角形的三线合一的性质可得：CD是∠ACB的角平分线，∠BCD=45°，‎ 在△CAF与△BCD中，‎ ‎，‎ ‎∴△ACF≌△BCD；‎ ‎②由①可知：∠AFC=∠CDB，‎ ‎∴∠CFB=∠CDE，‎ ‎∵∠CBF=∠ECD=45°，‎ ‎∴△CDE∽△BFC，‎ ‎∴；‎ ‎（2）∵，‎ ‎∵，，‎ ‎∴．‎ ‎19．已知，AB=5，tan∠ABM=，点C、D、E为动点，其中点C、D在射线BM上（点C在点D的左侧），点E和点D分别在射线BA的两侧，且AC=AD，AB=AE，∠CAD=∠BAE．‎ ‎（1）当点C与点B重合时（如图1），联结ED，求ED的长；‎ ‎（2）当EA∥BM时（如图2），求四边形AEBD的面积；‎ ‎（3）联结CE，当△ACE是等腰三角形时，求点B、C间的距离．‎ 解：（1）如图1中，延长BA交DE于F，作AH⊥BD于H．‎ 在RT△ABH中，∵∠AHB=90°，‎ ‎∴sin∠ABH==，‎ ‎∴AH=3，BH==4，‎ ‎∵AB=AD，AH⊥BD，‎ ‎∴BH=DH=4，‎ 在△ABE 和△ABD中，‎ ‎，‎ ‎∴△ABD≌△ABE，‎ ‎∴BE=BD，∠ABE=∠ABD，‎ ‎∴BF⊥DE，EF=DF，‎ ‎∵∠ABH=∠DBF，∠AHB=∠BFD，‎ ‎∴△ABH∽△DBF，‎ ‎∴=，‎ ‎∴DF=，‎ ‎∴DE=2DF=．‎ ‎（2）如图2中，作AH⊥BD于H．‎ ‎∵AC=AD，AB=AE，∠CAD=∠BAE，‎ ‎∴∠AEB=∠ABE=∠ACD=∠ADC，‎ ‎∵AE∥BD，‎ ‎∴∠AEB+∠EBD=180°，‎ ‎∴∠EBD+∠ADC=180°，‎ ‎∴EB∥AD，‎ ‎∵AE∥BD，‎ ‎∴四边形ADBE是平行四边形，‎ ‎∴BD=AE=AB=5，AH=3，‎ ‎∴S平行四边形ADBE=BD•AH=15．‎ ‎（3）由题意AC≠AE，EC≠AC，只有EA=EC．‎ 如图3中，‎ ‎∵∠ACD=∠AEB（已证），‎ ‎∴A、C、B、E四点共圆，‎ ‎∵AE=EC=AB，‎ ‎∴=，‎ ‎∴=，‎ ‎∴∠AEC=∠ABC，‎ ‎∴AE∥BD，‎ 由（2）可知四边形ADBE是平行四边形，‎ ‎∴AE=BD=AB=5，‎ ‎∵AH=3，BH=4，‎ ‎∴DH=BD﹣BH=1，‎ ‎∵AC=AD，AH⊥CD，‎ ‎∴CH=HD=1，‎ ‎∴BC=BD﹣CD=3．‎ ‎20．在△ABC中，D、E、F分别为BC、AB、AC上的点．‎ ‎（1）如图1，若EF∥BC、DF∥AB，连CE、AD分别交DF、EF于N、M，且E为AB的中点，求证：EM=MF；‎ ‎（2）如图2，在（1）中，若E不是AB的中点，请写出与MN平行的直线，并证明；‎ ‎（3）若BD=DC，∠B=90°，且AE：AB：BC=1：3：2，AD与CE相交于点Q，直接写出tan∠CQD的值．‎ ‎（1）证明：如图1中，‎ ‎∵AE=EB，EF∥AC，‎ ‎∴AF=FC，AM=MD，∵FD∥AB，‎ ‎∴BD=CD，‎ ‎∴EM=BD，MF=CD，‎ ‎∴EM=MF．‎ ‎（2）结论：MN∥AC．‎ 证明：如图2中，‎ ‎∵AE∥DF，‎ ‎∴=，‎ ‎∵MF∥BC，‎ ‎∴=，‎ ‎∵FN∥AE，‎ ‎∴=，‎ ‎∴=，‎ ‎∴MN∥CF．‎ ‎（3）如图3中，作DN∥AB交CE于N，CM⊥AD交AD的延长线于M．‎ ‎∵AE：AB：BC=1：3：2，‎ 不妨设AE=a．则AB=3a，EB=2a．BC=2a，BD=DC=a，‎ ‎∴tan∠BAD═=，‎ ‎∴∠BAD=30°，∠ADB=∠CDM=60°，‎ ‎∴∠DCM=30°，‎ ‎∴DM=a，CM=a，'‎ ‎∵BD=DC，DN∥EB，‎ ‎∴EN=NC，‎ ‎∴DN=EB=a=AE，‎ ‎∵AE∥DN，‎ ‎∴∠EAQ=∠NDQ，‎ 在△AEQ和△DNQ中，‎ ‎，‎ ‎∴△AEQ≌△DNQ，‎ ‎∴AQ=QD，‎ ‎∵AD===2a，‎ ‎∴DQ=a，QM=DQ+DM=a，‎ ‎∴tan∠CQD===．‎ ‎21．我们把两条中线互相垂直的三角形称为“中垂三角形”．例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P．像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．‎ 特例探索 ‎（1）①如图1，当∠ABE=45°，时，a=　2　，b=　2　；‎ ‎②如图2，当∠ABE=30°，c=4时，求a和b的值 归纳证明 ‎（2）请你观察（1）中的计算结果，猜想三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．‎ 解：（1）①当∠ABE=45°，时，a=，b=‎ 如图1，‎ 连接EF，则EF是△ABC的中位线 ‎∴EF==，‎ ‎∵∠ABE=45°，AE⊥EF ‎∴△ABP是等腰直角三角形，‎ ‎∵EF∥AB，‎ ‎∴△EFP也是等腰直角三角形，‎ ‎∴AP=BP=2，EP=FP=1，‎ ‎∴AE=BF=，‎ ‎∴.‎ ‎②如图2，‎ 连接EF，则EF是△ABC的中位线．‎ ‎∵∠ABE=30°，AE⊥BF，AB=4，‎ ‎∴AP=2，BP=，‎ ‎∵EF∥AB，EF=AB，PE=，PF=1‎ ‎∴AE=，BF=‎ ‎∴，． ‎ ‎（2）a2+b2=5c2‎ 如图3，‎ 连接EF，设AP=m，BP=n，‎ 则c2=AB2=m2+n2，‎ ‎∵EF∥AB，EF=AB，‎ ‎∴PE=BP=n，PF=AP=m，‎ ‎∴，，‎ ‎∴b2=AC2=4AE2=4m2+n2，a2=BC2=4BF2=4n2+m2‎ ‎∴a2+b2=5（m2+n2）=5c2．‎ ‎22．如图，一个直角三角形纸片的锐角顶点A在∠MCN的边OM上移动，移动过程中始终有AB⊥ON于点B，AC⊥OM于点A，∠MON的平分线OP分别交AB，AC于点D、E．‎ ‎（1）点A在移动的过程中，线段AD和AE有怎样的数量关系？（不必证明）‎ ‎（2）点A在移动的过程中，若射线ON上始终存在一点F与点A关于OP所在的直线对称，判断并证明以A、D、F、E为顶点的四边形是什么特殊四边形？‎ ‎（3）若∠MON=45°，猜想线段AC、AD、OC之间有怎样的数量关系？请证明你的猜想．‎ 解：（1）结论：AD=AE．‎ 理由：如图1中，‎ ‎∵AB⊥OC，CA⊥OA，‎ ‎∴∠ABO=∠OAE=90°，‎ ‎∴∠AEO=90°﹣∠AOE，'∠ADE=∠ODB=90°﹣∠BOD，‎ ‎∵∠AOE=∠BOD，‎ ‎∴∠ADE=∠AED，‎ ‎∴AD=AE．‎ ‎（2）结论：四边形ADFE是菱形．‎ 理由：如图2中，连接DF、EF．‎ ‎∵点A、F关于直线OP对称，E、D在OP上，‎ ‎∴AE=FE，AD=FD，‎ ‎∵AD=AE，‎ ‎∴AE=EF=AD=FD，‎ ‎∴四边形ADFE是菱形．‎ ‎（3）结论：OC=AC+AD．‎ 理由：如图2中，‎ ‎∵点F与点A关于直线OP对称，‎ ‎∴AO=OF，‎ ‎∵AC⊥OH，∠MON=45°，‎ ‎∴∠OAC=90°，‎ ‎∴∠ACO=∠MON=45°，‎ ‎∴OF=AO=AC，‎ 由（2）可知四边形ADFE是菱形，‎ ‎∴EF∥AB，AD=EF，‎ ‎∵AB⊥ON，‎ ‎∴∠ABC=90°，‎ ‎∴∠EFC=∠ABC=90°，‎ ‎∵∠ACO=45°，‎ ‎∴∠ACO=∠CEF，‎ ‎∴CF=EF=AD，‎ ‎∵OC=OF+FC，‎ ‎∴OC=AC+AD．‎ ‎23．如图①，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与点A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM，射线AE于点F、D．‎ ‎（1）问题发现：直接写出∠NDE=　90　度；‎ ‎（2）拓展探究：试判断，如图②当∠EAC为钝角时，其他条件不变，∠NDE的大小有无变化？请给出证明．‎ ‎（3）如图③，若∠EAC=15°，BD=，直线CM与AB交于点G，其他条件不变，请直接写出AC的长．‎ 解：（1）∵∠ACB=90°，∠MCN=90°，‎ ‎∴∠ACM=∠BCN，‎ 在△MAC和△NBC中，‎ ‎，‎ ‎∴△MAC≌△NBC，‎ ‎∴∠NBC=∠MAC=90°，‎ 又∵∠ACB=90°，∠EAC=90°，‎ ‎∴∠NDE=90°．‎ 故答案为：90．‎ ‎（2）∠NDE的大小不变，‎ 在△MAC和△NBC中，‎ ‎，‎ ‎∴△MAC≌△NBC，‎ ‎∴∠N=∠AMC，‎ 又∵∠MFD=∠NFC，‎ ‎∴∠MDF=∠FCN=90°，‎ 即∠NDE=90°．‎ ‎（3）AC=2，‎ 在△MAC和△NBC中，‎ ‎，‎ ‎∴△MAC≌△NBC，‎ ‎∴∠NBC=∠MAC=15°，‎ 如图③，设BC与AD交于点H，‎ 又∵∠AHC=∠BHD，‎ ‎∴∠BDH=∠ACH=90°，‎ ‎∴在Rt△ABD中，∠ABD=∠ABC+∠NBC=45°+15°=60°‎ ‎∵BD=，‎ ‎∴AB=2，‎ ‎∴AC=AB•cos45°=2．‎ ‎24．在△ABC中，∠ABC=2∠ACB，延长AB至点D，使BD=BC，点E是直线BC上一点，点F是直线AC上一点，连接DE．连接EF，且∠DEF=∠DBC．‎ ‎（1）如图1，若∠D=∠EFC=15°，AB=，求AC的长．‎ ‎（2）如图2，当∠BAC=45°，点E为线段BC的延长线上，点F在线段AC的延长线上时，求证：CF=BE．‎ ‎（3）如图3，当∠BAC=90°，点E为线段CB的延长线上，点F在线段CA的延长线上时，猜想线段CF与线段BE的数量关系，并证明猜想的结论．‎ ‎（1）解：在△BDE中，∠D+∠DBE+∠BED=180°，‎ ‎∵∠DEB+∠DEF+∠FEC=180°，∠DEF=∠DBC，‎ ‎∴∠D=∠FEC=∠F=15°，‎ ‎∴∠ACB=∠F+∠CEF=30°，‎ 在Rt△ABC中，∵∠BAC=90°，AB=，∠ACB=30°，‎ ‎∴BC=2AB=2，‎ ‎∴AC===3．‎ ‎（2）证明：如图2中，连接CD，作EM⊥EB交AF于M，作FN⊥BE于N，AF交DE于点O．‎ ‎∵∠BAC=45°，∠ABC=2∠ACB，‎ ‎∴∠ABC=90°，∠ACB=∠MCE=∠EMC=45°，‎ ‎∴EM=EC，‎ ‎∵BD=DC，‎ ‎∴∠BDC=∠BCD=45°，‎ ‎∴∠DCE=∠EMF=135°，‎ ‎∵∠DEF=∠DBC=90°，∠FCD=∠DCA=90°，‎ ‎∴∠OEF=∠OCD，∵∠EOF=∠COD，‎ ‎∴∠OFE=∠ODC，‎ 在△EMF和△ECD中，‎ ‎，‎ ‎∴△EMC≌△ECD，‎ ‎∴EF=DE，‎ ‎∵∠DEB+∠FEN=90°，∠EFN+∠FEN=90°，‎ ‎∴∠EFN=∠DEB，‎ 在△EFN和△DEB中，‎ ‎，‎ ‎∴△EFN≌△DEB，‎ ‎∴DB=EN=BC，‎ ‎∴BE=CN，‎ ‎∵△CFN是等腰直角三角形，‎ ‎∴CF=CN=BE．‎ ‎（3）结论：CF=BE．‎ 理由：如图3中，连接CD、DF、作NE⊥CE交AD的延长线于N，在线段CE上截取一点M，使得FM=FE．‎ ‎∵∠BAC=90°，∠ABC=2∠ACB，‎ ‎∴∠ABC=60°，∠ACB=30°，‎ ‎∵DB=BC，‎ ‎∴∠DBC=120°，∠BDC=∠BCD=30°，‎ ‎∴∠DBC=∠DEF=120°，∠DCA=∠DCB+∠ACB=60°，‎ ‎∴∠DEF+∠DCF=180°，‎ ‎∴E、F、C、D四点共圆，‎ ‎∵∠DCE=∠ECF，‎ ‎∴=，‎ ‎∴DE=EF=FM，‎ ‎∵∠NEB=90°，∠NBE=∠ABC=60°，‎ ‎∴∠N=∠ACM=30°，‎ ‎∵∠DBC=∠BDE+∠DEB=∠DEB+∠FEM=∠DEB+∠FME，‎ ‎∴∠BDE=∠FME，‎ ‎∴∠NDE=∠FMC，‎ 在△EDN和△FMC中，‎ ‎，‎ ‎∴△EDN≌△CMF，‎ ‎∴NE=CF，‎ 在Rt△NEB中，∵∠NEB=90°，∠N=30°，‎ ‎∴NE=BE，‎ ‎∴CF=BE．‎ ‎25．中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形！‎ ‎（1）如图1，若点D为等腰直角三角形ABC斜边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°，连接AD、EF，当BC=5，FC=2时，求EF的长度；‎ ‎（2）如图2，若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°；M为EF的中点，连接CM，当DF∥AB时，证明：3ED=2MC；‎ ‎（3）如图3，若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°；当BE=6，CF=0.8时，直接写出EF的长度．‎ 解：（1）如图1∵点D为等腰直角三角形ABC斜边BC的中点 ‎∴AD⊥BC，AD=BC=CD=，∠DAE=∠C=45°‎ ‎∴AC=CD=5‎ 又∵∠EDF=90°，FC=2‎ ‎∴∠ADE=∠CDF，AF=5﹣2=3‎ 在△ADE和△CDF中 ‎∴△ADE≌△CDF（ASA）‎ ‎∴AE=CF=2‎ ‎∴在Rt△AEF中，EF==‎ ‎（2）设等边三角形边长为2，则BD=CD=1‎ ‎∵等边三角形ABC中，DF∥AB ‎∴∠FDC=∠B=60°‎ ‎∵∠EDF=90°‎ ‎∴∠BDE=30°‎ ‎∴DE⊥BE ‎∴BE=，DE=‎ 如图2，连接DM，则Rt△DEF中，DM=EF=FM ‎∵∠FDC=∠FCD=60°‎ ‎∴△CDF是等边三角形 ‎∴CD=CF=1‎ ‎∴CM垂直平分DF ‎∴∠DCN=30°‎ ‎∴Rt△CDN中，DN=，CN=，DF=1‎ ‎∴在Rt△DEF中，EF==‎ ‎∵M为EF的中点 ‎∴FM=DM=‎ ‎∴Rt△MND中，MN==‎ ‎∴CM=+=‎ ‎∴==‎ ‎∴3ED=2MC ‎（3）如图3，延长FD至G，使得FD=DG，连接EG，BG，则ED垂直平分FG，故EF=EG ‎∴由BD=CD，∠BDG=∠CDF，DF=DG可得：△BDG≌△CDF ‎∴∠GBD=∠C=60°，BG=CF=0.8‎ ‎∴∠EBG=60°+60°=120°‎ ‎∴∠EBH=60°‎ 过E作EH⊥BG于点H，则BH=BE=3‎ ‎∴Rt△BEH中，HE==3‎ ‎∴Rt△EHG中，EG==‎ ‎∴EF的长度为 ‎26．已知，△ABC为直角三角形，∠ACB=90°，点P是射线CB上一点（点P不与点B、C重合），线段AP绕点A顺时针旋转90°得到线段AQ，连接QB交射线AC于点M．‎ ‎（1）如图①，当AC=BC，点P在线段CB上时，线段PB、CM的数量关系是　PB=2CM　；‎ ‎（2）如图②，当AC=BC，点P在线段CB的延长线时，（1）中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由．‎ ‎（3）如图③，若，点P在线段CB的延长线上，CM=2，AP=13，求△ABP的面积．‎ 解：（1）如图1，‎ 将△ABC绕点A顺时针旋转90°，得到△AB'C'，‎ ‎∴B'Q=BP，AB'=AB，‎ 连接BB'，‎ ‎∵AC⊥BC，‎ ‎∴点C在BB'上，且CB'=CB，‎ 依题意得，∠C'B'B=90°，‎ ‎∴CM∥B'C'，而CB'=CB，‎ ‎∴2CM=B'Q，‎ ‎∵BP=B'Q，‎ ‎∴BP=2CM，‎ 故答案为：BP=2CM；‎ ‎（2）BP=2CM仍然成立，‎ 理由：如图2，‎ 将△ABC绕点A顺时针旋转90°，得到△AB'C'，连接B'Q，‎ ‎∴B'Q=BP，AB'=AB，‎ 连接BB'，‎ ‎∵AC⊥BC，‎ ‎∴点C在BB'上，且CB'=CB，‎ 依题意得，∠C'B'B=90°，‎ ‎∴CM∥B'C'，而CB'=CB，‎ ‎∴2CM=B'Q，‎ ‎∵BP=B'Q，‎ ‎∴BP=2CM，‎ ‎（3）如图3，‎ 设BC=2x，则AC=5x，‎ 将△ABC绕点A顺时针旋转90°，得到△AB'C'，连接B'Q，‎ ‎∴BC=B'C'，B'Q=BP，AC=AC'‎ 延长BC交C'Q于N，‎ ‎∴四边形ACNC'是正方形，‎ ‎∴C'N=CN=AC=5x，‎ ‎∴BN=CN+BC=7x ‎∵CM∥QN，‎ ‎∴‎ ‎∵CM=2，‎ ‎∴‎ ‎∴QN=7，‎ ‎∴BP=B'Q=C'N+QN﹣B'C'=5x+7﹣2x=3x+7，‎ ‎∴PC=BC+BP=2x+3x+7=5x+7，‎ 在Rt△ACP中，AC=5x，PC=5x+7，AP=13，‎ 根据勾股定理得，（5x）2+（5x+7）2=132‎ ‎∴x=1或x=﹣（舍），‎ ‎∴BP=3x+7=10，AC=5x=5，‎ ‎∴S△ABP=BP×AC=×10×5=25，‎ ‎27．在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．‎ ‎（1）如图1，若点F与点A重合，求证：AC=BC；‎ ‎（2）若∠DAF=∠DBA，‎ ‎①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；‎ ‎②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．‎ 解：（1）由旋转得，∠BAC=∠BAD，‎ ‎∵DF⊥AC，‎ ‎∴∠CAD=90°，‎ ‎∴∠BAC=∠BAD=45°，‎ ‎∵∠ACB=90°，‎ ‎∴∠ABC=45°，‎ ‎∴AC=CB，‎ ‎（2）①由旋转得，AD=AB，‎ ‎∴∠ABD=∠ADB，‎ ‎∵∠DAF=∠ABD，‎ ‎∴∠DAF=∠ADB，‎ ‎∴AF∥BD，‎ ‎∴∠BAC=∠ABD，‎ ‎∵∠ABD=∠FAD 由旋转得，∠BAC=∠BAD，‎ ‎∴∠FAD=∠BAC=∠BAD=×180°=60°，‎ 由旋转得，AB=AD，‎ ‎∴△ABD是等边三角形，‎ ‎∴AD=BD，‎ 在△AFD和△BED中，‎ ‎，‎ ‎∴△AFD≌△BED，‎ ‎∴AF=BE，‎ ‎②如图，‎ 由旋转得，∠BAC=∠BAD，‎ ‎∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD，‎ 由旋转得，AD=AB，‎ ‎∴∠ABD=∠ADB=2∠BAD，‎ ‎∵∠BAD+∠ABD+∠ADB=180°，‎ ‎∴∠BAD+2∠BAD+2∠BAD=180°，‎ ‎∴∠BAD=36°，‎ 设BD=y，作BG平分∠ABD，‎ ‎∴∠BAD=∠GBD=36°‎ ‎∴AG=BG=BD=y，‎ ‎∴DG=AD﹣AG=AD﹣BG=AD﹣BD，‎ ‎∵∠BDG=∠ADB，‎ ‎∴△BDG∽△ADB，‎ ‎∴．‎ ‎∴=﹣1，即（）2﹣﹣1=0，‎ ‎∴，‎ ‎∵∠FAD=∠EBD，∠AFD=∠BED，‎ ‎∴△AFD∽△BED，‎ ‎∴，‎ ‎∴AF==x．‎ ‎28．如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．‎ ‎（1）求证：DE⊥AG；‎ ‎（2）正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°）得到正方形OE′F′G′，如图2．‎ ‎①在旋转过程中，当∠OAG′是直角时，求α的度数；‎ ‎②若正方形ABCD的边长为1，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．‎ 解：（1）如图1，延长ED交AG于点H，‎ ‎∵点O是正方形ABCD两对角线的交点，‎ ‎∴OA=OD，OA⊥OD，‎ ‎∵OG=OE，‎ 在△AOG和△DOE中，‎ ‎，‎ ‎∴△AOG≌△DOE，‎ ‎∴∠AGO=∠DEO，‎ ‎∵∠AGO+∠GAO=90°，‎ ‎∴∠GAO+∠DEO=90°，‎ ‎∴∠AHE=90°，‎ 即DE⊥AG；‎ ‎（2）‎ ‎①在旋转过程中，∠OAG′成为直角有两种情况：‎ ‎（Ⅰ）α由0°增大到90°过程中，当∠OAG′=90°时，‎ ‎∵OA=OD=OG=OG′，‎ ‎∴在Rt△OAG′中，sin∠AG′O==，‎ ‎∴∠AG′O=30°，‎ ‎∵OA⊥OD，OA⊥AG′，‎ ‎∴OD∥AG′，‎ ‎∴∠DOG′=∠AG′O=30°，‎ 即α=30°；‎ ‎（Ⅱ）α由90°增大到180°过程中，当∠OAG′=90°时，‎ 同理可求∠BOG′=30°，‎ ‎∴α=180°﹣30°=150°．‎ 综上所述，当∠OAG′=90°时，α=30°或150°．‎ ‎②如图3，当旋转到A、O、F′在一条直线上时，AF′的长最大，‎ ‎∵正方形ABCD的边长为1，‎ ‎∴OA=OD=OC=OB=，‎ ‎∵OG=2OD，‎ ‎∴OG′=OG=，‎ ‎∴OF′=2，‎ ‎∴AF′=AO+OF′=+2，‎ ‎∵∠COE′=45°，‎ ‎∴此时α=315°．‎ ‎29．在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E．DF与线段AC（或AC的延长线）相交于点F．‎ ‎（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；‎ ‎（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=AB；‎ ‎（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线相交于点F，作DN⊥AC于点N，若DN⊥AC于点N，若DN=FN，求证：BE+CF=（BE﹣CF）．‎ 解：（1）如图1，‎ ‎∵AB=AC，∠A=60°，‎ ‎∴△ABC是等边三角形，‎ ‎∴∠B=∠C=60°，BC=AC=AB=4．‎ ‎∵点D是线段BC的中点，‎ ‎∴BD=DC=BC=2．‎ ‎∵DF⊥AC，即∠AFD=90°，‎ ‎∴∠AED=360°﹣60°﹣90°﹣120°=90°，‎ ‎∴∠BED=90°，‎ ‎∴BE=BD×cos∠B=2×cos60°=2×=1；‎ ‎（2）过点D作DM⊥AB于M，作DN⊥AC于N，如图2，‎ 则有∠AMD=∠BMD=∠AND=∠CND=90°．‎ ‎∵∠A=60°，∴∠MDN=360°﹣60°﹣90°﹣90°=120°．‎ ‎∵∠EDF=120°，∴∠MDE=∠NDF．‎ 在△MBD和△NCD中，‎ ‎，‎ ‎∴△MBD≌△NCD，‎ ‎∴BM=CN，DM=DN．‎ 在△EMD和△FND中，‎ ‎，‎ ‎∴△EMD≌△FND，‎ ‎∴EM=FN，‎ ‎∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN ‎=2BM=2BD×cos60°=BD=BC=AB；‎ ‎（3）过点D作DM⊥AB于M，如图3．‎ 同（1）可得：∠B=∠ACD=60°．‎ 同（2）可得：BM=CN，DM=DN，EM=FN．‎ ‎∵DN=FN，∴DM=DN=FN=EM，‎ ‎∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM，‎ BE﹣CF=BM+EM﹣CF=BM+NF﹣CF=BM+NC=2BM．‎ 在Rt△BMD中，DM=BM•tanB=BM，‎ ‎∴BE+CF=（BE﹣CF）．‎ ‎30．如图1所示，在菱形ABCD和菱形AEFG中，点A，B，E在同一条直线上，P是线段CF的中点，连接PD，PG．‎ ‎（1）若∠BAD=∠AEF=120°，请直接写出∠DPG的度数及的值．‎ ‎（2）若∠BAD=∠AEF=120°，将菱形ABCD绕点A顺时针旋转，使菱形ABCD的对角线AC恰好与菱形AEFG的边AE在同一直线上，如图2，此时，（1）中的两个结论是否发生改变？写出你的猜想并加以说明．‎ ‎（3）若∠BAD=∠AEF=180°﹣2α（0°＜α＜90°），将菱形ABCD绕点A顺时针旋转到图3的位置，求出的值．‎ 解：（1）延长GP交CD于H，如图1所示：‎ ‎∵在菱形ABCD和菱形AEFG中，‎ AB=CD=AD，BE∥CD，AG=FG，FG∥BE，‎ ‎∴FG∥CD，‎ ‎∴∠PFG=∠PCH，‎ ‎∵P是线段CF的中点，‎ ‎∴PF=PC，‎ 在△PFG和△PCH中，‎ ‎，‎ ‎∴△PFG≌△PCH（ASA），‎ ‎∴FG=CH，PG=PH，‎ ‎∴AG=CH，‎ ‎∴DG=DH，‎ ‎∴DP⊥GH（三线合一），‎ ‎∴∠DPG=90°；‎ ‎∵∠BAD=120°，‎ ‎∴∠ADC=60°，‎ ‎∴∠PDG=∠PDH=∠ADC=30°，‎ ‎∴=tan∠PDG=tan30°=；‎ ‎（2）（1）中的两个结论不发生改变；理由如下：‎ 延长GP交CE于H，连接DH、DG，如图2所示：‎ ‎∵四边形AEFG为菱形，‎ ‎∴FG∥EC，‎ ‎∴∠GFP=∠HCP，‎ ‎∵P是线段CF的中点，‎ ‎∴PF=PC，‎ 在△PFG和△PCH中，‎ ‎，‎ ‎∴△PFG≌△PCH（ASA），‎ ‎∴FG=CH，PG=PH，‎ ‎∵FG=AG，‎ ‎∴AG=CH，‎ ‎∵四边形ABCD是菱形，‎ ‎∴AC=CD，‎ ‎∵∠BAD=∠AEF=120°，‎ ‎∴∠ACD=60°，‎ ‎∴△ACD是等边三角形，‎ ‎∴AD=CD，‎ ‎∴∠EAG=∠ADC=60°，∠DAC=∠DCA=60°，‎ ‎∴∠GAD=180°﹣∠EAG﹣∠DAC=60°，‎ 在△ADG和△CDH中，‎ ‎，‎ ‎∴△ADG≌△CDH（SAS），‎ ‎∴DG=DH，∠ADG=∠CDH，‎ ‎∴DP⊥GH，‎ ‎∴∠DPG=90°，∠GDH=∠ADC=60°，‎ ‎∴∠GDP=30°，‎ ‎∴=tan30°=；‎ ‎（3）延长GP到H，使得PH=GP，连接CH、DG、DH，延长DC交EA的延长线于点M，如图3所示：‎ 同（2）可证△PFG≌△PCH，‎ ‎∴∠GFC=∠HCF，FG=CH，‎ ‎∴FG∥CH，‎ ‎∵FG∥AE，‎ ‎∴CH∥EM，‎ ‎∴∠DCH=∠M，‎ ‎∵CD∥AB，‎ ‎∴∠M=∠MAB，‎ ‎∴∠DCH=∠MAB，‎ ‎∵∠BAD=∠AEF=180°﹣2α，‎ ‎∴∠EAG=∠ADC=2α，‎ ‎∴∠GAM=180°﹣2α，‎ ‎∴∠GAD=∠BAM，‎ ‎∴∠GAD=∠DCH，‎ ‎∵AG=FG，‎ ‎∴AG=CH，‎ 在△ADG和△CDH中，‎ ‎，‎ ‎∴△ADG≌△CDH（SAS），‎ ‎∴∠ADG=∠CDH，DG=DH，‎ ‎∴∠GDH=∠ADC=2α，‎ ‎∴∠DPG=90°，∠GDP=∠GDH=α，‎ ‎∴=tanα．‎