- 2022-08-29 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中各类方程的解法及练习
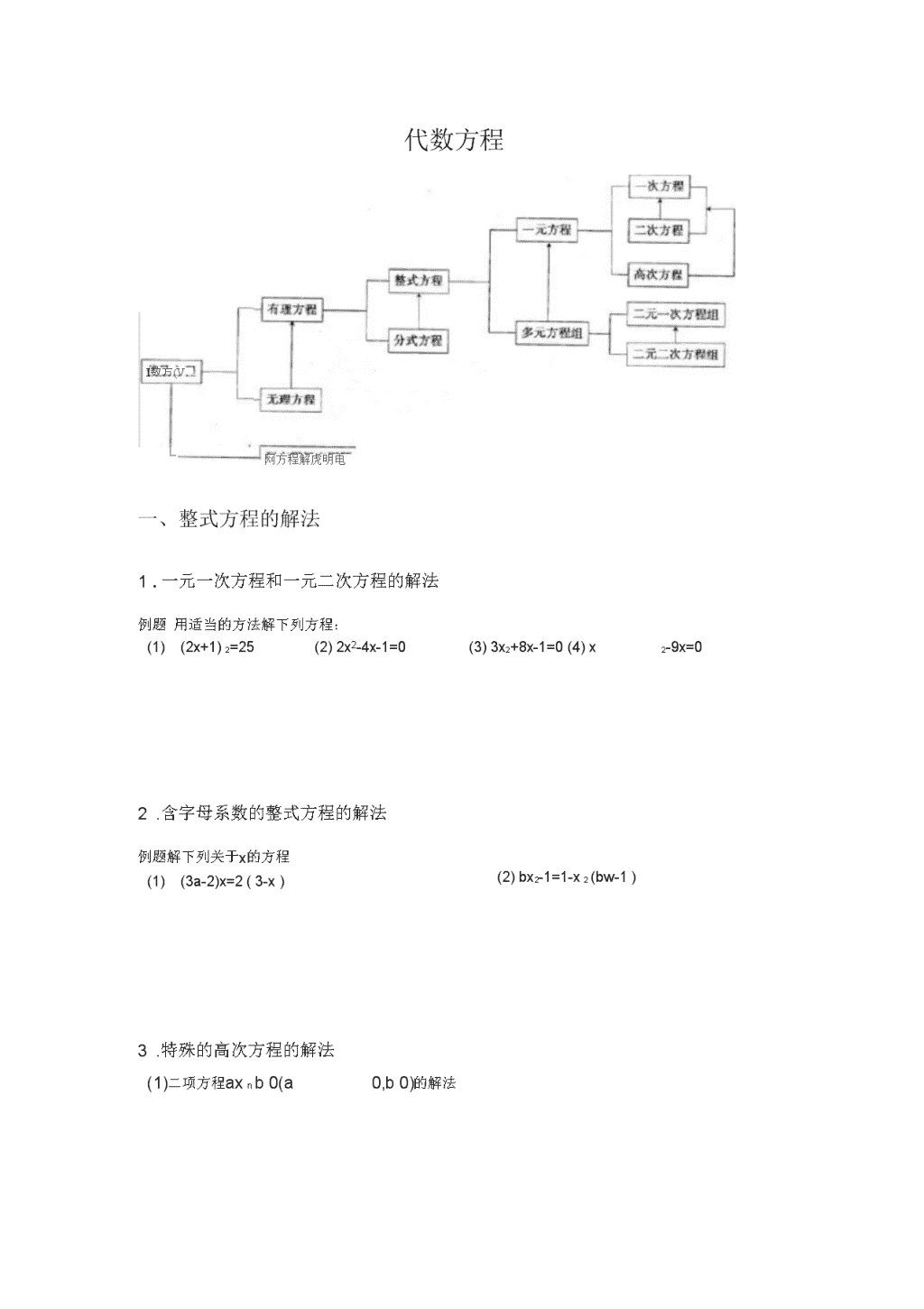
代数方程I数方(VL网方程解虎明电一、整式方程的解法1.一元一次方程和一元二次方程的解法例题用适当的方法解下列方程:(1)(2x+1)2=25(2)2x2-4x-1=0(3)3x2+8x-1=0(4)x2-9x=02.含字母系数的整式方程的解法(2)bx2-1=1-x2(bw-1)例题解下列关于x的方程(1)(3a-2)x=2(3-x)3.特殊的高次方程的解法(1)二项方程axnb0(a0,b0)的解法\n例题判断下列方程是不是二项方程,如果是二项方程,求出它的根。(1)x3-64=0(2)x4+x=0(3)x5=-9(4)x3+x=1(2)双二次方程ax4bx2c0(a0)的解法例题判断下列方程是不是双二次方程,如果是,求出它的根:(1)x4-9x2+14=0⑵x4+10x+25=0(3)2x4-7x3-4=0(4)x4+9x2+20=0(3)因式分解法解高次方程(2)x3-2x2+x-2=0例题解下列方程:(1)2x3+7x2-4x=04.二元二次方程组例题解下列方程组⑴4x29y215⑵x23xy2y202x3y5x2y25二、可化为一元二次方程的分式方程的解法例题解下列方程一、4x3x45(1)-2x512xx1760\n2XX__⑵—5—60x1x1(3)一2一8(x2x)x21-23(x1)x22x11三、无理方程的解法1.只有一个含未知数根式的无理方程例题解下列方程:11)2jx3x6(2)3J2x3x2.有两个含未知数根式的无理方程例题解下列方程:(2)x2(1)Jx22J2x103.适宜用换元法解的无理方程例题解方程2&—2^―43x26x4\n代数方程练习则原方程化为关于y的方程1.在方程3x25Vx210中,若设“21V,2.当m=时,关于x的分式方程x2x0没有实数解.3.若关于x的方程J2""x&a0有实数根,则的取值范围是6x0=y,这时原方程变5.方程xx0的根是x的根是x的根6.无理方程Yx26ax的根为03,则a的值为7.若a,b都是正实数,且ab2b28.若a+b=1,且a:b=2:5,贝U2a-b=9.当a=.时,方程0无实数根.3.用换元法解方程x00x1.8x110.若x,则x11.下列方程中既不是分式方程,也不是无理方程的有(A.12xB.2x2、3C.3x3x5xD.3E.2x43y,53xF.112.方程2(x3)23(x3)(x3)x4(x3)的最简公分母是A.24(x+3)C.24(x+3)(x-3)(x-3)B.(x+3)(x-3)D.12(x+3)(x-3)20x(x3)0x2D.13.观察下列方程,经分析判断得知有实数根的是32——0——30A.x3B.x1C.0\n14.如果A.115.方程16.A.016.设yA.y216xB.-12xC.B.2A.全体实数18.已知C.0那么x的值是(的解是1,则方程0B.4a2B.aVRSD.4D.2a,则a>0VA.RSSUB.1;xx可变形为20C.的取值范围是C.aD.D.AS0),则相等关系成立的式子是(SURSSURD.23.23.x221.xx3x3x22.22A.x=aB.x=-aC.x1=a;x2=-aD.x产a;x2=a20.一个数和它的算术平方根的4倍相等,那么这个数是()A.0B.16C.0或16D.4或16x的根是(19.关于)x的方程23.23.\n2x16x124.x1331x2xx123.查看更多