2013-2014下学期宝安中学高一理科数学(含答案)

2013-2014下学期宝安中学高一理科数学(含答案)

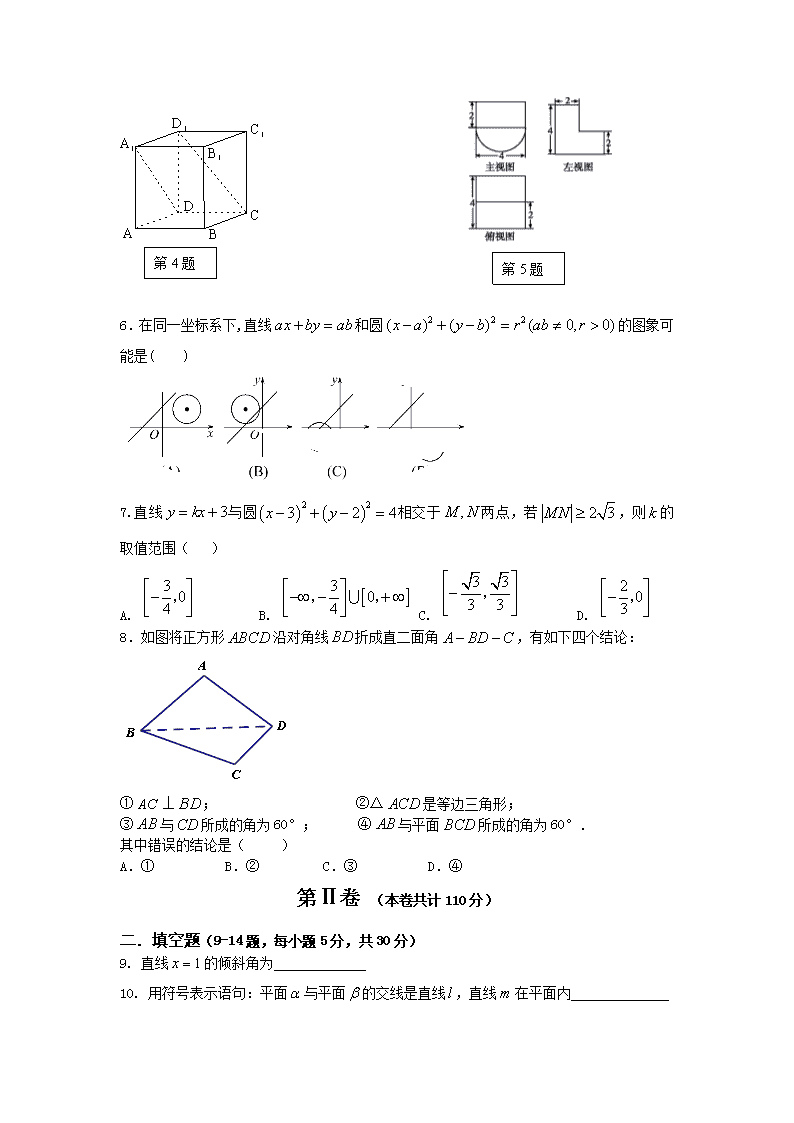
宝安中学2013－2014学年第二学期期中考试高一理科数学命题人：蔡毅审题人：许世清本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为1-8题，共40分，第Ⅱ卷为9-20题，共110分。全卷共计150分。考试时间为120分钟。注意事项：1、答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题纸上。2、第Ⅰ卷、第Ⅱ卷均完成在答题纸上。3、考试结束，监考人员将答题纸收回第Ⅰ卷（本卷共计40分）一．选择题（每小题只有一个选项，每小题5分，共计40分）1．sin13ocos17o+cos13osin17o化简得（）A．B．C．sin4oD．cos4o2．直线（为实常数）的倾斜角的大小是（）A．B．C．D．3．设，则（）A．B．C．D．4．如左下图，在正方体中，异面直线与所成的角为（）A．B．C．D．5．某几何体的三视图如右下图所示,则该几何体的体积为(　　)A．B．C．D．n第4题第5题6．在同一坐标系下,直线和圆的图象可能是(　　)7.直线与圆相交于两点，若，则的取值范围（）A.B.C.D.8．如图将正方形沿对角线折成直二面角，有如下四个结论：①⊥；②△是等边三角形；③与所成的角为60°；④与平面所成的角为60°．其中错误的结论是（）A．①B．②C．③D．④第Ⅱ卷（本卷共计110分）二．填空题（9-14题，每小题5分，共30分）9.直线的倾斜角为10.用符号表示语句：平面与平面的交线是直线，直线在平面内n11．过直线和的交点且与直线平行的直线方程为12．点到直线的距离的最大值是13．当直线l：y＝k(x－1)＋2被圆C：(x－2)2＋(y－1)2＝5截得的弦最短时，则k=________．14．如图，正方体ABCD—A1B1C1D1，则下列四个命题：①P在直线BC1上运动时，三棱锥A—D1PC的体积不变；②P在直线BC1上运动时，直线AP与平面ACD1所成角的大小不变；③P在直线BC1上运动时，二面角P—AD1—C的大小不变；④M是平面A1B1C1D1上到点D和C1距离相等的点，则M点的轨迹是过D1点的直线D1A1。其中真命题的编号是。三.解答题（15-20题，要求写出必要的解答或证明过程，共80分）15．已知，，求：(1)的值；(2)cos的值．16．如图，在棱长为的正方体中，点是棱的中点，点在棱上，且满足.（1）求证：；（2）求几何体的体积.n17．已知设函数（1）当,求函数的值域；（2）当时，若,求函数的值；18.如图，矩形的两条对角线相交于点，边所在直线的方程为,点在边所在直线上．（1）求边所在直线的方程；（2）求矩形外接圆的方程；（3）过点的直线与矩形的外接圆相交于两点，求19.如图，三棱锥中，底面，，，为的中点，为的中点，点在上，且.（1）求证：平面；（2）求证：三棱锥的体积.（3）求与平面所成角.20．已知圆.（1）若圆的切线在轴和轴上的截距相等，且截距不为零，求此切线的方程；（2）从圆外一点向该圆引一条切线，切点为，为坐标原点，且有，求使的长取得最小值的点的坐标.(3)直线与圆相交于两点，点为线段的三等分点，求直线的方程n宝安中学2013－2014学年第二学期期中考试高一理科数学参考答案一、选择题12345678BDACADAD二、填空题9、10、11、12、2+13、114、①③④三、解答题15、解：(1)因为tanα＝，所以tan2α＝.(2)因为α∈，所以2α∈(0，π)．又tan2α>0，所以sin2α＝，cos2α＝.所以cos＝cos2αcos-sin2αsin=.16、解：（1）连接，由于为正方体，所以四边形为正方形，所以，且平面，，，平面，平面，；（2）连接交于点，由于为正方体，，，，所以四边形为平行四边形，，由（1）知，平面，所以平面，平面，由，，在直角梯形中，直角腰，上底，下底，因此梯形的面积，n因此几何体的体积.17、解：（Ⅰ）由，得，时，函数的值域为（Ⅱ）,；所以=18、解：（I）因为边所在直线的方程为，且与垂直，所以直线的斜率为．又因为点在直线上，所以边所在直线的方程为,即．（II）由解得点的坐标为，因为矩形两条对角线的交点为．所以为矩形外接圆的圆心．又．从而矩形外接圆的方程为．（III）过点作圆的切线，切点为，则=819.（1）取的中点，的中点，连接，∵为中点，，∴.n∵面面，∴面.同理可证：面.又，∴面面.∵，∴面.（2）∵底面，且底面，∴由，可得又，∴平面平面，∴,为中点，∴，∴平面又由已知可得.∴所以三棱锥的体积为.(3).又，,,由于为中点，所以点到面的距离为点到面的距离的,则与平面所成角为20、解（1）切线在两坐标轴上的截距相等且截距不为零，∴设切线方程为（），又圆C：，∴圆心C到切线的距离等于圆的半径，∴，解得或，故所求切线的方程为：或．（2）设，切线与半径垂直，∴，∴，整理得，故动点在直线上，由已知的最小值就是的最小值，而的最小值为到直线的距离，n∴解得∴所求点坐标为．(3)①若直线的斜率不存在，则，此时直线与圆交于，易知点为的三等分点，符合题意；②若直线的斜率存在，设，不妨设为靠近点的三等分点。取线段的中点，且记弦长为，圆心到直线的距离为在直角三角形中：,即；在直角三角形中：,即所以，可得：