云南省腾冲市第八中学2018_2019学年高二数学下学期期中试题文

云南省腾冲市第八中学2018_2019学年高二数学下学期期中试题文

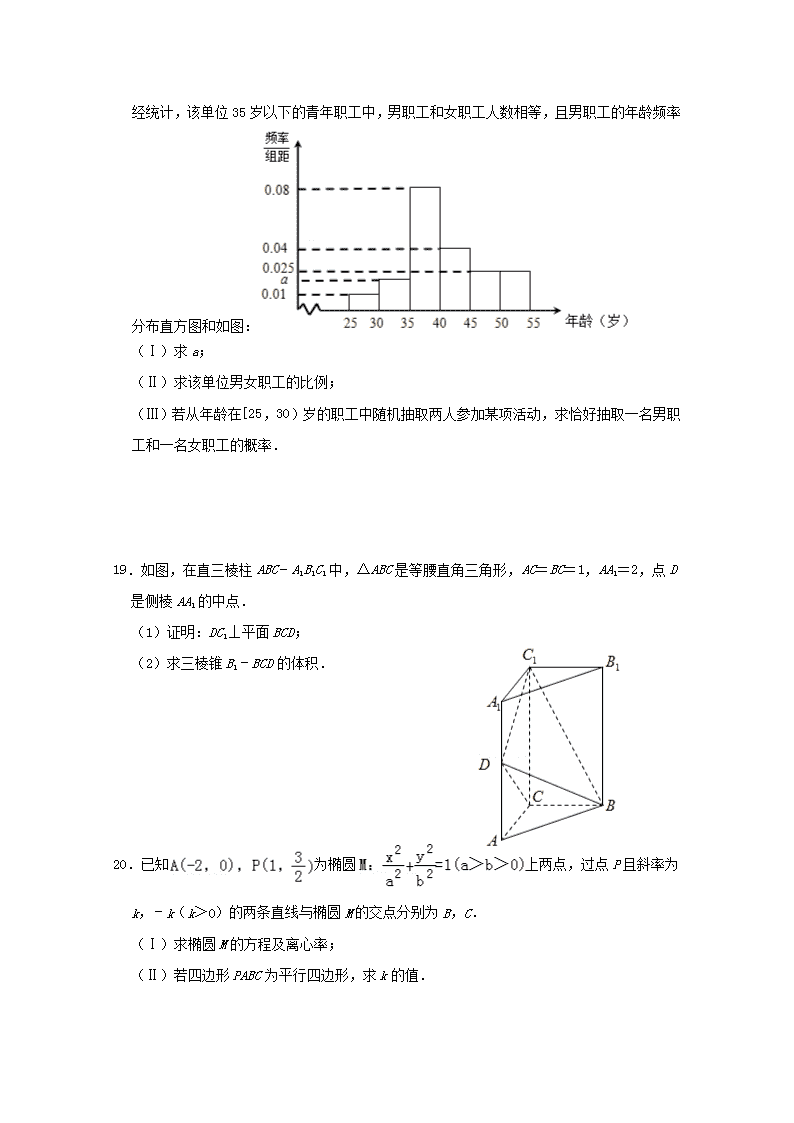
腾八中2018—2019学年度高二下学期期中考试文科数学试卷考试时间：120分钟，总分150分一．选择题（共12小题）1．已知全集U＝{x||x|＜2}，集合P＝{x|log2x＜1}，则∁UP＝（　　）A．（﹣2，0]B．（﹣2，1]C．（0，1）D．[1，2）2．若log2a＝0.3，0.3b＝2，c＝0.32，则实数a，b，c之间的大小关系为（　　）A．a＞b＞cB．a＞c＞bC．c＞a＞bD．b＞a＞c3．一个几何体的三视图如图所示，则该几何体的表面积为（　　）A．2B．C．2D．24．函数f（x）＝x2﹣6x+2ex的极值点所在区间为（　　）A．（0，1）B．（﹣1，0）C．（1，2）D．（﹣2，﹣1）5．如图所示，三国时代数学家在《周脾算经》中利用弦图，给出了勾股定理的绝妙证明．图中包含四个全等的直角三角形及一个小正方形（阴影），设直角三角形有一个内角为30°，若向弦图内随机抛掷200颗米粒（大小忽略不计，取），则落在小正方形（阴影）内的米粒数大约为（　　）A．20B．27C．54D．646．已知向量、的夹角为，且，，则＝（　　）A．B．10C．D．267．已知等比数列{an}的各项均为正数，且3a1，，2a2成等差数列，则＝（　　）A．1B．3C．6D．98．若x、y满足，则目标函数f＝x+2y的最大值为（　　）A．1B．2C．3D．49．△ABC中，（a﹣b）（sinA+sinB）＝（c﹣b）sinC．其中a，b，c分别为内角A，B，C的对边，则A＝（　　）nA．B．C．D．10．已知定义在R上的函数f（x）的导函数为f'（x），若f（x）+f'（x）＜0，f（0）＝1，则不等式exf（x）＜1的解集为（　　）A．（﹣∞，0）B．（0，+∞）C．（﹣∞，1）D．（1，+∞）11．设函数，曲线f（x）在（1，f（1））处的切线方程是（　　）A．5x﹣y﹣4＝0B．3x﹣y﹣2＝0C．x﹣y＝0D．x＝112．已知点P是椭圆E：＝1上的任意一点，AB是圆C：（x﹣2）2+y2＝4的一条直径，则的最大值是（　　）A．32B．36C．40D．48二．填空题（共4小题）13．以直角坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点A的极坐标为，则点A的直角坐标为　　．14．实数x，y满足3x2+4y2＝12，则2x+y的最大值　　．15．曲线上的点到直线的最大距离为　　．16．若函数f（x）＝1+|x|+，则f（lg2）+f（lg）+f（lg5）+f（lg）＝　　．三．解答题（共6小题）17．已知等比数列{an}的首项为2，等差数列{bn}的前n项和为Sn，且a1+a2＝6，2b1+a3＝b4，S3＝3a2．（Ⅰ）求{an}，{bn}的通项公式；（Ⅱ）设，求数列{cn}的前n项和．18．已知某单位全体员工年龄频率分布表为：年龄（岁）[25，30）[30，35）[35，40）[40，45）[45，50）[50，55）合计人数（人）61850311916140n经统计，该单位35岁以下的青年职工中，男职工和女职工人数相等，且男职工的年龄频率分布直方图和如图：（Ⅰ）求a；（Ⅱ）求该单位男女职工的比例；（Ⅲ）若从年龄在[25，30）岁的职工中随机抽取两人参加某项活动，求恰好抽取一名男职工和一名女职工的概率．19．如图，在直三棱柱ABC﹣A1B1C1中，△ABC是等腰直角三角形，AC＝BC＝1，AA1＝2，点D是侧棱AA1的中点．（1）证明：DC1⊥平面BCD；（2）求三棱锥B1﹣BCD的体积．20．已知为椭圆上两点，过点P且斜率为k，﹣k（k＞0）的两条直线与椭圆M的交点分别为B，C．（Ⅰ）求椭圆M的方程及离心率；（Ⅱ）若四边形PABC为平行四边形，求k的值．n21．已知函数f（x）＝lnx﹣ax（a∈R）．（Ⅰ）当a＝2时，求f（x）在点（1，f（1））处的切线方程；（Ⅱ）若对于任意的x∈（0，+∞），都有f（x）＜0，求a的取值范围．22．已知在平面直角坐标系xOy中，直线l1的参数方程为，圆C的参数方程为．（1）求直线l1与圆C的普通方程；（2）已知动点P在圆C上，动点Q在直线l2：x﹣y﹣2＝0上，求线段PQ的取值范围.n高二期中考试数学试卷参考答案与试题解析一．选择题（共13小题）1．已知全集U＝{x||x|＜2}，集合P＝{x|log2x＜1}，则∁UP＝（　　）A．（﹣2，0]B．（﹣2，1]C．（0，1）D．[1，2）【解答】解：∵全集U＝{x||x|＜2}＝（﹣2，2），集合P＝{x|log2x＜1}＝（0，2）∴∁UP＝（﹣2，0]故选：A．2．若log2a＝0.3，0.3b＝2，c＝0.32，则实数a，b，c之间的大小关系为（　　）A．a＞b＞cB．a＞c＞bC．c＞a＞bD．b＞a＞c【解答】解：a＝20.3＞20＝1，b＝log0.32＜log0.31＝0，0＜0.32＜1；∴a＞c＞b．故选：B．3．一个几何体的三视图如图所示，则该几何体的表面积为（　　）A．2B．C．2D．2【解答】解：由题意，几何体的直观图如图，是正方体的一部分，四棱锥P﹣ABCD，几何体的表面积为：1×1+＝2+．故选：C．n4．函数f（x）＝x2﹣6x+2ex的极值点所在区间为（　　）A．（0，1）B．（﹣1，0）C．（1，2）D．（﹣2，﹣1）【解答】解：f′（x）＝2x﹣6+2ex，∴f′（1）＝2﹣6+2e＞0，f′（0）＝﹣6+2＜0，由f'（0）f'（1）＜0，故f（x）的极值点所在的区间为（0，1），故选：A．5．如图所示，三国时代数学家在《周脾算经》中利用弦图，给出了勾股定理的绝妙证明．图中包含四个全等的直角三角形及一个小正方形（阴影），设直角三角形有一个内角为30°，若向弦图内随机抛掷200颗米粒（大小忽略不计，取），则落在小正方形（阴影）内的米粒数大约为（　　）A．20B．27C．54D．64【解答】解：设大正方体的边长为x，则小正方体的边长为﹣x，设落在小正方形内的米粒数大约为N，则＝，解得：N≈27故选：B．6．已知向量、的夹角为，且，，则＝（　　）A．B．10C．D．26n【解答】解：向量、的夹角为，且，，则＝＝＝．故选：A．7．已知等比数列{an}的各项均为正数，且3a1，，2a2成等差数列，则＝（　　）A．1B．3C．6D．9【解答】解：设等比数列{an}的公比为q，则∵各项均为正数的等比数列{an}，3a1，，2a2成等差数列，∴a3＝2a2+3a1，∴q2﹣2q﹣3＝0，∵q＞0，∴q＝3，＝q2＝9故选：D．8．若x、y满足，则目标函数f＝x+2y的最大值为（　　）A．1B．2C．3D．4【解答】解：作出不等式组对应的平面区域，由z＝x+2y，得y＝﹣x+，平移直线y＝﹣x+，由图象可知当直线经过点A时，直线y＝﹣x+的截距最小，此时z最小，由，得A（1，1）此时z＝1+2×1＝3．故选：C．n9．△ABC中，（a﹣b）（sinA+sinB）＝（c﹣b）sinC．其中a，b，c分别为内角A，B，C的对边，则A＝（　　）A．B．C．D．【解答】解：∵（a﹣b）（sinA+sinB）＝（c﹣b）sinC，由正弦定理可得，（a﹣b）（a+b）＝（c﹣b）c，化简可得，b2+c2﹣a2＝bc，由余弦定理可得，cosA＝＝∵0＜A＜π∴A＝故选：B．10．已知定义在R上的函数f（x）的导函数为f'（x），若f（x）+f'（x）＜0，f（0）＝1，则不等式exf（x）＜1的解集为（　　）A．（﹣∞，0）B．（0，+∞）C．（﹣∞，1）D．（1，+∞）【解答】解：根据题意，令g（x）＝exf（x），其导数g′（x）＝exf（x）+exf′（x）＝ex[f′（x）+f（x）]，又由对于任意实数x有f′（x）+f（x）＜0，则有g′（x）＝ex[f′（x）+f（x）]＜0，即函数g（x）在R上为减函数，又由f（0）＝1，则g（0）＝e0f（0）＝1，则exf（x）＜1⇒g（x）＜g（0），又由函数g（x）在R上为减函数，则有x＞0，即不等式exf（x）＜1的解集为（0，+∞）；n故选：B．11．设函数，曲线f（x）在（1，f（1））处的切线方程是（　　）A．5x﹣y﹣4＝0B．3x﹣y﹣2＝0C．x﹣y＝0D．x＝1【解答】解：由，得f（1）＝f′（）﹣2，由，得f′（x）＝，取x＝，可得f′（）＝f′（）﹣2+2f（1），f（1）＝1，代入f（1）＝f′（）﹣2，得f′（）＝3，∴f（x）＝3x2﹣2x+lnx，则f′（x）＝6x﹣2+．∴f′（1）＝5，∴曲线f（x）在（1，f（1））处的切线方程是y﹣1＝5（x﹣1），即5x﹣y﹣4＝0．故选：A．12．已知点P是椭圆E：＝1上的任意一点，AB是圆C：（x﹣2）2+y2＝4的一条直径，则的最大值是（　　）A．32B．36C．40D．48【解答】解：如图所示，设P（x，y），满足＝1．＝，＝，＝，＝﹣R2＝﹣4，∴＝（）•（）＝+•（）+＝﹣4，＝（x﹣2）2+y2﹣4＝（x﹣2）2+﹣4＝﹣4，﹣4≤x≤4．∴当且仅当x＝﹣4时，﹣4＝32．n∴的最大值是32．故选：A．二．填空题（共4小题）13．以直角坐标原点为极点，x轴的正半轴为极轴建立极坐标系，点A的极坐标为，则点A的直角坐标为　（1，）　．【解答】解：∵点A的极坐标为，∴x＝2cos＝1，y＝2sin＝，∴点A的直角坐标为（1，）．故答案为：（1，）．14．实数x，y满足3x2+4y2＝12，则2x+y的最大值　5　．【解答】解：根据题意，实数x，y满足3x2+4y2＝12，即+＝1，设x＝2cosθ，y＝sinθ，则2x+y＝4cosθ+3sinθ＝5sin（θ+α），（tanα＝），又由﹣1≤5sin（θ+α）≤1，则﹣5≤2x+y≤5，即2x+y的最大值5；故答案为：5．15．曲线上的点到直线的最大距离为　　．n【解答】解：设曲线上的点P（4cosθ，2sinθ），则曲线上的点到直线的距离：d＝＝，∴当sin（）＝﹣1时，曲线上的点到直线的最大距离为：＝．故答案为：．16．若函数f（x）＝1+|x|+，则f（lg2）+f（lg）+f（lg5）+f（lg）＝　6　．【解答】解：f（x）＝1+|x|+，∴f（﹣x）+f（x）＝2+2|x|，∵lg＝﹣lg2，lg＝﹣lg5，∴f（lg2）+f（lg）+f（lg5）+f（lg）＝2×2+2（lg2+lg5）＝6，故答案为：6三．解答题（共6小题）17．已知等比数列{an}的首项为2，等差数列{bn}的前n项和为Sn，且a1+a2＝6，2b1+a3＝b4，S3＝3a2．（Ⅰ）求{an}，{bn}的通项公式；（Ⅱ）设，求数列{cn}的前n项和．【解答】解：（Ⅰ）设数列{an}的公比为q，数列{bn}的公差为d．由a1+a2＝6，得a1+a1q＝6．因为a1＝2，所以q＝2．所以．由得解得所以bn＝b1+（n﹣1）d＝3n﹣2．………..（8分）（Ⅱ）由（Ⅰ）知，bn＝3n﹣2．n所以．从而数列{cn}的前n项和＝＝6×2n﹣2n﹣6．．（13分）18．已知某单位全体员工年龄频率分布表为：年龄（岁）[25，30）[30，35）[35，40）[40，45）[45，50）[50，55）合计人数（人）61850311916140经统计，该单位35岁以下的青年职工中，男职工和女职工人数相等，且男职工的年龄频率分布直方图和如图：（Ⅰ）求a；（Ⅱ）求该单位男女职工的比例；（Ⅲ）若从年龄在[25，30）岁的职工中随机抽取两人参加某项活动，求恰好抽取一名男职工和一名女职工的概率．【解答】（本小题13分）解：（Ⅰ）由男职工的年龄频率分布直方图可得：（a+0.01+0.04+0.08+0.025+0.025）×5＝1．所以a＝0.02．（Ⅱ）该单位[25，35）岁职工共24人，由于[25，35）岁男女职工人数相等，所以[25，35）岁的男职工共12人．由（Ⅰ）知，男职工年龄在[25，35）岁的频率为0.15，所以男职工共有人，所以女职工有140﹣80＝60人，所以男女比例为4：3．（Ⅲ）由男职工的年龄频率分布直方图可得：男职工年龄在[25，30）岁的频率为0.05．n由（Ⅱ）知，男职工共有80人，所以男职工年龄在[25，30）岁的有4人，分别记为A1，A2，A3，A4．又全体员工年龄在[25，30）岁的有6人，所以女职工年龄在[25，30）岁的有2人，分别记为B1，B2．从年龄在25～30岁的职工中随机抽取两人的结果共有（A1，A2），（A1，A3），（A1，A4），（A1，B1），（A1，B2），（A2，A3），（A2，A4），（A2，B1），（A2，B2），（A3，A4），（A3，B1），（A3，B2），（A4，B1），（A4，B2），（B1，B2）15种情况，其中一男一女的有（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2），（A4，B1），（A4，B2）8种情况，所以恰好抽取一名男职工和一名女职工的概率为．19．如图，在直三棱柱ABC﹣A1B1C1中，△ABC是等腰直角三角形，AC＝BC＝1，AA1＝2，点D是侧棱AA1的中点．（1）证明：DC1⊥平面BCD；（2）求三棱锥B1﹣BCD的体积．【解答】（1）证明：∵ACC1A1是矩形，且AC＝1，AA1＝2，D是棱AA1的中点，∴△DAC，△DA1C1均为等腰直角三角形，∴DC1⊥DC．又∵BC⊥侧面AC1，∴BC⊥DC1．又∵BC∩DC＝C，BC，CD⊂面BCD，∴DC1⊥平面BCD；（2）解：∵B1C1∥BC，且BC⊂面BCD，B1C1⊄面BCD，∴B1C1∥面BCD．∴＝．n20．已知为椭圆上两点，过点P且斜率为k，﹣k（k＞0）的两条直线与椭圆M的交点分别为B，C．（Ⅰ）求椭圆M的方程及离心率；（Ⅱ）若四边形PABC为平行四边形，求k的值．【解答】（共13分）解：（I）由题意得解得所以椭圆M的方程为．又，所以离心率．………………………..（5分）（II）设直线PB的方程为y＝kx+m（k＞0），由消去y，整理得（3+4k2）x2+8kmx+（4m2﹣12）＝0．当△＞0时，设B（x1，y1），C（x2，y2），则，即．将代入y＝kx+m，整理得，所以．n所以．所以．同理．所以直线BC的斜率．又直线PA的斜率，所以PA∥BC．因为四边形PABC为平行四边形，所以|PA|＝|BC|．所以，解得或.时，B（﹣2，0）与A重合，不符合题意，舍去．所以四边形PABC为平行四边形时，．………………………………（13分）21．已知函数f（x）＝lnx﹣ax（a∈R）．（Ⅰ）当a＝2时，求f（x）在点（1，f（1））处的切线方程；（Ⅱ）若对于任意的x∈（0，+∞），都有f（x）＜0，求a的取值范围．【解答】解：（Ⅰ）当a＝2时，f（x）＝lnx﹣2x，∴f′（x）＝，则f′（1）＝﹣1，又f（1）＝﹣2，∴f（x）在点（1，f（1））处的切线方程为y+2＝﹣（x﹣1），即x+y+1＝0；（Ⅱ）f（x）的定义域为（0，+∞），f′（x）＝．当a≤0时，f′（x）＞0，f（x）在（0，+∞）上单调递增，又f（1）＝﹣a≥0，不合题意；当a＞0时，当0＜x＜时，f′（x）＞0，f（x）单调递增；当x＞时，f′（x）＜0，f（x）单调递减．∴函数f（x）在x＝时求得最大值为f（）＝ln﹣1．n∵对于任意的x∈（0，+∞），都有f（x）＜0，∴直线＜0，即a＞．∴a的取值范围是（）．22．已知在平面直角坐标系xOy中，直线l1的参数方程为，圆C的参数方程为．（1）求直线l1与圆C的普通方程；（2）已知动点P在圆C上，动点Q在直线l2：x﹣y﹣2＝0上，求线段PQ的取值范围．【解答】解：（1）由消去参数t得2x﹣y+4＝0；由消去θ得x2+（y﹣2）2＝4；