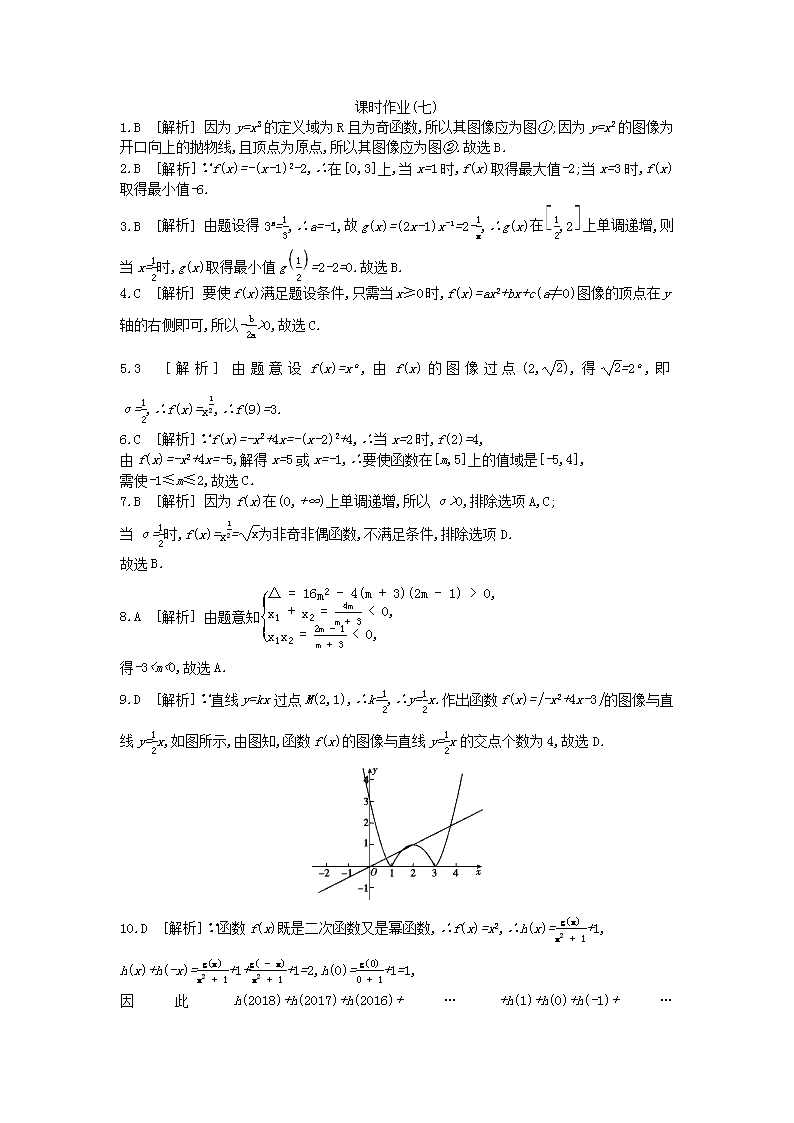2020版高考数学复习第二单元第7讲二次函数与幂函数练习文(含解析)新人教a版
第7讲 二次函数与幂函数1.如图K7-1所示给出了4个幂函数的大致图像,则图像与函数对应正确的是( )图K7-1A.①y=x13,②y=x2,③y=x12,④y=x-1B.①y=x3,②y=x2,③y=x12,④y=x-1C.①y=x2,②y=x3,③y=x12,④y=x-1D.①y=x13,②y=x12,③y=x2,④y=x-12.函数f(x)=-x2+2x-3在[0,3]上的最大值、最小值分别为( )A.0,-2B.-2,-6C.-2,-3D.-3,-63.[2018·茂名联考]已知幂函数f(x)=xa的图像过点3,13,则函数g(x)=(2x-1)f(x)在区间12,2上的最小值是( )A.-1B.0C.-2D.324.定义域为R的函数f(x)=ax2+b|x|+c(a≠0)有两个极值,则实数a,b,c满足( )A.b2-4ac>0且a>0B.b2-4ac>0C.-b2a>0D.-b2a<05.已知幂函数f(x)的图像过点(2,2),则f(9)= . 6.[2018·西安联考]已知函数f(x)=-x2+4x,x∈[m,5]的值域是[-5,4],则实数m的取值范围是( )A.(-∞,-1)B.(-1,2]C.[-1,2]D.[2,5]7.[2018·合肥三检]已知α∈-1,2,12,3,13,若f(x)=xα为奇函数,且在(0,+∞)上单调递增,则实数α的值是( )A.-1,3B.13,3C.-1,13,3D.13,12,3n8.关于x的二次方程(m+3)x2-4mx+2m-1=0的两个根异号,且负根的绝对值比正根大,那么实数m的取值范围是( )A.-3
0D.m<0或m>39.若函数f(x)=|-x2+4x-3|的图像与直线y=kx相交于点M(2,1),则函数f(x)的图像与该直线的交点个数为( )A.1B.2C.3D.410.[2018·保定模拟]已知函数f(x)既是二次函数又是幂函数,函数g(x)是R上的奇函数,函数h(x)=g(x)f(x)+1+1,则h(2018)+h(2017)+h(2016)+…+h(1)+h(0)+h(-1)+…+h(-2016)+h(-2017)+h(-2018)=( )A.0B.2018C.4036D.403711.已知a=2-32,b=253,c=123,则a,b,c的大小关系是 . 12.[2018·岳阳一中模拟]已知f(x)=-(x-a)2,x≥0,-x2-2x-3+a,x<0,若∀x∈R,f(x)≤f(0)恒成立,则实数a的取值范围为 . 13.已知幂函数y=xm2-2m-3(m∈N*)的图像关于y轴对称,且在(0,+∞)上是减函数,求满足(a+1)-m3<(3-2a)-m3的a的取值范围.14.已知二次函数f(x)=x2+2bx+c(b,c∈R).(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b,c的值;(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2),(0,1)上,求实数b的取值范围.15.[2018·东北师大附中月考]对于函数f(x),若存在x0∈R,使得f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+b-1(a≠0).(1)当a=1,b=-2时,求f(x)的不动点;(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.n课时作业(七)1.B [解析]因为y=x3的定义域为R且为奇函数,所以其图像应为图①;因为y=x2的图像为开口向上的抛物线,且顶点为原点,所以其图像应为图②.故选B.2.B [解析]∵f(x)=-(x-1)2-2,∴在[0,3]上,当x=1时,f(x)取得最大值-2;当x=3时,f(x)取得最小值-6.3.B [解析]由题设得3a=13,∴a=-1,故g(x)=(2x-1)x-1=2-1x,∴g(x)在12,2上单调递增,则当x=12时,g(x)取得最小值g12=2-2=0.故选B.4.C [解析]要使f(x)满足题设条件,只需当x≥0时,f(x)=ax2+bx+c(a≠0)图像的顶点在y轴的右侧即可,所以-b2a>0,故选C.5.3 [解析]由题意设f(x)=xα,由f(x)的图像过点(2,2),得2=2α,即α=12,∴f(x)=x12,∴f(9)=3.6.C [解析]∵f(x)=-x2+4x=-(x-2)2+4,∴当x=2时,f(2)=4,由f(x)=-x2+4x=-5,解得x=5或x=-1,∴要使函数在[m,5]上的值域是[-5,4],需使-1≤m≤2,故选C.7.B [解析]因为f(x)在(0,+∞)上单调递增,所以α>0,排除选项A,C;当α=12时,f(x)=x12=x为非奇非偶函数,不满足条件,排除选项D.故选B.8.A [解析]由题意知Δ=16m2-4(m+3)(2m-1)>0,x1+x2=4mm+3<0,x1x2=2m-1m+3<0,得-3c>b [解析]a=2-32=223,根据函数y=x3是R上的增函数,且22>12>25,得223>123>253,即a>c>b.12.[-2,0] [解析]若∀x∈R,f(x)≤f(0),则f(x)max=f(0)=-a2.当x≥0时,f(x)=-(x-a)2,此时函数图像的对称轴方程为x=a≤0;当x<0时,f(x)=-x2-2x-3+a,其图像开口向下,对称轴方程为x=-1,则f(-1)=-1+2-3+a≤-a2,即a2+a-2≤0,解得-2≤a≤1.综上所述,实数a的取值范围是[-2,0].13.解:∵幂函数在(0,+∞)上是减函数,∴m2-2m-3<0,解得-13-2a>0或0>a+1>3-2a或a+1<0<3-2a,解得a<-1或230,g(-2)=1-5b<0,g(0)=-1-b<0,g(1)=b+1>0,解得150(b∈R)恒成立.设g(b)=b2-4ab+4a,若g(b)>0恒成立,则Δ=(4a)2-16a<0,解得0
查看更多