- 2022-02-12 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级数学教案《《圆的面积练习》
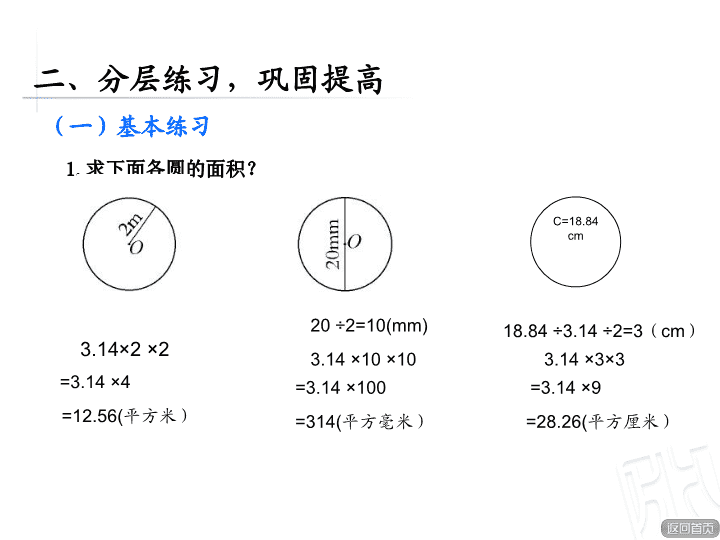
圆的面积练习 梳理总结,提升认识 分层练习,巩固提高 问题回顾,再现新知 运动会报名 一、问题回顾,再现新知 已知 圆的 周长 , 如何计算圆的面积? 已知 圆的半径 , 如何计算圆的面积? 已知 圆的 直 径 , 如何计算圆的面积? 已知 半径 求圆的面积公式: S=π 已知 直径 求圆的面积公式: r=d÷2 , S=π 。 已知 周长 求圆的面积公式: r=C÷2π , S=π 。 二、分层练习,巩固提高 ( 一)基本练习 1. 求下面各圆的面积? C=18.84cm 3.14 × 2 × 2 =3.14 × 4 =12.56( 平方米) 20 ÷ 2=10(mm) 3.14 × 10 × 10 =3.14 × 100 =314( 平方毫米) 18.84 ÷ 3.14 ÷ 2=3 ( cm ) 3.14 × 3 × 3 =3.14 × 9 =28.26( 平方厘米) 二、分层练习,巩固提高 (二)综合练习 2. 这个自动旋转喷水器的喷灌面积是多少平方米? 3.14 × 8 × 8 =3.14 × 64 =200.96( 平方米) 求喷灌面积实际是求圆的面积, 8 米 是圆的半径 。 答:这个自动旋转喷水器的喷灌面积是 200.96 平方米。 二、分层练习,巩固提高 (二)综合练习 3. ①如果要给圆桌铺上同样大小的玻璃,这块玻璃的面积是多少平方米 ? 3.14 × 1 × 1 =3.14 × 1 =3.14( 平方米) 求玻璃的面积实际也是求 直径为 2 米的 圆的面积 。 答:这块玻璃的面积是 3.14 平方米。 2 ÷ 2=1(m) 二、分层练习,巩固提高 (二)综合练习 3 . ②如果在圆桌的周围镶上金属条,需要多少米? 3.14 × 2 =6.28( 米) 求圆桌的周围的金属条实际是求 直径为 2 米的 圆的周长 。 答:这块玻璃的面积是 3.14 平方米。 小结:求圆的面积和求圆的周长的公式不同,在解决问题的时候一定分析清楚,求的是什么。 二、分层练习,巩固提高 (三)拓展练习 4 . 用一个长方形铁板切割成一个最大的圆, 圆的面积是多少平方米?剩下的部分是多少 平方米? 2 ÷ 2=1(m) “最大” 的圆的 直径应该与长方形的宽是一样大小,即圆的直径就是 2 米。 答 :圆的面 积是 3.14 平方 米,剩下的部分是 2.86 平方米。 3.14 × 1 × 1 =3.14 × 1 =3.14( 平方米) 3 × 2=6 (平方米) 6-3.14=2.86 (平方米) 二、分层练习,巩固提高 (三)拓展练习 5. 清代一枚铜钱及其示意图,算出 示意图中涂色部分的面积。 涂色 部分的面积应该是用圆的面积减 去中间正方形的面积。 答 : 涂 色部分的面 积 是 6.425 平方厘米 。 3 ÷ 2=1.5 ( 厘米 ) 3.14 × 1.5 × 1.5 =3.14 × 2.25 =7.065( 平方厘米) 0.8 × 0.8=0.64 (平方厘米) 7.065-0.64=6.425 (平方厘米) 教师小结: 此题与 求圆环的面积类似,圆环的面积是大圆面积减小 圆面积,而这题是用大圆面积减中间正方形的面积,虽然图形发生 变化,但求解的方式方法没有变化。 二、分层练习,巩固提高 (三)拓展练习 30 ÷ 2=15( 米 ) 扩建后增加 了 半径 5 米与原来的圆形成了圆环,增加的面积就是圆环的面积 。 答 :扩建后旱冰场的面积增加了 549.5 平 方 米。 3.14 × 20 × 20-3.14 × 15 × 15 =3.14 × 400-3.14 × 225 =549.5( 平方米) 15+5=20 (米) 课堂总结 这节课我们学习了什么? 你有哪些收获? 还有什么问题?查看更多