六年级数学下册第三单元《啤酒生产中的数学—比例》教学课件青岛版六三制

六年级数学下册第三单元《啤酒生产中的数学—比例》教学课件青岛版六三制

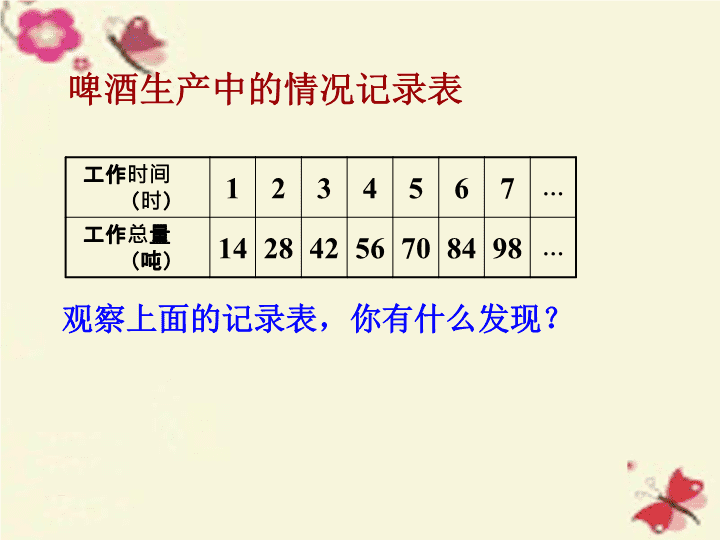
收获和付出是 成正比的。 啤酒生产中的数学 ——正比例 啤酒生产中的情况记录表 工作时间（时） 1 2 3 4 5 6 7 … 工作总量（吨） 14 28 42 56 70 84 98 … 观察上面的记录表，你有什么发现？ 工作总量 工作时间 = 工作效率（一定） 工作时间 变化 ，工作总量也随着 变化 ，工作效率 不变 ，也就是工作总量与工作时间的 比值一定 ，我们就说工作总量和工作时间是 成正比例的量 ，它们的关系叫做 正比例关系 。 正比例关系 工作时间（时） 1 2 4 5 6 7 … 工作总量（吨） 14 28 42 56 84 98 … 正比例关系 啤酒生产中的情况记录表 3 70 例 1 （ 1 ）正方形的边长和周长变化 如下表： 边长 5 8 10 12 20 周长 20 32 40 48 80 正方形的 周长 和 边长 成正比例吗？为什么？ （ 2 ）正方形的边长和周长及面积变化 如下表： 边长 5 8 10 12 20 周长 20 32 40 48 80 面积 25 64 100 144 400 正方形的 面积 和 边长 成正比例吗？为什么？ 1. 判断下面每题中两种量是不是成正比例，并说明理由。 （ 1 ）速度一定，路程和时间。 （ 2 ）一个人的年龄与体重。 （ 3 ）平行四边形的高一定，它的底与面积。 （ 4 ）天数一定，生产零件的总个数与每天生 产零件的个数。 练一练： 想一想，生活中还有哪两种量成正比例关系？ 已知 x 和 y 成正比例，请将下表填完整。 练一练： x 2 0.6 y 10 15 3 3 你能把工作时间和工作总量之间的关系在下图中表示出来吗？ 工作总量（吨） 工作时间（时） 1 2 3 4 5 6 7 14 28 42 56 70 84 98 0 （ 1 ）从图中你发现了什么？ 例 2 （ 2 ）根据上图估计一下， 4.5 小时大约能生产多少吨啤酒？ 工作总量（吨） 工作时间（时） 1 2 3 4 5 6 7 14 28 42 56 70 84 98 0 例 2 4.5 （ 3 ）估计一下，要生产 80 吨啤酒，大约需要多少小时？ 工作总量（吨） 工作时间（时） 1 2 3 4 5 6 7 14 28 42 56 70 84 98 0 例 2 80 路程（千米） 时间（时） 1 2 3 4 5 6 7 8 9 10 80 160 240 320 400 480 560 0 640 720 800 一辆汽车行驶的路程和时间之间的关系如下图。 练一练： （ 1 ）从图中你发现了什么？ 路程（千米） 时间（时） 1 2 3 4 5 6 7 8 9 10 80 160 240 320 400 480 560 0 640 720 800 （ 2 ）根据上图估计一下，要行驶 600 千米 大约需要多少小时？ 练一练： 一辆汽车行驶的路程和时间之间的关系如下图。 路程（千米） 时间（时） 1 2 3 4 5 6 7 8 9 10 80 160 240 320 400 480 560 0 640 720 800 （ 3 ）估计一下 8.5 小时大约行驶多少千米？ 一辆汽车行驶的路程和时间之间的关系如下图。 练一练： 达标检测 1. 在一定的弹性限度内，弹簧伸长的长度与所挂物体的质量情况如下表。 物体质量（ kg ） 1 2 3 4 5 6 7 弹簧伸长长度（ cm ） 0.5 1 1.5 2 2.5 3 3.5 （ 1 ）弹簧 伸长的长度 与 所挂物体的质量 成正比例关系吗？说明理由。 （ 2 ）在下图中描出表示物体质量和弹簧伸长长度相对应的点，然后把它们按顺序连接起来。 达标检测 物体质量（ kg ） 1 2 3 4 5 6 7 弹簧伸长长度（ cm ） 0.5 1 1.5 2 2.5 3 3.5 长度（厘米） 质量（千克） 1 2 3 4 5 6 7 0.5 1 1.5 2 2.5 3 3.5 0 （ 3 ）根据上图估计一下，称 2.5 千克物体时，弹簧大约伸长多少厘米？ 达标检测 长度（厘米） 质量（千克） 1 2 3 4 5 6 7 0.5 1 1.5 2 2.5 3 3.5 0 （ 4 ）如果已知弹簧原长 5cm ，那么挂上不同质量的物体时，弹簧总长度如下表。 物体质量（ kg ） 1 2 3 4 5 6 7 弹簧伸长长度（ cm ） 0.5 1 1.5 2 2.5 3 3.5 弹簧总长度（ cm ） 弹簧的 总长度 与 所挂物体的质量 成正比例关系吗？说明理由。 达标检测 8.5 5.5 8 7.5 7 6.5 6 人生成就的大小 总是和抱负的大小成正比 谢谢，再见！