- 2022-02-11 发布 |
- 37.5 KB |
- 7页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级数学教案《按比例分配问题》
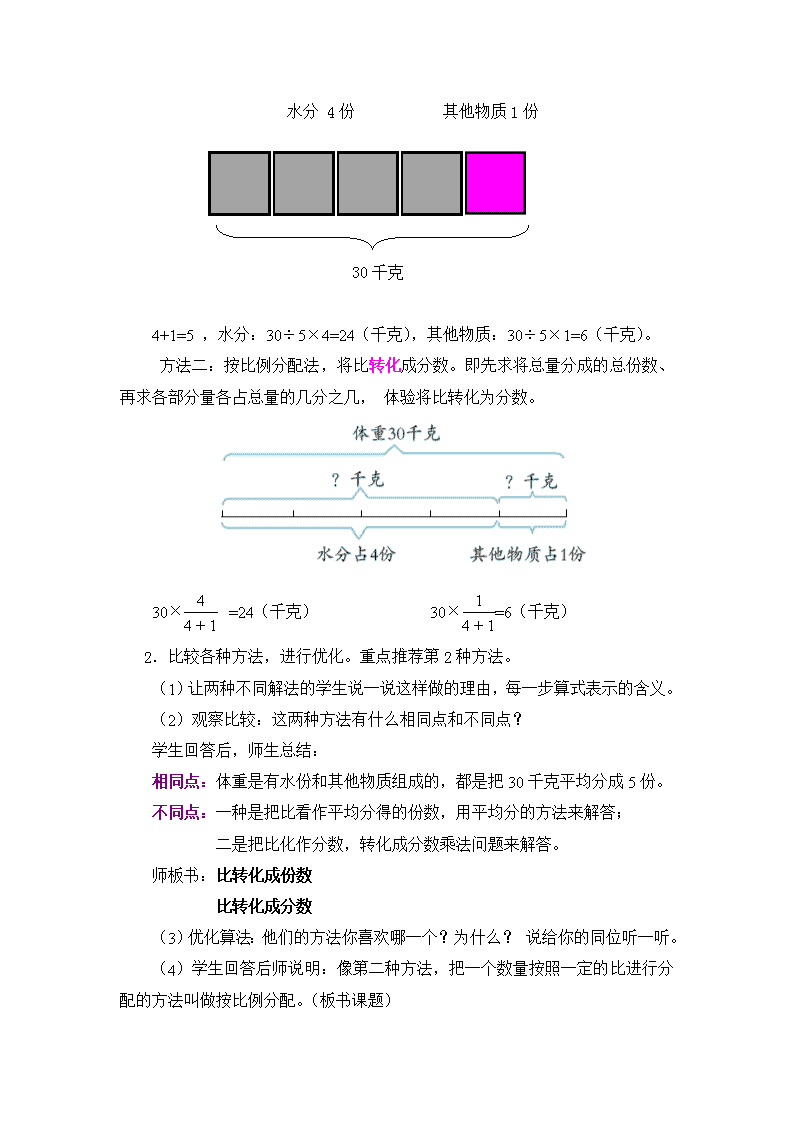
按比例分配问题 教学内容: 小学数学六年级(上册)第四单元信息窗2第45—46页的内容。 教学目标: 1.结合实际问题具体情境,理解按比例分配的意义。 2.掌握按比例分配的计算方法,并能较熟练地运用按比例分配的方法解决生活中的实际问题。 3.渗透转化的数学思想和方法,体验解决问题策略的多样性。 4.感受到数学与实际生活的密切联系,增强数学的应用意识。 教学重点: 按比例分配的计算方法,合理解决实际问题 教学难点: 理解按比例分配的意义;熟练合理解决实际问题。 教学准备:多媒体课件、尺子 教学过程: 一、 创设情境,提出问题 1.谈话:前几天我们学习了有关人体奥秘的知识,今天我们继续研究有关人体的知识。出示情境图。 请仔细观察情境图。(出示课件) 2.提问: 通过情境图你获得了哪些数学信息? (1)学生观察回答,教师适时板书相应的信息条件。 (2)根据这些信息你能提出哪些数学问题? 学生口答,教师板书学生提出的问题。 预设问题:①明明体内含的水分及其他物质有多少千克? ②爸爸体内含的水分及其他物质有多少千克? 3.板书课题,明确目标 如何解决这两个问题呢?这节课我们就来共同探究学习。首先请看本课的学习目标。 出示学习目标: 1.结合实际问题具体情境,理解按比例分配的意义。 2.掌握按比例分配的计算方法,并能较熟练地运用按比例分配的方法解决生活中的实际问题。 二、自主学习,小组探究 1.解决第一个问题:明明体内的水分及其他物质各有多少千克? (1)谈话:想解决这个问题?可以根据哪些数学信息? (体重30千克,体内水与其它物质的比是:4:1) (2)出示自学指导。 请大家仔细认真看课本第45页的内容,重点看线段图及方框里内容,思考: 1.体重30千克与4:1有什么联系? 2.方框内两种解决问题的方法一样吗?有何相同与不同? 想一想,算一算,可以画图帮自己思考,然后把你的想法、算法写出来,5分钟后看谁会做与例题类似的题目。 二、小组学习,自主探究 学生探究,师巡视辅导。 三 、汇报交流,评价质疑 1.展示学生的探究成果。请不同做法的学生到黑板板演并介绍,组织学生倾听与质疑,关键把每种方法解读清楚,让大家听明白。 预设解法: 解法一:归一法 画图法,水分占4份,其它物质占1份,先求1份,再求多份。体会将比转化为除法。 即:根据各部分量的比,先求出总份数,再求出每份数量,最后求出各部分数量。 水分 4份 其他物质1份 30千克 4+1=5 ,水分:30÷5×4=24(千克),其他物质:30÷5×1=6(千克)。 方法二:按比例分配法,将比转化成分数。即先求将总量分成的总份数、再求各部分量各占总量的几分之几, 体验将比转化为分数。 30×=24(千克) 30×=6(千克) 2.比较各种方法,进行优化。重点推荐第2种方法。 (1)让两种不同解法的学生说一说这样做的理由,每一步算式表示的含义。 (2)观察比较:这两种方法有什么相同点和不同点? 学生回答后,师生总结: 相同点:体重是有水份和其他物质组成的,都是把30千克平均分成5份。 不同点:一种是把比看作平均分得的份数,用平均分的方法来解答; 二是把比化作分数,转化成分数乘法问题来解答。 师板书:比转化成份数 比转化成分数 (3)优化算法:他们的方法你喜欢哪一个?为什么? 说给你的同位听一听。 (4)学生回答后师说明:像第二种方法,把一个数量按照一定的比进行分配的方法叫做按比例分配。(板书课题) 3. 解决第二个问题:爸爸体内的水分和其他物质各有多少千克? (1)师:你能用这种方法解决第二个问题吗? (2)学生独立完成,同位交流自己的想法。 (3)派代表在班内交流,并说说如何做的。 四、总结概括,抽象提升 今天学习的按比例分配的问题,我们可以将比转化成份数,先求1份的量,再求多份的量,用除法做;也可以将比转换成分数,即先求部分量占总数量的几分之几,从分数的角度用乘法算。这两种方法都利用了转化的思想,转化是一种重要的数学思想,在我们以后的学习中也会经常用到。 五、巩固应用,拓展延伸 (一)基本练习 1.一种糖水是糖与水按1:19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克? 找学生板演,其余练习,师巡视辅导:然后展示汇报,重点说思路及方法,并让学生养成验算的习惯。 2.学校修整校园用的混凝土是由2份水泥、3份石子和5份沙子混合成的。现在要用150吨混凝土,需要水泥、石子、沙子各多少吨? 找学生板演,其余练习,师巡视辅导,然后展示汇报,重点说思路及方法,交流时,多照顾暂时有困难的学生。让他们明白:先按照三个量的份数写出三个量的比,再按照按比例分配的思路解答,分配三个量和两个量的解题思路及方法是相同的。 (二) 变式练习(自主练习46页第7题) 某市举行小学生“卡拉OK”比赛,对进入决赛的选手安2:3的比例评出一、二等奖。如果获二等奖的有21名选手,获一等奖的选手有多少名? 找学生板演,其余练习,做题前让学生分析比较此题目和前面题目不一样的地方,然后独立思考,解决问题。做完后让学生说解题思路。 预设以下两种情况: 第一种按2:3评出“一、二等奖”转化为一等奖的人数是二等奖的或二等奖是一等奖的。 第二种根据二等奖的人数和所占比例,先求出每份的人数,再求获一等奖的人数。 (三)拓展延伸(补充题) 合理搭配早餐。 小明今天的早餐表 面包 鸡蛋 牛奶 100克 50克 200克 (1)小明今天的早餐是按怎样的比搭配的? (2)如果小明的妈妈按同样的比准备420克早餐,算算各种食物分别需要多少克? 找学生板演,然后共同订正,并说说解题思路。 六、全课总结 通过这节课的学习你有哪些收获? 根据学生的回答,老师小结:通过学习我们知道了按比例分配在我们生活中的应用非常广泛,比如在建筑业、农业、医药、国防等方面都需要非常精确地应用按比例分配的知识,所以同学们今后要留心观察生活,并会运用所学的知识来解决生活中的实际问题。 板书设计: 按 比 例 分 配 方法一 :比转化成份数 4+1=5 30÷5×4=24(千克) 30÷5×1=6(千克) 方法二: 比转化成分数 30×=24(千克) 30×=6(千克) 使用说明: 1.设计说明: (1)巧创情,智激趣。 上课开始运用了真实的情境,让学生感觉到比的应用就在我们身边,按比分配也存在于日常生活中,拉近了学生与新知的距离,学生积极踊跃的提出问题,独立解决问题、交流各自的方法、概括归纳出按比例分配的算理,充分展现了学生的思维,有效地调动了学生的学习积极性。 (2) 多样化的算法,多角度的思维。 在教学人体奥秘的问题时,我鼓励学生开拓思路,大胆思维,用尽可能多的方法去解决此问题,学生可以将比转化成份数,先求1份量,再求多份量,用除法做;也可以将比转换成分数,即先求部分量占总数量的几分之几?从分数的角度用乘法算。在教学中,我给学生充分的思维空间和选择余地,激励学生去发现、去创新,展示不同的解题思路,注重算法的多样化,鼓励学生能够从不同的角度解决问题。 (3) 做学结合,渗透方法。 “知识的获得是一个主动的过程”。做中学,学中做,注重数学思想方法的渗透。本课我充分发挥教师的主导作用,突出学生的主体地位,没有占用过多的时间去讲解,而是有重点地进行点拨和引导。整节课密度大、容量大。自主学习、合作学习、教师点拨相辅相成。教学中我不仅注重知识的传授,而且更注重数学思想方法的渗透,帮助学生在交流的过程中真正理解和掌握基本的数学知识与技能。 2.使用建议:在教学时,教师要给学生充分的思维空间和选择余地,激励学生去发现、去创新,展示不同的解题思路,最后,教师归纳总结出按比例分配法,一是把比看作平均分得的份数,用平均分的方法解答;二是把比化作分数,转化成分数乘法问题来解答。最后,通过各种形式的练习来巩固这一做法。 3.需破解的问题:对于按比例分配的内容,学生做题正确率很高,但很多都是模仿例题进行做题,真正理解题意的不是很多,这类题容易建构一定的解题模型,在实际的教学中,怎么样杜绝学生照葫芦画瓢似的学习情况的产生呢? 2.使用建议:本教案是按照出示情境图,让学生读图、发现问题、提出问题、明确目标和根据自学指导解决问题的思路进行的,重点在于解决问题的环节,在教学时,教师要给学生一定的思维空间和选择余地,激励学生去发现、去创新 ,体现解决问题策略的多样性。 3.需破解的问题:对于按比例分配的相关内容,容易建构一定的解题模型,在实际的教学中,怎样让学生运用所学的知识,灵活地解决生活中的实际问题,而不是照葫芦画瓢似的学习。 查看更多